第17章 函数及其图象 评估测试卷(含答案)2024-2025学年数学华东师大版八年级下册
文档属性
| 名称 | 第17章 函数及其图象 评估测试卷(含答案)2024-2025学年数学华东师大版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 324.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 00:00:00 | ||
图片预览



文档简介
第17章 函数及其图象评估测试卷
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.在函数y=中,自变量x的取值范围是 ( )
A.x>2 B.x≤2 C.x≥2 D.x≠2
2.若一次函数y=2x+1的图象经过点(-3,y1),(4,y2),则y1与y2的大小关系是 ( )
A.y1y2 C.y1≤y2 D.y1≥y2
3.(2024长沙中考)对于一次函数y=2x-1,下列结论正确的是 ( )
A.它的图象与y轴交于点(0,-1) B.y随x的增大而减小
C.当x>时,y<0 D.它的图象经过第一、二、三象限
4.(2024兴安盟、呼伦贝尔中考)点P(x,y)在直线y=-x+4上,坐标(x,y)是二元一次方程5x-6y=33的解,则点P的位置在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.在平面直角坐标系中,点P在x轴的下方,y轴的右侧,且到x轴的距离为5,到y轴的距离为1,则点P的坐标为 ( )
A.(1,-5) B.(5,1) C.(-1,5) D.(5,-1)
6.(2024大庆中考)在同一平面直角坐标系中,函数y=kx-k(k≠0)与y=的大致图象为 ( )
A B C D
7.(2024广东中考)已知不等式kx+b<0的解集是x<2,则一次函数y=kx+b的图象大致是 ( )
A B C D
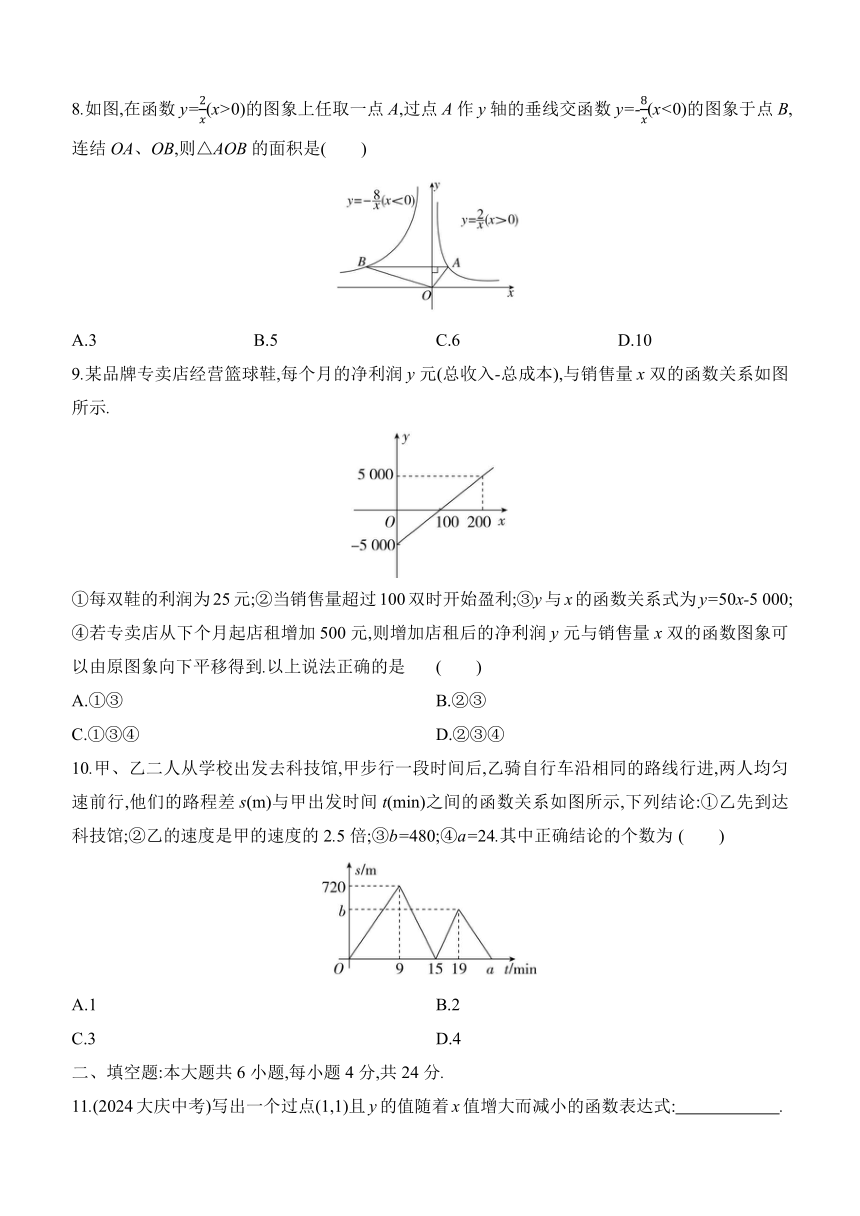
8.如图,在函数y=(x>0)的图象上任取一点A,过点A作y轴的垂线交函数y=-(x<0)的图象于点B,连结OA、OB,则△AOB的面积是( )
A.3 B.5 C.6 D.10
9.某品牌专卖店经营篮球鞋,每个月的净利润y元(总收入-总成本),与销售量x双的函数关系如图所示.
①每双鞋的利润为25元;②当销售量超过100双时开始盈利;③y与x的函数关系式为y=50x-5 000;④若专卖店从下个月起店租增加500元,则增加店租后的净利润y元与销售量x双的函数图象可以由原图象向下平移得到.以上说法正确的是 ( )
A.①③ B.②③
C.①③④ D.②③④
10.甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同的路线行进,两人均匀速前行,他们的路程差s(m)与甲出发时间t(min)之间的函数关系如图所示,下列结论:①乙先到达科技馆;②乙的速度是甲的速度的2.5倍;③b=480;④a=24.其中正确结论的个数为 ( )
A.1 B.2
C.3 D.4
二、填空题:本大题共6小题,每小题4分,共24分.
11.(2024大庆中考)写出一个过点(1,1)且y的值随着x值增大而减小的函数表达式: .
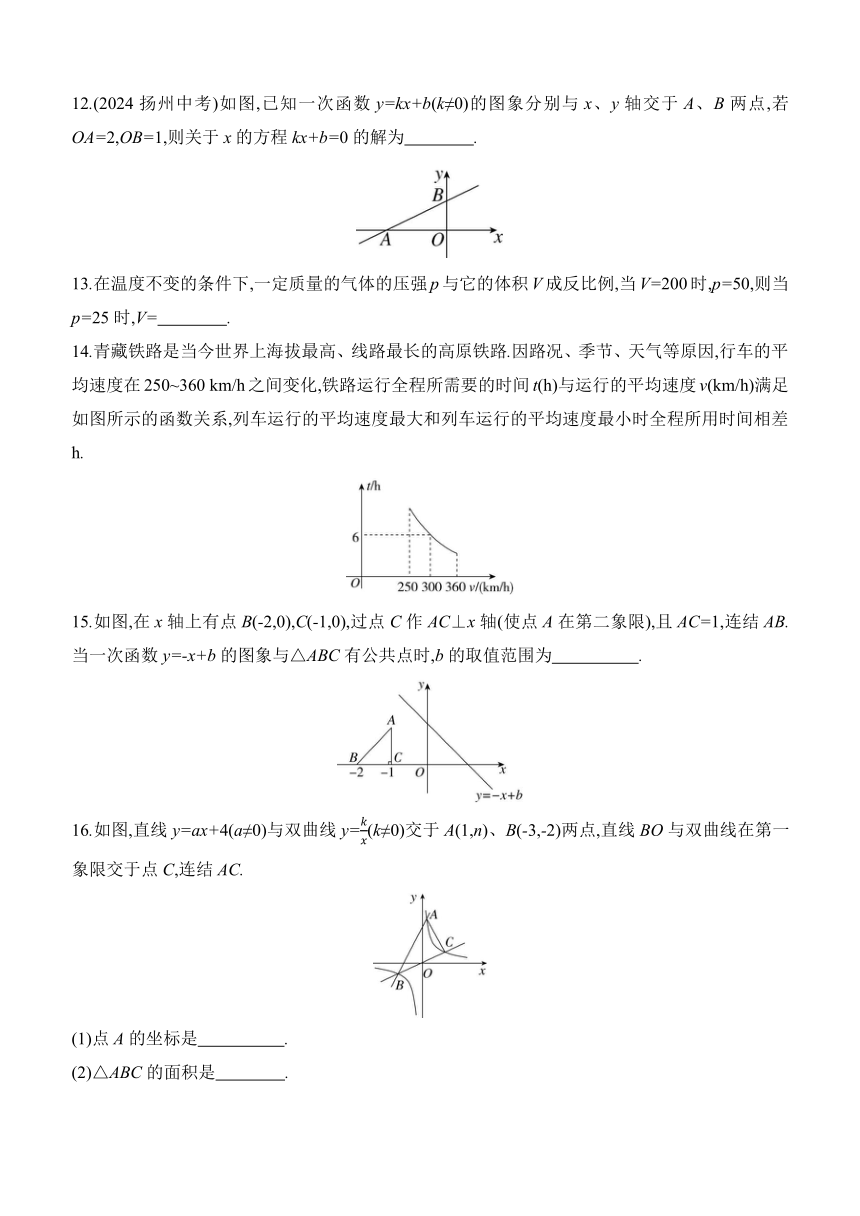
12.(2024扬州中考)如图,已知一次函数y=kx+b(k≠0)的图象分别与x、y轴交于A、B两点,若OA=2,OB=1,则关于x的方程kx+b=0的解为 .
13.在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,p=50,则当p=25时,V= .
14.青藏铁路是当今世界上海拔最高、线路最长的高原铁路.因路况、季节、天气等原因,行车的平均速度在250~360 km/h之间变化,铁路运行全程所需要的时间t(h)与运行的平均速度v(km/h)满足如图所示的函数关系,列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差 h.
15.如图,在x轴上有点B(-2,0),C(-1,0),过点C作AC⊥x轴(使点A在第二象限),且AC=1,连结AB.当一次函数y=-x+b的图象与△ABC有公共点时,b的取值范围为 .
16.如图,直线y=ax+4(a≠0)与双曲线y=(k≠0)交于A(1,n)、B(-3,-2)两点,直线BO与双曲线在第一象限交于点C,连结AC.
(1)点A的坐标是 .
(2)△ABC的面积是 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)一次函数y=kx+b(k≠0)的图象经过点A(3,-2)和点B,其中点B是直线y=2x+1和y=-x+4的交点,求这个一次函数的表达式.
18.(8分)(2024山东四市中考)列表法、表达式法、图象法是三种表示函数的方法,它们从不同角度反映了自变量与函数值之间的对应关系.下表是函数y=2x+b与y=部分自变量与函数值的对应关系:
x - a 1
2x+b a 1
7
(1)求a、b的值,并补全表格.
(2)结合表格,当y=2x+b的图象在y=的图象上方时,直接写出x的取值范围.
19.(8分)在平面直角坐标系中,函数y=kx+b(k≠0)的图象经过点A(0,1)和B(1,2),与过点(0,4)且平行于x轴的直线交于点C.
(1)求该函数的表达式及点C的坐标.
(2)当x<3时,对于x的每一个值,函数 y=x+n的值都大于函数y=kx+b(k≠0)的值且小于4,直接写出n的值.
20.(8分)已知等腰三角形的周长为10 cm,腰长为x cm,底边长为y cm.
(1)以腰长x为自变量,写出y与x之间的函数关系式,并求自变量x的取值范围.
(2)求当y=3时x的值.
(3)画出函数的图象.
21.(8分)科学课上,同学用自制的密度计测量液体的密度,密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度ρ(单位:g/cm3)的反比例函数,当密度计悬浮在密度为1 g/cm3的水中时,h=20 cm.
(1)求h关于ρ的函数关系式.
(2)当密度计悬浮在另一种液体中时,h=25 cm,求该液体的密度ρ.
22.(8分)如图,在平面直角坐标系中,点O是坐标原点,点A(2,5)在反比例函数y=(k≠0)的图象上,过点A的直线y=x+b交x轴于点B.
(1)求k和b的值.
(2)求△OAB的面积.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)(2024甘孜州中考)端午节是我国的传统节日,有吃粽子的习俗.节日前夕,某商场购进A、B两种粽子共200盒进行销售.经了解,进价与标价如下表所示(单位:元/盒):
种类 进价 标价
A 90 120
B 50 60
(1)设该商场购进A种粽子x盒,销售两种粽子所得的总利润为y元,求y关于x的函数关系式(不必写出自变量x的取值范围).
(2)若购进的200盒粽子销售完毕,总利润不低于3 000元,请问至少需要购进A种粽子多少盒
24.(8分)某市荸荠喜获丰收,该市生产基地收获荸荠40 t,经市场调查,可采用批发、零售、加工销售三种销售方式,这三种销售方式每吨荸荠的利润如下表:
销售方式 批发 零售 加工销售
利润/(百元/t) 12 22 30
设按计划全部售出后的总利润为y百元,其中批发量为x t,且加工销售量为15 t.
(1)求y与x之间的函数关系式.
(2)若零售量不超过批发量的4倍,求该生产基地按计划全部售完荸荠后获得的最大利润.
25.(10分)(2024宁夏中考)在同一平面直角坐标系中,函数y=2x+1的图象可以由函数y=2x的图象平移得到.依此想法,数学小组对反比例函数图象的平移进行探究.
【动手操作】
列表:
x … -5 -4 -3 -2 -1 1 2 3 4 5 …
y= … - - - -1 -2 2 1 …
x … -5 -4 -3 -2 - - 0 1 2 3 …
y= … - - -1 -2 -4 4 2 1 …
描点连线:在已画出函数y=的图象的坐标系中画出函数y=的图象.
【探究发现】
(1)将反比例函数y=的图象向 平移 个单位得到函数y=的图象.
(2)上述探究方法运用的数学思想是 .
A.整体思想 B.类比思想 C.分类讨论思想
【应用延伸】
(1)将反比例函数y=-的图象先 ,再 得到函数y=--1的图象.
(2)函数y=--1图象的对称中心的坐标为 .
26.(10分)某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式.
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标.
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
27.(14分)一辆巡逻车从A地出发沿一条笔直的公路匀速驶向B地, h后,一辆货车从A地出发,沿同一路线每小时行驶80 km匀速驶向B地,货车到达B地填装货物耗时15 min,然后立即按原路匀速返回A地.巡逻车、货车离A地的距离y(km)与货车出发时间x(h)之间的函数关系如图所示,请结合图象解答下列问题:
(1)A、B两地之间的距离是 km,a= .
(2)求线段FG所在直线的函数表达式.
(3)货车出发多少小时两车相距15 km (直接写出答案即可)
【详解答案】
1.D 解析:由题意得4-2x≠0,
解得x≠2.
故选D.
2.A 解析:∵一次函数y=2x+1中,k=2>0,
∴y随着x的增大而增大.
∵点(-3,y1)和(4,y2)是一次函数y=2x+1图象上的两个点,-3<4,∴y13.A 解析:A.当x=0时,y=-1,则它的图象与y轴交于点(0,-1),故本选项符合题意;
B.y随x的增大而增大,故本选项不符合题意;
C.当x>时,y>0,故本选项不符合题意;
D.它的图象经过第一、三、四象限,故本选项不符合题意.
故选A.
4.D 解析:解方程组
得
∴P,
∴P在第四象限.
故选D.
5.A 解析:∵点P在x轴的下方,y轴的右侧,∴点P在第四象限,
∵点P到y轴的距离是1,到x轴的距离是5,∴点P的横坐标为1,纵坐标为-5,
∴点P的坐标为(1,-5).故选A.
6.C 解析:将x=1代入y=kx-k得,
y=k-k=0,
所以函数y=kx-k过定点(1,0).
故B选项不符合题意.
当k>0时,
函数y=kx-k中y随x的增大而增大.
因为当k>0时,
y=>0,
所以此函数的图象都在x轴的上方,
所以A、D不符合题意,C符合题意.
故选C.
7.B 解析:A.不等式kx+b<0的解集是x>-2,故本选项不符合题意;
B.不等式kx+b<0的解集是x<2,故本选项符合题意;
C.不等式kx+b<0的解集是x<-2,故本选项不符合题意;
D.不等式kx+b<0的解集是x>2,故本选项不符合题意.
故选B.
8.B 解析:如图.∵点A在函数y=(x>0)的图象上,
∴S△AOC=×2=1.
又∵点B在反比例函数y=-(x<0)的图象上,
∴S△BOC=×8=4.
∴S△AOB=S△AOC+S△BOC=1+4=5.故选B.
9.D 解析:由题图可知,每个月的净利润y元(总收入-总成本)与销售量x双的函数关系是一次函数,设函数关系式为y=kx+b,由题图可知经过点(100,0),(200,5 000),
则
解得
即y与x的函数关系式为y=50x-5 000,故③正确,符合题意;
由题图可知每双的利润为=50(元),故①错误,不符合题意;
当x=100时,y=0,则当销售量超过100双时,开始盈利,故②正确,符合题意,若专卖店从下个月起店租增加500元,则增加店租后的净利润y元与销售量x双的函数关系式为y=50x-5 000-500=50x-5 500,
∴增加店租后的净利润y元与销售量x双的函数图象可以由原图象向下平移500个单位得到的,故④正确,符合题意.
综上可知,说法正确的是②③④.
故选D.
10.C 解析:由题图得出甲步行720 m,需要9 min,∴甲的速度为720÷9=80(m/min).
当第15 min时,乙追上甲,乙走了15-9=6(min),
行进路程为15×80=1 200(m),
∴乙的速度为1 200÷6=200(m/min),
∴200÷80=2.5,故②正确;第19 min以后两人的路程差越来越小,说明乙已经到达终点,则乙先到达科技馆,故①正确;乙到达科技馆时,共走了19-9=10(min),行进路程为10×200=2 000(m),
∴甲到达科技馆用时时间为2 000÷80=25(min),故a的值为25,故④错误;
∵甲19 min行进路程为19×80=1 520(m),
∴b=2 000-1 520=480,故③正确.
故正确的有①②③.故选C.
11.y=-x+2(答案不唯一)
12.x=-2 解析:∵OA=2,
∴一次函数y=kx+b(k≠0)的图象与x轴相交于点A(-2,0),
∴关于x的方程kx+b=0的解为x=-2.
13.400 解析:设p与V的关系式为p=(k≠0),当V=200时,p=50,∴50=,k=10 000.∴p=.当p=25时,V=400.
14.2.2 解析:设反比例函数的表达式为t=,把(300,6)代入t=,得s=300×6=1 800,
∴反比例函数的表达式为t=.
当v=250时,t==7.2(h),
当v=360时,t==5(h),
∴列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差7.2-5=2.2(h).
15.-2≤b≤0 解析:由题意可得,点A的坐标为(-1,1),点B的坐标为(-2,0),
当一次函数y=-x+b的图象经过点A时,1=-(-1)+b,可得b=0;当一次函数y=-x+b的图象经过点B时,0=-(-2)+b,可得b=-2.由上可得,当一次函数y=-x+b的图象与△ABC有公共点时,b的取值范围为-2≤b≤0,
16.(1)(1,6) (2)16 解析:(1)∵点B(-3,-2)在双曲线y=(k≠0)上,
∴k=-3×(-2)=6.
∴y=.∵点A(1,n)在双曲线y=上,
∴n=6.∴A(1,6).
(2)如图,过点B作BG∥x轴,过点C作FG∥y轴,FG和BG交于点G,过点B作BE∥y轴,过点A作AF∥x轴,BE和AF交于点E,FG和AF交于点F.
∵直线BO与双曲线在第一象限交于点C,点B(-3,-2),∴点C的坐标为(3,2).
∵点A(1,6)、B(-3,-2)、C(3,2),∴BE=8,BG=6,CG=4,CF=4,AF=2,AE=4.
∴S△ABC=S长方形BEFG-S△ABE-S△BCG-S△ACF=8×6-×4×8-×6×4-×4×2=48-16-12-4=16.
17.解:由
解得
∴B(1,3).由函数y=kx+b(k≠0)的图象经过点A(3,-2)、B(1,3),得
解得
∴这个一次函数的表达式为y=-x+.
18.解:(1)当x=-时,2x+b=a,即-7+b=a,
当x=a时,2x+b=1,
即2a+b=1,
∴
解得
补全表格如下:
x - a 1
2x+b a 1 7
-2 - 7
(2)-1.
19.解:(1)因为y=kx+b(k≠0)的图象经过点A(0,1)和B(1,2),
所以
解得
所以该函数的表达式为y=x+1.当y=4时,x=3,
所以点C的坐标为(3,4).
(2)n的值为2.
解法提示:因为直线y=x+n与直线y=x平行,
所以将直线y=x+n看作由直线y=x平移所得.
若x=3,×3+n=4,则n=2.
由题意可知当x<3时,y=x+n的值小于4,
所以直线y=x+n在直线x=3左侧的部分都在直线y=4的下方,结合图象可知,可将直线y=x至多向上平移至经过点(3,4)才能满足题意,故n≤2.
已知当x<3时,y=x+n的值大于y=x+1的值,所以直线y=x+n在直线x=3左侧的部分都在直线y=x+1的上方,结合图象可知,应将直线y=x至少向上平移至经过点(3,4)才能满足题意,故n≥2.
综上,n=2.
20.解:(1)∵等腰三角形的周长为10 cm,腰长为x cm,底边长为y cm,
∴2x+y=10,
∴y=10-2x.
∵
解得2.5∴y=10-2x(2.5(2)当y=3时,3=10-2x,
解得x=3.5.
(3)如图所示.
21.解:(1)设h关于ρ的函数关系式为h=(k≠0),
把ρ=1,h=20代入关系式,得k=20,
∴h关于ρ的函数关系式为h=.
(2)把h=25代入h=,得25=.
解得ρ=0.8.
答:该液体的密度ρ为0.8 g/cm3.
22.解:(1)把A(2,5)分别代入y=(k≠0)和y=x+b,
得
解得
(2)如图,过点A作AC⊥于x轴于点C,
由(1)得直线AB的表达式为y=x+3,
∴点B的坐标为(-3,0).
∴OB=3.
∵点A的坐标是(2,5),
∴AC=5.
∴S△OAB=OB·AC=×3×5=.
23.解:(1)y=(120-90)x+(60-50)·(200-x)=20x+2 000,
故y关于x的函数关系式为y=20x+2 000.
(2)20x+2 000≥3 000,
解得x≥50,
故至少需要购进A种粽子50盒.
24.解:(1)依题意可知零售量为(25-x)t,
则y=12x+22(25-x)+30×15,
∴y=-10x+1 000(0≤x≤25).
(2)依题意有
解得5≤x≤25.
∵k=-10<0,
∴y随x的增大而减小,
∴当x=5时,y有最大值,且y最大=950.
故最大利润为950百元.
25.解:【动手操作】
如图所示:
【探究发现】
(1)左 1
(2)B
【应用延伸】
(1)向右平移2个单位 向下平移1个单位
(2)(2,-1)
26.解:(1)由题意可得,银卡消费时,y=10x+150,
普通票消费时,y=20x.
(2)由题意可得,当10x+150=20x时,
解得x=15,则y=300,故点B的坐标为(15,300).
在y=10x+150中,当x=0时,y=150,故点A的坐标为(0,150).
当y=10x+150=600时,解得x=45,故点C的坐标为(45,600).
(3)由A、B、C的坐标可得,当045时,金卡消费更合算.
27.解:(1)60 1
(2)设线段FG所在直线的函数表达式为y=kx+b(k≠0),
将F(1,60),G(2,0)代入y=kx+b,得解得
∴线段FG所在直线的函数表达式为y=-60x+120.
(3)当货车出发 h或 h或 h时,两车相距15 km.
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.在函数y=中,自变量x的取值范围是 ( )
A.x>2 B.x≤2 C.x≥2 D.x≠2
2.若一次函数y=2x+1的图象经过点(-3,y1),(4,y2),则y1与y2的大小关系是 ( )
A.y1
3.(2024长沙中考)对于一次函数y=2x-1,下列结论正确的是 ( )
A.它的图象与y轴交于点(0,-1) B.y随x的增大而减小
C.当x>时,y<0 D.它的图象经过第一、二、三象限
4.(2024兴安盟、呼伦贝尔中考)点P(x,y)在直线y=-x+4上,坐标(x,y)是二元一次方程5x-6y=33的解,则点P的位置在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.在平面直角坐标系中,点P在x轴的下方,y轴的右侧,且到x轴的距离为5,到y轴的距离为1,则点P的坐标为 ( )
A.(1,-5) B.(5,1) C.(-1,5) D.(5,-1)
6.(2024大庆中考)在同一平面直角坐标系中,函数y=kx-k(k≠0)与y=的大致图象为 ( )
A B C D
7.(2024广东中考)已知不等式kx+b<0的解集是x<2,则一次函数y=kx+b的图象大致是 ( )
A B C D
8.如图,在函数y=(x>0)的图象上任取一点A,过点A作y轴的垂线交函数y=-(x<0)的图象于点B,连结OA、OB,则△AOB的面积是( )
A.3 B.5 C.6 D.10
9.某品牌专卖店经营篮球鞋,每个月的净利润y元(总收入-总成本),与销售量x双的函数关系如图所示.
①每双鞋的利润为25元;②当销售量超过100双时开始盈利;③y与x的函数关系式为y=50x-5 000;④若专卖店从下个月起店租增加500元,则增加店租后的净利润y元与销售量x双的函数图象可以由原图象向下平移得到.以上说法正确的是 ( )
A.①③ B.②③
C.①③④ D.②③④
10.甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同的路线行进,两人均匀速前行,他们的路程差s(m)与甲出发时间t(min)之间的函数关系如图所示,下列结论:①乙先到达科技馆;②乙的速度是甲的速度的2.5倍;③b=480;④a=24.其中正确结论的个数为 ( )
A.1 B.2
C.3 D.4
二、填空题:本大题共6小题,每小题4分,共24分.
11.(2024大庆中考)写出一个过点(1,1)且y的值随着x值增大而减小的函数表达式: .
12.(2024扬州中考)如图,已知一次函数y=kx+b(k≠0)的图象分别与x、y轴交于A、B两点,若OA=2,OB=1,则关于x的方程kx+b=0的解为 .
13.在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,p=50,则当p=25时,V= .
14.青藏铁路是当今世界上海拔最高、线路最长的高原铁路.因路况、季节、天气等原因,行车的平均速度在250~360 km/h之间变化,铁路运行全程所需要的时间t(h)与运行的平均速度v(km/h)满足如图所示的函数关系,列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差 h.
15.如图,在x轴上有点B(-2,0),C(-1,0),过点C作AC⊥x轴(使点A在第二象限),且AC=1,连结AB.当一次函数y=-x+b的图象与△ABC有公共点时,b的取值范围为 .
16.如图,直线y=ax+4(a≠0)与双曲线y=(k≠0)交于A(1,n)、B(-3,-2)两点,直线BO与双曲线在第一象限交于点C,连结AC.
(1)点A的坐标是 .
(2)△ABC的面积是 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)一次函数y=kx+b(k≠0)的图象经过点A(3,-2)和点B,其中点B是直线y=2x+1和y=-x+4的交点,求这个一次函数的表达式.
18.(8分)(2024山东四市中考)列表法、表达式法、图象法是三种表示函数的方法,它们从不同角度反映了自变量与函数值之间的对应关系.下表是函数y=2x+b与y=部分自变量与函数值的对应关系:
x - a 1
2x+b a 1
7
(1)求a、b的值,并补全表格.
(2)结合表格,当y=2x+b的图象在y=的图象上方时,直接写出x的取值范围.
19.(8分)在平面直角坐标系中,函数y=kx+b(k≠0)的图象经过点A(0,1)和B(1,2),与过点(0,4)且平行于x轴的直线交于点C.
(1)求该函数的表达式及点C的坐标.
(2)当x<3时,对于x的每一个值,函数 y=x+n的值都大于函数y=kx+b(k≠0)的值且小于4,直接写出n的值.
20.(8分)已知等腰三角形的周长为10 cm,腰长为x cm,底边长为y cm.
(1)以腰长x为自变量,写出y与x之间的函数关系式,并求自变量x的取值范围.
(2)求当y=3时x的值.
(3)画出函数的图象.
21.(8分)科学课上,同学用自制的密度计测量液体的密度,密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度ρ(单位:g/cm3)的反比例函数,当密度计悬浮在密度为1 g/cm3的水中时,h=20 cm.
(1)求h关于ρ的函数关系式.
(2)当密度计悬浮在另一种液体中时,h=25 cm,求该液体的密度ρ.
22.(8分)如图,在平面直角坐标系中,点O是坐标原点,点A(2,5)在反比例函数y=(k≠0)的图象上,过点A的直线y=x+b交x轴于点B.
(1)求k和b的值.
(2)求△OAB的面积.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)(2024甘孜州中考)端午节是我国的传统节日,有吃粽子的习俗.节日前夕,某商场购进A、B两种粽子共200盒进行销售.经了解,进价与标价如下表所示(单位:元/盒):
种类 进价 标价
A 90 120
B 50 60
(1)设该商场购进A种粽子x盒,销售两种粽子所得的总利润为y元,求y关于x的函数关系式(不必写出自变量x的取值范围).
(2)若购进的200盒粽子销售完毕,总利润不低于3 000元,请问至少需要购进A种粽子多少盒
24.(8分)某市荸荠喜获丰收,该市生产基地收获荸荠40 t,经市场调查,可采用批发、零售、加工销售三种销售方式,这三种销售方式每吨荸荠的利润如下表:
销售方式 批发 零售 加工销售
利润/(百元/t) 12 22 30
设按计划全部售出后的总利润为y百元,其中批发量为x t,且加工销售量为15 t.
(1)求y与x之间的函数关系式.
(2)若零售量不超过批发量的4倍,求该生产基地按计划全部售完荸荠后获得的最大利润.
25.(10分)(2024宁夏中考)在同一平面直角坐标系中,函数y=2x+1的图象可以由函数y=2x的图象平移得到.依此想法,数学小组对反比例函数图象的平移进行探究.
【动手操作】
列表:
x … -5 -4 -3 -2 -1 1 2 3 4 5 …
y= … - - - -1 -2 2 1 …
x … -5 -4 -3 -2 - - 0 1 2 3 …
y= … - - -1 -2 -4 4 2 1 …
描点连线:在已画出函数y=的图象的坐标系中画出函数y=的图象.
【探究发现】
(1)将反比例函数y=的图象向 平移 个单位得到函数y=的图象.
(2)上述探究方法运用的数学思想是 .
A.整体思想 B.类比思想 C.分类讨论思想
【应用延伸】
(1)将反比例函数y=-的图象先 ,再 得到函数y=--1的图象.
(2)函数y=--1图象的对称中心的坐标为 .
26.(10分)某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式.
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标.
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
27.(14分)一辆巡逻车从A地出发沿一条笔直的公路匀速驶向B地, h后,一辆货车从A地出发,沿同一路线每小时行驶80 km匀速驶向B地,货车到达B地填装货物耗时15 min,然后立即按原路匀速返回A地.巡逻车、货车离A地的距离y(km)与货车出发时间x(h)之间的函数关系如图所示,请结合图象解答下列问题:
(1)A、B两地之间的距离是 km,a= .
(2)求线段FG所在直线的函数表达式.
(3)货车出发多少小时两车相距15 km (直接写出答案即可)
【详解答案】
1.D 解析:由题意得4-2x≠0,
解得x≠2.
故选D.
2.A 解析:∵一次函数y=2x+1中,k=2>0,
∴y随着x的增大而增大.
∵点(-3,y1)和(4,y2)是一次函数y=2x+1图象上的两个点,-3<4,∴y1
B.y随x的增大而增大,故本选项不符合题意;
C.当x>时,y>0,故本选项不符合题意;
D.它的图象经过第一、三、四象限,故本选项不符合题意.
故选A.
4.D 解析:解方程组
得
∴P,
∴P在第四象限.
故选D.
5.A 解析:∵点P在x轴的下方,y轴的右侧,∴点P在第四象限,
∵点P到y轴的距离是1,到x轴的距离是5,∴点P的横坐标为1,纵坐标为-5,
∴点P的坐标为(1,-5).故选A.
6.C 解析:将x=1代入y=kx-k得,
y=k-k=0,
所以函数y=kx-k过定点(1,0).
故B选项不符合题意.
当k>0时,
函数y=kx-k中y随x的增大而增大.
因为当k>0时,
y=>0,
所以此函数的图象都在x轴的上方,
所以A、D不符合题意,C符合题意.
故选C.
7.B 解析:A.不等式kx+b<0的解集是x>-2,故本选项不符合题意;
B.不等式kx+b<0的解集是x<2,故本选项符合题意;
C.不等式kx+b<0的解集是x<-2,故本选项不符合题意;
D.不等式kx+b<0的解集是x>2,故本选项不符合题意.
故选B.
8.B 解析:如图.∵点A在函数y=(x>0)的图象上,
∴S△AOC=×2=1.
又∵点B在反比例函数y=-(x<0)的图象上,
∴S△BOC=×8=4.
∴S△AOB=S△AOC+S△BOC=1+4=5.故选B.
9.D 解析:由题图可知,每个月的净利润y元(总收入-总成本)与销售量x双的函数关系是一次函数,设函数关系式为y=kx+b,由题图可知经过点(100,0),(200,5 000),
则
解得
即y与x的函数关系式为y=50x-5 000,故③正确,符合题意;
由题图可知每双的利润为=50(元),故①错误,不符合题意;
当x=100时,y=0,则当销售量超过100双时,开始盈利,故②正确,符合题意,若专卖店从下个月起店租增加500元,则增加店租后的净利润y元与销售量x双的函数关系式为y=50x-5 000-500=50x-5 500,
∴增加店租后的净利润y元与销售量x双的函数图象可以由原图象向下平移500个单位得到的,故④正确,符合题意.
综上可知,说法正确的是②③④.
故选D.
10.C 解析:由题图得出甲步行720 m,需要9 min,∴甲的速度为720÷9=80(m/min).
当第15 min时,乙追上甲,乙走了15-9=6(min),
行进路程为15×80=1 200(m),
∴乙的速度为1 200÷6=200(m/min),
∴200÷80=2.5,故②正确;第19 min以后两人的路程差越来越小,说明乙已经到达终点,则乙先到达科技馆,故①正确;乙到达科技馆时,共走了19-9=10(min),行进路程为10×200=2 000(m),
∴甲到达科技馆用时时间为2 000÷80=25(min),故a的值为25,故④错误;
∵甲19 min行进路程为19×80=1 520(m),
∴b=2 000-1 520=480,故③正确.
故正确的有①②③.故选C.
11.y=-x+2(答案不唯一)
12.x=-2 解析:∵OA=2,
∴一次函数y=kx+b(k≠0)的图象与x轴相交于点A(-2,0),
∴关于x的方程kx+b=0的解为x=-2.
13.400 解析:设p与V的关系式为p=(k≠0),当V=200时,p=50,∴50=,k=10 000.∴p=.当p=25时,V=400.
14.2.2 解析:设反比例函数的表达式为t=,把(300,6)代入t=,得s=300×6=1 800,
∴反比例函数的表达式为t=.
当v=250时,t==7.2(h),
当v=360时,t==5(h),
∴列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差7.2-5=2.2(h).
15.-2≤b≤0 解析:由题意可得,点A的坐标为(-1,1),点B的坐标为(-2,0),
当一次函数y=-x+b的图象经过点A时,1=-(-1)+b,可得b=0;当一次函数y=-x+b的图象经过点B时,0=-(-2)+b,可得b=-2.由上可得,当一次函数y=-x+b的图象与△ABC有公共点时,b的取值范围为-2≤b≤0,
16.(1)(1,6) (2)16 解析:(1)∵点B(-3,-2)在双曲线y=(k≠0)上,
∴k=-3×(-2)=6.
∴y=.∵点A(1,n)在双曲线y=上,
∴n=6.∴A(1,6).
(2)如图,过点B作BG∥x轴,过点C作FG∥y轴,FG和BG交于点G,过点B作BE∥y轴,过点A作AF∥x轴,BE和AF交于点E,FG和AF交于点F.
∵直线BO与双曲线在第一象限交于点C,点B(-3,-2),∴点C的坐标为(3,2).
∵点A(1,6)、B(-3,-2)、C(3,2),∴BE=8,BG=6,CG=4,CF=4,AF=2,AE=4.
∴S△ABC=S长方形BEFG-S△ABE-S△BCG-S△ACF=8×6-×4×8-×6×4-×4×2=48-16-12-4=16.
17.解:由
解得
∴B(1,3).由函数y=kx+b(k≠0)的图象经过点A(3,-2)、B(1,3),得
解得
∴这个一次函数的表达式为y=-x+.
18.解:(1)当x=-时,2x+b=a,即-7+b=a,
当x=a时,2x+b=1,
即2a+b=1,
∴
解得
补全表格如下:
x - a 1
2x+b a 1 7
-2 - 7
(2)-
19.解:(1)因为y=kx+b(k≠0)的图象经过点A(0,1)和B(1,2),
所以
解得
所以该函数的表达式为y=x+1.当y=4时,x=3,
所以点C的坐标为(3,4).
(2)n的值为2.
解法提示:因为直线y=x+n与直线y=x平行,
所以将直线y=x+n看作由直线y=x平移所得.
若x=3,×3+n=4,则n=2.
由题意可知当x<3时,y=x+n的值小于4,
所以直线y=x+n在直线x=3左侧的部分都在直线y=4的下方,结合图象可知,可将直线y=x至多向上平移至经过点(3,4)才能满足题意,故n≤2.
已知当x<3时,y=x+n的值大于y=x+1的值,所以直线y=x+n在直线x=3左侧的部分都在直线y=x+1的上方,结合图象可知,应将直线y=x至少向上平移至经过点(3,4)才能满足题意,故n≥2.
综上,n=2.
20.解:(1)∵等腰三角形的周长为10 cm,腰长为x cm,底边长为y cm,
∴2x+y=10,
∴y=10-2x.
∵
解得2.5
解得x=3.5.
(3)如图所示.
21.解:(1)设h关于ρ的函数关系式为h=(k≠0),
把ρ=1,h=20代入关系式,得k=20,
∴h关于ρ的函数关系式为h=.
(2)把h=25代入h=,得25=.
解得ρ=0.8.
答:该液体的密度ρ为0.8 g/cm3.
22.解:(1)把A(2,5)分别代入y=(k≠0)和y=x+b,
得
解得
(2)如图,过点A作AC⊥于x轴于点C,
由(1)得直线AB的表达式为y=x+3,
∴点B的坐标为(-3,0).
∴OB=3.
∵点A的坐标是(2,5),
∴AC=5.
∴S△OAB=OB·AC=×3×5=.
23.解:(1)y=(120-90)x+(60-50)·(200-x)=20x+2 000,
故y关于x的函数关系式为y=20x+2 000.
(2)20x+2 000≥3 000,
解得x≥50,
故至少需要购进A种粽子50盒.
24.解:(1)依题意可知零售量为(25-x)t,
则y=12x+22(25-x)+30×15,
∴y=-10x+1 000(0≤x≤25).
(2)依题意有
解得5≤x≤25.
∵k=-10<0,
∴y随x的增大而减小,
∴当x=5时,y有最大值,且y最大=950.
故最大利润为950百元.
25.解:【动手操作】
如图所示:
【探究发现】
(1)左 1
(2)B
【应用延伸】
(1)向右平移2个单位 向下平移1个单位
(2)(2,-1)
26.解:(1)由题意可得,银卡消费时,y=10x+150,
普通票消费时,y=20x.
(2)由题意可得,当10x+150=20x时,
解得x=15,则y=300,故点B的坐标为(15,300).
在y=10x+150中,当x=0时,y=150,故点A的坐标为(0,150).
当y=10x+150=600时,解得x=45,故点C的坐标为(45,600).
(3)由A、B、C的坐标可得,当0
27.解:(1)60 1
(2)设线段FG所在直线的函数表达式为y=kx+b(k≠0),
将F(1,60),G(2,0)代入y=kx+b,得解得
∴线段FG所在直线的函数表达式为y=-60x+120.
(3)当货车出发 h或 h或 h时,两车相距15 km.
