第18章 平行四边形 评估测试卷(含答案)2024-2025学年数学华东师大版八年级下册
文档属性
| 名称 | 第18章 平行四边形 评估测试卷(含答案)2024-2025学年数学华东师大版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 312.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 00:00:00 | ||
图片预览



文档简介
第18章 平行四边形 评估测试卷
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.如图,在平行四边形ABCD中,点O为对角线AC、BD的交点,与△AOD全等的是 ( )
A.△ABC B.△ADC C.△BCD D.△COB
2.已知 ABCD的周长为32,AB=4,则BC的长为 ( )
A.4 B.12 C.24 D.28
3.平行四边形的一边长为10 cm,那么这个平行四边形的两条对角线的长可以是 ( )
A.4 cm和6 cm B.10 cm和12 cm C.8 cm和10 cm D.6 cm和8 cm
4.如图,平行四边形ABCD中,AE平分∠DAB,∠B=100°,则∠DEA等于 ( )
A.100° B.80° C.60° D.40°
5.如图,四边形ABCD是平行四边形,对角线AC与BD交于点O,若AC=2AB,∠BAO=94°,则∠AOD的度数为 ( )
A.157° B.147° C.137° D.127°
6.已知四边形ABCD,对角线AC与BD交于点O,从下列条件中:①AB∥CD;②AD=BC;③∠ABC=∠ADC;④OA=OC,任取其中两个,以下组合能够判定四边形ABCD是平行四边形的是( )
A.①② B.②③ C.②④ D.①④
7.如图,在 ABCD中,AB=8,点E是AB上一点,AE=3,连结DE,过点C作CF∥DE,交AB的延长线于点F,则BF的长为( )
A.5 B.4 C.3 D.2
8.如图,点E、F分别是 ABCD的边AD、BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到四边形EFC'D',ED'交BC于点G,则△GEF的周长为 ( )
A.6 B.12
C.18 D.24
9.如图1, ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N、M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案是 ( )
A.甲、乙、丙 B.只有甲、乙
C.只有甲、丙 D.只有乙、丙
10.(2024眉山中考)如图,在 ABCD中,点O是BD的中点,EF过点O,下列结论:①AB∥DC;②EO=ED;③∠A=∠C;④S四边形ABOE=S四边形CDOF,其中正确结论的个数为 ( )
A.1 B.2
C.3 D.4
二、填空题:本大题共6小题,每小题4分,共24分.
11.在四边形ABCD中,∠A=∠C,要使四边形 ABCD 为平行四边形,则应添加的条件是
(添加一个条件即可).
12.平行四边形相邻两边长之比为3∶5,它的周长为32 cm,则这个平行四边形较长的边长为
cm.
13.在 ABCD中,∠A+∠C=100°,则∠B= °.
14.如图,将 ABCD折叠,使顶点D恰好落在AB边上的点M处,折痕为AN,那么对于结论:①MN∥BC,②MN=AM,说法正确的是 (将正确结论的序号填在横线上).
15.如图,在平行四边形ABCD中,按以下步骤作图:①以点A为圆心,任意长为半径作弧,分别交AB、AD于点M、N;②分别以点M、N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线AP,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD的周长为 .
16.(2024广安中考)如图,在 ABCD中,AB=4,AD=5,∠ABC=30°,点M为直线BC上一动点,则MA+MD的最小值为 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(7分)(2024泸州中考)如图,在 ABCD中,E、F是对角线BD上的点,且DE=BF.
求证:∠1=∠2.
18.(7分)如图,在 ABCD中,E是BC边上一点,连结AE、AC、ED,AE=AB.
求证:AC=DE.
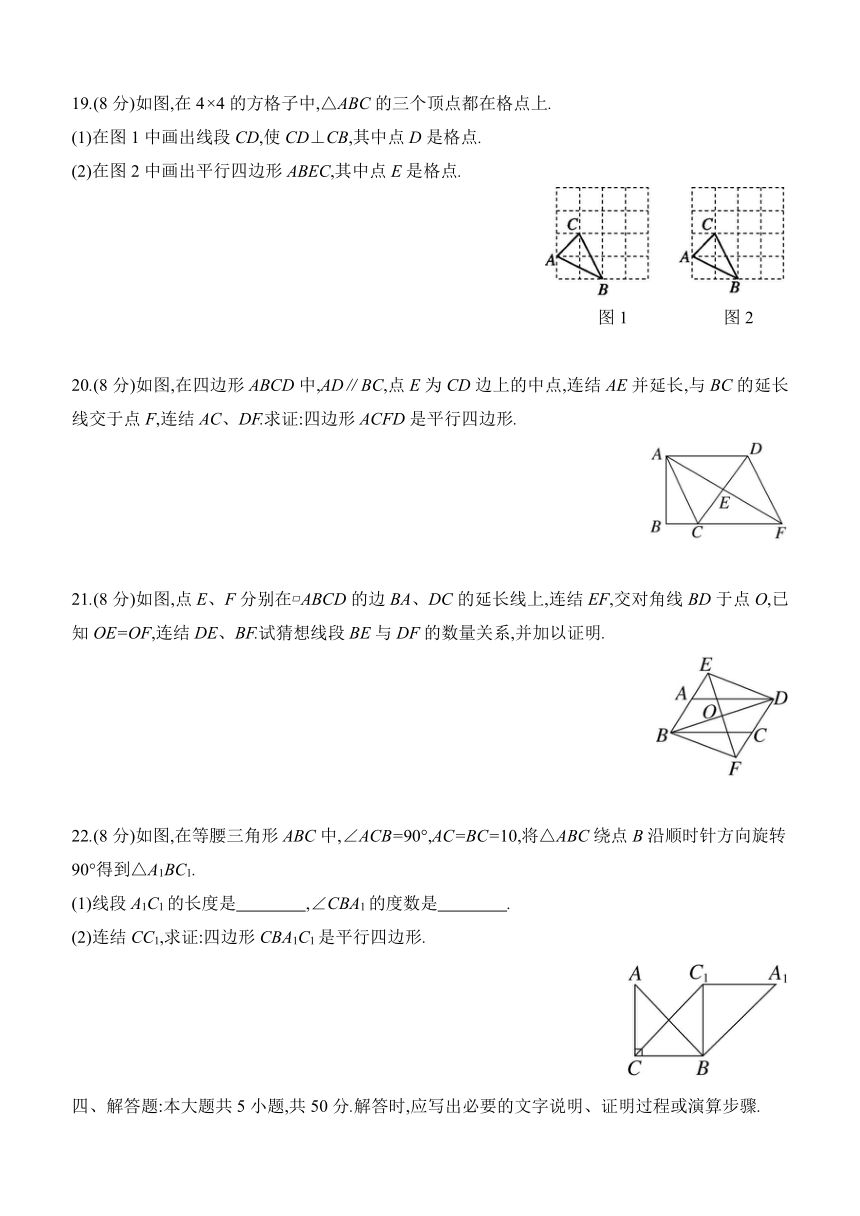
19.(8分)如图,在4×4的方格子中,△ABC的三个顶点都在格点上.
(1)在图1中画出线段CD,使CD⊥CB,其中点D是格点.
(2)在图2中画出平行四边形ABEC,其中点E是格点.
图1 图2
20.(8分)如图,在四边形ABCD中,AD∥BC,点E为CD边上的中点,连结AE并延长,与BC的延长线交于点F,连结AC、DF.求证:四边形ACFD是平行四边形.
21.(8分)如图,点E、F分别在 ABCD的边BA、DC的延长线上,连结EF,交对角线BD于点O,已知OE=OF,连结DE、BF.试猜想线段BE与DF的数量关系,并加以证明.
22.(8分)如图,在等腰三角形ABC中,∠ACB=90°,AC=BC=10,将△ABC绕点B沿顺时针方向旋转90°得到△A1BC1.
(1)线段A1C1的长度是 ,∠CBA1的度数是 .
(2)连结CC1,求证:四边形CBA1C1是平行四边形.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
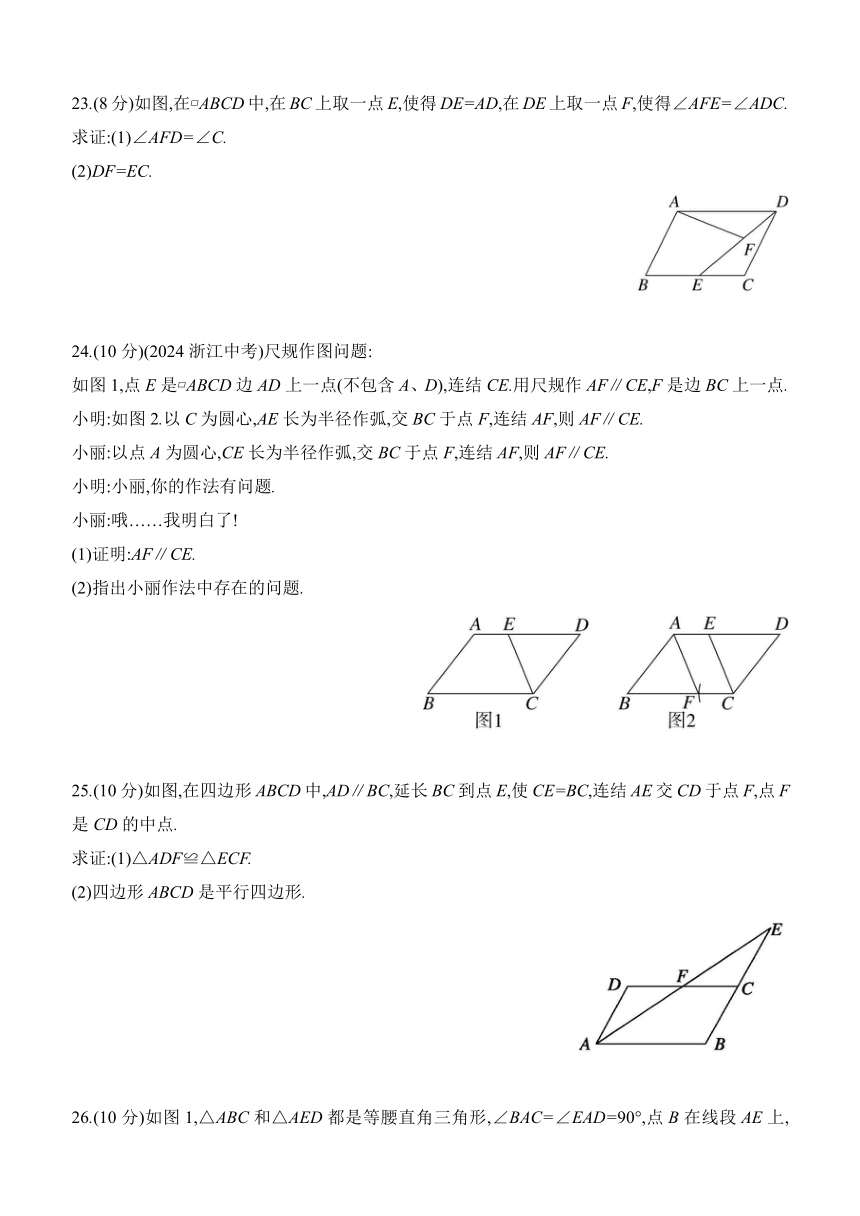
23.(8分)如图,在 ABCD中,在BC上取一点E,使得DE=AD,在DE上取一点F,使得∠AFE=∠ADC.
求证:(1)∠AFD=∠C.
(2)DF=EC.
24.(10分)(2024浙江中考)尺规作图问题:
如图1,点E是 ABCD边AD上一点(不包含A、D),连结CE.用尺规作AF∥CE,F是边BC上一点.
小明:如图2.以C为圆心,AE长为半径作弧,交BC于点F,连结AF,则AF∥CE.
小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连结AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦……我明白了!
(1)证明:AF∥CE.
(2)指出小丽作法中存在的问题.
25.(10分)如图,在四边形ABCD中,AD∥BC,延长BC到点E,使CE=BC,连结AE交CD于点F,点F是CD的中点.
求证:(1)△ADF≌△ECF.
(2)四边形ABCD是平行四边形.
26.(10分)如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
(1)线段BE与线段CD的数量关系: .
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0°<α<360°).
①(1)中的结论是否成立 若成立,请利用图2证明;若不成立,请说明理由.
②当AC=ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形 若存在,请直接写出角α的度数;若不存在,请说明理由.
27.(12分)如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧点P从点A出发沿射线AD以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连结 PE,设点P的运动时间为t s.
(1)若PE⊥BC,求BQ的长.
(2)请问是否存在t的值,使以A、B、E、P为顶点的四边形为平行四边形 若存在,求出t的值,若不存在,请说明理由.
【详解答案】
1.D 解析:由题意可知OA=OC,∠AOD=∠COB,OD=OB,
∴△AOD≌△COB.故选D.
2.B
3.B 解析:平行四边形的对角线各自的一半与已知边组成三角形,利用三角形的三边关系可以得出结论.故选B.
4.D 解析:∵四边形ABCD是平行四边形,∠B=100°,∴∠D=∠B=100°,∵AB∥CD,∴∠DEA=∠EAB,∵AE平分∠DAB,∴∠DAE=∠EAB,∴∠DAE=∠DEA,
∴∠DEA=(180°-∠D)=40°,故选D.
5.C 解析:∵四边形ABCD是平行四边形,∴OA=OC,即AC=2OA,∵AC=2AB,∴AB=OA,∴∠ABO=∠AOB=(180°-∠BAO)=43°,∴∠AOD=∠ABO+∠BAO=43°+94°=137°.故选C.
6.D 解析:以①④作为条件,能够判定四边形ABCD是平行四边形.理由:∵AB∥CD,∴∠OAB=∠OCD.在△AOB和△COD中,∠OAB=∠OCD, AO=CO,∠AOB=∠COD,∴△AOB≌△COD(A.S.A.),∴OB=OD,∴四边形ABCD是平行四边形.故选D.
7.C 解析:在 ABCD中,AB=8,
∴CD=AB=8,AB∥CD.
∵AE=3,∴BE=AB-AE=5.
∵CF∥DE,∴四边形DEFC是平行四边形.
∴CD=EF=8.∴BF=EF-BE=8-5=3.故选C.
8.C 解析:由折叠的性质可知,∠GEF=∠DEF=60°.∵AD∥BC,∴∠GFE=∠DEF=60°.∴△GEF是等边三角形.又∵EF=6,∴△GEF的周长为18.故选C.
9.A 解析:方案甲中,连结AC,如图所示:
∵四边形ABCD是平行四边形,点O为BD的中点,
∴OB=OD,OA=OC,
∵BN=NO,OM=MD,
∴NO=OM,
∴四边形ANCM为平行四边形,方案甲正确;
方案乙中,∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABN=∠CDM,
∵AN⊥BD,CM⊥BD,
∴∠ANB=∠CMD=90°,
∴AN∥CM,在△ABN和△CDM中,
∴△ABN≌△CDM.∴AN=CM,
又∵AN∥CM,
∴四边形ANCM为平行四边形,方案乙正确;
方案丙中,∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,AB=CD,AB∥CD,
∴∠ABN=∠CDM,
∵AN平分∠BAD,CM平分∠BCD,
∴∠BAN=∠DCM,
在△ABN和△CDM中,
∴△ABN≌△CDM(A.S.A.),
∴AN=CM,∠ANB=∠CMD,
∴∠ANM=∠CMN,∴AN∥CM,
∴四边形ANCM为平行四边形,方案丙正确.故选A.
10.C 解析:∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,∠A=∠C,故①③正确;
∴S△ABD=S△CDB=S ABCD,∠ODE=∠OBF,
∵点O是BD的中点,∴OD=OB,
又∵∠DOE=∠BOF,∴△ODE≌△OBF(A.S.A.),
∴S△ODE=S△OBF,EO=FO≠ED,故②不正确;
∵S△ABD=S△CDB,S△ODE=S△OBF,
∴S△ABD-S△ODE=S△CDB-S△OBF,
即S四边形ABOE=S四边形CDOF,故④正确.
综上所述,正确结论的个数为3,
故选C.
11.∠B=∠D(答案不唯一)
12.10 解析:∵平行四边形的周长为32 cm,∴邻边和为16 cm.又∵相邻两边之比为3∶5,则这个平行四边形较长的边长为10 cm.
13.130 解析:如图,在 ABCD中,∠A+∠C=100°,∠A=∠C,AB∥CD,∴∠A=∠C=50°,∠C+∠B=180°,∴∠B=180°-∠C=130°.
14.①② 解析:首先由折叠知MN=DN,∠AND=∠ANM,再由平行四边形的性质知∠AND=∠NAM,所以∠NAM=∠ANM,因此AM=MN,所以结论②是正确的.又因为∠DAN=∠MAN,所以∠DAN=∠ANM,所以AD∥MN,因为AD∥BC,所以MN∥BC,所以结论①是正确的.
15.15 解析:由题意可知,AQ是∠BAD的平分线,∴∠DAQ=∠BAQ.∵四边形ABCD是平行四边形,∴AB∥CD.∴∠DQA=∠BAQ.∴∠DQA=∠DAQ.∴DQ=DA=BC=3.∵DQ=2QC,∴QC=1.5,∴CD=3+1.5=4.5.∴平行四边形ABCD的周长为2(BC+CD)=2×(3+4.5)=2×7.5=15.
16. 解析:如图,作点A关于直线BC的对称点A',连结A'D交BC于点M',则AH=A'H,AH⊥BC,AM'=A'M',
∴当M,M'重合时,MA+MD最小,最小值为A'D,
∵AB=4,∠ABC=30°,
∴A'B=4,∠A'BC=30°,
∴∠ABA'=60°,△ABA'是等边三角形,
∴AA'=AB=4,∵AA'⊥BC,BC∥AD,∴AA'⊥AD,
∵AD=5,
∴A'D==.
17.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADE=∠CBF.
在△ADE和△CBF中,
∴△ADE≌△CBF(S.A.S.),
∴∠1=∠2.
18.证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠DAE=∠AEB.
∵AB=AE,∴∠AEB=∠B.
∴∠B=∠DAE.
在△ABC和△EAD中,
∴△ABC≌△EAD(S.A.S.).
∴AC=DE.
19.解:(1)如图1,线段CD就是所求作的图形.
图1
(2)如图2,平行四边形ABEC就是所求作的图形.
图2
20.证明:∵AD∥BC,
∴∠ADE=∠FCE.
∵E为CD的中点,∴CE=DE,
在△ADE和△FCE中,
∠ADE=∠FCE, DE=CE,
∠AED=∠FEC,
∴△ADE≌△FCE(A.S.A.),
∴AE=FE,
∵DE=CE,
∴四边形ACFD是平行四边形.
21.解:BE=DF.
证明如下:
在 ABCD中,BE∥ FD,则
∠EBO=∠FDO.
在△BOE与△DOF 中,
∴△BOE≌△DOF(A.A.S.),
∴BE=DF.
22.解:(1)10 135°
(2)证明:∵∠A1C1B=∠C1BC=90°,∴A1C1∥BC.
又∵A1C1=AC=BC,
∴四边形CBA1C1是平行四边形.
23.证明:(1)四边形ABCD是平行四边形,∴AD∥BC,
∴∠C+∠ADC=180°.
∵∠AFD+∠AFE=180°,
∠AFE=∠ADC,
∴∠AFD=∠C.
(2)∵AD∥BC,∴∠ADF=∠DEC.
在△AFD和△DCE中,
∵∠ADF=∠DEC,∠AFD=∠C,AD=DE,
∴△AFD≌△DCE(A.A.S.),
∴DF=EC.
24.解:(1)证明:根据小明的作法知,CF=AE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵CF=AE,
∴四边形AFCE是平行四边形,
∴AF∥CE.
(2)以A为圆心,EC为半径画弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.
故小丽的作法有问题.
25.证明:(1)∵AD∥BC,
∴∠DAF=∠E.
∵点F是CD的中点,∴DF=CF.
在△ADF与△ECF中,
∴△ADF≌△ECF(A.A.S.).
(2)∵△ADF≌△ECF,∴AD=EC.
∵CE=BC,∴AD=BC.
∵AD∥BC,∴四边形ABCD是平行四边形.
26.解:(1)BE=CD
(2)①成立.
证明:∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD.
由旋转得∠BAE=∠CAD,
∴△BAE≌△CAD(S.A.S.).∴BE=CD.
②存在,角α的度数是45°或225°或315°.
27.解:(1)过点A作AM⊥BC于点M,设PE交AC于点N.如图所示,
∵∠BAC=90°,∠B=45°,
∴AB=AC,
∵AM⊥BC,
∴BM=CM,∠BAM=∠CAM=45°=∠B=∠C,
∴AM=BM=CM=BC=5,
∵AD∥BC,∴∠PAN=∠C=45°,
∵PE⊥BC,
∴PE=AM=5,PE⊥AD,
∴△APN和△CEN是等腰直角三角形,
∴PN=AP=t,CE=NE=5-t,
∵CE=CQ-QE=2t-2,
∴5-t=2t-2,解得t=,
∴BQ=BC-CQ=10-2×=.
(2)存在.
若以A、B、E、P为顶点的四边形为平行四边形,
则AP=BE,
∴t=10-2t+2 或t=2t-2-10,
解得t=4或12,
∴存在t的值,使以A、B、E、P为顶点的四边形为平行四边形,此时t=4或12.
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.如图,在平行四边形ABCD中,点O为对角线AC、BD的交点,与△AOD全等的是 ( )
A.△ABC B.△ADC C.△BCD D.△COB
2.已知 ABCD的周长为32,AB=4,则BC的长为 ( )
A.4 B.12 C.24 D.28
3.平行四边形的一边长为10 cm,那么这个平行四边形的两条对角线的长可以是 ( )
A.4 cm和6 cm B.10 cm和12 cm C.8 cm和10 cm D.6 cm和8 cm
4.如图,平行四边形ABCD中,AE平分∠DAB,∠B=100°,则∠DEA等于 ( )
A.100° B.80° C.60° D.40°
5.如图,四边形ABCD是平行四边形,对角线AC与BD交于点O,若AC=2AB,∠BAO=94°,则∠AOD的度数为 ( )
A.157° B.147° C.137° D.127°
6.已知四边形ABCD,对角线AC与BD交于点O,从下列条件中:①AB∥CD;②AD=BC;③∠ABC=∠ADC;④OA=OC,任取其中两个,以下组合能够判定四边形ABCD是平行四边形的是( )
A.①② B.②③ C.②④ D.①④
7.如图,在 ABCD中,AB=8,点E是AB上一点,AE=3,连结DE,过点C作CF∥DE,交AB的延长线于点F,则BF的长为( )
A.5 B.4 C.3 D.2
8.如图,点E、F分别是 ABCD的边AD、BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到四边形EFC'D',ED'交BC于点G,则△GEF的周长为 ( )
A.6 B.12
C.18 D.24
9.如图1, ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N、M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案是 ( )
A.甲、乙、丙 B.只有甲、乙
C.只有甲、丙 D.只有乙、丙
10.(2024眉山中考)如图,在 ABCD中,点O是BD的中点,EF过点O,下列结论:①AB∥DC;②EO=ED;③∠A=∠C;④S四边形ABOE=S四边形CDOF,其中正确结论的个数为 ( )
A.1 B.2
C.3 D.4
二、填空题:本大题共6小题,每小题4分,共24分.
11.在四边形ABCD中,∠A=∠C,要使四边形 ABCD 为平行四边形,则应添加的条件是
(添加一个条件即可).
12.平行四边形相邻两边长之比为3∶5,它的周长为32 cm,则这个平行四边形较长的边长为
cm.
13.在 ABCD中,∠A+∠C=100°,则∠B= °.
14.如图,将 ABCD折叠,使顶点D恰好落在AB边上的点M处,折痕为AN,那么对于结论:①MN∥BC,②MN=AM,说法正确的是 (将正确结论的序号填在横线上).
15.如图,在平行四边形ABCD中,按以下步骤作图:①以点A为圆心,任意长为半径作弧,分别交AB、AD于点M、N;②分别以点M、N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线AP,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD的周长为 .
16.(2024广安中考)如图,在 ABCD中,AB=4,AD=5,∠ABC=30°,点M为直线BC上一动点,则MA+MD的最小值为 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(7分)(2024泸州中考)如图,在 ABCD中,E、F是对角线BD上的点,且DE=BF.
求证:∠1=∠2.
18.(7分)如图,在 ABCD中,E是BC边上一点,连结AE、AC、ED,AE=AB.
求证:AC=DE.
19.(8分)如图,在4×4的方格子中,△ABC的三个顶点都在格点上.
(1)在图1中画出线段CD,使CD⊥CB,其中点D是格点.
(2)在图2中画出平行四边形ABEC,其中点E是格点.
图1 图2
20.(8分)如图,在四边形ABCD中,AD∥BC,点E为CD边上的中点,连结AE并延长,与BC的延长线交于点F,连结AC、DF.求证:四边形ACFD是平行四边形.
21.(8分)如图,点E、F分别在 ABCD的边BA、DC的延长线上,连结EF,交对角线BD于点O,已知OE=OF,连结DE、BF.试猜想线段BE与DF的数量关系,并加以证明.
22.(8分)如图,在等腰三角形ABC中,∠ACB=90°,AC=BC=10,将△ABC绕点B沿顺时针方向旋转90°得到△A1BC1.
(1)线段A1C1的长度是 ,∠CBA1的度数是 .
(2)连结CC1,求证:四边形CBA1C1是平行四边形.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,在 ABCD中,在BC上取一点E,使得DE=AD,在DE上取一点F,使得∠AFE=∠ADC.
求证:(1)∠AFD=∠C.
(2)DF=EC.
24.(10分)(2024浙江中考)尺规作图问题:
如图1,点E是 ABCD边AD上一点(不包含A、D),连结CE.用尺规作AF∥CE,F是边BC上一点.
小明:如图2.以C为圆心,AE长为半径作弧,交BC于点F,连结AF,则AF∥CE.
小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连结AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦……我明白了!
(1)证明:AF∥CE.
(2)指出小丽作法中存在的问题.
25.(10分)如图,在四边形ABCD中,AD∥BC,延长BC到点E,使CE=BC,连结AE交CD于点F,点F是CD的中点.
求证:(1)△ADF≌△ECF.
(2)四边形ABCD是平行四边形.
26.(10分)如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
(1)线段BE与线段CD的数量关系: .
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0°<α<360°).
①(1)中的结论是否成立 若成立,请利用图2证明;若不成立,请说明理由.
②当AC=ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形 若存在,请直接写出角α的度数;若不存在,请说明理由.
27.(12分)如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧点P从点A出发沿射线AD以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连结 PE,设点P的运动时间为t s.
(1)若PE⊥BC,求BQ的长.
(2)请问是否存在t的值,使以A、B、E、P为顶点的四边形为平行四边形 若存在,求出t的值,若不存在,请说明理由.
【详解答案】
1.D 解析:由题意可知OA=OC,∠AOD=∠COB,OD=OB,
∴△AOD≌△COB.故选D.
2.B
3.B 解析:平行四边形的对角线各自的一半与已知边组成三角形,利用三角形的三边关系可以得出结论.故选B.
4.D 解析:∵四边形ABCD是平行四边形,∠B=100°,∴∠D=∠B=100°,∵AB∥CD,∴∠DEA=∠EAB,∵AE平分∠DAB,∴∠DAE=∠EAB,∴∠DAE=∠DEA,
∴∠DEA=(180°-∠D)=40°,故选D.
5.C 解析:∵四边形ABCD是平行四边形,∴OA=OC,即AC=2OA,∵AC=2AB,∴AB=OA,∴∠ABO=∠AOB=(180°-∠BAO)=43°,∴∠AOD=∠ABO+∠BAO=43°+94°=137°.故选C.
6.D 解析:以①④作为条件,能够判定四边形ABCD是平行四边形.理由:∵AB∥CD,∴∠OAB=∠OCD.在△AOB和△COD中,∠OAB=∠OCD, AO=CO,∠AOB=∠COD,∴△AOB≌△COD(A.S.A.),∴OB=OD,∴四边形ABCD是平行四边形.故选D.
7.C 解析:在 ABCD中,AB=8,
∴CD=AB=8,AB∥CD.
∵AE=3,∴BE=AB-AE=5.
∵CF∥DE,∴四边形DEFC是平行四边形.
∴CD=EF=8.∴BF=EF-BE=8-5=3.故选C.
8.C 解析:由折叠的性质可知,∠GEF=∠DEF=60°.∵AD∥BC,∴∠GFE=∠DEF=60°.∴△GEF是等边三角形.又∵EF=6,∴△GEF的周长为18.故选C.
9.A 解析:方案甲中,连结AC,如图所示:
∵四边形ABCD是平行四边形,点O为BD的中点,
∴OB=OD,OA=OC,
∵BN=NO,OM=MD,
∴NO=OM,
∴四边形ANCM为平行四边形,方案甲正确;
方案乙中,∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABN=∠CDM,
∵AN⊥BD,CM⊥BD,
∴∠ANB=∠CMD=90°,
∴AN∥CM,在△ABN和△CDM中,
∴△ABN≌△CDM.∴AN=CM,
又∵AN∥CM,
∴四边形ANCM为平行四边形,方案乙正确;
方案丙中,∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,AB=CD,AB∥CD,
∴∠ABN=∠CDM,
∵AN平分∠BAD,CM平分∠BCD,
∴∠BAN=∠DCM,
在△ABN和△CDM中,
∴△ABN≌△CDM(A.S.A.),
∴AN=CM,∠ANB=∠CMD,
∴∠ANM=∠CMN,∴AN∥CM,
∴四边形ANCM为平行四边形,方案丙正确.故选A.
10.C 解析:∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,∠A=∠C,故①③正确;
∴S△ABD=S△CDB=S ABCD,∠ODE=∠OBF,
∵点O是BD的中点,∴OD=OB,
又∵∠DOE=∠BOF,∴△ODE≌△OBF(A.S.A.),
∴S△ODE=S△OBF,EO=FO≠ED,故②不正确;
∵S△ABD=S△CDB,S△ODE=S△OBF,
∴S△ABD-S△ODE=S△CDB-S△OBF,
即S四边形ABOE=S四边形CDOF,故④正确.
综上所述,正确结论的个数为3,
故选C.
11.∠B=∠D(答案不唯一)
12.10 解析:∵平行四边形的周长为32 cm,∴邻边和为16 cm.又∵相邻两边之比为3∶5,则这个平行四边形较长的边长为10 cm.
13.130 解析:如图,在 ABCD中,∠A+∠C=100°,∠A=∠C,AB∥CD,∴∠A=∠C=50°,∠C+∠B=180°,∴∠B=180°-∠C=130°.
14.①② 解析:首先由折叠知MN=DN,∠AND=∠ANM,再由平行四边形的性质知∠AND=∠NAM,所以∠NAM=∠ANM,因此AM=MN,所以结论②是正确的.又因为∠DAN=∠MAN,所以∠DAN=∠ANM,所以AD∥MN,因为AD∥BC,所以MN∥BC,所以结论①是正确的.
15.15 解析:由题意可知,AQ是∠BAD的平分线,∴∠DAQ=∠BAQ.∵四边形ABCD是平行四边形,∴AB∥CD.∴∠DQA=∠BAQ.∴∠DQA=∠DAQ.∴DQ=DA=BC=3.∵DQ=2QC,∴QC=1.5,∴CD=3+1.5=4.5.∴平行四边形ABCD的周长为2(BC+CD)=2×(3+4.5)=2×7.5=15.
16. 解析:如图,作点A关于直线BC的对称点A',连结A'D交BC于点M',则AH=A'H,AH⊥BC,AM'=A'M',
∴当M,M'重合时,MA+MD最小,最小值为A'D,
∵AB=4,∠ABC=30°,
∴A'B=4,∠A'BC=30°,
∴∠ABA'=60°,△ABA'是等边三角形,
∴AA'=AB=4,∵AA'⊥BC,BC∥AD,∴AA'⊥AD,
∵AD=5,
∴A'D==.
17.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADE=∠CBF.
在△ADE和△CBF中,
∴△ADE≌△CBF(S.A.S.),
∴∠1=∠2.
18.证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠DAE=∠AEB.
∵AB=AE,∴∠AEB=∠B.
∴∠B=∠DAE.
在△ABC和△EAD中,
∴△ABC≌△EAD(S.A.S.).
∴AC=DE.
19.解:(1)如图1,线段CD就是所求作的图形.
图1
(2)如图2,平行四边形ABEC就是所求作的图形.
图2
20.证明:∵AD∥BC,
∴∠ADE=∠FCE.
∵E为CD的中点,∴CE=DE,
在△ADE和△FCE中,
∠ADE=∠FCE, DE=CE,
∠AED=∠FEC,
∴△ADE≌△FCE(A.S.A.),
∴AE=FE,
∵DE=CE,
∴四边形ACFD是平行四边形.
21.解:BE=DF.
证明如下:
在 ABCD中,BE∥ FD,则
∠EBO=∠FDO.
在△BOE与△DOF 中,
∴△BOE≌△DOF(A.A.S.),
∴BE=DF.
22.解:(1)10 135°
(2)证明:∵∠A1C1B=∠C1BC=90°,∴A1C1∥BC.
又∵A1C1=AC=BC,
∴四边形CBA1C1是平行四边形.
23.证明:(1)四边形ABCD是平行四边形,∴AD∥BC,
∴∠C+∠ADC=180°.
∵∠AFD+∠AFE=180°,
∠AFE=∠ADC,
∴∠AFD=∠C.
(2)∵AD∥BC,∴∠ADF=∠DEC.
在△AFD和△DCE中,
∵∠ADF=∠DEC,∠AFD=∠C,AD=DE,
∴△AFD≌△DCE(A.A.S.),
∴DF=EC.
24.解:(1)证明:根据小明的作法知,CF=AE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵CF=AE,
∴四边形AFCE是平行四边形,
∴AF∥CE.
(2)以A为圆心,EC为半径画弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.
故小丽的作法有问题.
25.证明:(1)∵AD∥BC,
∴∠DAF=∠E.
∵点F是CD的中点,∴DF=CF.
在△ADF与△ECF中,
∴△ADF≌△ECF(A.A.S.).
(2)∵△ADF≌△ECF,∴AD=EC.
∵CE=BC,∴AD=BC.
∵AD∥BC,∴四边形ABCD是平行四边形.
26.解:(1)BE=CD
(2)①成立.
证明:∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD.
由旋转得∠BAE=∠CAD,
∴△BAE≌△CAD(S.A.S.).∴BE=CD.
②存在,角α的度数是45°或225°或315°.
27.解:(1)过点A作AM⊥BC于点M,设PE交AC于点N.如图所示,
∵∠BAC=90°,∠B=45°,
∴AB=AC,
∵AM⊥BC,
∴BM=CM,∠BAM=∠CAM=45°=∠B=∠C,
∴AM=BM=CM=BC=5,
∵AD∥BC,∴∠PAN=∠C=45°,
∵PE⊥BC,
∴PE=AM=5,PE⊥AD,
∴△APN和△CEN是等腰直角三角形,
∴PN=AP=t,CE=NE=5-t,
∵CE=CQ-QE=2t-2,
∴5-t=2t-2,解得t=,
∴BQ=BC-CQ=10-2×=.
(2)存在.
若以A、B、E、P为顶点的四边形为平行四边形,
则AP=BE,
∴t=10-2t+2 或t=2t-2-10,
解得t=4或12,
∴存在t的值,使以A、B、E、P为顶点的四边形为平行四边形,此时t=4或12.
