第19章 矩形、菱形与正方形 评估测试卷(含答案)2024-2025学年数学华东师大版八年级下册
文档属性
| 名称 | 第19章 矩形、菱形与正方形 评估测试卷(含答案)2024-2025学年数学华东师大版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 306.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 14:03:22 | ||
图片预览




文档简介
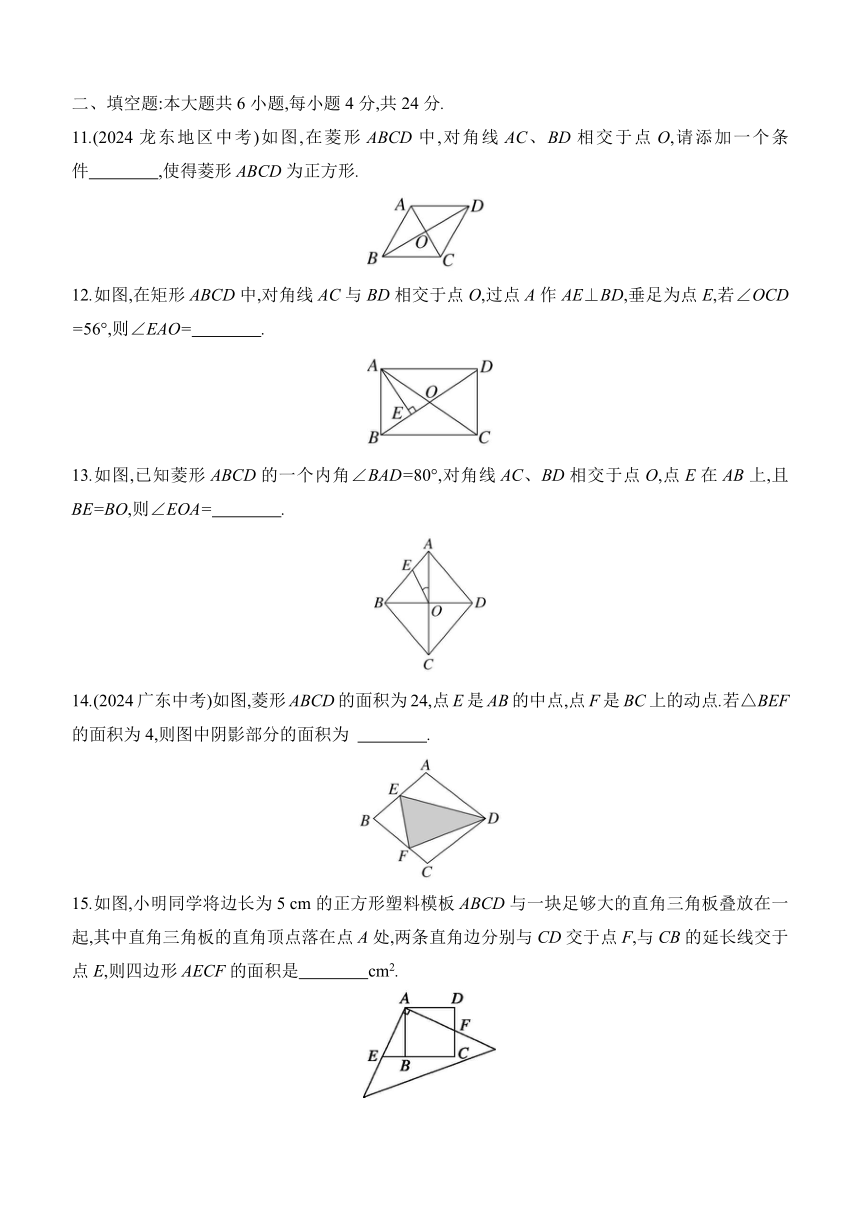
第19章 矩形、菱形与正方形评估测试卷
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.下列判断错误的是 ( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线互相垂直且平分的四边形是正方形
2.如图,矩形ABCD的对角线 AC与BD相交于点O,∠AOD=120°,OC=1,则BC= ( )
A. B.2 C. D.3
3. ABCD中,添加一个条件就成为矩形,则添加的条件是 ( )
A.AB=CD B.∠B+∠D=180°
C.AC=AD D.对角线互相垂直
4.如图,小明用四根长度相同的木条制作能够活动的菱形学具,他先把活动学具做成图1所示的菱形,并测得∠B=60°,对角线AC=1 cm,接着把活动学具做成图2所示的正方形,则图2中对角线AC的长为 ( )
A. cm B.2 cm C.3 cm D.4 cm
5.如图,矩形ABCD的长AD=15 cm,宽AB=10 cm,∠ABC的平分线分AD边为AE、ED两部分,则AE、ED的长分别为 ( )
A.10 cm和5 cm B.11 cm和4 cm
C.9 cm和6 cm D.8 cm和7 cm
6.(2024辽宁中考)如图,在矩形ABCD中,点E在AD上,当△EBC是等边三角形时,∠AEB为 ( )
A.30° B.45° C.60° D.120°
7.如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=60°,则∠2的度数为 ( )
A.30° B.45° C.60° D.75°
8.如图,在菱形ABCD中,点M、N分别在AB、CD上,且AM=CN,MN与AC交于点O,连结BO.若∠DAC=28°,则∠OBC的度数为 ( )
A.28° B.52° C.62° D.72°
9.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F、G,则EF+EG= ( )
A.5 B.6 C. D.8
10.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF,其中正确的有 ( )
A.①②③ B.②③④ C.①③④ D.①②④
二、填空题:本大题共6小题,每小题4分,共24分.
11.(2024龙东地区中考)如图,在菱形ABCD中,对角线AC、BD相交于点O,请添加一个条件 ,使得菱形ABCD为正方形.
12.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠OCD =56°,则∠EAO= .
13.如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上,且BE=BO,则∠EOA= .
14.(2024广东中考)如图,菱形ABCD的面积为24,点E是AB的中点,点F是BC上的动点.若△BEF的面积为4,则图中阴影部分的面积为 .
15.如图,小明同学将边长为5 cm的正方形塑料模板ABCD与一块足够大的直角三角板叠放在一起,其中直角三角板的直角顶点落在点A处,两条直角边分别与CD交于点F,与CB的延长线交于点E,则四边形AECF的面积是 cm2.
16.如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠MCE=15°,过点D作DF⊥CM,垂足为点F,若DF=5,则对角线BD的长为 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(7分)(2024陕西中考)如图,四边形ABCD是矩形,点E和点F在边BC上,且BE=CF.
求证:AF=DE.
18.(7分)如图,矩形ABCD的对角线AC与BD相交于点O,CD∥OE,直线CE是线段OD的垂直平分线,CE分别交OD、AD于点F、G,连结DE.判断四边形OCDE的形状,并说明理由.
19.(8分)按如图所示的方法分别以AB和AC为边作正方形ABDE和正方形AGFC,连结CE、BG.
求证:△ACE≌△AGB.
20.(8分)如图,直线l1∥l2,直线l3分别交直线l1、l2于点A、B.结合图中的作图痕迹,判断四边形ABCD的形状,并说明理由.
21.(8分)如图,已知点A、D、C、B在同一条直线上,且AD=BC,AE=BF,CE=DF.
(1)求证:AE∥BF.
(2)若DF=FC时,求证:四边形DECF是菱形.
22.(8分)如图, ABCD的对角线AC、BD相交于点O.E、F是AC上的两点,并且AE=CF,连结 DE、BF.
(1)求证:△DOE≌△BOF.
(2)若 BD=EF,连结BE、DF,判断四边形EBFD的形状,并说明理由.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.
(1)求证:∠ADB=∠CDB.
(2)若∠ADC=90°,求证:四边形MPND是正方形.
24.(10分)(2024兰州中考)如图,在△ABC中,AB=AC,D是BC的中点,CE∥AD,AE⊥AD,EF⊥AC.
(1)求证:四边形ADCE是矩形.
(2)若BC=4,CE=3,求EF的长.
25.(10分)如图1,在正方形ABCD中,点E、F分别是边AD、DC上的点,且AF⊥BE.
(1)求证:AF=BE.
(2)如图2,在正方形ABCD中,点M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ,判断MP与NQ是否相等 并说明理由.
26.(10分)【猜想结论】
如图1,在△ABC中,点D、E分别是边AB、AC的中点,可以根据度量或目测猜想结论:DE∥BC,且DE=BC.
【验证结论】
如图2,在△ABC中,点D、E分别是边AB、AC 的中点,延长DE至F,使得EF=DE,连结FC.求证:DE∥BC,DE=BC.
【应用结论】
如图3,在四边形 ABCD中,点E、F、G、H分别为边AB、BC、CD、DA 的中点,顺次连结四边形ABCD各边中点得到的新四边形EFGH称为四边形ABCD的中点四边形,应用上述验证结论,求解下列问题:
(1)证明:四边形EFGH是平行四边形.
(2)当AC、BD满足 时,四边形EFGH是矩形.
(3)当AC、BD满足 时,四边形EFGH是正方形.
27.(12分)数学活动课上,老师让同学们以“在矩形纸片上折出60°的角”为主题开展数学活动,经过讨论,第一小组同学的操作步骤如下:
第一步:如图,将矩形纸片ABCD对折,使得AD与BC重合,得到折痕MN,把纸片展平;
第二步:再一次沿过点B的直线折叠纸片,使得点A与MN上的E点重合,折痕与AD交于点F.再把纸片展平.
(1)请用无刻度直尺和圆规在图中作出点E(保留作图痕迹,不写作法).
(2)求证:∠ABE=60°.
(3)若 EN=DF,判断△BCF的形状,并说明理由.
【详解答案】
1.D 2.C 3.B
4.A 解析:如图1,连结AC,
图1 图2
∵四边形ABCD是菱形,∴AB=BC.
∵∠B=60°,∴△ABC是等边三角形.
∴AC=AB=1 cm.
如图2,
∵四边形ABCD是正方形,
∴AB=BC=1 cm,∠B=90°.
∴AC==(cm).故选A.
5.A 解析:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=15 cm.
∴∠AEB=∠EBC.
∵BE平分∠ABC,
∴∠ABE=∠EBC=45°.
∴∠AEB=∠ABE.∴AB=AE=10 cm.
∴DE=AD-AE=5 cm.故选A.
6.C 解析:∵△EBC是等边三角形,∴∠CBE=60°,∵四边形ABCD是矩形,∴AD∥BC,∴∠AEB=∠CBE=60°.故选C.
7.C 解析:过点D作DE∥a,如图.∵四边形ABCD是矩形,∴∠BAD=∠ADC=90°.∴∠3=90°-∠1=90°-60°=30°.∵a∥b,∴DE∥a∥b.∴∠4=∠3=30°,∠2=∠5.∴∠2=∠5=90°-∠4=90°-30°=60°.故选C.
8.C 解析:在菱形ABCD中,AB∥CD,∴∠BAC=∠DCA=∠DAC=28°.又∵AM=CN,∠AOM=∠CON,∴△AMO≌△CNO(A.A.S.).∴AO=CO.∴O是菱形ABCD对角线的交点.∴∠BCO=∠DCA=28°,∠BOC=90°.∴∠OBC=90°-∠BCO=62°.故选C.
9.C 解析:如图,连结OE,
∵四边形ABCD是矩形,∴∠ABC=90°.BC=AD=12,AO=CO=BO=DO.∵AB=5,BC=12,∴AC==13.∴OB=OC=.∴S△BOC=S△BOE+S△COE=OB·EG+OC·EF=S△ABC=××5×12=15.∴×EG+×EF=×(EG+EF)=15.∴EG+EF=.故选C.
10.D 解析:∵四边形ABCD是正方形,
∴∠BAF=∠D=90°,
AB=AD=CD,
∵CE=DF,∴AD-DF=CD-CE,即AF=DE,
在△ABF 和△DAE中,
∴△ABF≌△DAE(S.A.S.),
∴AE=BF,∠ABF=∠DAE,故①正确;
∵∠DAE+∠BAO=90°,
∴∠ABF+∠BAO=90°,
∴∠AOB=180°-(∠ABF+∠BAO)=180°-90°=90°,
∴AE⊥BF,故②正确;
假设AO=OE,如图,连结BE,
∵AE⊥BF,∴AB=BE,
∵在Rt△BCE 中,BE>BC,
∴AB>BC,这与正方形的边AB=BC相矛盾,
假设不成立,AO≠OE,故③错误;
∵△ABF≌△DAE,
∴S△ABF=SDAE,
∴S△ABF-S△AOF=S△DAE-S△AOF,
∴S△AOB=S四边形DEOF,故④正确.
综上所述,正确的有①②④.故选D.
11.AC=BD(答案不唯一) 解析:添加AC=BD,
∵四边形ABCD是菱形,AC=BD,
∴菱形ABCD为正方形.(答案不唯一)
12.22° 13.25°
14.10 解析:如图,连结BD,∵E是AB的中点,∴S△AED=S△ABD=S菱形ABCD=6,
连结EC,同理可得S△BEC=S△AED=6,
∵S△BEF=4,∴S△BEF=S△BEC,
∴FC=BC,
∴S△DFC=S△BCD=S菱形ABCD=4,
∴S阴影=S菱形ABCD-S△AED-S△BEF-S△DFC=24-6-4-4=10.
15.25 解析:∵四边形ABCD是正方形,
∴∠BAD=∠ABC=∠D=90°,AB=AD.
∴∠DAF+∠BAF=90°.
∵∠EAF=90°,
∴∠EAB+∠BAF=90°.
∴∠EAB=∠DAF.
在△EAB和△FAD中,
∴△EAB≌△FAD(A.S.A.).
∴S△EAB=S△FAD.
∵S四边形AECF=S四边形ABCF+S△ABE,
∴S四边形AECF=S四边形ABCF+S△ADF=S正方形ABCD=52=25(cm2).
16.10 解析:如图,连结AC交BD于点H,由菱形的性质得∠DHC=90°,∠DCE=70°.又∵∠MCE=15°,
∴∠DCF=55°.∵DF⊥CM,∴∠CDF=35°.
又∵四边形ABCD是菱形,
∴DB平分∠ADC.
∴∠HDC=35°.
在△CDH和△CDF中,
∴△CDH≌△CDF(A.A.S.).
∴DH=DF=5.∴BD=10.
17.证明:∵四边形ABCD为矩形,
∴AB=CD,∠B=∠C=90°,
∵BE=CF,
∴BE+EF=CF+EF.
即BF=CE,
在△ABF和△DCE中,
∴△ABF≌△DCE(S.A.S.),
∴AF=DE.
18.解:四边形OCDE是菱形.
理由如下:
∵矩形ABCD的对角线AC与BD相交于点O,
∴OC=OD=AC=BD.
∵直线CE是线段OD的垂直平分线,
∴CO=CD,EO=ED.
∴CO=CD=OD,即△COD是等边三角形.
∴∠ODC=∠DCO=∠DOC=60°.
∠OCF=∠DCF=∠OCD=30°.
∵CD∥OE,EO=ED,
∴∠EOD=∠EDO=∠CDO=60°.
∴△EOD是等边三角形.
∴CO=CD=EO=ED.
∴四边形OCDE是菱形.
19.证明:∵四边形ABDE和四边形AGFC均为正方形,
∴AE=AB,AC=AG,
∠EAB=∠CAG=90°.
∴∠EAC+∠CAB=∠CAB+∠BAG.
∴∠EAC=∠BAG.
在△ACE和△AGB中,
∴△ACE≌△AGB(S.A.S.).
20.解:四边形 ABCD是菱形.
理由如下:
根据作图过程可知,AB=CB,∠ABD=∠CBD,
∵l1∥l2,∴∠ADB=∠CBD,
∴∠ABD=∠ADB,∴AB=AD,
∴AD=BC,∴四边形ABCD是平行四边形,
∵AB=CB,∴四边形ABCD是菱形.
21.证明:(1)∵AD=BC,
∴AD+DC=BC+DC,即AC=BD.
在△AEC和△BFD中,
∴△AEC≌△BFD(S.S.S.).
∴∠A=∠B.∴AE∥BF.
(2)证法一:在△ADE和△BCF中,
∴△ADE≌△BCF(S.A.S.).
∴DE=CF.又EC=DF,
∴四边形DECF是平行四边形.
∵DF=FC,
∴ DECF是菱形.
证法二:∵△AEC≌△BFD,
∴∠ECA=∠FDB.∴EC∥DF.
又EC=DF,
∴四边形DECF是平行四边形.
∵DF=FC,
∴ DECF是菱形.
22.解:(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.
∵AE=CF,∴OE=OF.
∵在△DOE和△BOF中,
∴△DOE≌△BOF(S.A.S.).
(2)四边形EBFD是矩形.
理由如下:∵OD=OB,OE=OF,
∴四边形EBFD是平行四边形.
∵BD=EF,
∴四边形 EBFD是矩形.
23.证明:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD.
在△ABD和△CBD中,
△ABD≌△CBD(S.A.S.),
∴∠ADB=∠CDB.
(2)∵PM⊥AD,PN⊥CD,
∠PMD=∠PND=90°,
∵∠ADC=90°,∴四边形 MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°,∴∠MPD=45°.
∴PM=MD.
∴四边形MPND是正方形.
24.解:(1)证明:∵在△ABC中,AB=AC,D是BC的中点,∴AD⊥BC,
即∠ADC=∠ADB=90°,
∵CE∥AD,∴∠ECD=∠ADB=90°,
∵AE⊥AD,
∴∠EAD=90°,
∴∠ADC=∠ECD=∠EAD=90°,
∴四边形ADCE是矩形.
(2)∵在△ABC中,AB=AC,D是BC的中点,BC=4,
∴BD=CD=BC=2,
由(1)可知:四边形ADCE是矩形,
∵AE=CD=2,∠AEC=90°,
在Rt△AEC中,AE=2,CE=3,
由勾股定理得
AC==,
∵EF⊥AC,
由三角形的面积公式得
S△AEC=AC·EF=AE·CE,
∴EF===.
25.解:(1)证明:在正方形ABCD中,
AB=AD,∠BAE=∠D=90°,
∴∠DAF+∠BAF=90°.
∵AF⊥BE,∴∠ABE+∠BAF=90°.
∴∠ABE=∠DAF.
在△ABE和△DAF中,
∵∠ABE=∠DAF,AB=DA,∠BAE=∠D,
∴△ABE≌△DAF(A.S.A.).
∴AF=BE.
(2)MP与NQ相等.
理由:如图,过点A作AG∥MP交CD于点G,过点B作BH∥NQ交AD于点H,得到 BNQH和 AMPG,∴AG=MP, BH=NQ.∵MP⊥NQ,∴AG⊥BH.由(1)知AG=BH,∴MP=NQ.
26.解:【验证结论】证明:∵E是AC的中点,
∴AE=CE,
∵∠AED=∠CEF,DE=EF,
∴△AED≌△CEF(S.A.S.).
∴∠A=∠ECF,AD=CF,
∴AB∥CF,
∵D是AB的中点,
∴AD=BD,∴BD=CF,
∴四边形BDFC是平行四边形,
∴DE∥BC,DF=BC,∴DE=BC.
【应用结论】(1)证明:如图,连结BD,
由结论知,EH∥BD,EH=BD,FG∥BD,FG=BD,
∴EH∥FG,EH=FG,∴四边形EFGH是平行四边形.
(2)AC⊥BD
解析:如图,连结BD、AC,BD与AC交于O,BD与HG交于M,
由(1)知,四边形EFGH是平行四边形,
∵AC⊥BD,
∴∠AOD=90°,
由结论知,HG∥AC,
∴∠HMD=∠AOD=90°,
∵EH∥BD,
∴∠EHG=∠HMD=90°,
∴四边形 EFGH是矩形.
(3)AC⊥BD,AC=BD
解析:由结论知,EH=BD,HG=AC,
∵BD=AC,∴EH=HG,
由(2)知,四边形EFGH是矩形,
∴四边形EFGH是正方形.
27.解:(1)如图,点E即为所求.
(2)证明:如图,连结AE、BE,
∵将矩形纸片ABCD对折,使得AD与BC重合,得到折痕MN,
∴MN垂直平分AB,∴AE=BE,
由折叠知,BE=AB,∴BE=AB=AE,
∴△ABE是等边三角形,
∴∠ABE=60°.
(3)△BCF是等边三角形.
理由如下:
如图,过点E作GH⊥AD,交AD于G,交BC于H,连结FE、EC,
∵AD∥BC,∴GH⊥BC,
∴∠GHC=90°,
∵∠EHC=∠HCN=∠CNE=∠END=∠D=∠DGE=90°,
∴四边形GHCD、四边形EHCN、四边形NDGE都是矩形,
∴GE=DN,EH=NC,GD=EN=HC,
∵DN=CN,∴GE=HE,
∵∠EGF=∠EHC,EN=DF,
∴EN=GD=GF=HC,
∴△EGF≌△EHC,
∴EF=EC,
∵∠FEG+∠FEH=180°,
∴∠CEH+∠FEH=180°,
∵F、E、C 三点共线,
∵∠BEF=∠BAF=90°,
即BE⊥FC,
∴BF=BC,
∵∠ABE=60°,
∴∠ABF=∠ABE=30°,
∴∠FBC=90°-∠ABF=60°,
∴△BCF是等边三角形.
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.下列判断错误的是 ( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线互相垂直且平分的四边形是正方形
2.如图,矩形ABCD的对角线 AC与BD相交于点O,∠AOD=120°,OC=1,则BC= ( )
A. B.2 C. D.3
3. ABCD中,添加一个条件就成为矩形,则添加的条件是 ( )
A.AB=CD B.∠B+∠D=180°
C.AC=AD D.对角线互相垂直
4.如图,小明用四根长度相同的木条制作能够活动的菱形学具,他先把活动学具做成图1所示的菱形,并测得∠B=60°,对角线AC=1 cm,接着把活动学具做成图2所示的正方形,则图2中对角线AC的长为 ( )
A. cm B.2 cm C.3 cm D.4 cm
5.如图,矩形ABCD的长AD=15 cm,宽AB=10 cm,∠ABC的平分线分AD边为AE、ED两部分,则AE、ED的长分别为 ( )
A.10 cm和5 cm B.11 cm和4 cm
C.9 cm和6 cm D.8 cm和7 cm
6.(2024辽宁中考)如图,在矩形ABCD中,点E在AD上,当△EBC是等边三角形时,∠AEB为 ( )
A.30° B.45° C.60° D.120°
7.如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=60°,则∠2的度数为 ( )
A.30° B.45° C.60° D.75°
8.如图,在菱形ABCD中,点M、N分别在AB、CD上,且AM=CN,MN与AC交于点O,连结BO.若∠DAC=28°,则∠OBC的度数为 ( )
A.28° B.52° C.62° D.72°
9.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F、G,则EF+EG= ( )
A.5 B.6 C. D.8
10.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF,其中正确的有 ( )
A.①②③ B.②③④ C.①③④ D.①②④
二、填空题:本大题共6小题,每小题4分,共24分.
11.(2024龙东地区中考)如图,在菱形ABCD中,对角线AC、BD相交于点O,请添加一个条件 ,使得菱形ABCD为正方形.
12.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠OCD =56°,则∠EAO= .
13.如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上,且BE=BO,则∠EOA= .
14.(2024广东中考)如图,菱形ABCD的面积为24,点E是AB的中点,点F是BC上的动点.若△BEF的面积为4,则图中阴影部分的面积为 .
15.如图,小明同学将边长为5 cm的正方形塑料模板ABCD与一块足够大的直角三角板叠放在一起,其中直角三角板的直角顶点落在点A处,两条直角边分别与CD交于点F,与CB的延长线交于点E,则四边形AECF的面积是 cm2.
16.如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠MCE=15°,过点D作DF⊥CM,垂足为点F,若DF=5,则对角线BD的长为 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(7分)(2024陕西中考)如图,四边形ABCD是矩形,点E和点F在边BC上,且BE=CF.
求证:AF=DE.
18.(7分)如图,矩形ABCD的对角线AC与BD相交于点O,CD∥OE,直线CE是线段OD的垂直平分线,CE分别交OD、AD于点F、G,连结DE.判断四边形OCDE的形状,并说明理由.
19.(8分)按如图所示的方法分别以AB和AC为边作正方形ABDE和正方形AGFC,连结CE、BG.
求证:△ACE≌△AGB.
20.(8分)如图,直线l1∥l2,直线l3分别交直线l1、l2于点A、B.结合图中的作图痕迹,判断四边形ABCD的形状,并说明理由.
21.(8分)如图,已知点A、D、C、B在同一条直线上,且AD=BC,AE=BF,CE=DF.
(1)求证:AE∥BF.
(2)若DF=FC时,求证:四边形DECF是菱形.
22.(8分)如图, ABCD的对角线AC、BD相交于点O.E、F是AC上的两点,并且AE=CF,连结 DE、BF.
(1)求证:△DOE≌△BOF.
(2)若 BD=EF,连结BE、DF,判断四边形EBFD的形状,并说明理由.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.
(1)求证:∠ADB=∠CDB.
(2)若∠ADC=90°,求证:四边形MPND是正方形.
24.(10分)(2024兰州中考)如图,在△ABC中,AB=AC,D是BC的中点,CE∥AD,AE⊥AD,EF⊥AC.
(1)求证:四边形ADCE是矩形.
(2)若BC=4,CE=3,求EF的长.
25.(10分)如图1,在正方形ABCD中,点E、F分别是边AD、DC上的点,且AF⊥BE.
(1)求证:AF=BE.
(2)如图2,在正方形ABCD中,点M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ,判断MP与NQ是否相等 并说明理由.
26.(10分)【猜想结论】
如图1,在△ABC中,点D、E分别是边AB、AC的中点,可以根据度量或目测猜想结论:DE∥BC,且DE=BC.
【验证结论】
如图2,在△ABC中,点D、E分别是边AB、AC 的中点,延长DE至F,使得EF=DE,连结FC.求证:DE∥BC,DE=BC.
【应用结论】
如图3,在四边形 ABCD中,点E、F、G、H分别为边AB、BC、CD、DA 的中点,顺次连结四边形ABCD各边中点得到的新四边形EFGH称为四边形ABCD的中点四边形,应用上述验证结论,求解下列问题:
(1)证明:四边形EFGH是平行四边形.
(2)当AC、BD满足 时,四边形EFGH是矩形.
(3)当AC、BD满足 时,四边形EFGH是正方形.
27.(12分)数学活动课上,老师让同学们以“在矩形纸片上折出60°的角”为主题开展数学活动,经过讨论,第一小组同学的操作步骤如下:
第一步:如图,将矩形纸片ABCD对折,使得AD与BC重合,得到折痕MN,把纸片展平;
第二步:再一次沿过点B的直线折叠纸片,使得点A与MN上的E点重合,折痕与AD交于点F.再把纸片展平.
(1)请用无刻度直尺和圆规在图中作出点E(保留作图痕迹,不写作法).
(2)求证:∠ABE=60°.
(3)若 EN=DF,判断△BCF的形状,并说明理由.
【详解答案】
1.D 2.C 3.B
4.A 解析:如图1,连结AC,
图1 图2
∵四边形ABCD是菱形,∴AB=BC.
∵∠B=60°,∴△ABC是等边三角形.
∴AC=AB=1 cm.
如图2,
∵四边形ABCD是正方形,
∴AB=BC=1 cm,∠B=90°.
∴AC==(cm).故选A.
5.A 解析:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=15 cm.
∴∠AEB=∠EBC.
∵BE平分∠ABC,
∴∠ABE=∠EBC=45°.
∴∠AEB=∠ABE.∴AB=AE=10 cm.
∴DE=AD-AE=5 cm.故选A.
6.C 解析:∵△EBC是等边三角形,∴∠CBE=60°,∵四边形ABCD是矩形,∴AD∥BC,∴∠AEB=∠CBE=60°.故选C.
7.C 解析:过点D作DE∥a,如图.∵四边形ABCD是矩形,∴∠BAD=∠ADC=90°.∴∠3=90°-∠1=90°-60°=30°.∵a∥b,∴DE∥a∥b.∴∠4=∠3=30°,∠2=∠5.∴∠2=∠5=90°-∠4=90°-30°=60°.故选C.
8.C 解析:在菱形ABCD中,AB∥CD,∴∠BAC=∠DCA=∠DAC=28°.又∵AM=CN,∠AOM=∠CON,∴△AMO≌△CNO(A.A.S.).∴AO=CO.∴O是菱形ABCD对角线的交点.∴∠BCO=∠DCA=28°,∠BOC=90°.∴∠OBC=90°-∠BCO=62°.故选C.
9.C 解析:如图,连结OE,
∵四边形ABCD是矩形,∴∠ABC=90°.BC=AD=12,AO=CO=BO=DO.∵AB=5,BC=12,∴AC==13.∴OB=OC=.∴S△BOC=S△BOE+S△COE=OB·EG+OC·EF=S△ABC=××5×12=15.∴×EG+×EF=×(EG+EF)=15.∴EG+EF=.故选C.
10.D 解析:∵四边形ABCD是正方形,
∴∠BAF=∠D=90°,
AB=AD=CD,
∵CE=DF,∴AD-DF=CD-CE,即AF=DE,
在△ABF 和△DAE中,
∴△ABF≌△DAE(S.A.S.),
∴AE=BF,∠ABF=∠DAE,故①正确;
∵∠DAE+∠BAO=90°,
∴∠ABF+∠BAO=90°,
∴∠AOB=180°-(∠ABF+∠BAO)=180°-90°=90°,
∴AE⊥BF,故②正确;
假设AO=OE,如图,连结BE,
∵AE⊥BF,∴AB=BE,
∵在Rt△BCE 中,BE>BC,
∴AB>BC,这与正方形的边AB=BC相矛盾,
假设不成立,AO≠OE,故③错误;
∵△ABF≌△DAE,
∴S△ABF=SDAE,
∴S△ABF-S△AOF=S△DAE-S△AOF,
∴S△AOB=S四边形DEOF,故④正确.
综上所述,正确的有①②④.故选D.
11.AC=BD(答案不唯一) 解析:添加AC=BD,
∵四边形ABCD是菱形,AC=BD,
∴菱形ABCD为正方形.(答案不唯一)
12.22° 13.25°
14.10 解析:如图,连结BD,∵E是AB的中点,∴S△AED=S△ABD=S菱形ABCD=6,
连结EC,同理可得S△BEC=S△AED=6,
∵S△BEF=4,∴S△BEF=S△BEC,
∴FC=BC,
∴S△DFC=S△BCD=S菱形ABCD=4,
∴S阴影=S菱形ABCD-S△AED-S△BEF-S△DFC=24-6-4-4=10.
15.25 解析:∵四边形ABCD是正方形,
∴∠BAD=∠ABC=∠D=90°,AB=AD.
∴∠DAF+∠BAF=90°.
∵∠EAF=90°,
∴∠EAB+∠BAF=90°.
∴∠EAB=∠DAF.
在△EAB和△FAD中,
∴△EAB≌△FAD(A.S.A.).
∴S△EAB=S△FAD.
∵S四边形AECF=S四边形ABCF+S△ABE,
∴S四边形AECF=S四边形ABCF+S△ADF=S正方形ABCD=52=25(cm2).
16.10 解析:如图,连结AC交BD于点H,由菱形的性质得∠DHC=90°,∠DCE=70°.又∵∠MCE=15°,
∴∠DCF=55°.∵DF⊥CM,∴∠CDF=35°.
又∵四边形ABCD是菱形,
∴DB平分∠ADC.
∴∠HDC=35°.
在△CDH和△CDF中,
∴△CDH≌△CDF(A.A.S.).
∴DH=DF=5.∴BD=10.
17.证明:∵四边形ABCD为矩形,
∴AB=CD,∠B=∠C=90°,
∵BE=CF,
∴BE+EF=CF+EF.
即BF=CE,
在△ABF和△DCE中,
∴△ABF≌△DCE(S.A.S.),
∴AF=DE.
18.解:四边形OCDE是菱形.
理由如下:
∵矩形ABCD的对角线AC与BD相交于点O,
∴OC=OD=AC=BD.
∵直线CE是线段OD的垂直平分线,
∴CO=CD,EO=ED.
∴CO=CD=OD,即△COD是等边三角形.
∴∠ODC=∠DCO=∠DOC=60°.
∠OCF=∠DCF=∠OCD=30°.
∵CD∥OE,EO=ED,
∴∠EOD=∠EDO=∠CDO=60°.
∴△EOD是等边三角形.
∴CO=CD=EO=ED.
∴四边形OCDE是菱形.
19.证明:∵四边形ABDE和四边形AGFC均为正方形,
∴AE=AB,AC=AG,
∠EAB=∠CAG=90°.
∴∠EAC+∠CAB=∠CAB+∠BAG.
∴∠EAC=∠BAG.
在△ACE和△AGB中,
∴△ACE≌△AGB(S.A.S.).
20.解:四边形 ABCD是菱形.
理由如下:
根据作图过程可知,AB=CB,∠ABD=∠CBD,
∵l1∥l2,∴∠ADB=∠CBD,
∴∠ABD=∠ADB,∴AB=AD,
∴AD=BC,∴四边形ABCD是平行四边形,
∵AB=CB,∴四边形ABCD是菱形.
21.证明:(1)∵AD=BC,
∴AD+DC=BC+DC,即AC=BD.
在△AEC和△BFD中,
∴△AEC≌△BFD(S.S.S.).
∴∠A=∠B.∴AE∥BF.
(2)证法一:在△ADE和△BCF中,
∴△ADE≌△BCF(S.A.S.).
∴DE=CF.又EC=DF,
∴四边形DECF是平行四边形.
∵DF=FC,
∴ DECF是菱形.
证法二:∵△AEC≌△BFD,
∴∠ECA=∠FDB.∴EC∥DF.
又EC=DF,
∴四边形DECF是平行四边形.
∵DF=FC,
∴ DECF是菱形.
22.解:(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.
∵AE=CF,∴OE=OF.
∵在△DOE和△BOF中,
∴△DOE≌△BOF(S.A.S.).
(2)四边形EBFD是矩形.
理由如下:∵OD=OB,OE=OF,
∴四边形EBFD是平行四边形.
∵BD=EF,
∴四边形 EBFD是矩形.
23.证明:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD.
在△ABD和△CBD中,
△ABD≌△CBD(S.A.S.),
∴∠ADB=∠CDB.
(2)∵PM⊥AD,PN⊥CD,
∠PMD=∠PND=90°,
∵∠ADC=90°,∴四边形 MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°,∴∠MPD=45°.
∴PM=MD.
∴四边形MPND是正方形.
24.解:(1)证明:∵在△ABC中,AB=AC,D是BC的中点,∴AD⊥BC,
即∠ADC=∠ADB=90°,
∵CE∥AD,∴∠ECD=∠ADB=90°,
∵AE⊥AD,
∴∠EAD=90°,
∴∠ADC=∠ECD=∠EAD=90°,
∴四边形ADCE是矩形.
(2)∵在△ABC中,AB=AC,D是BC的中点,BC=4,
∴BD=CD=BC=2,
由(1)可知:四边形ADCE是矩形,
∵AE=CD=2,∠AEC=90°,
在Rt△AEC中,AE=2,CE=3,
由勾股定理得
AC==,
∵EF⊥AC,
由三角形的面积公式得
S△AEC=AC·EF=AE·CE,
∴EF===.
25.解:(1)证明:在正方形ABCD中,
AB=AD,∠BAE=∠D=90°,
∴∠DAF+∠BAF=90°.
∵AF⊥BE,∴∠ABE+∠BAF=90°.
∴∠ABE=∠DAF.
在△ABE和△DAF中,
∵∠ABE=∠DAF,AB=DA,∠BAE=∠D,
∴△ABE≌△DAF(A.S.A.).
∴AF=BE.
(2)MP与NQ相等.
理由:如图,过点A作AG∥MP交CD于点G,过点B作BH∥NQ交AD于点H,得到 BNQH和 AMPG,∴AG=MP, BH=NQ.∵MP⊥NQ,∴AG⊥BH.由(1)知AG=BH,∴MP=NQ.
26.解:【验证结论】证明:∵E是AC的中点,
∴AE=CE,
∵∠AED=∠CEF,DE=EF,
∴△AED≌△CEF(S.A.S.).
∴∠A=∠ECF,AD=CF,
∴AB∥CF,
∵D是AB的中点,
∴AD=BD,∴BD=CF,
∴四边形BDFC是平行四边形,
∴DE∥BC,DF=BC,∴DE=BC.
【应用结论】(1)证明:如图,连结BD,
由结论知,EH∥BD,EH=BD,FG∥BD,FG=BD,
∴EH∥FG,EH=FG,∴四边形EFGH是平行四边形.
(2)AC⊥BD
解析:如图,连结BD、AC,BD与AC交于O,BD与HG交于M,
由(1)知,四边形EFGH是平行四边形,
∵AC⊥BD,
∴∠AOD=90°,
由结论知,HG∥AC,
∴∠HMD=∠AOD=90°,
∵EH∥BD,
∴∠EHG=∠HMD=90°,
∴四边形 EFGH是矩形.
(3)AC⊥BD,AC=BD
解析:由结论知,EH=BD,HG=AC,
∵BD=AC,∴EH=HG,
由(2)知,四边形EFGH是矩形,
∴四边形EFGH是正方形.
27.解:(1)如图,点E即为所求.
(2)证明:如图,连结AE、BE,
∵将矩形纸片ABCD对折,使得AD与BC重合,得到折痕MN,
∴MN垂直平分AB,∴AE=BE,
由折叠知,BE=AB,∴BE=AB=AE,
∴△ABE是等边三角形,
∴∠ABE=60°.
(3)△BCF是等边三角形.
理由如下:
如图,过点E作GH⊥AD,交AD于G,交BC于H,连结FE、EC,
∵AD∥BC,∴GH⊥BC,
∴∠GHC=90°,
∵∠EHC=∠HCN=∠CNE=∠END=∠D=∠DGE=90°,
∴四边形GHCD、四边形EHCN、四边形NDGE都是矩形,
∴GE=DN,EH=NC,GD=EN=HC,
∵DN=CN,∴GE=HE,
∵∠EGF=∠EHC,EN=DF,
∴EN=GD=GF=HC,
∴△EGF≌△EHC,
∴EF=EC,
∵∠FEG+∠FEH=180°,
∴∠CEH+∠FEH=180°,
∵F、E、C 三点共线,
∵∠BEF=∠BAF=90°,
即BE⊥FC,
∴BF=BC,
∵∠ABE=60°,
∴∠ABF=∠ABE=30°,
∴∠FBC=90°-∠ABF=60°,
∴△BCF是等边三角形.
