第20章 数据的整理与初步处理 评估测试卷(含答案)2024-2025学年数学华东师大版八年级下册
文档属性
| 名称 | 第20章 数据的整理与初步处理 评估测试卷(含答案)2024-2025学年数学华东师大版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 147.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 00:00:00 | ||
图片预览




文档简介
第20章 数据的整理与初步处理 评估测试卷
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.为增强学生的环保意识,共建绿色文明校园,某学校组织“废纸宝宝旅行记”活动.经统计,七年级5个班级一周回收废纸情况如下表:
班级 一班 二班 三班 四班 五班
废纸重量/kg 4.5 4.4 5.1 3.3 5.7
则每个班级回收废纸的平均重量为 ( )
A.5 kg B.4.8 kg C.4.6 kg D.4.5 kg
2.(2024南充中考)学校举行篮球技能大赛,评委从控球技能和投球技能两方面为选手打分,各项成绩均按百分制计,然后再按控球技能占60%,投球技能占40%计算选手的综合成绩(百分制).选手李林控球技能得90分,投球技能得80分.李林综合成绩为 ( )
A.170分 B.86分 C.85分 D.84分
3.某校运动会前夕,要选60名身高基本相同的女同学组成表演方阵,在这个问题中,最值得关注的是该校所有女生身高的 ( )
A.方差 B.众数 C.平均数 D.中位数
4.小张参加某节目的海选,共有17位选手参加角逐争取8个晋级名额,已知他们的分数互不相同,小张要判断自己是否能够晋级,只需知道这17名选手成绩统计量中的 ( )
A.平均数 B.众数 C.中位数 D.频数
5.小明调查了班级里20位同学本学期购买课外书的花费情况,并将结果绘制成了如图所示的统计图.这20位同学本学期购买课外书的花费的众数和中位数分别是 ( )
A.50元,50元 B.50元,30元 C.80元,50元 D.30元,50元
6.(2024广元中考)在五四文艺晚会节目评选中,某班选送的节目得分如下:91,96,95,92,94,95,95,分析这组数据,下列说法错误的是 ( )
A.中位数是95 B.方差是3
C.众数是95 D.平均数是94
7.某位同学四次射击测试成绩(单位:环)分别为:9,9,x,8,若这组数据的众数与平均数恰好相等,则x的值为 ( )
A.10 B.9 C.8 D.7
8.某校合唱团有30名成员,合唱团成员的年龄分布统计表如下:
年龄/岁 13 14 15 16
频数 5 15 x 10-x
则对于不同的x,下列关于年龄的统计量不会发生改变的是 ( )
A.平均数、中位数 B.平均数、方差
C.众数、中位数 D.众数、方差
9.长时间观看手机、电脑等电子产品对视力影响非常大.6月6日是“全国爱眼日”,为了解学生的视力情况,某学校从甲、乙两个班级各抽取8名学生进行调查,并将统计数据绘制成如图所示的折线统计图,则下列说法正确的是 ( )
A.甲班视力值的平均数大于乙班视力值的平均数
B.甲班视力值的中位数大于乙班视力值的中位数
C.甲班视力值的众数小于乙班视力值的众数
D.甲班视力值的方差小于乙班视力值的方差
10.(2024滨州中考)在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80
人数 2 3 2 3 4 1
某同学分析上表后得出如下结论:
①这些运动员成绩的平均数是1.65 m;
②这些运动员成绩的中位数是1.70 m;
③这些运动员成绩的众数是1.75 m.
上述结论中正确的是 ( )
A.②③ B.①③ C.①② D.①②③
二、填空题:本大题共6小题,每小题4分,共24分.
11.在“献爱心”捐款活动中,某校八年级一班同学人人拿出自己的零花钱,现将同学们的捐款数整理成统计表,则该班同学平均每人捐款 元.
捐款数/元 5 10 20 50
人数/人 4 15 6 5
12.某校开展主题为“我身边的共产党员”的演讲比赛.比赛从演讲内容、演讲技巧、演讲效果三个方面打分,最终得分按4∶3∶3的比例计算.若选手甲在演讲内容、演讲技巧、演讲效果三个方面的得分分别为95分、80分、90分,则选手甲的最终得分为 分.
13.(2024河南中考)2024年3月是第8个全国近视防控宣传教育月,其主题是“有效减少近视发生,共同守护光明未来”.某校组织各班围绕这个主题开展板报宣传活动,并对各班的宣传板报进行评分,得分情况如图,则得分的众数为 分.
14.如果一组数据x1,x2,…,xn的方差是4,那么另一组数据x1+3,x2+3,…,xn+3的方差是 .
15.(2024南充中考)若一组数据6,6,m,7,7,8的众数为7,则这组数据的中位数为 .
16.若四个互不相等的正整数中,最大的数是8,中位数是4,则这四个数的和为 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(7分)某班10名学生在一次数学测验中的成绩以90分为标准,超过的分数记为正数,不足的分数记为负数,如下:-7,-10,+9,+2,-1,+5,-8,+10,+4,+9.求他们的平均成绩.
18.(7分)一组数据从小到大排列为1,2,3,x,4,5,若这组数据的中位数为3,求这组数据的方差.
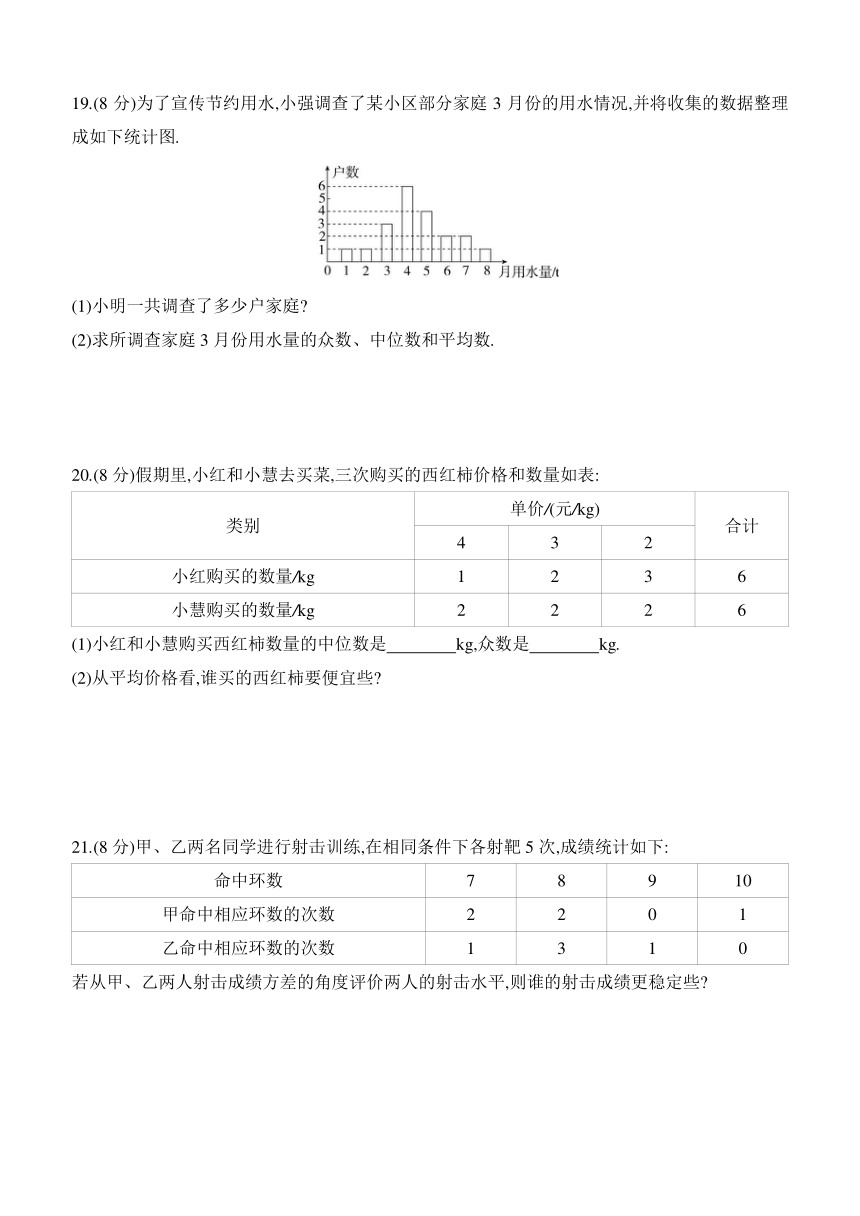
19.(8分)为了宣传节约用水,小强调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
(1)小明一共调查了多少户家庭
(2)求所调查家庭3月份用水量的众数、中位数和平均数.
20.(8分)假期里,小红和小慧去买菜,三次购买的西红柿价格和数量如表:
类别 单价/(元/kg) 合计
4 3 2
小红购买的数量/kg 1 2 3 6
小慧购买的数量/kg 2 2 2 6
(1)小红和小慧购买西红柿数量的中位数是 kg,众数是 kg.
(2)从平均价格看,谁买的西红柿要便宜些
21.(8分)甲、乙两名同学进行射击训练,在相同条件下各射靶5次,成绩统计如下:
命中环数 7 8 9 10
甲命中相应环数的次数 2 2 0 1
乙命中相应环数的次数 1 3 1 0
若从甲、乙两人射击成绩方差的角度评价两人的射击水平,则谁的射击成绩更稳定些
22.(8分)(2024福建中考)已知A、B两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有考生3 000人,数学平均分为90分;乙类学校有考生2 000人,数学平均分为80分.
(1)求A地考生的数学平均分.
(2)若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学平均分一定比A地考生数学平均分高 若能,请给予证明;若不能,请举例说明.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)某机械厂有15名工人,某月这15名工人加工的零件数统计如下:
人数 1 1 2 6 3 2
加工零件数/件 540 450 300 240 210 120
(1)求这15名工人该月加工的零件数的平均数、中位数和众数.
(2)假如部门负责人把每位工人每月加工零件的任务确定为260件,你认为是否合理 为什么 如果不合理,你认为多少较为合适
24.(8分)从某校八年级(1)班和(2)班的一次数学考试成绩中分别抽取10名学生的数学成绩进行分析,成绩(单位:分)如下:
(1)班:50,55,95,80,90,85,100,100,85,60.
(2)班:85,75,70,95,100,90,65,70,80,70.
(1)分别计算这两个班10名学生的平均数学成绩.
(2)分别计算这两个班10名学生数学成绩的方差.
(3)由以上数据,你认为哪一个班实施分层教学、因材施教的效果会更好
25.(10分)某校团委在八、九年级各抽取50名团员开展团知识竞赛活动,为便于统计成绩,制定了取整数的计分方式,满分10分.现将他们的竞赛成绩进行整理、分析,给出了下列图表:
年级 众数/分 中位数/分 方差
八年级 7 8 1.88
九年级 a b 1.56
(1)八年级的平均成绩是8分,九年级的平均成绩是 .
(2)请根据图表中的信息,回答下列问题.
①a= ,b= .
②现要给成绩突出的年级颁奖,你认为应该给哪个年级颁奖
(3)若规定成绩为10分的学生获一等奖,成绩为9分的学生获二等奖,成绩为8分的学生获三等奖,通过计算说明哪个年级的获奖率高.
26.(10分)某校八年级(1)班甲、乙两男生在5次引体向上测试中有效次数如下:甲:8,8,7,8,9;乙:5,9,7,10,9.甲、乙两同学引体向上的平均数、众数、中位数、方差如表:
学生 平均数 众数 中位数 方差
甲 8 b 8 0.4
乙 a 9 c 3.2
根据以上信息,回答下列问题:
(1)表格中a= , b= ,c= .(填数值)
(2)体育老师根据这5次的成绩,决定选择甲同学代表班级参加年级引体向上比赛,选择甲的理由是 .班主任李老师根据去年比赛的成绩(至少9次才能获奖) ,决定选择乙同学代表班级参加年级引体向上比赛,选择乙的理由是 .
(3)如果乙同学再做一次引体向上,有效次数为8,那么乙同学6次引体向上成绩的平均数 ,中位数 ,方差 . (填“变大”“变小”或“不变”)
27.(14分)(2024青海中考)为了解学生物理实验操作情况,抽取小青和小海两名同学的10次实验得分,并对他们的得分情况从以下两方面整理描述如下:
①操作规范性:
②书写准确性:
小青:1 1 2 2 2 3 1 3 2 1
小海:1 2 2 3 3 3 2 1 2 1
操作规范性和书写准确性的得分统计表:
学生 操作规范性 书写准确性
平均数 方差 平均数 中位数
小青 4 1.8 a
小海 4 b 2
根据以上信息,回答下列问题:
(1)表格中的a= ,比较和的大小 .
(2)计算表格中b的值.
(3)综合上表的统计量,请你对两名同学的得分进行评价并说明理由.
(4)为了取得更好的成绩,你认为在实验过程中还应该注意哪些方面
【详解答案】
1.C
2.B 解析:李林综合成绩为90×60%+80×40%=86(分).故选B.
3.B 解析:在这个问题中,最值得关注的是队伍的整齐,身高必须差不多,故应该关注该校所有女生身高的众数.故选B.
4.C
5.A 解析:由统计图可得,购买课外书花费100元的有20×10%=2(人),花费80元的有20×25%=5(人),花费50元的有20×40%=8(人),花费30元的有20×20%=4(人),花费20元的有20×5%=1(人),∴众数为50元,中位数为(50+50)÷2=50(元).故选A.
6.B 解析:把这组数据从小到大排列为91,92,94,95,95,95,96,
故中位数是95,故选项A说法正确,不符合题意;
平均数为×(91+92+94+95×3+96)=94,故选项D说法正确,不符合题意.
方差为×[(91-94)2+(92-94)2+(94-94)2+3×(95-94)2+(96-94)2]=,故选项B说法错误,符合题意;
众数是95,故选项C说法正确,不符合题意.故选B.
7.A 解析:∵这组数据的众数与平均数恰好相等,∴众数为9.∴9+9+x+8=9×4,∴x=10.故选A.
8.C 解析:由题表可知,年龄为15岁与年龄为16岁的频数之和为x+10-x=10,故该组数据的众数为14岁,中位数为=14(岁),即对于不同的x,关于年龄的统计量不会发生改变的是众数和中位数.故选C.
9.D 解析:甲班视力值分别为4.7,5.0,4.7,4.8,4.7,4.7,4.6,4.4;从小到大排列为4.4,4.6,4.7,4.7,4.7,4.7,4.8,5.0.众数为4.7,中位数为=4.7,平均数为×(4.4+4.6+4.7+4.7+4.7+4.7+4.8+5.0)=4.7,方差为×(0.32+0.12+0.12+0.32) =0.025.乙班视力值分别为4.8,4.7,4.7,5.0,4.6,4.5,4.9,4.4;从小到大排列为4.4,4.5,4.6,4.7,4.7,4.8,4.9,5.0.众数为4.7,中位数为=4.7,平均数为×(4.4+4.5+4.6+4.7+4.7+4.8+4.9+5.0)=4.7,方差为×(0.32+0.22+0.12+0.12+0.22+ 0.32)=0.035.
甲、乙班视力值的平均数、中位数、众数都相等,甲班视力值的方差小于乙班视力值的方差,故D选项正确.故选D.
10.A 解析:这些运动员成绩的平均数是×(1.50×2+1.60×3+1.65×2+1.70×3+1.75×4+1.80×1)≈1.67(m),
第8位同学的成绩是1.70 m,故中位数是1.70 m;
数据1.75出现的次数最多,故众数是1.75 m.
∴正确结论的是②③.故选A.
11.18 解析:平均数为=18(元).
12.89 解析:选手甲的最终得分为==89(分).
13.9 解析:根据条形统计图可知得9分的人数最多,即众数为9分.
14.4 解析:设数据x1,x2,…,xn的平均数为a,则数据x1+3,x2+3,…,xn+3的平均数为a+3.数据x1,x2,…,xn的方差为
[(x1-a)2+(x2-a)2+…+(xn-a)2]=4,则数据x1+3,x2+3,…,xn+3的方差为{[(x1+3)-(a+3)]2+[(x2+3)-(a+3)]2+…+[(xn+ 3)-(a+3)]2}=[(x1-a)2+(x2-a)2+…+(xn-a)2]=4.
15.7 解析:∵一组数据6,6,m,7,7,8的众数为7,
∴m=7,
∴这组数据从小到大排列为6,6,7,7,7,8,
∴这组数据的中位数是=7.
16.17或18 解析:因为中位数是4,最大的数是8,所以第二个数和第三个数的和是8.因为这四个数是不相等的正整数,所以这两个数是3,5或2,6,所以这四个数是1,3,5,8或2,3,5,8或1,2,6,8,所以这四个数的和为17或18.
17.解:(-7-10+9+2-1+5-8+10+4+9)÷10=1.3,
1.3+90=91.3(分).
答:他们的平均成绩是91.3分.
18.解:∵一组数据从小到大排列为1,2,3,x,4,5,这组数据的中位数为3,∴x=3,
∴这组数据的平均数是(1+2+3+3+4+5)÷6=3,
∴这组数据的方差是×[(1-3)2+(2-3)2+(3-3)2×2+(4-3)2+(5-3)2]=.
19.解:(1)小明一共调查的户数是1+1+3+6+4+2+2+1=20.
(2)∵在这组数据中,4出现了6次,出现的次数最多,
∴3月份用水量的众数是4 t.
∵将这组数据按从小到大的顺序排列,其中正中间两个数的平均数是=4,
∴3月份用水量的中位数是4 t.
3月份用水量的平均数是×(1×1+2×1+3×3+4×6+5×4+6×2+7×2+8×1)=4.5(t).
20.解:(1)2 2
(2)小红购买西红柿的平均价格为=(元/kg),
小慧购买西红柿的平均价格为=3(元/kg),
∵<3,
∴小红买的西红柿要便宜些.
21.解:甲、乙两人射击成绩的平均数分别为
=×(7×2+8×2+10×1)=8(环),
=×(7×1+8×3+9×1)=8(环).
甲、乙两人射击成绩的方差分别为
=×[2×(7-8)2+2×(8-8)2+(10-8)2]=1.2,
=×[(7-8)2+3×(8-8)2+(9-8)2]=0.4.
∵>,∴乙同学的射击成绩更稳定.
22.解:(1)由题意,得A地考生的数学平均分为×(90×3 000+80×2 000)=86(分).
(2)不能.举例如下:
如B地甲类学校有考生1 000人,乙类学校有考生3 000人,则B地考生的数学平均分为×(94×1 000+82×3 000)=85(分),
因为85<86,所以不能判断B地考生数学平均分一定比A地考生数学平均分高(答案不唯一,只要作出正确判断,并且所举的例子能说明该判断即可).
23.解:(1)∵(540+450+300×2+240×6+210×3+120×2)÷15=3 900÷15=260(件),
∴这15名工人该月加工零件数的平均数为260件.
∵15个数据按照从小到大的顺序排列,第8个是中位数,
∴中位数为240件.
∵240出现了6次,次数最多,∴众数是240件.
答:这15名工人该月加工的零件数的平均数是260件,中位数是240件,众数是240件.
(2)工作任务确定为260件不合理.理由:由题意,得每月能完成260件的人数是4,有11人不能完成此任务.尽管260件是平均数,但不利于调动工人的积极性,而240件既是中位数又是众数,故任务确定为240件较合理.
24.解:(1)八年级(1)班10名学生的平均数学成绩为
=×(50+55+95+80+90+85+100+100+85+60)=80(分),
八年级(2)班10名学生的平均数学成绩为
=×(85+75+70+95+100+90+65+70+80+70)=80(分).
(2)八年级(1)班10名学生数学成绩的方差为=×[(50-80)2+(55-80)2+(95-80)2+(80-80)2+(90-80)2+(85-80)2+ (100-80)2+(100-80)2+(85-80)2+(60-80)2]=310,八年级(2)班10名学生数学成绩的方差为=×[(85-80)2+(75-80)2+(70-80)2+(95-80)2+(100-80)2+(90-80)2+(65-80)2+(70-80)2+(80-80)2+(70-80)2]=130.
(3)由(1)(2)的计算可知八年级(1)班学生之间的数学成绩差异比八年级(2)班学生之间的数学成绩差异要大得多,因此八年级(1)班学生实施分层教学、因材施教的效果会更好.
25.解:(1)8分
(2)①8 8
②因为两个年级成绩的平均数、中位数相同,九年级成绩的众数比八年级大,九年级成绩的波动小,所以应该给九年级颁奖.
(3)八年级的获奖率为(10+7+11)÷50×100%=56%,
九年级的获奖率为(14+13+6)÷50×100%=66%,
因为66%>56%,所以九年级的获奖率高.
26.解:(1)8 8 9
(2)甲的方差较小,成绩比较稳定 乙的中位数是9,众数也是9,获奖的可能性较大
(3)不变 变小 变小
27.解:(1)2 >
(2)小海书写准确性得分的平均数b==2.
(3)①从操作规范性来分析,小青和小海得分的平均数相等,但是小海得分的方差小于小青得分的方差,所以小海在物理实验操作中发挥更稳定.
②从书写准确性来分析,小海得分的平均数比小青得分的平均数高,所以小海在物理实验中书写更准确.
③从两个方面综合分析,小海的操作更稳定,并且书写的准确性更高,所以小海的综合成绩更好.
(4)①熟悉实验方案和操作流程.
②注意仔细观察实验现象和结果.
③平稳心态,沉稳应对.
(第(3)(4)题答案不唯一,言之有理即可)
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.为增强学生的环保意识,共建绿色文明校园,某学校组织“废纸宝宝旅行记”活动.经统计,七年级5个班级一周回收废纸情况如下表:
班级 一班 二班 三班 四班 五班
废纸重量/kg 4.5 4.4 5.1 3.3 5.7
则每个班级回收废纸的平均重量为 ( )
A.5 kg B.4.8 kg C.4.6 kg D.4.5 kg
2.(2024南充中考)学校举行篮球技能大赛,评委从控球技能和投球技能两方面为选手打分,各项成绩均按百分制计,然后再按控球技能占60%,投球技能占40%计算选手的综合成绩(百分制).选手李林控球技能得90分,投球技能得80分.李林综合成绩为 ( )
A.170分 B.86分 C.85分 D.84分
3.某校运动会前夕,要选60名身高基本相同的女同学组成表演方阵,在这个问题中,最值得关注的是该校所有女生身高的 ( )
A.方差 B.众数 C.平均数 D.中位数
4.小张参加某节目的海选,共有17位选手参加角逐争取8个晋级名额,已知他们的分数互不相同,小张要判断自己是否能够晋级,只需知道这17名选手成绩统计量中的 ( )
A.平均数 B.众数 C.中位数 D.频数
5.小明调查了班级里20位同学本学期购买课外书的花费情况,并将结果绘制成了如图所示的统计图.这20位同学本学期购买课外书的花费的众数和中位数分别是 ( )
A.50元,50元 B.50元,30元 C.80元,50元 D.30元,50元
6.(2024广元中考)在五四文艺晚会节目评选中,某班选送的节目得分如下:91,96,95,92,94,95,95,分析这组数据,下列说法错误的是 ( )
A.中位数是95 B.方差是3
C.众数是95 D.平均数是94
7.某位同学四次射击测试成绩(单位:环)分别为:9,9,x,8,若这组数据的众数与平均数恰好相等,则x的值为 ( )
A.10 B.9 C.8 D.7
8.某校合唱团有30名成员,合唱团成员的年龄分布统计表如下:
年龄/岁 13 14 15 16
频数 5 15 x 10-x
则对于不同的x,下列关于年龄的统计量不会发生改变的是 ( )
A.平均数、中位数 B.平均数、方差
C.众数、中位数 D.众数、方差
9.长时间观看手机、电脑等电子产品对视力影响非常大.6月6日是“全国爱眼日”,为了解学生的视力情况,某学校从甲、乙两个班级各抽取8名学生进行调查,并将统计数据绘制成如图所示的折线统计图,则下列说法正确的是 ( )
A.甲班视力值的平均数大于乙班视力值的平均数
B.甲班视力值的中位数大于乙班视力值的中位数
C.甲班视力值的众数小于乙班视力值的众数
D.甲班视力值的方差小于乙班视力值的方差
10.(2024滨州中考)在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80
人数 2 3 2 3 4 1
某同学分析上表后得出如下结论:
①这些运动员成绩的平均数是1.65 m;
②这些运动员成绩的中位数是1.70 m;
③这些运动员成绩的众数是1.75 m.
上述结论中正确的是 ( )
A.②③ B.①③ C.①② D.①②③
二、填空题:本大题共6小题,每小题4分,共24分.
11.在“献爱心”捐款活动中,某校八年级一班同学人人拿出自己的零花钱,现将同学们的捐款数整理成统计表,则该班同学平均每人捐款 元.
捐款数/元 5 10 20 50
人数/人 4 15 6 5
12.某校开展主题为“我身边的共产党员”的演讲比赛.比赛从演讲内容、演讲技巧、演讲效果三个方面打分,最终得分按4∶3∶3的比例计算.若选手甲在演讲内容、演讲技巧、演讲效果三个方面的得分分别为95分、80分、90分,则选手甲的最终得分为 分.
13.(2024河南中考)2024年3月是第8个全国近视防控宣传教育月,其主题是“有效减少近视发生,共同守护光明未来”.某校组织各班围绕这个主题开展板报宣传活动,并对各班的宣传板报进行评分,得分情况如图,则得分的众数为 分.
14.如果一组数据x1,x2,…,xn的方差是4,那么另一组数据x1+3,x2+3,…,xn+3的方差是 .
15.(2024南充中考)若一组数据6,6,m,7,7,8的众数为7,则这组数据的中位数为 .
16.若四个互不相等的正整数中,最大的数是8,中位数是4,则这四个数的和为 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(7分)某班10名学生在一次数学测验中的成绩以90分为标准,超过的分数记为正数,不足的分数记为负数,如下:-7,-10,+9,+2,-1,+5,-8,+10,+4,+9.求他们的平均成绩.
18.(7分)一组数据从小到大排列为1,2,3,x,4,5,若这组数据的中位数为3,求这组数据的方差.
19.(8分)为了宣传节约用水,小强调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
(1)小明一共调查了多少户家庭
(2)求所调查家庭3月份用水量的众数、中位数和平均数.
20.(8分)假期里,小红和小慧去买菜,三次购买的西红柿价格和数量如表:
类别 单价/(元/kg) 合计
4 3 2
小红购买的数量/kg 1 2 3 6
小慧购买的数量/kg 2 2 2 6
(1)小红和小慧购买西红柿数量的中位数是 kg,众数是 kg.
(2)从平均价格看,谁买的西红柿要便宜些
21.(8分)甲、乙两名同学进行射击训练,在相同条件下各射靶5次,成绩统计如下:
命中环数 7 8 9 10
甲命中相应环数的次数 2 2 0 1
乙命中相应环数的次数 1 3 1 0
若从甲、乙两人射击成绩方差的角度评价两人的射击水平,则谁的射击成绩更稳定些
22.(8分)(2024福建中考)已知A、B两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有考生3 000人,数学平均分为90分;乙类学校有考生2 000人,数学平均分为80分.
(1)求A地考生的数学平均分.
(2)若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学平均分一定比A地考生数学平均分高 若能,请给予证明;若不能,请举例说明.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)某机械厂有15名工人,某月这15名工人加工的零件数统计如下:
人数 1 1 2 6 3 2
加工零件数/件 540 450 300 240 210 120
(1)求这15名工人该月加工的零件数的平均数、中位数和众数.
(2)假如部门负责人把每位工人每月加工零件的任务确定为260件,你认为是否合理 为什么 如果不合理,你认为多少较为合适
24.(8分)从某校八年级(1)班和(2)班的一次数学考试成绩中分别抽取10名学生的数学成绩进行分析,成绩(单位:分)如下:
(1)班:50,55,95,80,90,85,100,100,85,60.
(2)班:85,75,70,95,100,90,65,70,80,70.
(1)分别计算这两个班10名学生的平均数学成绩.
(2)分别计算这两个班10名学生数学成绩的方差.
(3)由以上数据,你认为哪一个班实施分层教学、因材施教的效果会更好
25.(10分)某校团委在八、九年级各抽取50名团员开展团知识竞赛活动,为便于统计成绩,制定了取整数的计分方式,满分10分.现将他们的竞赛成绩进行整理、分析,给出了下列图表:
年级 众数/分 中位数/分 方差
八年级 7 8 1.88
九年级 a b 1.56
(1)八年级的平均成绩是8分,九年级的平均成绩是 .
(2)请根据图表中的信息,回答下列问题.
①a= ,b= .
②现要给成绩突出的年级颁奖,你认为应该给哪个年级颁奖
(3)若规定成绩为10分的学生获一等奖,成绩为9分的学生获二等奖,成绩为8分的学生获三等奖,通过计算说明哪个年级的获奖率高.
26.(10分)某校八年级(1)班甲、乙两男生在5次引体向上测试中有效次数如下:甲:8,8,7,8,9;乙:5,9,7,10,9.甲、乙两同学引体向上的平均数、众数、中位数、方差如表:
学生 平均数 众数 中位数 方差
甲 8 b 8 0.4
乙 a 9 c 3.2
根据以上信息,回答下列问题:
(1)表格中a= , b= ,c= .(填数值)
(2)体育老师根据这5次的成绩,决定选择甲同学代表班级参加年级引体向上比赛,选择甲的理由是 .班主任李老师根据去年比赛的成绩(至少9次才能获奖) ,决定选择乙同学代表班级参加年级引体向上比赛,选择乙的理由是 .
(3)如果乙同学再做一次引体向上,有效次数为8,那么乙同学6次引体向上成绩的平均数 ,中位数 ,方差 . (填“变大”“变小”或“不变”)
27.(14分)(2024青海中考)为了解学生物理实验操作情况,抽取小青和小海两名同学的10次实验得分,并对他们的得分情况从以下两方面整理描述如下:
①操作规范性:
②书写准确性:
小青:1 1 2 2 2 3 1 3 2 1
小海:1 2 2 3 3 3 2 1 2 1
操作规范性和书写准确性的得分统计表:
学生 操作规范性 书写准确性
平均数 方差 平均数 中位数
小青 4 1.8 a
小海 4 b 2
根据以上信息,回答下列问题:
(1)表格中的a= ,比较和的大小 .
(2)计算表格中b的值.
(3)综合上表的统计量,请你对两名同学的得分进行评价并说明理由.
(4)为了取得更好的成绩,你认为在实验过程中还应该注意哪些方面
【详解答案】
1.C
2.B 解析:李林综合成绩为90×60%+80×40%=86(分).故选B.
3.B 解析:在这个问题中,最值得关注的是队伍的整齐,身高必须差不多,故应该关注该校所有女生身高的众数.故选B.
4.C
5.A 解析:由统计图可得,购买课外书花费100元的有20×10%=2(人),花费80元的有20×25%=5(人),花费50元的有20×40%=8(人),花费30元的有20×20%=4(人),花费20元的有20×5%=1(人),∴众数为50元,中位数为(50+50)÷2=50(元).故选A.
6.B 解析:把这组数据从小到大排列为91,92,94,95,95,95,96,
故中位数是95,故选项A说法正确,不符合题意;
平均数为×(91+92+94+95×3+96)=94,故选项D说法正确,不符合题意.
方差为×[(91-94)2+(92-94)2+(94-94)2+3×(95-94)2+(96-94)2]=,故选项B说法错误,符合题意;
众数是95,故选项C说法正确,不符合题意.故选B.
7.A 解析:∵这组数据的众数与平均数恰好相等,∴众数为9.∴9+9+x+8=9×4,∴x=10.故选A.
8.C 解析:由题表可知,年龄为15岁与年龄为16岁的频数之和为x+10-x=10,故该组数据的众数为14岁,中位数为=14(岁),即对于不同的x,关于年龄的统计量不会发生改变的是众数和中位数.故选C.
9.D 解析:甲班视力值分别为4.7,5.0,4.7,4.8,4.7,4.7,4.6,4.4;从小到大排列为4.4,4.6,4.7,4.7,4.7,4.7,4.8,5.0.众数为4.7,中位数为=4.7,平均数为×(4.4+4.6+4.7+4.7+4.7+4.7+4.8+5.0)=4.7,方差为×(0.32+0.12+0.12+0.32) =0.025.乙班视力值分别为4.8,4.7,4.7,5.0,4.6,4.5,4.9,4.4;从小到大排列为4.4,4.5,4.6,4.7,4.7,4.8,4.9,5.0.众数为4.7,中位数为=4.7,平均数为×(4.4+4.5+4.6+4.7+4.7+4.8+4.9+5.0)=4.7,方差为×(0.32+0.22+0.12+0.12+0.22+ 0.32)=0.035.
甲、乙班视力值的平均数、中位数、众数都相等,甲班视力值的方差小于乙班视力值的方差,故D选项正确.故选D.
10.A 解析:这些运动员成绩的平均数是×(1.50×2+1.60×3+1.65×2+1.70×3+1.75×4+1.80×1)≈1.67(m),
第8位同学的成绩是1.70 m,故中位数是1.70 m;
数据1.75出现的次数最多,故众数是1.75 m.
∴正确结论的是②③.故选A.
11.18 解析:平均数为=18(元).
12.89 解析:选手甲的最终得分为==89(分).
13.9 解析:根据条形统计图可知得9分的人数最多,即众数为9分.
14.4 解析:设数据x1,x2,…,xn的平均数为a,则数据x1+3,x2+3,…,xn+3的平均数为a+3.数据x1,x2,…,xn的方差为
[(x1-a)2+(x2-a)2+…+(xn-a)2]=4,则数据x1+3,x2+3,…,xn+3的方差为{[(x1+3)-(a+3)]2+[(x2+3)-(a+3)]2+…+[(xn+ 3)-(a+3)]2}=[(x1-a)2+(x2-a)2+…+(xn-a)2]=4.
15.7 解析:∵一组数据6,6,m,7,7,8的众数为7,
∴m=7,
∴这组数据从小到大排列为6,6,7,7,7,8,
∴这组数据的中位数是=7.
16.17或18 解析:因为中位数是4,最大的数是8,所以第二个数和第三个数的和是8.因为这四个数是不相等的正整数,所以这两个数是3,5或2,6,所以这四个数是1,3,5,8或2,3,5,8或1,2,6,8,所以这四个数的和为17或18.
17.解:(-7-10+9+2-1+5-8+10+4+9)÷10=1.3,
1.3+90=91.3(分).
答:他们的平均成绩是91.3分.
18.解:∵一组数据从小到大排列为1,2,3,x,4,5,这组数据的中位数为3,∴x=3,
∴这组数据的平均数是(1+2+3+3+4+5)÷6=3,
∴这组数据的方差是×[(1-3)2+(2-3)2+(3-3)2×2+(4-3)2+(5-3)2]=.
19.解:(1)小明一共调查的户数是1+1+3+6+4+2+2+1=20.
(2)∵在这组数据中,4出现了6次,出现的次数最多,
∴3月份用水量的众数是4 t.
∵将这组数据按从小到大的顺序排列,其中正中间两个数的平均数是=4,
∴3月份用水量的中位数是4 t.
3月份用水量的平均数是×(1×1+2×1+3×3+4×6+5×4+6×2+7×2+8×1)=4.5(t).
20.解:(1)2 2
(2)小红购买西红柿的平均价格为=(元/kg),
小慧购买西红柿的平均价格为=3(元/kg),
∵<3,
∴小红买的西红柿要便宜些.
21.解:甲、乙两人射击成绩的平均数分别为
=×(7×2+8×2+10×1)=8(环),
=×(7×1+8×3+9×1)=8(环).
甲、乙两人射击成绩的方差分别为
=×[2×(7-8)2+2×(8-8)2+(10-8)2]=1.2,
=×[(7-8)2+3×(8-8)2+(9-8)2]=0.4.
∵>,∴乙同学的射击成绩更稳定.
22.解:(1)由题意,得A地考生的数学平均分为×(90×3 000+80×2 000)=86(分).
(2)不能.举例如下:
如B地甲类学校有考生1 000人,乙类学校有考生3 000人,则B地考生的数学平均分为×(94×1 000+82×3 000)=85(分),
因为85<86,所以不能判断B地考生数学平均分一定比A地考生数学平均分高(答案不唯一,只要作出正确判断,并且所举的例子能说明该判断即可).
23.解:(1)∵(540+450+300×2+240×6+210×3+120×2)÷15=3 900÷15=260(件),
∴这15名工人该月加工零件数的平均数为260件.
∵15个数据按照从小到大的顺序排列,第8个是中位数,
∴中位数为240件.
∵240出现了6次,次数最多,∴众数是240件.
答:这15名工人该月加工的零件数的平均数是260件,中位数是240件,众数是240件.
(2)工作任务确定为260件不合理.理由:由题意,得每月能完成260件的人数是4,有11人不能完成此任务.尽管260件是平均数,但不利于调动工人的积极性,而240件既是中位数又是众数,故任务确定为240件较合理.
24.解:(1)八年级(1)班10名学生的平均数学成绩为
=×(50+55+95+80+90+85+100+100+85+60)=80(分),
八年级(2)班10名学生的平均数学成绩为
=×(85+75+70+95+100+90+65+70+80+70)=80(分).
(2)八年级(1)班10名学生数学成绩的方差为=×[(50-80)2+(55-80)2+(95-80)2+(80-80)2+(90-80)2+(85-80)2+ (100-80)2+(100-80)2+(85-80)2+(60-80)2]=310,八年级(2)班10名学生数学成绩的方差为=×[(85-80)2+(75-80)2+(70-80)2+(95-80)2+(100-80)2+(90-80)2+(65-80)2+(70-80)2+(80-80)2+(70-80)2]=130.
(3)由(1)(2)的计算可知八年级(1)班学生之间的数学成绩差异比八年级(2)班学生之间的数学成绩差异要大得多,因此八年级(1)班学生实施分层教学、因材施教的效果会更好.
25.解:(1)8分
(2)①8 8
②因为两个年级成绩的平均数、中位数相同,九年级成绩的众数比八年级大,九年级成绩的波动小,所以应该给九年级颁奖.
(3)八年级的获奖率为(10+7+11)÷50×100%=56%,
九年级的获奖率为(14+13+6)÷50×100%=66%,
因为66%>56%,所以九年级的获奖率高.
26.解:(1)8 8 9
(2)甲的方差较小,成绩比较稳定 乙的中位数是9,众数也是9,获奖的可能性较大
(3)不变 变小 变小
27.解:(1)2 >
(2)小海书写准确性得分的平均数b==2.
(3)①从操作规范性来分析,小青和小海得分的平均数相等,但是小海得分的方差小于小青得分的方差,所以小海在物理实验操作中发挥更稳定.
②从书写准确性来分析,小海得分的平均数比小青得分的平均数高,所以小海在物理实验中书写更准确.
③从两个方面综合分析,小海的操作更稳定,并且书写的准确性更高,所以小海的综合成绩更好.
(4)①熟悉实验方案和操作流程.
②注意仔细观察实验现象和结果.
③平稳心态,沉稳应对.
(第(3)(4)题答案不唯一,言之有理即可)
