第二学期期末评估测试卷(B) (含答案)2024-2025学年数学华东师大版八年级下册
文档属性
| 名称 | 第二学期期末评估测试卷(B) (含答案)2024-2025学年数学华东师大版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 218.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 14:10:02 | ||
图片预览




文档简介
第二学期期末评估测试卷(B)
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.已知1 nm=10-9 m,则28 nm用科学记数法表示是 ( )
A.28×10-9 m B.2.8×10-9 m
C.2.8×10-8 m D.2.8×10-10 m
2.要使分式有意义,则x的取值范围是 ( )
A.x≠-1 B.x>-1 C.x<-1 D.x≠1
3.若y=kx-9 的函数值y随x的增大而减小,则k的值可能是下列的 ( )
A.4 B.-3 C.0 D.
4.如图,在 ABCD 中,连结 AC,∠ABC=∠CAD,AB=2,则AC的长是 ( )
A. B.2 C.2 D.4
5.如图所示,在矩形ABCD中,AB>AD,AC与BD相交于点O,下列说法正确的是 ( )
A.点O为矩形ABCD的对称中心
B.点O为线段AB的对称中心
C.直线BD为矩形ABCD的对称轴
D.直线AC为线段BD的对称轴
6.(2024宜宾中考)某校为了解九年级学生在校的锻炼情况,抽取10名学生,记录他们某一天在校的锻炼时间(单位:min):65,67,75,65,75,80,75,88,78,80.对这组数据判断正确的是 ( )
A.方差为0 B.众数为75
C.中位数为77.5 D.平均数为75
7.已知直线y=kx-4(k<0)与两坐标轴所围成的三角形面积等于4,则直线的表达式为 ( )
A.y=-x-4 B.y=-2x-4
C.y=-3x+4 D.y=-3x-4
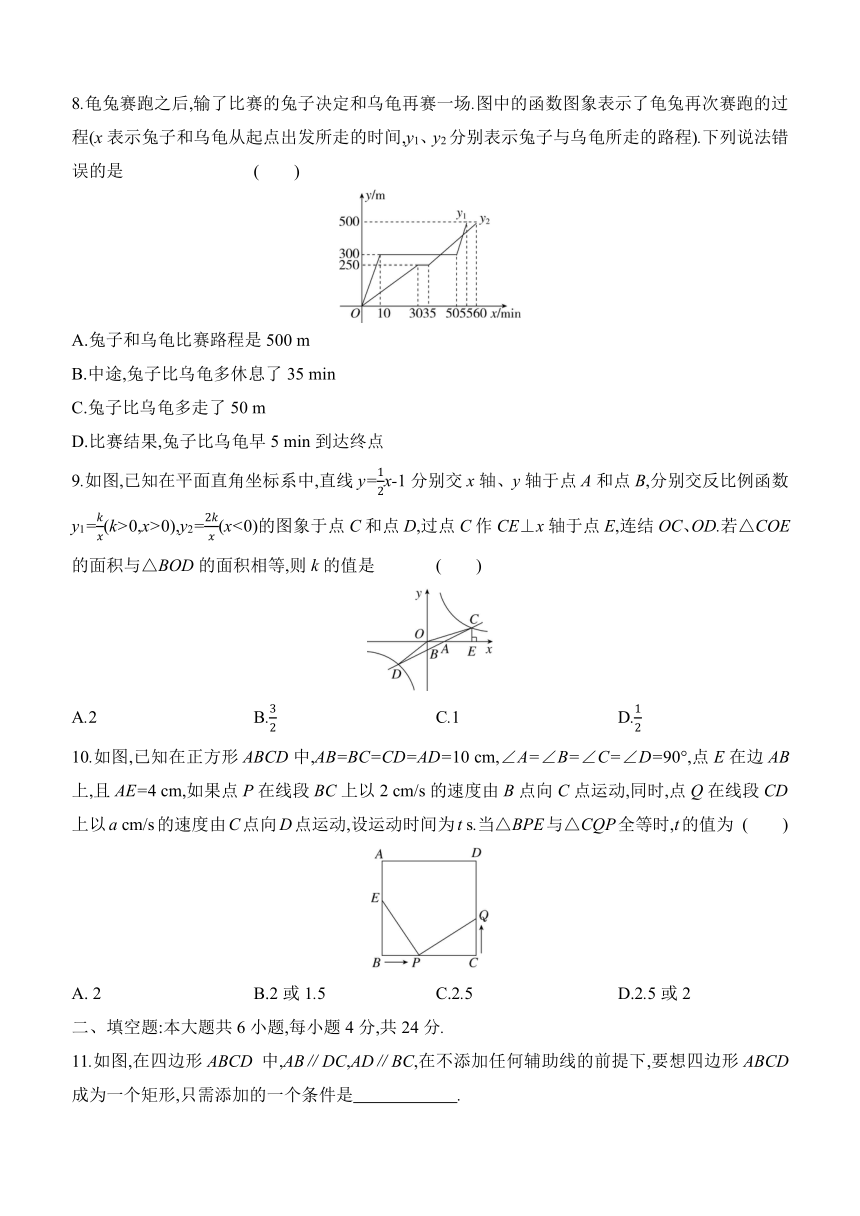
8.龟兔赛跑之后,输了比赛的兔子决定和乌龟再赛一场.图中的函数图象表示了龟兔再次赛跑的过程(x表示兔子和乌龟从起点出发所走的时间,y1、y2分别表示兔子与乌龟所走的路程).下列说法错误的是 ( )
A.兔子和乌龟比赛路程是500 m
B.中途,兔子比乌龟多休息了35 min
C.兔子比乌龟多走了50 m
D.比赛结果,兔子比乌龟早5 min到达终点
9.如图,已知在平面直角坐标系中,直线y=x-1分别交x轴、y轴于点A和点B,分别交反比例函数y1=(k>0,x>0),y2=(x<0)的图象于点C和点D,过点C作CE⊥x轴于点E,连结OC、OD.若△COE的面积与△BOD的面积相等,则k的值是 ( )
A.2 B. C.1 D.
10.如图,已知在正方形ABCD中,AB=BC=CD=AD=10 cm,∠A=∠B=∠C=∠D=90°,点E在边AB上,且AE=4 cm,如果点P在线段BC上以2 cm/s的速度由B点向C点运动,同时,点Q在线段CD上以a cm/s的速度由C点向D点运动,设运动时间为t s.当△BPE与△CQP全等时,t的值为 ( )
A. 2 B.2或1.5 C.2.5 D.2.5或2
二、填空题:本大题共6小题,每小题4分,共24分.
11.如图,在四边形ABCD 中,AB∥DC,AD∥BC,在不添加任何辅助线的前提下,要想四边形ABCD成为一个矩形,只需添加的一个条件是 .
12.(2024绥化中考)化简:÷= .
13.某同学对某地区某月连续六天的最高气温做了记录,每天最高气温与25 ℃的上下波动数据分别为+3,-4,-3,+7,+3,0,则这六天中气温波动数据的方差为 .
14.已知 ABCD中,AC、BD交于点O,若AB=6,AC=8,则BD的取值范围是 .
15.如图,一个正比例函数图象与一次函数y=-x+1的图象相交于点P,则这个正比例函数的表达式是 .
16.如图,在矩形ABCD中,AD=4,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则四边形ABCE的面积为 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(7分)先化简,再求值:
÷,其中a满足a2+2a-15=0.
18.(7分)A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30 kg,A型机器人搬运900 kg所用时间与B型机器人搬运600 kg所用时间相等,两种机器人每小时分别搬运多少千克化工原料
19.(8分)课本再现
思考 “对角线互相垂直”是菱形所特有的性质.那么从对角线的角度,你可以得到关于菱形判定的什么猜想 可以发现并证明菱形的一个判定定理:对角线互相垂直的平行四边形是菱形.
(1)定理证明:为了证明该定理,小明同学画出了图形(如图1),并写出了“已知”和“求证”,请你完成证明过程.
已知:在 ABCD中,对角线BD⊥AC,垂足为O.
求证: ABCD是菱形.
(2)知识应用:如图2,在 ABCD中,对角线AC和BD相交于点O,AD=5,AC=8,BD=6.求证: ABCD是菱形.
20.(8分)已知y是x的一次函数,且当x=2时,y=4,当x=-1时,y=1.
(1)求这个一次函数的表达式.
(2)若点(-2,m),(3,n)在该一次函数的图象上,比较m、n的大小.
21.(8分)(2024湖南中考)如图,在四边形ABCD中,AB∥CD,点E在边AB上, .
请从“①∠B=∠AED;②AE=BE,AE=CD”这两组条件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
(1)求证:四边形BCDE为平行四边形.
(2)若AD⊥AB,AD=8,BC=10,求线段AE的长.
22.(8分)如图,在平面直角坐标系中,一次函数y=k1x+b(k1≠0)的图象与反比例函数y=(k2≠0)的图象相交于A(3,4)、B(-4,m)两点.
(1)求一次函数和反比例函数的表达式.
(2)若点D在x轴上,位于原点右侧,且OA=OD,求△AOD的面积.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(10分)(2024河北中考)某公司为提高员工的专业能力,定期对员工进行技能测试.考虑多种因素影响,需将测试的原始成绩x(分)换算为报告成绩y(分).已知原始成绩满分150分,报告成绩满分100分,换算规则如下:
当0≤x当p≤x<150时,y=+80.
(其中p是小于150的常数,是原始成绩的合格分数线,80是报告成绩的合格分数线)公司规定报告成绩为80分及80分以上(即原始成绩为p及p以上)为合格.
(1)甲、乙的原始成绩分别为95分和130分,若p=100,求甲、乙的报告成绩.
(2)丙、丁的报告成绩分别为92分和64分,若丙的原始成绩比丁的原始成绩高40分,请推算p的值.
(3)下表是该公司100名员工某次测试的原始成绩统计表:
原始 成绩/分 95 100 105 110 115 120 125 130 135 140 145 150
人数 1 2 2 5 8 10 7 16 20 15 9 5
①直接写出这100名员工原始成绩的中位数;
②若①中的中位数换算成报告成绩为90分,直接写出该公司此次测试的合格率.
24.(10分)如图,在△ABC中,D是BC的中点,F、E分别是AD及其延长线上的点,CF∥BE,连结BF、CE.
(1)求证:四边形BECF是平行四边形.
(2)①若AB=5,则AC 的长为 时,四边形BECF是菱形;
②若 AB=5,BC=6,且四边形BECF是正方形,求AF的长.
25.(10分)为了燃气使用安全,某燃气公司要求所有用户必须安装燃气报警器,当空气中的燃气浓度达到一定量时,报警系统就会报警并切断燃气阀门以保证安全,检测人员用标准天然气气瓶检测燃气报警器的有效性时,每分钟记录一次空气中的燃气浓度,下表记录了连续5 min内6个时间点的燃气浓度.
时间/min 0 1 2 3 4 5
燃气浓度/% 0 3 6 9 12 15
【探索发现】
(1)建立如图所示的平面直角坐标系,横轴表示检测时间x(min),纵轴表示空气中的燃气浓度y(%),图中已经描出以表格中数据为坐标的部分点,请你将表格中剩余的点描出.
(2)观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式;如果不在同一条直线上,请说明理由.
【结论应用】
若按这种上涨规律,当浓度达到24%时,报警系统会自动发出警报,当浓度达到50%时,会自动切断燃气阀门.
(3)预测第 min时,系统会发出警报.
(4)报警后,若无人发现,再过 min系统会自动切断燃气阀门.
26.(10分)如图,在平面直角坐标系中,四边形OABC是矩形,反比例函数y=(x>0)的图象分别与AB、BC交于点D(4,1)和点E,且点D为AB的中点.
(1)求反比例函数的表达式和点E的坐标.
(2)若一次函数y=x+m与反比例函数y=(x>0)的图象相交于点M,当点M在反比例函数图象上D、E之间的部分时(点M可与点D、E重合),直接写出m的取值范围.
27.(10分)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元,今年该型号自行车每辆售价预计比去年降低200元,若该型号自行车的销售数量与去年相同,则今年的销售总额将比去年减少10%.
(1)A型自行车去年每辆售价为多少元
(2)该车行今年计划新进一批A型自行车和新款B型自行车共60辆,且B型自行车的进货数量不超过A型自行车数量的2倍,已知A型自行车和B型自行车的进货价格分别为1 500元和1 800元,计划B型自行车销售价格为2 400元,应如何进货才能使这批自行车获利最多
【详解答案】
1.C 解析:∵1 nm=10-9 m,∴28 nm=28×10-9 m=2.8×10-8 m.故选C.
2.A 3.B 4.B
5.A 解析:矩形ABCD是中心对称图形,对称中心是对角线的交点,故A符合题意;线段AB的对称中心是线段AB的中点,故B不符合题意;矩形ABCD是轴对称图形,对称轴是过一组对边中点的直线,故C不符合题意;过线段BD的中点的垂线是线段BD的对称轴,故D不符合题意.故选A.
6.B 解析:65,67,75,65,75,80,75,88,78,80中,
平均数为×(65+67+75+65+75+80+75+88+78+80)=74.8,
65,67,75,65,75,80,75,88,78,80按从小到大的顺序排列为65,65,67,75,75,75,78,80,80,88,
∴中位数为=75,众数为75,
方差为×[(65-74.8)2×2+(67-74.8)2+(75-74.8)2×3+(78-74.8)2+(80-74.8)2×2+(88-74.8)2]=49.16.故选B.
7.B 解析:直线y=kx-4(k<0)与两坐标轴的交点坐标为(0,-4),,∵直线y=kx-4(k<0)与两坐标轴所围成的三角形面积等于4,∴|-4|××=4,解得k=-2,则直线的表达式为y=-2x-4.故选B.
8.C 解析:A.“龟兔再次赛跑”的路程为500 m,原说法正确,故此选项不符合题意;B.乌龟在途中休息了35-30=5(min),兔子在途中休息了50-10=40(min),兔子比乌龟多休息了35 min,原说法正确,故此选项不符合题意;C.兔子和乌龟同时从起点出发,都走了500 m,原说法错误,故此选项符合题意;D.比赛结果,兔子比乌龟早5 min到达终点,原说法正确,故此选项不符合题意.故选C.
9.A 解析:由题意可知B(0,-1),
∵直线y=x-1与y1=交于点C,
∴S△OCE=k.
设D,
∴S△BOD=×1×(-x)=-x.
∵△COE的面积与△BOD的面积相等,
∴k=-x.∴k=-x.
∴D(-k,-2).
∵D点在直线y=x-1上,
∴-2=-k-1.∴k=2.故选A.
10.D 解析:当a=2,即点Q的运动速度与点P的运动速度都是2 cm/s时,若△BPE≌△CQP,则BP=CQ,BE=CP.∵AB=BC=10 cm,AE=4 cm,∴BE=CP=6 cm,∴BP=10-6=4(cm),∴运动时间=4÷2=2(s).当a≠2,即点Q的运动速度与点P的运动速度不相等时,∴BP≠CQ.∵∠B=∠C=90°,∴要使△BPE与△CQP全等,只要BP=PC=5 cm,CQ=BE=6 cm,∴点P、Q运动的时间t==2.5(s).故选D.
11.∠A=90°(答案不唯一)
12. 解析:原式=÷=·=.
13. 解析:数据的平均数=×(3-4-3+7+3+0)=1,方差s2=×[(3-1)2+(-4-1)2+(-3-1)2+(7-1)2+(3-1)2+(0-1)2]=.
14.4∴415.y=-2x 解析:∵正比例函数图象与一次函数y=-x+1的图象相交于点P,P点的纵坐标为2,∴2=-x+1,解得x=-1.∴点P的坐标为(-1,2).设正比例函数的表达式为y=kx(k≠0),∴2=-k,解得k=-2.∴正比例函数的表达式为y=-2x.
16.4-8 解析:由题意可知,BC=EF=AD=4,AE=AB,
∵DE=EF=4,
∴AE=AB==,
∴S四边形ABCE=S矩形ABCD-S△ADE=AB·AD-AD·DE=×4-×4×4=4-8.
17.解:原式=·
=·
=·
=.
∵a2+2a-15=0,∴a2+2a=15,
∴原式=.
18.解:设B型机器人每小时搬运x kg化工原料,则A型机器人每小时搬运(x+30)kg化工原料,
根据题意,得=,解得x=60,
经检验,x=60是原方程的解,且符合题意,
∴x+30=60+30=90.
答:A型机器人每小时搬运90 kg化工原料,B型机器人每小时搬运60 kg化工原料.
19.证明:(1)∵四边形ABCD是平行四边形,
∴AO=CO,AB=DC.
∵BD⊥AC,
∴∠AOB=∠COB=90°.
在△AOB和△COB中,
∴△AOB≌△COB(S.A.S.).
∴AB=CB.
同理可得△DOA≌△DOC(S.A.S.),则DA=DC,
又∵AB=CD,
∴AB=BC=CD=DA.
∴ ABCD是菱形.
(2)∵四边形ABCD是平行四边形,AD=5,AC=8,BD=6.
∴DO=BO=BD=3,AO=CO=AC=4.
在△AOD中,AD2=25,AO2+OD2=42+32=25,
∴AD2=AO2+OD2.
∴△AOD是直角三角形,且∠AOD=90°.
∴AC⊥BD.
∴ ABCD是菱形.
20.解:(1)设一次函数的表达式为y=kx+b,
把x=2,y=4;x=-1,y=1分别代入得
解得
所以一次函数的表达式为y=x+2.
(2)把(-2,m)代入y=x+2得m=-2+2=0,
把点(3,n)代入y=x+2得n=3+2=5,
所以m21.解:(1)①
证明:∵∠B=∠AED,∴BC∥DE,
∵AB∥CD,
∴四边形BCDE为平行四边形.
②
证明:∵AE=BE,AE=CD,
∴BE=CD,
∵AB∥CD,
∴四边形BCDE为平行四边形.
(答案不唯一,任选其一即可)
(2)由(1)可知,四边形BCDE为平行四边形,∴DE=BC=10,
∵AD⊥AB,∴∠A=90°,
∴AE===6,即线段AE的长为6.
22.解:(1)∵反比例函数y=(k2≠0)的图象与一次函数y=k1x+b(k1≠0)的图象相交于点A(3,4)、B(-4,m),
∴4=.∴k2=12.
∴反比例函数的表达式为y=.
∴m==-3.
∴点B的坐标为(-4,-3).
∴解得
∴一次函数的表达式为y=x+1.
(2)∵A(3,4),∴OA==5.
∵OA=OD,∴OD=5.
∴△AOD的面积=×5×4=10.
23.解:(1)当p=100时,甲的报告成绩为y==76 (分),
乙的报告成绩为
y=+80=92(分).
(2)∵92>80,∴当y=92时,+80=92,得x丙=90+p.
∵64<80,∴当y=64时,=64,得x丁=p.
∵x丙-x丁=40,∴90+p-p=40.
解得p=125.
(3)①中位数为130分.
②合格率为95%.
解法提示:①共计100名员工,且原始成绩已经从小到大排列好,
∴中位数是第50,51名员工原始成绩的平均数,
由表格得第50,51名员工原始成绩都是130分,
∴中位数为130分.
②当p>130时,则90=,
解得p=<130,故不成立,舍去;
当p≤130时,
则90=+80,
解得p=110,符合题意.
∴由表格得到原始成绩为110分及110分以上的人数为100-(1+2+2)=95,
∴合格率为×100%=95%.
24.解:(1)证明:∵D是BC的中点,
∴BD=CD,∴CF∥BE,
∴∠CFD=∠BED,
在△CFD和△BED中,
∴△CFD≌△BED(A.A.S.),
∴CF=BE,
∴四边形BECF是平行四边形.
(2)①5
②∵四边形BECF是正方形,
∴EF=BC=6,EF⊥BC,
∵D是BC的中点,
∴BD=CD=DF=DE=3,
∴AD===4,
∴AF=AD-DF=4-3=1.
25.解:(1)描点如图:
(2)观察可知它们在同一条直线上,
设直线所对应的函数表达式为y=kx+b(k≠0),
将点(0,0),(1,3)代入得
解得∴这条直线所对应的函数表达式为y=3x.
(3)8
(4)
26.解:(1)把(4,1)代人y=,得1=,解得k=4,
∴反比例函数的表达式为y=.
∵点A在x轴上,点D的纵坐标为1,D为AB的中点,
∴点B的纵坐标为2.
又∵四边形OABC为矩形,∴BE∥x轴,∴点E的纵坐标为2.
设点E的横坐标为a,则2=,解得a=2,
∴点E的坐标为(2,2).
(2)-3≤m≤0.
解法提示:当点M与点D重合时,
把(4,1)代入y=x+m,得1=4+m,解得m=-3.
当点M与点E重合时,
把(2,2)代入y=x+m,得2=2+m,解得m=0.
∴m的取值范围为-3≤m≤0.
27.解:(1)设A型自行车去年每辆售价为x元,则今年每辆售价为(x-200)元,
由题意,得=,
解得x=2 000.经检验,x=2 000是原方程的解,且符合题意.
答:A型自行车去年每辆售价为2 000元.
(2)设今年新进A型自行车a辆,则新进B型自行车(60-a)辆,获利y元.
由题意,得y=(1 800-1 500)a+(2 400-1 800)(60-a)=-300a+36 000.
∵B型自行车的进货数量不超过A型自行车数量的2倍,
∴60-a≤2a.∴a≥20.
∵y=-300a+36 000,-300<0,
∴y随a的增大而减少,∴当a=20时,y最大.
此时B型自行车进货数量为60-20=40(辆).
答:当新进A型自行车20辆,B型自行车 40辆时,才能使这批自行车获利最多.
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.已知1 nm=10-9 m,则28 nm用科学记数法表示是 ( )
A.28×10-9 m B.2.8×10-9 m
C.2.8×10-8 m D.2.8×10-10 m
2.要使分式有意义,则x的取值范围是 ( )
A.x≠-1 B.x>-1 C.x<-1 D.x≠1
3.若y=kx-9 的函数值y随x的增大而减小,则k的值可能是下列的 ( )
A.4 B.-3 C.0 D.
4.如图,在 ABCD 中,连结 AC,∠ABC=∠CAD,AB=2,则AC的长是 ( )
A. B.2 C.2 D.4
5.如图所示,在矩形ABCD中,AB>AD,AC与BD相交于点O,下列说法正确的是 ( )
A.点O为矩形ABCD的对称中心
B.点O为线段AB的对称中心
C.直线BD为矩形ABCD的对称轴
D.直线AC为线段BD的对称轴
6.(2024宜宾中考)某校为了解九年级学生在校的锻炼情况,抽取10名学生,记录他们某一天在校的锻炼时间(单位:min):65,67,75,65,75,80,75,88,78,80.对这组数据判断正确的是 ( )
A.方差为0 B.众数为75
C.中位数为77.5 D.平均数为75
7.已知直线y=kx-4(k<0)与两坐标轴所围成的三角形面积等于4,则直线的表达式为 ( )
A.y=-x-4 B.y=-2x-4
C.y=-3x+4 D.y=-3x-4
8.龟兔赛跑之后,输了比赛的兔子决定和乌龟再赛一场.图中的函数图象表示了龟兔再次赛跑的过程(x表示兔子和乌龟从起点出发所走的时间,y1、y2分别表示兔子与乌龟所走的路程).下列说法错误的是 ( )
A.兔子和乌龟比赛路程是500 m
B.中途,兔子比乌龟多休息了35 min
C.兔子比乌龟多走了50 m
D.比赛结果,兔子比乌龟早5 min到达终点
9.如图,已知在平面直角坐标系中,直线y=x-1分别交x轴、y轴于点A和点B,分别交反比例函数y1=(k>0,x>0),y2=(x<0)的图象于点C和点D,过点C作CE⊥x轴于点E,连结OC、OD.若△COE的面积与△BOD的面积相等,则k的值是 ( )
A.2 B. C.1 D.
10.如图,已知在正方形ABCD中,AB=BC=CD=AD=10 cm,∠A=∠B=∠C=∠D=90°,点E在边AB上,且AE=4 cm,如果点P在线段BC上以2 cm/s的速度由B点向C点运动,同时,点Q在线段CD上以a cm/s的速度由C点向D点运动,设运动时间为t s.当△BPE与△CQP全等时,t的值为 ( )
A. 2 B.2或1.5 C.2.5 D.2.5或2
二、填空题:本大题共6小题,每小题4分,共24分.
11.如图,在四边形ABCD 中,AB∥DC,AD∥BC,在不添加任何辅助线的前提下,要想四边形ABCD成为一个矩形,只需添加的一个条件是 .
12.(2024绥化中考)化简:÷= .
13.某同学对某地区某月连续六天的最高气温做了记录,每天最高气温与25 ℃的上下波动数据分别为+3,-4,-3,+7,+3,0,则这六天中气温波动数据的方差为 .
14.已知 ABCD中,AC、BD交于点O,若AB=6,AC=8,则BD的取值范围是 .
15.如图,一个正比例函数图象与一次函数y=-x+1的图象相交于点P,则这个正比例函数的表达式是 .
16.如图,在矩形ABCD中,AD=4,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则四边形ABCE的面积为 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(7分)先化简,再求值:
÷,其中a满足a2+2a-15=0.
18.(7分)A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30 kg,A型机器人搬运900 kg所用时间与B型机器人搬运600 kg所用时间相等,两种机器人每小时分别搬运多少千克化工原料
19.(8分)课本再现
思考 “对角线互相垂直”是菱形所特有的性质.那么从对角线的角度,你可以得到关于菱形判定的什么猜想 可以发现并证明菱形的一个判定定理:对角线互相垂直的平行四边形是菱形.
(1)定理证明:为了证明该定理,小明同学画出了图形(如图1),并写出了“已知”和“求证”,请你完成证明过程.
已知:在 ABCD中,对角线BD⊥AC,垂足为O.
求证: ABCD是菱形.
(2)知识应用:如图2,在 ABCD中,对角线AC和BD相交于点O,AD=5,AC=8,BD=6.求证: ABCD是菱形.
20.(8分)已知y是x的一次函数,且当x=2时,y=4,当x=-1时,y=1.
(1)求这个一次函数的表达式.
(2)若点(-2,m),(3,n)在该一次函数的图象上,比较m、n的大小.
21.(8分)(2024湖南中考)如图,在四边形ABCD中,AB∥CD,点E在边AB上, .
请从“①∠B=∠AED;②AE=BE,AE=CD”这两组条件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
(1)求证:四边形BCDE为平行四边形.
(2)若AD⊥AB,AD=8,BC=10,求线段AE的长.
22.(8分)如图,在平面直角坐标系中,一次函数y=k1x+b(k1≠0)的图象与反比例函数y=(k2≠0)的图象相交于A(3,4)、B(-4,m)两点.
(1)求一次函数和反比例函数的表达式.
(2)若点D在x轴上,位于原点右侧,且OA=OD,求△AOD的面积.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(10分)(2024河北中考)某公司为提高员工的专业能力,定期对员工进行技能测试.考虑多种因素影响,需将测试的原始成绩x(分)换算为报告成绩y(分).已知原始成绩满分150分,报告成绩满分100分,换算规则如下:
当0≤x
(其中p是小于150的常数,是原始成绩的合格分数线,80是报告成绩的合格分数线)公司规定报告成绩为80分及80分以上(即原始成绩为p及p以上)为合格.
(1)甲、乙的原始成绩分别为95分和130分,若p=100,求甲、乙的报告成绩.
(2)丙、丁的报告成绩分别为92分和64分,若丙的原始成绩比丁的原始成绩高40分,请推算p的值.
(3)下表是该公司100名员工某次测试的原始成绩统计表:
原始 成绩/分 95 100 105 110 115 120 125 130 135 140 145 150
人数 1 2 2 5 8 10 7 16 20 15 9 5
①直接写出这100名员工原始成绩的中位数;
②若①中的中位数换算成报告成绩为90分,直接写出该公司此次测试的合格率.
24.(10分)如图,在△ABC中,D是BC的中点,F、E分别是AD及其延长线上的点,CF∥BE,连结BF、CE.
(1)求证:四边形BECF是平行四边形.
(2)①若AB=5,则AC 的长为 时,四边形BECF是菱形;
②若 AB=5,BC=6,且四边形BECF是正方形,求AF的长.
25.(10分)为了燃气使用安全,某燃气公司要求所有用户必须安装燃气报警器,当空气中的燃气浓度达到一定量时,报警系统就会报警并切断燃气阀门以保证安全,检测人员用标准天然气气瓶检测燃气报警器的有效性时,每分钟记录一次空气中的燃气浓度,下表记录了连续5 min内6个时间点的燃气浓度.
时间/min 0 1 2 3 4 5
燃气浓度/% 0 3 6 9 12 15
【探索发现】
(1)建立如图所示的平面直角坐标系,横轴表示检测时间x(min),纵轴表示空气中的燃气浓度y(%),图中已经描出以表格中数据为坐标的部分点,请你将表格中剩余的点描出.
(2)观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式;如果不在同一条直线上,请说明理由.
【结论应用】
若按这种上涨规律,当浓度达到24%时,报警系统会自动发出警报,当浓度达到50%时,会自动切断燃气阀门.
(3)预测第 min时,系统会发出警报.
(4)报警后,若无人发现,再过 min系统会自动切断燃气阀门.
26.(10分)如图,在平面直角坐标系中,四边形OABC是矩形,反比例函数y=(x>0)的图象分别与AB、BC交于点D(4,1)和点E,且点D为AB的中点.
(1)求反比例函数的表达式和点E的坐标.
(2)若一次函数y=x+m与反比例函数y=(x>0)的图象相交于点M,当点M在反比例函数图象上D、E之间的部分时(点M可与点D、E重合),直接写出m的取值范围.
27.(10分)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元,今年该型号自行车每辆售价预计比去年降低200元,若该型号自行车的销售数量与去年相同,则今年的销售总额将比去年减少10%.
(1)A型自行车去年每辆售价为多少元
(2)该车行今年计划新进一批A型自行车和新款B型自行车共60辆,且B型自行车的进货数量不超过A型自行车数量的2倍,已知A型自行车和B型自行车的进货价格分别为1 500元和1 800元,计划B型自行车销售价格为2 400元,应如何进货才能使这批自行车获利最多
【详解答案】
1.C 解析:∵1 nm=10-9 m,∴28 nm=28×10-9 m=2.8×10-8 m.故选C.
2.A 3.B 4.B
5.A 解析:矩形ABCD是中心对称图形,对称中心是对角线的交点,故A符合题意;线段AB的对称中心是线段AB的中点,故B不符合题意;矩形ABCD是轴对称图形,对称轴是过一组对边中点的直线,故C不符合题意;过线段BD的中点的垂线是线段BD的对称轴,故D不符合题意.故选A.
6.B 解析:65,67,75,65,75,80,75,88,78,80中,
平均数为×(65+67+75+65+75+80+75+88+78+80)=74.8,
65,67,75,65,75,80,75,88,78,80按从小到大的顺序排列为65,65,67,75,75,75,78,80,80,88,
∴中位数为=75,众数为75,
方差为×[(65-74.8)2×2+(67-74.8)2+(75-74.8)2×3+(78-74.8)2+(80-74.8)2×2+(88-74.8)2]=49.16.故选B.
7.B 解析:直线y=kx-4(k<0)与两坐标轴的交点坐标为(0,-4),,∵直线y=kx-4(k<0)与两坐标轴所围成的三角形面积等于4,∴|-4|××=4,解得k=-2,则直线的表达式为y=-2x-4.故选B.
8.C 解析:A.“龟兔再次赛跑”的路程为500 m,原说法正确,故此选项不符合题意;B.乌龟在途中休息了35-30=5(min),兔子在途中休息了50-10=40(min),兔子比乌龟多休息了35 min,原说法正确,故此选项不符合题意;C.兔子和乌龟同时从起点出发,都走了500 m,原说法错误,故此选项符合题意;D.比赛结果,兔子比乌龟早5 min到达终点,原说法正确,故此选项不符合题意.故选C.
9.A 解析:由题意可知B(0,-1),
∵直线y=x-1与y1=交于点C,
∴S△OCE=k.
设D,
∴S△BOD=×1×(-x)=-x.
∵△COE的面积与△BOD的面积相等,
∴k=-x.∴k=-x.
∴D(-k,-2).
∵D点在直线y=x-1上,
∴-2=-k-1.∴k=2.故选A.
10.D 解析:当a=2,即点Q的运动速度与点P的运动速度都是2 cm/s时,若△BPE≌△CQP,则BP=CQ,BE=CP.∵AB=BC=10 cm,AE=4 cm,∴BE=CP=6 cm,∴BP=10-6=4(cm),∴运动时间=4÷2=2(s).当a≠2,即点Q的运动速度与点P的运动速度不相等时,∴BP≠CQ.∵∠B=∠C=90°,∴要使△BPE与△CQP全等,只要BP=PC=5 cm,CQ=BE=6 cm,∴点P、Q运动的时间t==2.5(s).故选D.
11.∠A=90°(答案不唯一)
12. 解析:原式=÷=·=.
13. 解析:数据的平均数=×(3-4-3+7+3+0)=1,方差s2=×[(3-1)2+(-4-1)2+(-3-1)2+(7-1)2+(3-1)2+(0-1)2]=.
14.4
16.4-8 解析:由题意可知,BC=EF=AD=4,AE=AB,
∵DE=EF=4,
∴AE=AB==,
∴S四边形ABCE=S矩形ABCD-S△ADE=AB·AD-AD·DE=×4-×4×4=4-8.
17.解:原式=·
=·
=·
=.
∵a2+2a-15=0,∴a2+2a=15,
∴原式=.
18.解:设B型机器人每小时搬运x kg化工原料,则A型机器人每小时搬运(x+30)kg化工原料,
根据题意,得=,解得x=60,
经检验,x=60是原方程的解,且符合题意,
∴x+30=60+30=90.
答:A型机器人每小时搬运90 kg化工原料,B型机器人每小时搬运60 kg化工原料.
19.证明:(1)∵四边形ABCD是平行四边形,
∴AO=CO,AB=DC.
∵BD⊥AC,
∴∠AOB=∠COB=90°.
在△AOB和△COB中,
∴△AOB≌△COB(S.A.S.).
∴AB=CB.
同理可得△DOA≌△DOC(S.A.S.),则DA=DC,
又∵AB=CD,
∴AB=BC=CD=DA.
∴ ABCD是菱形.
(2)∵四边形ABCD是平行四边形,AD=5,AC=8,BD=6.
∴DO=BO=BD=3,AO=CO=AC=4.
在△AOD中,AD2=25,AO2+OD2=42+32=25,
∴AD2=AO2+OD2.
∴△AOD是直角三角形,且∠AOD=90°.
∴AC⊥BD.
∴ ABCD是菱形.
20.解:(1)设一次函数的表达式为y=kx+b,
把x=2,y=4;x=-1,y=1分别代入得
解得
所以一次函数的表达式为y=x+2.
(2)把(-2,m)代入y=x+2得m=-2+2=0,
把点(3,n)代入y=x+2得n=3+2=5,
所以m
证明:∵∠B=∠AED,∴BC∥DE,
∵AB∥CD,
∴四边形BCDE为平行四边形.
②
证明:∵AE=BE,AE=CD,
∴BE=CD,
∵AB∥CD,
∴四边形BCDE为平行四边形.
(答案不唯一,任选其一即可)
(2)由(1)可知,四边形BCDE为平行四边形,∴DE=BC=10,
∵AD⊥AB,∴∠A=90°,
∴AE===6,即线段AE的长为6.
22.解:(1)∵反比例函数y=(k2≠0)的图象与一次函数y=k1x+b(k1≠0)的图象相交于点A(3,4)、B(-4,m),
∴4=.∴k2=12.
∴反比例函数的表达式为y=.
∴m==-3.
∴点B的坐标为(-4,-3).
∴解得
∴一次函数的表达式为y=x+1.
(2)∵A(3,4),∴OA==5.
∵OA=OD,∴OD=5.
∴△AOD的面积=×5×4=10.
23.解:(1)当p=100时,甲的报告成绩为y==76 (分),
乙的报告成绩为
y=+80=92(分).
(2)∵92>80,∴当y=92时,+80=92,得x丙=90+p.
∵64<80,∴当y=64时,=64,得x丁=p.
∵x丙-x丁=40,∴90+p-p=40.
解得p=125.
(3)①中位数为130分.
②合格率为95%.
解法提示:①共计100名员工,且原始成绩已经从小到大排列好,
∴中位数是第50,51名员工原始成绩的平均数,
由表格得第50,51名员工原始成绩都是130分,
∴中位数为130分.
②当p>130时,则90=,
解得p=<130,故不成立,舍去;
当p≤130时,
则90=+80,
解得p=110,符合题意.
∴由表格得到原始成绩为110分及110分以上的人数为100-(1+2+2)=95,
∴合格率为×100%=95%.
24.解:(1)证明:∵D是BC的中点,
∴BD=CD,∴CF∥BE,
∴∠CFD=∠BED,
在△CFD和△BED中,
∴△CFD≌△BED(A.A.S.),
∴CF=BE,
∴四边形BECF是平行四边形.
(2)①5
②∵四边形BECF是正方形,
∴EF=BC=6,EF⊥BC,
∵D是BC的中点,
∴BD=CD=DF=DE=3,
∴AD===4,
∴AF=AD-DF=4-3=1.
25.解:(1)描点如图:
(2)观察可知它们在同一条直线上,
设直线所对应的函数表达式为y=kx+b(k≠0),
将点(0,0),(1,3)代入得
解得∴这条直线所对应的函数表达式为y=3x.
(3)8
(4)
26.解:(1)把(4,1)代人y=,得1=,解得k=4,
∴反比例函数的表达式为y=.
∵点A在x轴上,点D的纵坐标为1,D为AB的中点,
∴点B的纵坐标为2.
又∵四边形OABC为矩形,∴BE∥x轴,∴点E的纵坐标为2.
设点E的横坐标为a,则2=,解得a=2,
∴点E的坐标为(2,2).
(2)-3≤m≤0.
解法提示:当点M与点D重合时,
把(4,1)代入y=x+m,得1=4+m,解得m=-3.
当点M与点E重合时,
把(2,2)代入y=x+m,得2=2+m,解得m=0.
∴m的取值范围为-3≤m≤0.
27.解:(1)设A型自行车去年每辆售价为x元,则今年每辆售价为(x-200)元,
由题意,得=,
解得x=2 000.经检验,x=2 000是原方程的解,且符合题意.
答:A型自行车去年每辆售价为2 000元.
(2)设今年新进A型自行车a辆,则新进B型自行车(60-a)辆,获利y元.
由题意,得y=(1 800-1 500)a+(2 400-1 800)(60-a)=-300a+36 000.
∵B型自行车的进货数量不超过A型自行车数量的2倍,
∴60-a≤2a.∴a≥20.
∵y=-300a+36 000,-300<0,
∴y随a的增大而减少,∴当a=20时,y最大.
此时B型自行车进货数量为60-20=40(辆).
答:当新进A型自行车20辆,B型自行车 40辆时,才能使这批自行车获利最多.
同课章节目录
