第二学期期中评估测试卷(含答案)2024-2025学年数学华东师大版八年级下册
文档属性
| 名称 | 第二学期期中评估测试卷(含答案)2024-2025学年数学华东师大版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 174.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 14:11:25 | ||
图片预览



文档简介
第二学期期中评估测试卷
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.(2024烟台中考)目前全球最薄的手撕钢产自中国,厚度只有0.015 mm,约是A4纸厚度的六分之一.已知1 mm=1百万纳米,0.015 mm等于多少纳米 将结果用科学记数法表示为 ( )
A.0.15×103 nm B.1.5×104 nm
C.15×10-5 nm D.1.5×10-6 nm
2.(2024安徽中考)已知反比例函数y=(k≠0)与一次函数y=2-x的图象的一个交点的横坐标为3,则k的值为 ( )
A.-3 B.-1 C.1 D.3
3.(2024德阳中考)正比例函数y=kx(k≠0)的图象如图所示,则k的值可能是 ( )
A. B.- C.-1 D.-
4.下列关于分式方程+1=的解的情况判断正确的是 ( )
A.x=1.5 B.x=-0.5 C.x=0.5 D.无解
5.化简分式1-·(x2-1)的结果为 ( )
A.2+3x B.3x C.2-3x D.-3x
6.一次函数y=(3a-7)x+a-2的图象与y轴的交点在x轴的上方,且y随着x的增大而减小,则a的取值范围是 ( )
A.a>2 B.a> C.27.(2024广元中考)我市把提升城市园林绿化水平作为推进城市更新行动的有效抓手,从2023年开始通过拆违建绿、见缝插绿等方式在全域打造多个小而美的“口袋公园”,现需要购买A、B两种绿植,已知A种绿植单价是B种绿植单价的3倍,用6 750元购买的A种绿植比用3 000元购买的B种绿植少50株.设B种绿植单价是x元,则可列方程是 ( )
A.-50= B.-50= C.+50= D.+50=
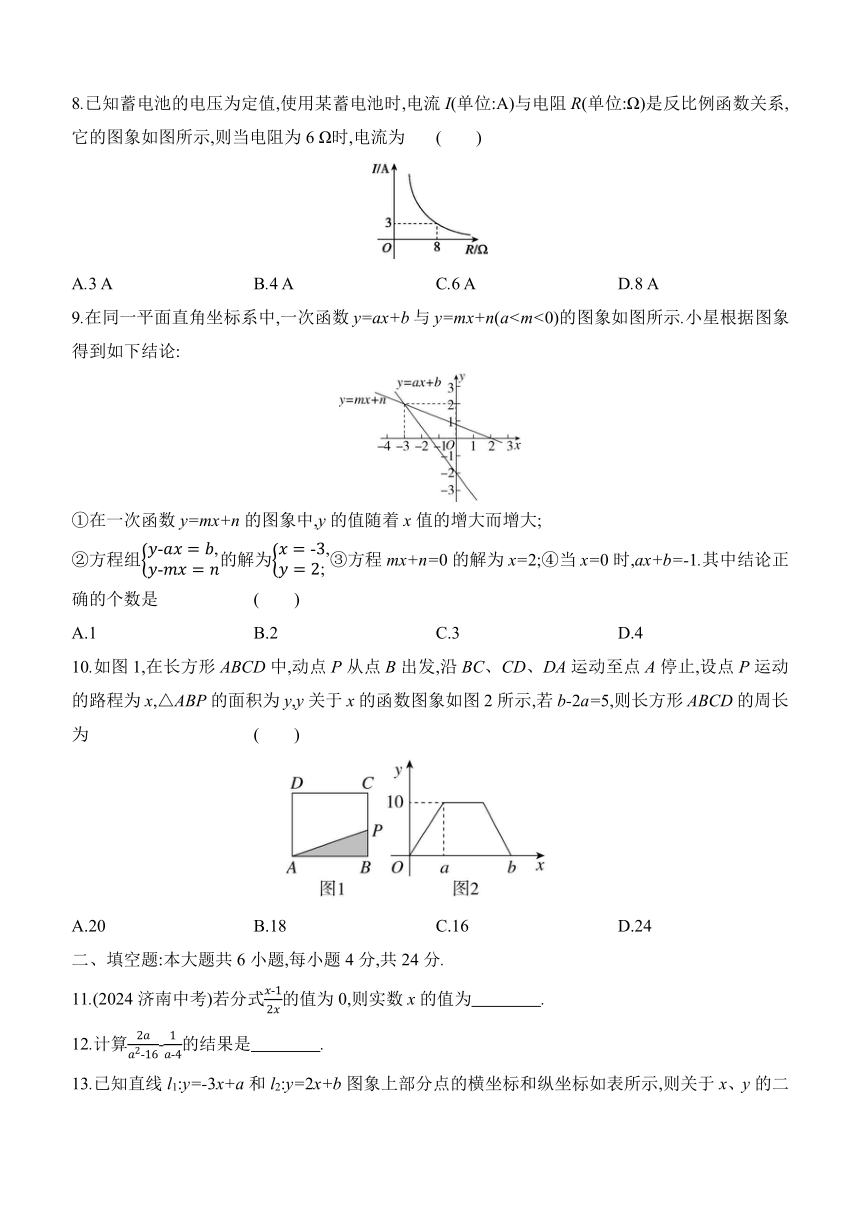
8.已知蓄电池的电压为定值,使用某蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,则当电阻为6 Ω时,电流为 ( )
A.3 A B.4 A C.6 A D.8 A
9.在同一平面直角坐标系中,一次函数y=ax+b与y=mx+n(a①在一次函数y=mx+n的图象中,y的值随着x值的增大而增大;
②方程组的解为③方程mx+n=0的解为x=2;④当x=0时,ax+b=-1.其中结论正确的个数是 ( )
A.1 B.2 C.3 D.4
10.如图1,在长方形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,y关于x的函数图象如图2所示,若b-2a=5,则长方形ABCD的周长为 ( )
A.20 B.18 C.16 D.24
二、填空题:本大题共6小题,每小题4分,共24分.
11.(2024济南中考)若分式的值为0,则实数x的值为 .
12.计算-的结果是 .
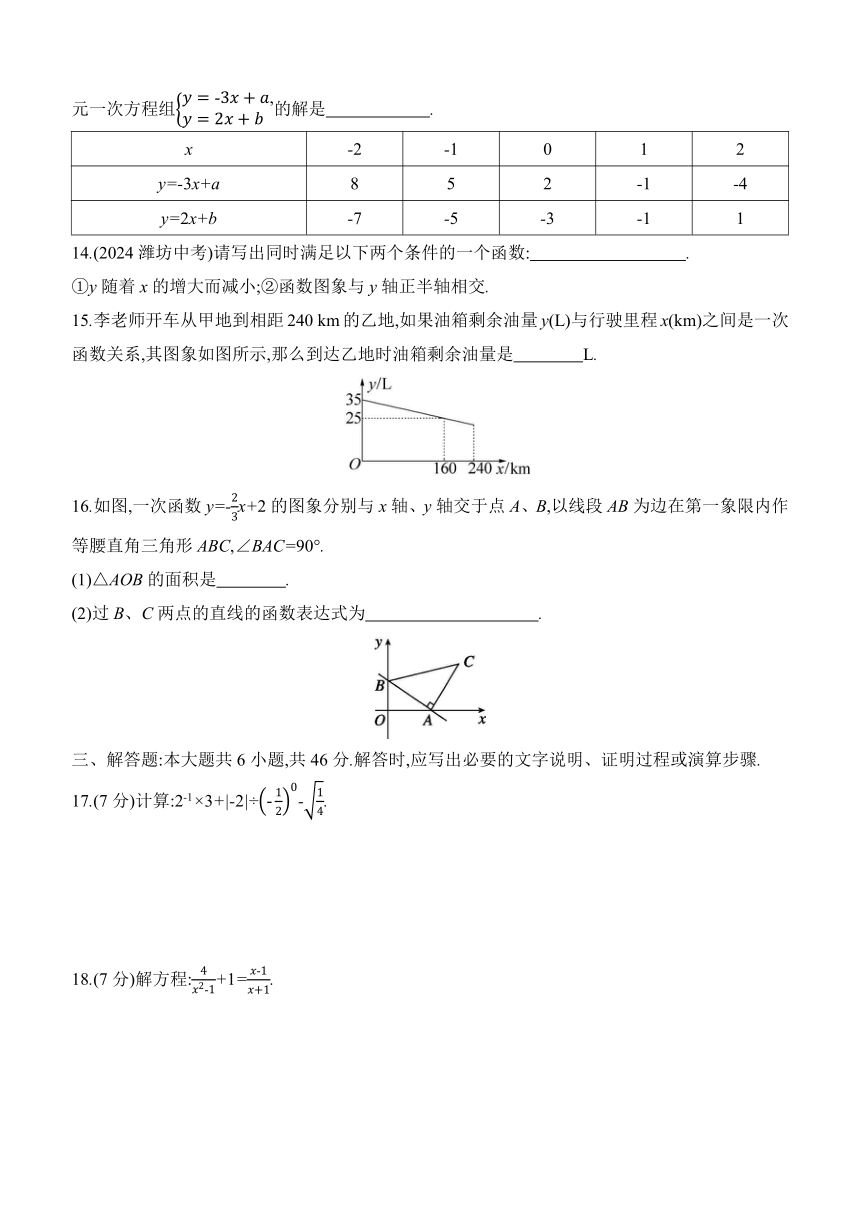
13.已知直线l1:y=-3x+a和l2:y=2x+b图象上部分点的横坐标和纵坐标如表所示,则关于x、y的二元一次方程组的解是 .
x -2 -1 0 1 2
y=-3x+a 8 5 2 -1 -4
y=2x+b -7 -5 -3 -1 1
14.(2024潍坊中考)请写出同时满足以下两个条件的一个函数: .
①y随着x的增大而减小;②函数图象与y轴正半轴相交.
15.李老师开车从甲地到相距240 km的乙地,如果油箱剩余油量y(L)与行驶里程x(km)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是 L.
16.如图,一次函数y=-x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰直角三角形ABC,∠BAC=90°.
(1)△AOB的面积是 .
(2)过B、C两点的直线的函数表达式为 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(7分)计算:2-1×3+|-2|÷-.
18.(7分)解方程:+1=.
19.(8分)先化简:÷,然后再从-220.(8分)某生物小组观察一植物生长,得到植物高度y(cm)与观察时间x(天)的关系,并画出如图所示的图象(AC是线段,直线CD∥x轴).
(1)该植物从观察时起,多少天以后停止长高
(2)求直线AC的表达式,并求该植物最多长了多少厘米
21.(8分)某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球.回校后,王老师和李老师编写了一道题:
同学们,请求出篮球和排球的单价各是多少元
22.(8分)已知一次函数y=kx+b(k、b为常数,且k≠0)的图象经过A(2,7)、B(0,3).
(1)求该一次函数的表达式,并画出它的图象.
(2)判断点P(-1,2)是否在该一次函数的图象上.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,点A(2,6)、B(4,n)是反比例函数y=(k>0)图象上两点,AC⊥y轴于点C,BD⊥x轴于点D.
(1)求反比例函数的表达式.
(2)求五边形ABDOC 的面积.
24.(8分)(2024广元中考)近年来,中国传统服饰备受大家的青睐,走上国际时装周舞台,大放异彩.某服装店直接从工厂购进长、短两款传统服饰进行销售,进货价和销售价如表:
价格 类别
短款 长款
进货价/(元/件) 80 90
销售价/(元/件) 100 120
(1)该服装店第一次用4 300元购进长、短两款服装共50件,求两款服装分别购进的件数.
(2)第一次购进的两款服装售完后,该服装店计划再次购进长、短两款服装共200件(进货价和销售价都不变),且第二次进货总价不高于16 800元.服装店这次应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少
25.(10分)重阳节期间,某社区社居委组织本社区100位60岁以上的老年人前往某景区开展休闲旅游活动,由甲、乙两家旅店承担住宿任务.由于接待能力受限,两家旅店每家最多能接待60人住宿.甲旅店的费用是每人100元,乙旅店的费用是每人120元,如果设甲旅店安排住宿x人,乙旅店安排住宿y人,所需总费用为w元,则:
(1)如何安排两家旅店的接待人数,可使住宿费用最低
(2)经协商,两家旅店均同意实行优惠政策,其优惠幅度如下表:
人数 甲旅店 乙旅店
少于50人 一律8折优惠 7折优惠
不少于50人 5折优惠
如何安排可使住宿费用最低
26.(10分)如图,反比例函数y=(k≠0)的图象与一次函数y=mx+n(m≠0)的图象相交于A(a,-1)、B(-1,3)两点.
(1)求反比例函数和一次函数的表达式.
(2)设直线AB交y轴于点C,点N(t,0)是x轴正半轴上的一个动点,过点N作NM⊥x轴交反比例函数y=的图象于点M,连结CN、OM.若S四边形COMN>3,求t的取值范围.
27.(14分)如图1,在长方形ABCD中,AB=10 cm,BC=8 cm,点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1 cm,点Q的速度为每秒2 cm,出发a s后,点P、点Q同时改变速度,点P的速度变为每秒b cm,点Q的速度变为每秒d cm.图2是点P出发x s后△APD的面积S1(cm2)与x(s)之间的函数关系图象;图3是点Q出发x s后△AQD的面积S2(cm2)与x(s)之间的函数关系图象.
(1)参照图2,求a、b、c的值.
(2)求d的值.
(3)设点P离开点A的路程为y1(cm),点Q到点A还需走的路程为y2(cm),请分别写出动点P、Q改变速度后y1、y2与出发后的运动时间x(s)之间的函数关系式,并求出P、Q相遇时x的值.
(4)当点Q出发 s时,点P、点Q在运动路线上相距的路程为25 cm.
【详解答案】
1.B 解析:由题意可得1 mm=1百万纳米=106 nm,
则0.015 mm=1.5×10-2×106 nm=1.5×104 nm.
故选B.
2.A 解析:将x=3代入y=2-x中,得y=-1,将(3,-1)代入y=中,得k=-3.故选A.
3.A 解析:由题图知,函数值y随x的增大而增大,
∴k>0,∴k的值可能是.故选A.
4.D 解析:去分母,得2(x-2)+2(2x-1)=-3,解得x=,经检验,x=不是原方程的解,故原方程无解.故选D.
5.D 解析:原式=1-·(x+1)(x-1)=1-[2(x+1)+x-1]=1-(2x+2+x-1)=1-2x-2-x+1=-3x.
故选D.
6.C 解析:∵关于x的一次函数y=(3a-7)x+a-2的图象与y轴的交点在x轴的上方,且y随着x的增大而减小,
∴解得27.C 解析:∵A种绿植单价是B种绿植单价的3倍,B种绿植单价是x元,
∴A种绿植单价是3x元.
根据题意得+50=.
故选C.
8.B 解析:设该反比例函数的表达式为I=(k≠0),由题意可知,当R=8时,I=3,∴3=,解得k=24.∴该反比例函数的表达式为I=.∴当R=6时,I==4,即电流为4 A.故选B.
9.B 解析:①由函数图象可知,直线y=mx+n从左至右呈下降趋势,则y的值随着x值的增大而减小,故①错误;②由函数图象可知,一次函数y=ax+b与y=mx+n(a10.B 解析:根据题图2的点(a,10),可知BC=a,AB×BC=10,∴AB=,
∴BC+CD+DA=2a+=b,
∴b-2a=.
∵b-2a=5,
∴=5,∴a=4,
∴AB=5,BC=4.
∴长方形ABCD的周长为2×(5+4)=18.故选B.
11.1 解析:∵分式的值为0,
∴x-1=0且2x≠0,
解得x=1.
12. 解析:原式=-=.
13. 解析:根据表格可知,(1,-1)是直线l1:y=-3x+a和l2:y=2x+b的交点坐标,
∴的解为
14.y=-x+2(答案不唯一)
解析:∵y随着x的增大而减小,
∴一次函数的系数k<0,
又∵函数图象与y轴正半轴相交,
∴b>0,
∴同时满足以上两个条件的一次函数可以是y=-x+2.(答案不唯一)
15.20 解析:设y与x之间的函数关系式为y=kx+b(k≠0),将(0,35)、(160,25)代入,得
解得
∴y=-x+35.当x=240时,y=-×240+35=20.
16.(1)3 (2)y=x+2
解析:(1)在一次函数y=-x+2中,
令x=0,得y=2;令y=0,得x=3,
∴B的坐标是(0,2),A的坐标是(3,0).
∴S△AOB=OA·OB=3.
(2)如图,作CD⊥x轴于点D,
∵∠BAC=90°,
∴∠BAO+∠CAD=90°.
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO.
在△ABO和△CAD中,
∴△ABO≌△CAD(A.A.S.).
∴OB=AD=2,OA=CD=3,OD=OA+AD=5.则点C的坐标是(5,3).
设直线BC的函数表达式是y=kx+b(k≠0),
根据题意,得解得
∴直线BC的函数表达式是y=x+2.
17.解:原式=×3+2÷1-=3.
18.解:方程两边同乘以(x+1)(x-1),得4+x2-1=x2-2x+1,即2x=-2,解得x=-1.
检验:当x=-1时,(x+1)(x-1)=0,∴x=-1是原方程的增根,所以原方程无解.
19.解:原式=÷
=÷
=·
=,
∵x≠0且x≠±1,∴x=2,
则原式==4.
20.解:(1)根据题中图象可知,该植物从观察时起,50天以后停止长高.
(2)设直线AC的表达式是y=kx+b(k≠0),把A(0,6)、B(30,12)代入,得
解得
∴直线AC的表达式是y=x+6.
∵>0,∴y随x的增大而增大.又∵0≤x≤50,
∴当x=50时,y最大=×50+6=16,16-6=10(cm).
∴该植物最多长了10 cm.
21.解:设排球的单价为x元,则篮球的单价为(x+30)元,
根据题意,得=,解得x=50.
经检验,x=50是原方程的解.
当x=50时,x+30=80.
答:排球的单价为50元,篮球的单价为80元.
22.解:(1)把A(2,7)、B(0,3)代入y=kx+b,得
解得
∴该一次函数的表达式为y=2x+3.
图象如图所示:
(2)当x=-1时,y=-2+3=1,
∴点P(-1,2)不在该一次函数的图象上.
23.解:(1)∵点A(2,6)在反比例函数y=(k>0)的图象上,∴k=2×6=12.
∴反比例函数的表达式为y=.
(2)∵B(4,n)在反比例函数y=的图象上,∴n==3,∴B(4,3).
延长CA、DB交于点E,如图.
∵AC⊥y轴于点C,BD⊥x轴于点D,
∴∠ECO=∠EDO=90°,∴E(4,6),
∴AE=2,BE=3,
∴S四边形CODE=CE·DE=4×6=24,
S△ABE=AE·BE=×2×3=3.
∴S五边形ABDOC=S四边形CODE-S△ABE=24-3=21.
24.解:(1)设购进短款服装x件,购进长款服装y件,
则解得
答:长款服装购进30件,短款服装购进20件.
(2)设第二次购进m件短款服装,则购进(200-m) 件长款服装,
则80m+90(200-m)≤16 800.
∴m≥120.
设销售利润为w元,则w=(100-80)m+(120-90)(200-m)=-10m+6 000.
∵-10<0,∴w随m的增大而减小.
∴当m=120时,销售利润w最大,最大值为-10×120+6 000=4 800(元).
答:当购进120件短款服装,80件长款服装时获得最大销售利润,最大销售利润是4 800元.
25.解:(1)由题意可知,x+y=100,
w=100x+120y=100x+120(100-x)=-20x+12 000.
∵k=-20<0,
∴w随x的增大而减小.
∵甲旅店最多只能接待60人,即x≤60,
∴当x=60时,w最小,为-20×60+12 000=10 800(元).
∴甲旅店安排60人,乙旅店安排40人,可使住宿费用最低,最低为10 800元.
(2)①当y<50时,由x+y=100,y=100-x<50,得x>50,
w=100×0.8x+120×0.7y=-4x+8 400.
∵k=-4<0,∴当x越大时,w越小,
∴当x=60时,w最小,为-240+8 400=8 160(元).
②当50≤y≤60时,由x+y=100,50≤100-x≤60,
得40≤x≤50,w=100×0.8x+120×0.5y=20x+6 000.
∵k=20>0,∴当x越小时,w越小,
∴当x=40时,w最小,为20×40+6 000=6 800(元).
∵8 160>6 800,∴甲旅店安排40人,乙旅店安排60人,可使住宿费用最低,最低为6 800元.
26.解:(1)∵反比例函数y=的图象与一次函数y=mx+n的图象相交于A(a,-1)、B(-1,3)两点,
∴k=-1×3=a×(-1).
∴k=-3,a=3.
∴点A(3,-1),反比例函数的表达式为y=-.
将A(3,-1)、B(-1,3)代入y=mx+n,得
解得
∴一次函数的表达式为y=-x+2.
(2)∵直线AB交y轴于点C,
∴点C(0,2).
∴S四边形COMN=S△OMN+S△OCN=+×2t.
∵S四边形COMN>3,∴+×2t>3,∴t>.
27.解:(1)观察题图2得,x=a时,S△APD=PA·AD=×1×a×8=24,
∴a=6,
b==2,
c=8+=17.
(2)依题意得(22-6)d=28-12,
解得d=1.
(3)∵a=6,b=2,d=1,∴动点P、Q改变速度后y1、y2与出发后的运动时间x(s)之间的函数关系式为
y1=6+2(x-6)=2x-6,
y2=28-[12+1×(x-6)]=22-x,
P、Q相遇时,依题意得2x-6=22-x,
∴x=.
(4)1或19
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.(2024烟台中考)目前全球最薄的手撕钢产自中国,厚度只有0.015 mm,约是A4纸厚度的六分之一.已知1 mm=1百万纳米,0.015 mm等于多少纳米 将结果用科学记数法表示为 ( )
A.0.15×103 nm B.1.5×104 nm
C.15×10-5 nm D.1.5×10-6 nm
2.(2024安徽中考)已知反比例函数y=(k≠0)与一次函数y=2-x的图象的一个交点的横坐标为3,则k的值为 ( )
A.-3 B.-1 C.1 D.3
3.(2024德阳中考)正比例函数y=kx(k≠0)的图象如图所示,则k的值可能是 ( )
A. B.- C.-1 D.-
4.下列关于分式方程+1=的解的情况判断正确的是 ( )
A.x=1.5 B.x=-0.5 C.x=0.5 D.无解
5.化简分式1-·(x2-1)的结果为 ( )
A.2+3x B.3x C.2-3x D.-3x
6.一次函数y=(3a-7)x+a-2的图象与y轴的交点在x轴的上方,且y随着x的增大而减小,则a的取值范围是 ( )
A.a>2 B.a> C.2
A.-50= B.-50= C.+50= D.+50=
8.已知蓄电池的电压为定值,使用某蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,则当电阻为6 Ω时,电流为 ( )
A.3 A B.4 A C.6 A D.8 A
9.在同一平面直角坐标系中,一次函数y=ax+b与y=mx+n(a
②方程组的解为③方程mx+n=0的解为x=2;④当x=0时,ax+b=-1.其中结论正确的个数是 ( )
A.1 B.2 C.3 D.4
10.如图1,在长方形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,y关于x的函数图象如图2所示,若b-2a=5,则长方形ABCD的周长为 ( )
A.20 B.18 C.16 D.24
二、填空题:本大题共6小题,每小题4分,共24分.
11.(2024济南中考)若分式的值为0,则实数x的值为 .
12.计算-的结果是 .
13.已知直线l1:y=-3x+a和l2:y=2x+b图象上部分点的横坐标和纵坐标如表所示,则关于x、y的二元一次方程组的解是 .
x -2 -1 0 1 2
y=-3x+a 8 5 2 -1 -4
y=2x+b -7 -5 -3 -1 1
14.(2024潍坊中考)请写出同时满足以下两个条件的一个函数: .
①y随着x的增大而减小;②函数图象与y轴正半轴相交.
15.李老师开车从甲地到相距240 km的乙地,如果油箱剩余油量y(L)与行驶里程x(km)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是 L.
16.如图,一次函数y=-x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰直角三角形ABC,∠BAC=90°.
(1)△AOB的面积是 .
(2)过B、C两点的直线的函数表达式为 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(7分)计算:2-1×3+|-2|÷-.
18.(7分)解方程:+1=.
19.(8分)先化简:÷,然后再从-2
(1)该植物从观察时起,多少天以后停止长高
(2)求直线AC的表达式,并求该植物最多长了多少厘米
21.(8分)某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球.回校后,王老师和李老师编写了一道题:
同学们,请求出篮球和排球的单价各是多少元
22.(8分)已知一次函数y=kx+b(k、b为常数,且k≠0)的图象经过A(2,7)、B(0,3).
(1)求该一次函数的表达式,并画出它的图象.
(2)判断点P(-1,2)是否在该一次函数的图象上.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,点A(2,6)、B(4,n)是反比例函数y=(k>0)图象上两点,AC⊥y轴于点C,BD⊥x轴于点D.
(1)求反比例函数的表达式.
(2)求五边形ABDOC 的面积.
24.(8分)(2024广元中考)近年来,中国传统服饰备受大家的青睐,走上国际时装周舞台,大放异彩.某服装店直接从工厂购进长、短两款传统服饰进行销售,进货价和销售价如表:
价格 类别
短款 长款
进货价/(元/件) 80 90
销售价/(元/件) 100 120
(1)该服装店第一次用4 300元购进长、短两款服装共50件,求两款服装分别购进的件数.
(2)第一次购进的两款服装售完后,该服装店计划再次购进长、短两款服装共200件(进货价和销售价都不变),且第二次进货总价不高于16 800元.服装店这次应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少
25.(10分)重阳节期间,某社区社居委组织本社区100位60岁以上的老年人前往某景区开展休闲旅游活动,由甲、乙两家旅店承担住宿任务.由于接待能力受限,两家旅店每家最多能接待60人住宿.甲旅店的费用是每人100元,乙旅店的费用是每人120元,如果设甲旅店安排住宿x人,乙旅店安排住宿y人,所需总费用为w元,则:
(1)如何安排两家旅店的接待人数,可使住宿费用最低
(2)经协商,两家旅店均同意实行优惠政策,其优惠幅度如下表:
人数 甲旅店 乙旅店
少于50人 一律8折优惠 7折优惠
不少于50人 5折优惠
如何安排可使住宿费用最低
26.(10分)如图,反比例函数y=(k≠0)的图象与一次函数y=mx+n(m≠0)的图象相交于A(a,-1)、B(-1,3)两点.
(1)求反比例函数和一次函数的表达式.
(2)设直线AB交y轴于点C,点N(t,0)是x轴正半轴上的一个动点,过点N作NM⊥x轴交反比例函数y=的图象于点M,连结CN、OM.若S四边形COMN>3,求t的取值范围.
27.(14分)如图1,在长方形ABCD中,AB=10 cm,BC=8 cm,点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1 cm,点Q的速度为每秒2 cm,出发a s后,点P、点Q同时改变速度,点P的速度变为每秒b cm,点Q的速度变为每秒d cm.图2是点P出发x s后△APD的面积S1(cm2)与x(s)之间的函数关系图象;图3是点Q出发x s后△AQD的面积S2(cm2)与x(s)之间的函数关系图象.
(1)参照图2,求a、b、c的值.
(2)求d的值.
(3)设点P离开点A的路程为y1(cm),点Q到点A还需走的路程为y2(cm),请分别写出动点P、Q改变速度后y1、y2与出发后的运动时间x(s)之间的函数关系式,并求出P、Q相遇时x的值.
(4)当点Q出发 s时,点P、点Q在运动路线上相距的路程为25 cm.
【详解答案】
1.B 解析:由题意可得1 mm=1百万纳米=106 nm,
则0.015 mm=1.5×10-2×106 nm=1.5×104 nm.
故选B.
2.A 解析:将x=3代入y=2-x中,得y=-1,将(3,-1)代入y=中,得k=-3.故选A.
3.A 解析:由题图知,函数值y随x的增大而增大,
∴k>0,∴k的值可能是.故选A.
4.D 解析:去分母,得2(x-2)+2(2x-1)=-3,解得x=,经检验,x=不是原方程的解,故原方程无解.故选D.
5.D 解析:原式=1-·(x+1)(x-1)=1-[2(x+1)+x-1]=1-(2x+2+x-1)=1-2x-2-x+1=-3x.
故选D.
6.C 解析:∵关于x的一次函数y=(3a-7)x+a-2的图象与y轴的交点在x轴的上方,且y随着x的增大而减小,
∴解得2
∴A种绿植单价是3x元.
根据题意得+50=.
故选C.
8.B 解析:设该反比例函数的表达式为I=(k≠0),由题意可知,当R=8时,I=3,∴3=,解得k=24.∴该反比例函数的表达式为I=.∴当R=6时,I==4,即电流为4 A.故选B.
9.B 解析:①由函数图象可知,直线y=mx+n从左至右呈下降趋势,则y的值随着x值的增大而减小,故①错误;②由函数图象可知,一次函数y=ax+b与y=mx+n(a
∴BC+CD+DA=2a+=b,
∴b-2a=.
∵b-2a=5,
∴=5,∴a=4,
∴AB=5,BC=4.
∴长方形ABCD的周长为2×(5+4)=18.故选B.
11.1 解析:∵分式的值为0,
∴x-1=0且2x≠0,
解得x=1.
12. 解析:原式=-=.
13. 解析:根据表格可知,(1,-1)是直线l1:y=-3x+a和l2:y=2x+b的交点坐标,
∴的解为
14.y=-x+2(答案不唯一)
解析:∵y随着x的增大而减小,
∴一次函数的系数k<0,
又∵函数图象与y轴正半轴相交,
∴b>0,
∴同时满足以上两个条件的一次函数可以是y=-x+2.(答案不唯一)
15.20 解析:设y与x之间的函数关系式为y=kx+b(k≠0),将(0,35)、(160,25)代入,得
解得
∴y=-x+35.当x=240时,y=-×240+35=20.
16.(1)3 (2)y=x+2
解析:(1)在一次函数y=-x+2中,
令x=0,得y=2;令y=0,得x=3,
∴B的坐标是(0,2),A的坐标是(3,0).
∴S△AOB=OA·OB=3.
(2)如图,作CD⊥x轴于点D,
∵∠BAC=90°,
∴∠BAO+∠CAD=90°.
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO.
在△ABO和△CAD中,
∴△ABO≌△CAD(A.A.S.).
∴OB=AD=2,OA=CD=3,OD=OA+AD=5.则点C的坐标是(5,3).
设直线BC的函数表达式是y=kx+b(k≠0),
根据题意,得解得
∴直线BC的函数表达式是y=x+2.
17.解:原式=×3+2÷1-=3.
18.解:方程两边同乘以(x+1)(x-1),得4+x2-1=x2-2x+1,即2x=-2,解得x=-1.
检验:当x=-1时,(x+1)(x-1)=0,∴x=-1是原方程的增根,所以原方程无解.
19.解:原式=÷
=÷
=·
=,
∵x≠0且x≠±1,∴x=2,
则原式==4.
20.解:(1)根据题中图象可知,该植物从观察时起,50天以后停止长高.
(2)设直线AC的表达式是y=kx+b(k≠0),把A(0,6)、B(30,12)代入,得
解得
∴直线AC的表达式是y=x+6.
∵>0,∴y随x的增大而增大.又∵0≤x≤50,
∴当x=50时,y最大=×50+6=16,16-6=10(cm).
∴该植物最多长了10 cm.
21.解:设排球的单价为x元,则篮球的单价为(x+30)元,
根据题意,得=,解得x=50.
经检验,x=50是原方程的解.
当x=50时,x+30=80.
答:排球的单价为50元,篮球的单价为80元.
22.解:(1)把A(2,7)、B(0,3)代入y=kx+b,得
解得
∴该一次函数的表达式为y=2x+3.
图象如图所示:
(2)当x=-1时,y=-2+3=1,
∴点P(-1,2)不在该一次函数的图象上.
23.解:(1)∵点A(2,6)在反比例函数y=(k>0)的图象上,∴k=2×6=12.
∴反比例函数的表达式为y=.
(2)∵B(4,n)在反比例函数y=的图象上,∴n==3,∴B(4,3).
延长CA、DB交于点E,如图.
∵AC⊥y轴于点C,BD⊥x轴于点D,
∴∠ECO=∠EDO=90°,∴E(4,6),
∴AE=2,BE=3,
∴S四边形CODE=CE·DE=4×6=24,
S△ABE=AE·BE=×2×3=3.
∴S五边形ABDOC=S四边形CODE-S△ABE=24-3=21.
24.解:(1)设购进短款服装x件,购进长款服装y件,
则解得
答:长款服装购进30件,短款服装购进20件.
(2)设第二次购进m件短款服装,则购进(200-m) 件长款服装,
则80m+90(200-m)≤16 800.
∴m≥120.
设销售利润为w元,则w=(100-80)m+(120-90)(200-m)=-10m+6 000.
∵-10<0,∴w随m的增大而减小.
∴当m=120时,销售利润w最大,最大值为-10×120+6 000=4 800(元).
答:当购进120件短款服装,80件长款服装时获得最大销售利润,最大销售利润是4 800元.
25.解:(1)由题意可知,x+y=100,
w=100x+120y=100x+120(100-x)=-20x+12 000.
∵k=-20<0,
∴w随x的增大而减小.
∵甲旅店最多只能接待60人,即x≤60,
∴当x=60时,w最小,为-20×60+12 000=10 800(元).
∴甲旅店安排60人,乙旅店安排40人,可使住宿费用最低,最低为10 800元.
(2)①当y<50时,由x+y=100,y=100-x<50,得x>50,
w=100×0.8x+120×0.7y=-4x+8 400.
∵k=-4<0,∴当x越大时,w越小,
∴当x=60时,w最小,为-240+8 400=8 160(元).
②当50≤y≤60时,由x+y=100,50≤100-x≤60,
得40≤x≤50,w=100×0.8x+120×0.5y=20x+6 000.
∵k=20>0,∴当x越小时,w越小,
∴当x=40时,w最小,为20×40+6 000=6 800(元).
∵8 160>6 800,∴甲旅店安排40人,乙旅店安排60人,可使住宿费用最低,最低为6 800元.
26.解:(1)∵反比例函数y=的图象与一次函数y=mx+n的图象相交于A(a,-1)、B(-1,3)两点,
∴k=-1×3=a×(-1).
∴k=-3,a=3.
∴点A(3,-1),反比例函数的表达式为y=-.
将A(3,-1)、B(-1,3)代入y=mx+n,得
解得
∴一次函数的表达式为y=-x+2.
(2)∵直线AB交y轴于点C,
∴点C(0,2).
∴S四边形COMN=S△OMN+S△OCN=+×2t.
∵S四边形COMN>3,∴+×2t>3,∴t>.
27.解:(1)观察题图2得,x=a时,S△APD=PA·AD=×1×a×8=24,
∴a=6,
b==2,
c=8+=17.
(2)依题意得(22-6)d=28-12,
解得d=1.
(3)∵a=6,b=2,d=1,∴动点P、Q改变速度后y1、y2与出发后的运动时间x(s)之间的函数关系式为
y1=6+2(x-6)=2x-6,
y2=28-[12+1×(x-6)]=22-x,
P、Q相遇时,依题意得2x-6=22-x,
∴x=.
(4)1或19
同课章节目录
