专题训练八 矩形中的折叠问题(含答案)2024-2025学年数学华东师大版八年级下册
文档属性
| 名称 | 专题训练八 矩形中的折叠问题(含答案)2024-2025学年数学华东师大版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 132.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 14:12:26 | ||
图片预览


文档简介
专题训练八 矩形中的折叠问题
求角度
1.如图,矩形ABCD中将△ABF沿AF翻折至△AB'F处,若AB'∥BD,∠1=26°,则∠BAF的度数为 ( )
A.57° B.58° C.59° D.60°
2.如图,点E是矩形ABCD中CD边上一点,将△BCE沿BE折叠为△BFE,点F落在边AD上,若∠AFB=50°,则∠DFE= .
3.如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60°.现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连结AH,写出与∠BEG相等的角并加以证明.
求边长
4.如图,一张矩形纸片,按照下面步骤进行折叠:
第一步,在矩形纸片的一端,利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②,把这个正方形折成两个相等的矩形,再把纸片展平.
第三步,折出内侧矩形的对角线AB,并把AB折到图③中所示的AD处.
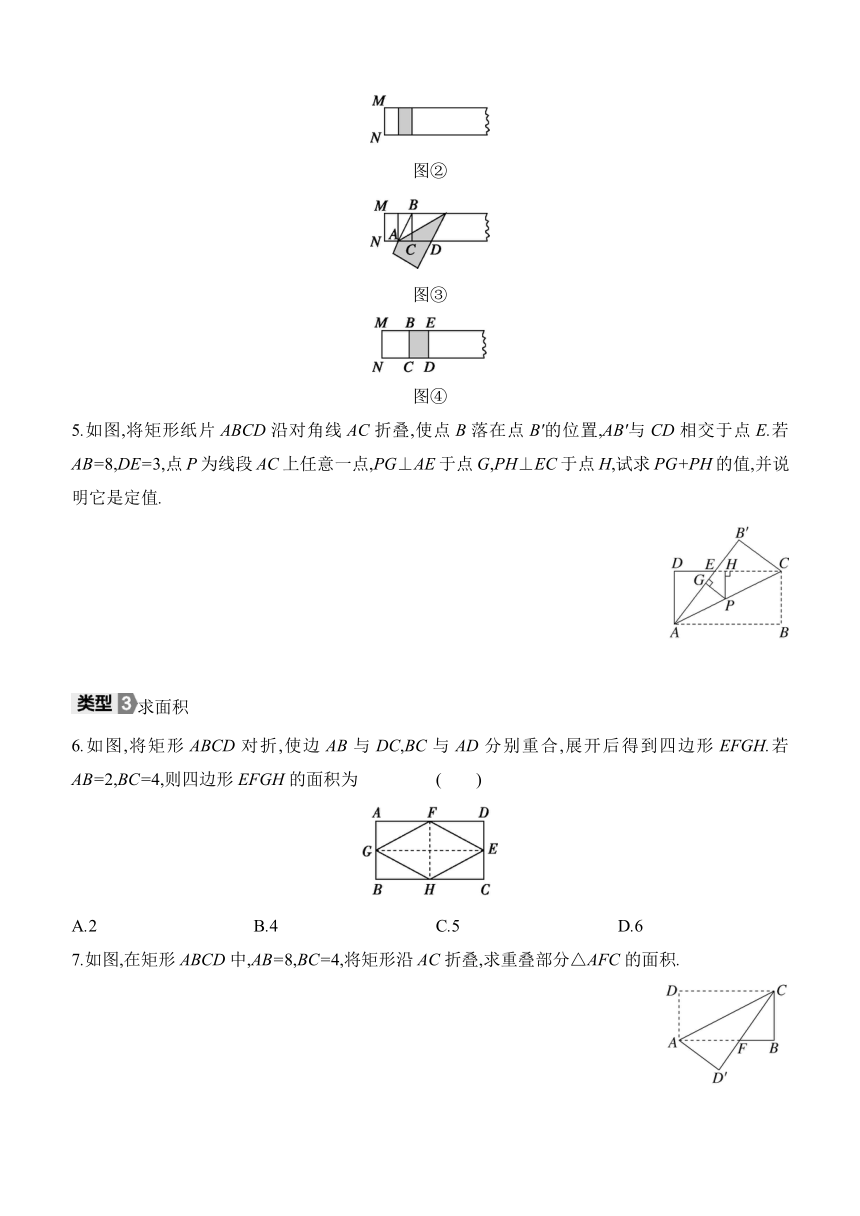
第四步,展平纸片,按照所得的点D折出DE,得出矩形BCDE(图④).则矩形BCDE的宽与长的比值为 .
图①
图②
图③
图④
5.如图,将矩形纸片ABCD沿对角线AC折叠,使点B落在点B'的位置,AB'与CD相交于点E.若AB=8,DE=3,点P为线段AC上任意一点,PG⊥AE于点G,PH⊥EC于点H,试求PG+PH的值,并说明它是定值.
求面积
6.如图,将矩形ABCD对折,使边AB与DC,BC与AD分别重合,展开后得到四边形EFGH.若AB=2,BC=4,则四边形EFGH的面积为 ( )
A.2 B.4 C.5 D.6
7.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,求重叠部分△AFC的面积.
8.如图,在矩形ABCD中,沿EF将矩形折叠,使A、C两点重合,AC与EF相交于点H.
(1)求证:△ABE≌△AGF.
(2)若AB=6,BC=8,求△ABE的面积.
求证有关结论
9.如图,已知矩形纸片ABCD,AD=2,AB=4.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.
求证:四边形AGEF是平行四边形.
10.如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE.
求证:(1)BF=DF.
(2)AE∥BD.
【详解答案】
1.B 解析:∵四边形ABCD是矩形,∴∠ABC=90°,AD∥BC.∴∠AFB=∠DAF.由翻折得∠B'=∠ABF=90°,∠AFB'=∠AFB,∴∠AFB'=∠DAF.∵AB'∥BD,∴∠B'AM=∠1=26°.∴∠AMB'=90°-∠B'AM=64°.∴∠AFB'+∠DAF=2∠DAF=∠AMB'=64°.∴∠DAF=32°.∴∠BAF=∠B'AF=∠B'AM+∠DAF=26°+32°=58°.故选B.
2.40° 解析:∵四边形ABCD是矩形,∴∠C=90°.由翻折可知∠EFB=∠C=90°,∴∠AFB+∠DFE=90°.∵∠AFB=50°,∴∠DFE=40°.
3.解:∠HEG=∠EHA=∠EAH=∠BEG.
证明:连结BH(图略).依据折叠的性质可得∠BEG=∠HEG,BE=EH,EG垂直平分BH.
∵点E是AB的中点,
∴AE=BE=EH.
∴∠EAH=∠EHA,∠EBH=∠EHB.
∵∠BAH+∠ABH+∠AHB=180°,
∴∠EHA+∠EHB=90°.
又∵∠HEG+∠EHB=90°,∴∠HEG=∠EHA.
∴∠BEG=∠HEG=∠EHA=∠EAH.
4. 解析:设BC=NC=MN=2,∵把这个正方形折成两个相等的矩形,∴NA=AC=1.∴AB==.∵把AB折到图③中所示的AD处,∴AD=AB=.∴CD=-1.∴矩形BCDE的宽与长的比值为.
5.解:如图,延长HP交AB于点M,则PM⊥AB.
∵∠1=∠2,PG⊥AB',
∴PM=PG.
∵CD∥AB,∴∠2=∠3.
∴∠1=∠3.
∴AE=CE=8-3=5.
在Rt△ADE中,DE=3,
∴AD==4.
∵PH+PM=AD,
∴PG+PH=AD=4.
∵AD边的长是固定不变的,
∴PG+PH是定值.
6.B 解析:∵将矩形ABCD对折,使边AB与DC,BC与AD分别重合,展开后得到四边形EFGH,∴FH⊥GE.∵FH=AB=2,GE=BC=4,∴四边形EFGH的面积为FH·GE=×2×4=4.故选B.
7.解:由折叠性质如:
∠D'CA=∠DCA,
∵四边形ABCD是矩形,
∴DC∥AB.
∴∠DCA=∠BAC.
∴∠D'CA=∠BAC.
∴AF=CF.
设BF=x,则AF=CF=8-x,
在Rt△BFC中,由勾股定理得CF2=BF2+BC2,
即(8-x)2=x2+42,解得x=3.
∴S△AFC=×8×4-×3×4=10.
8.解:(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠BAD=∠BCD.
由折叠的性质得AG=CD,
∠EAG=∠BCD,
∴AB=AG,∠BAD=∠EAG.∴∠BAE=∠GAF.
又∵AB∥CD,AE∥GF,AD∥BC,
∴∠BEA=∠EAF=∠GFA.
在△ABE和△AGF中,
∴△ABE≌△AGF(A.A.S.).
(2)设BE=x,则AE=CE=8-x.
在Rt△ABE中,AB2+BE2=AE2,
即62+x2=(8-x)2,解得x=.
∴S△ABE=AB·BE=×6×=.
9.证明:连结AF(图略),由折叠的性质可得AG=EG,∠AGF=∠EGF.
∵四边形ABCD是矩形,
∴DC∥AB.
∴∠EFG=∠AGF.
∴∠EFG=∠EGF.∴EF=EG.
又∵AG=EG,∴EF=AG.
∵DC∥AB,
∴四边形AGEF是平行四边形.
10.证明:(1)∵△BED是由△BCD沿对角线BD折叠得到的,
∴∠CBD=∠EBD.
在矩形ABCD中,AD∥BC,
∴∠CBD=∠ADB,
∴∠ADB=∠EBD,∴BF=DF.
(2)由折叠可知,BC=BE,
在矩形ABCD中,AD=BC,
∴AD=BE.
由(1)知BF=DF,
∴AD-DF=BE-BF,即AF=EF,
∴∠EAF=∠AEF.
∵∠AFE=∠DFB,
∴∠AEB=∠DBE,
∴AE∥BD.
求角度
1.如图,矩形ABCD中将△ABF沿AF翻折至△AB'F处,若AB'∥BD,∠1=26°,则∠BAF的度数为 ( )
A.57° B.58° C.59° D.60°
2.如图,点E是矩形ABCD中CD边上一点,将△BCE沿BE折叠为△BFE,点F落在边AD上,若∠AFB=50°,则∠DFE= .
3.如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60°.现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连结AH,写出与∠BEG相等的角并加以证明.
求边长
4.如图,一张矩形纸片,按照下面步骤进行折叠:
第一步,在矩形纸片的一端,利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②,把这个正方形折成两个相等的矩形,再把纸片展平.
第三步,折出内侧矩形的对角线AB,并把AB折到图③中所示的AD处.
第四步,展平纸片,按照所得的点D折出DE,得出矩形BCDE(图④).则矩形BCDE的宽与长的比值为 .
图①
图②
图③
图④
5.如图,将矩形纸片ABCD沿对角线AC折叠,使点B落在点B'的位置,AB'与CD相交于点E.若AB=8,DE=3,点P为线段AC上任意一点,PG⊥AE于点G,PH⊥EC于点H,试求PG+PH的值,并说明它是定值.
求面积
6.如图,将矩形ABCD对折,使边AB与DC,BC与AD分别重合,展开后得到四边形EFGH.若AB=2,BC=4,则四边形EFGH的面积为 ( )
A.2 B.4 C.5 D.6
7.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,求重叠部分△AFC的面积.
8.如图,在矩形ABCD中,沿EF将矩形折叠,使A、C两点重合,AC与EF相交于点H.
(1)求证:△ABE≌△AGF.
(2)若AB=6,BC=8,求△ABE的面积.
求证有关结论
9.如图,已知矩形纸片ABCD,AD=2,AB=4.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.
求证:四边形AGEF是平行四边形.
10.如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE.
求证:(1)BF=DF.
(2)AE∥BD.
【详解答案】
1.B 解析:∵四边形ABCD是矩形,∴∠ABC=90°,AD∥BC.∴∠AFB=∠DAF.由翻折得∠B'=∠ABF=90°,∠AFB'=∠AFB,∴∠AFB'=∠DAF.∵AB'∥BD,∴∠B'AM=∠1=26°.∴∠AMB'=90°-∠B'AM=64°.∴∠AFB'+∠DAF=2∠DAF=∠AMB'=64°.∴∠DAF=32°.∴∠BAF=∠B'AF=∠B'AM+∠DAF=26°+32°=58°.故选B.
2.40° 解析:∵四边形ABCD是矩形,∴∠C=90°.由翻折可知∠EFB=∠C=90°,∴∠AFB+∠DFE=90°.∵∠AFB=50°,∴∠DFE=40°.
3.解:∠HEG=∠EHA=∠EAH=∠BEG.
证明:连结BH(图略).依据折叠的性质可得∠BEG=∠HEG,BE=EH,EG垂直平分BH.
∵点E是AB的中点,
∴AE=BE=EH.
∴∠EAH=∠EHA,∠EBH=∠EHB.
∵∠BAH+∠ABH+∠AHB=180°,
∴∠EHA+∠EHB=90°.
又∵∠HEG+∠EHB=90°,∴∠HEG=∠EHA.
∴∠BEG=∠HEG=∠EHA=∠EAH.
4. 解析:设BC=NC=MN=2,∵把这个正方形折成两个相等的矩形,∴NA=AC=1.∴AB==.∵把AB折到图③中所示的AD处,∴AD=AB=.∴CD=-1.∴矩形BCDE的宽与长的比值为.
5.解:如图,延长HP交AB于点M,则PM⊥AB.
∵∠1=∠2,PG⊥AB',
∴PM=PG.
∵CD∥AB,∴∠2=∠3.
∴∠1=∠3.
∴AE=CE=8-3=5.
在Rt△ADE中,DE=3,
∴AD==4.
∵PH+PM=AD,
∴PG+PH=AD=4.
∵AD边的长是固定不变的,
∴PG+PH是定值.
6.B 解析:∵将矩形ABCD对折,使边AB与DC,BC与AD分别重合,展开后得到四边形EFGH,∴FH⊥GE.∵FH=AB=2,GE=BC=4,∴四边形EFGH的面积为FH·GE=×2×4=4.故选B.
7.解:由折叠性质如:
∠D'CA=∠DCA,
∵四边形ABCD是矩形,
∴DC∥AB.
∴∠DCA=∠BAC.
∴∠D'CA=∠BAC.
∴AF=CF.
设BF=x,则AF=CF=8-x,
在Rt△BFC中,由勾股定理得CF2=BF2+BC2,
即(8-x)2=x2+42,解得x=3.
∴S△AFC=×8×4-×3×4=10.
8.解:(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠BAD=∠BCD.
由折叠的性质得AG=CD,
∠EAG=∠BCD,
∴AB=AG,∠BAD=∠EAG.∴∠BAE=∠GAF.
又∵AB∥CD,AE∥GF,AD∥BC,
∴∠BEA=∠EAF=∠GFA.
在△ABE和△AGF中,
∴△ABE≌△AGF(A.A.S.).
(2)设BE=x,则AE=CE=8-x.
在Rt△ABE中,AB2+BE2=AE2,
即62+x2=(8-x)2,解得x=.
∴S△ABE=AB·BE=×6×=.
9.证明:连结AF(图略),由折叠的性质可得AG=EG,∠AGF=∠EGF.
∵四边形ABCD是矩形,
∴DC∥AB.
∴∠EFG=∠AGF.
∴∠EFG=∠EGF.∴EF=EG.
又∵AG=EG,∴EF=AG.
∵DC∥AB,
∴四边形AGEF是平行四边形.
10.证明:(1)∵△BED是由△BCD沿对角线BD折叠得到的,
∴∠CBD=∠EBD.
在矩形ABCD中,AD∥BC,
∴∠CBD=∠ADB,
∴∠ADB=∠EBD,∴BF=DF.
(2)由折叠可知,BC=BE,
在矩形ABCD中,AD=BC,
∴AD=BE.
由(1)知BF=DF,
∴AD-DF=BE-BF,即AF=EF,
∴∠EAF=∠AEF.
∵∠AFE=∠DFB,
∴∠AEB=∠DBE,
∴AE∥BD.
