第五章 圆 6 直线与圆的位置关系 第4课时 三角形的内切圆(含答案)
文档属性
| 名称 | 第五章 圆 6 直线与圆的位置关系 第4课时 三角形的内切圆(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-18 15:12:28 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第五章 圆
6 直线与圆的位置关系
第4课时 三角形的内切圆
轻松过关
1.下列结论中正确的是 ( )
A.三角形的内心一定在三角形内部
B.三角形的内心与外心不能重合
C.三角形的内心到三个顶点的距离相等
D.三角形的内心与三个顶点的连线必将三角形的面积三等分
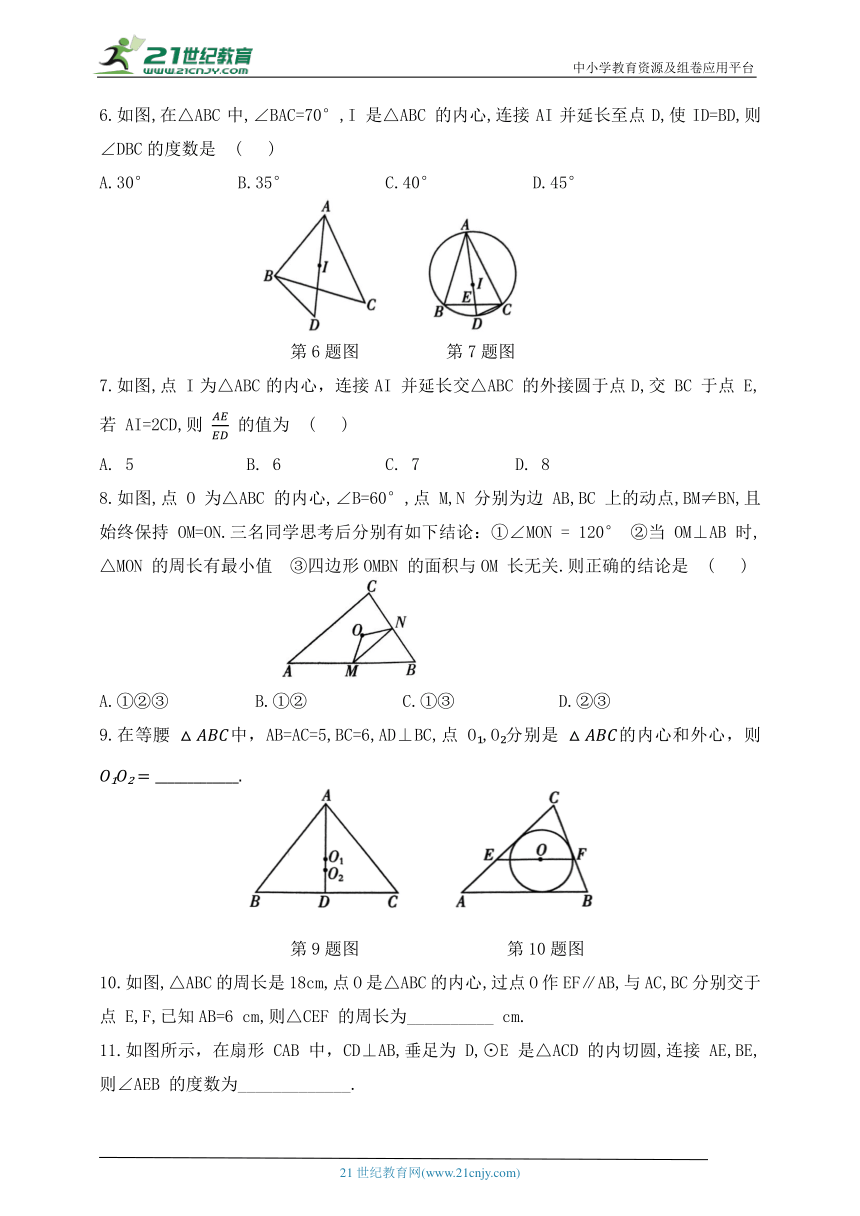
2.如图,在△ABC 中,AB=6,BC=3,CA=7,I为△ABC 的内心,连接CI并延长交AB 于点 D.记△CAI的面积为m,△DAI 的面积为n,则 ( )
第2题图 第3题图
3.如图所示,四边形 ABCD 内接于⊙O,点 I 是△ABC 的内心,∠AIC=124°,点 E 在AD 的延长线上,则∠CDE 的度数为 ( )
A. 56° B. 62° C. 68° D. 78°
4.如图所示,点I为△ABC的内心,AB=4,AC=3,BC=2,将△ACB 平移使其顶点与I 重合,则图中阴影部分的周长为 ( )
A. 4.5 B. 4 C. 3 D. 2
第4题图 第5题图
5.如图,在 Rt△ABC 中,∠ACB=90°,点O 是内心,若 CO=2,△ABC的周长为16,则△ABC的面积为 ( )
C.16 D.32
6.如图,在△ABC中,∠BAC=70°,I 是△ABC 的内心,连接AI并延长至点D,使ID=BD,则∠DBC的度数是 ( )
A.30° B.35° C.40° D.45°
第6题图 第7题图
7.如图,点 I为△ABC的内心,连接AI 并延长交△ABC 的外接圆于点D,交 BC 于点 E,若 AI=2CD,则 的值为 ( )
A. 5 B. 6 C. 7 D. 8
8.如图,点 O 为△ABC的内心,∠B=60°,点 M,N 分别为边 AB,BC上的动点,BM≠BN,且始终保持OM=ON.三名同学思考后分别有如下结论:①∠MON = 120° ②当 OM⊥AB 时,△MON 的周长有最小值 ③四边形OMBN 的面积与OM 长无关.则正确的结论是 ( )
A.①②③ B.①② C.①③ D.②③
9.在等腰 中,AB=AC=5,BC=6,AD⊥BC,点O ,O 分别是 的内心和外心,则
第9题图 第10题图
10.如图,△ABC的周长是18cm,点O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点 E,F,已知AB=6 cm,则△CEF 的周长为__________ cm.
11.如图所示,在扇形 CAB 中,CD⊥AB,垂足为 D,⊙E 是△ACD 的内切圆,连接 AE,BE,则∠AEB 的度数为_____________.
第11题图 第12题图
12.如图,在△ABC中,BC>AB,BD为△ABC的角平分线,点 G 为△ABC 的内心,过点 G作EF⊥BD交AB,BC于点E,F,AE=3,FC=6,则 EF 的长为__________.
13.已知△ABC 内接于⊙O,I 是△ABC 的内心.若∠BIC=∠BOC,则∠BAC 的度数是__________.
14.如图,在平面直角坐标系中,点A(3,0),点B(0,3),△ABC 的内心在x 轴上,求直线AC 的函数表达式.
15.如图,已知
(1)求作 的内切圆(保留作图痕迹,不要求写出作法);
(2)填空:设 的内心为O,边 BC,CA,AB上的切点依次为 D,E,F,连接 DE,DF, 若 则
16.如图,AB 是⊙O的直径,点C 是直线AB 上方的⊙O上一点.点M是 的内心.连接 AM,BM,CM,延长CM 交⊙O于点 D.
(1)若 求 BC的长;
(2)求 的度数;
(3)当点 C在直线AB 上方的⊙O 上运动时,求证:
17.如图,在 中, I为 的内心,O为 BC 上一点,过 B,I 两点的⊙O交 BC于 D点,
(1)求线段 BD 的长;
(2)求线段 BC 的长.
18.在 中,⊙O是 的内切圆,切点分别为 D,E,F.
(1)图1 中三组相等的线段分别是C若 3,BC=4,则⊙O半径长为___________;
(2)如图2,延长AC到点M,使 过点M作于点N.求证:MN是⊙O的切线.
快乐拓展
19.如图,点 E 是△ABC 的内心,AE的延长线和△ABC 的外接圆相交于点 D,与BC 相交于点 G, 则下列结论:①∠BAD=∠CAD ②若∠BAC=50°,则∠BEC=130° ③若点 G 为 BC 的中点,则∠BGD=90° ④BD=DE.其中一定正确的个数是 ( )
A.1个 B.2个 C.3个 D.4个
20.如图,点 E 是△ABC的内心,AE的延长线和△ABC 的外接圆⊙O相交于点 D,过 D作直线DG∥BC.
(1)求证:DG是⊙O的切线;
(2)求证:DE=CD;
(3)若DE=2 ,BC=8,求⊙O的半径.
参考答案
1. A 2. C 3. C 4. B 5. B 6. B 7. D 8. C
10. 12 或
14.解:设 AC交 y 轴于点 D,
∵点 A(3,0),点 B(0,3),
的内心在x轴上,∴射线 AO平分
设直线 AC的函数表达式为
则解得
∴直线 AC的函数表达式为.
15.解:(1)如图1,⊙O就是 的内切圆;
(2)如图2,连接OE,OF,DF,DE,
∵F,E分别是⊙O与AB,AC边的切点,∴∠OEA=∠OFA=90°,
在四边形 AFOE中,∠A=76°,∴∠EOF=360°-90°-90°-76°=104°,
故答案为:52°.
16.解:(1)∵AB是⊙O的直径,∴∠ACB=90°.
∵AB=10,AC=6,
∴BC的长为8;
(2)∵∠ACB=90°,∴∠CAB+∠CBA=90°.
∵点M是△ABC的内心,∴AM平分∠CAB,BM平分∠CBA.
∠CBA)=45°.
∴∠AMB=180°-(∠MAB+∠MBA)=135°.∴∠AMB=135°;
(3)证明:连接AD,BD,则∠ADB=90°,
∵点 M是△ABC的内心,∠ACB=90°,∴CM平分∠ACB.
∠MAC,
17.解:(1)如图,连接 CI 并延长,交 AB 于点E,连接ID.
∵I是△ABC的内心,∴CI平分∠ACB,BI平分
∵AC=BC,∴CE垂直平分AB,
∴IE=1,
∴△BEI∽△BID,
艮
(2)∵BI,CI分别平分∠ABC,∠ACB,
90°+∠IBC,∴∠IBC=∠BIC-90°,
∵∠CID=∠BIC-90°,∴∠IBC=∠CID,
∵∠ICB=∠ICD,∴△BIC∽△IDC,
,
解得 (负值舍去).
18.解:(1)连接OB,OD,OE,OF,如图,
∵⊙O是△ABC的内切圆,∴∠BEO=∠BDO=90°,OE=OD,
又∵BO=BO,∴Rt△BEO≌Rt△BDO(HL),∴BD=BE,同理可得AF=AD,
∵∠C=90°,⊙O是△ABC 的内切圆,∴∠C=∠OEC=∠OFC=90°,OE=OF.
∴四边形OECF 是正方形.
设OE=OF=CF=CE=x,则BE=BC-CE=4-x=BD, AF=AC-CF=3-x=AD,
∵ BD + AD = AB =5,
∴4-x+3-x=5.解得x=1,∴OE=1,即⊙O半径长为1;
故答案为:AD,BE,1;
(2)证明:过O作OH⊥MN 于点 H,连接OD,OE,OF,如图:
∵∠ANM=90°=∠ACB,∠A=∠A,AM=AB,∴△AMN≌△ABC(AAS).∴AN=AC.
∵AD=AF,∴AN-AD=AC-AF,即DN=CF.
同(1)可知,CF=OE,∴DN=OE.
∵∠ANM=90°=∠ODN=∠OHN,∴四边形OHND 是矩形.∴OH=DN.
∴OH=OE,即OH 是⊙O的半径.
∵OH⊥MN,∴MN是⊙O的切线.
19. C 解析:∵E 是△ABC的内心,∴AD 平分∠BAC.∴∠BAD=∠CAD.故①正确;
如图1,连接 BE,CE,
∵E 是△ABC的内心,
∵∠BAC=50°,∴∠ABC+∠ACB=130°.
∴∠BEC = 180°-∠EBC-∠ECB =
故②不正确;
如图2,设外心为O,连接OD,
∵∠BAD=∠CAD, ∴OD⊥BC.
∵点G为BC的中点,∴G一定在OD 上.∴∠BGD=90°.故③正确;
如图2,连接BE,∴BE平分∠ABC.∴∠ABE=∠CBE.
∵∠DBC=∠DAC=∠BAD,∴∠DBC+∠EBC=∠EBA+∠EAB.∴∠DBE=∠DEB.
∴DB=DE.故④正确,
∴一定正确的①③④,共3个.
20.解:(1)证明:连接OD 交BC 于点 H,如图,
∵点 E 是△ABC的内心,∴AD平分∠BAC,即∠BAD=∠CAD.
∴OD⊥BC,BH=CH.
∵DG∥BC,∴OD⊥DG.
∵OD 是⊙O的半径,∴DG是⊙O的切线;
(2)证明:连接BD,如图,
∵点E 是△ABC的内心,∴∠ABE=∠CBE.
∵∠DBC = ∠DAC =∠BAD,∴∠BAD+∠ABE=∠DBC+∠CBE,即∠BED=∠DBE.∴BD=DE.
∴BD=CD.∴DE=CD;
(3)连接OB,如图,由(1)得OD⊥BC,BH=CH,
∵BC=8,∴BH=CH=4.
在 Rt△BHD中, 解得 HD=2(负值舍去),
在Rt△BHO中, 即 解得r=5.
∴⊙O的半径为5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
6 直线与圆的位置关系
第4课时 三角形的内切圆
轻松过关
1.下列结论中正确的是 ( )
A.三角形的内心一定在三角形内部
B.三角形的内心与外心不能重合
C.三角形的内心到三个顶点的距离相等
D.三角形的内心与三个顶点的连线必将三角形的面积三等分
2.如图,在△ABC 中,AB=6,BC=3,CA=7,I为△ABC 的内心,连接CI并延长交AB 于点 D.记△CAI的面积为m,△DAI 的面积为n,则 ( )
第2题图 第3题图
3.如图所示,四边形 ABCD 内接于⊙O,点 I 是△ABC 的内心,∠AIC=124°,点 E 在AD 的延长线上,则∠CDE 的度数为 ( )
A. 56° B. 62° C. 68° D. 78°
4.如图所示,点I为△ABC的内心,AB=4,AC=3,BC=2,将△ACB 平移使其顶点与I 重合,则图中阴影部分的周长为 ( )
A. 4.5 B. 4 C. 3 D. 2
第4题图 第5题图
5.如图,在 Rt△ABC 中,∠ACB=90°,点O 是内心,若 CO=2,△ABC的周长为16,则△ABC的面积为 ( )
C.16 D.32
6.如图,在△ABC中,∠BAC=70°,I 是△ABC 的内心,连接AI并延长至点D,使ID=BD,则∠DBC的度数是 ( )
A.30° B.35° C.40° D.45°
第6题图 第7题图
7.如图,点 I为△ABC的内心,连接AI 并延长交△ABC 的外接圆于点D,交 BC 于点 E,若 AI=2CD,则 的值为 ( )
A. 5 B. 6 C. 7 D. 8
8.如图,点 O 为△ABC的内心,∠B=60°,点 M,N 分别为边 AB,BC上的动点,BM≠BN,且始终保持OM=ON.三名同学思考后分别有如下结论:①∠MON = 120° ②当 OM⊥AB 时,△MON 的周长有最小值 ③四边形OMBN 的面积与OM 长无关.则正确的结论是 ( )
A.①②③ B.①② C.①③ D.②③
9.在等腰 中,AB=AC=5,BC=6,AD⊥BC,点O ,O 分别是 的内心和外心,则
第9题图 第10题图
10.如图,△ABC的周长是18cm,点O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点 E,F,已知AB=6 cm,则△CEF 的周长为__________ cm.
11.如图所示,在扇形 CAB 中,CD⊥AB,垂足为 D,⊙E 是△ACD 的内切圆,连接 AE,BE,则∠AEB 的度数为_____________.
第11题图 第12题图
12.如图,在△ABC中,BC>AB,BD为△ABC的角平分线,点 G 为△ABC 的内心,过点 G作EF⊥BD交AB,BC于点E,F,AE=3,FC=6,则 EF 的长为__________.
13.已知△ABC 内接于⊙O,I 是△ABC 的内心.若∠BIC=∠BOC,则∠BAC 的度数是__________.
14.如图,在平面直角坐标系中,点A(3,0),点B(0,3),△ABC 的内心在x 轴上,求直线AC 的函数表达式.
15.如图,已知
(1)求作 的内切圆(保留作图痕迹,不要求写出作法);
(2)填空:设 的内心为O,边 BC,CA,AB上的切点依次为 D,E,F,连接 DE,DF, 若 则
16.如图,AB 是⊙O的直径,点C 是直线AB 上方的⊙O上一点.点M是 的内心.连接 AM,BM,CM,延长CM 交⊙O于点 D.
(1)若 求 BC的长;
(2)求 的度数;
(3)当点 C在直线AB 上方的⊙O 上运动时,求证:
17.如图,在 中, I为 的内心,O为 BC 上一点,过 B,I 两点的⊙O交 BC于 D点,
(1)求线段 BD 的长;
(2)求线段 BC 的长.
18.在 中,⊙O是 的内切圆,切点分别为 D,E,F.
(1)图1 中三组相等的线段分别是C若 3,BC=4,则⊙O半径长为___________;
(2)如图2,延长AC到点M,使 过点M作于点N.求证:MN是⊙O的切线.
快乐拓展
19.如图,点 E 是△ABC 的内心,AE的延长线和△ABC 的外接圆相交于点 D,与BC 相交于点 G, 则下列结论:①∠BAD=∠CAD ②若∠BAC=50°,则∠BEC=130° ③若点 G 为 BC 的中点,则∠BGD=90° ④BD=DE.其中一定正确的个数是 ( )
A.1个 B.2个 C.3个 D.4个
20.如图,点 E 是△ABC的内心,AE的延长线和△ABC 的外接圆⊙O相交于点 D,过 D作直线DG∥BC.
(1)求证:DG是⊙O的切线;
(2)求证:DE=CD;
(3)若DE=2 ,BC=8,求⊙O的半径.
参考答案
1. A 2. C 3. C 4. B 5. B 6. B 7. D 8. C
10. 12 或
14.解:设 AC交 y 轴于点 D,
∵点 A(3,0),点 B(0,3),
的内心在x轴上,∴射线 AO平分
设直线 AC的函数表达式为
则解得
∴直线 AC的函数表达式为.
15.解:(1)如图1,⊙O就是 的内切圆;
(2)如图2,连接OE,OF,DF,DE,
∵F,E分别是⊙O与AB,AC边的切点,∴∠OEA=∠OFA=90°,
在四边形 AFOE中,∠A=76°,∴∠EOF=360°-90°-90°-76°=104°,
故答案为:52°.
16.解:(1)∵AB是⊙O的直径,∴∠ACB=90°.
∵AB=10,AC=6,
∴BC的长为8;
(2)∵∠ACB=90°,∴∠CAB+∠CBA=90°.
∵点M是△ABC的内心,∴AM平分∠CAB,BM平分∠CBA.
∠CBA)=45°.
∴∠AMB=180°-(∠MAB+∠MBA)=135°.∴∠AMB=135°;
(3)证明:连接AD,BD,则∠ADB=90°,
∵点 M是△ABC的内心,∠ACB=90°,∴CM平分∠ACB.
∠MAC,
17.解:(1)如图,连接 CI 并延长,交 AB 于点E,连接ID.
∵I是△ABC的内心,∴CI平分∠ACB,BI平分
∵AC=BC,∴CE垂直平分AB,
∴IE=1,
∴△BEI∽△BID,
艮
(2)∵BI,CI分别平分∠ABC,∠ACB,
90°+∠IBC,∴∠IBC=∠BIC-90°,
∵∠CID=∠BIC-90°,∴∠IBC=∠CID,
∵∠ICB=∠ICD,∴△BIC∽△IDC,
,
解得 (负值舍去).
18.解:(1)连接OB,OD,OE,OF,如图,
∵⊙O是△ABC的内切圆,∴∠BEO=∠BDO=90°,OE=OD,
又∵BO=BO,∴Rt△BEO≌Rt△BDO(HL),∴BD=BE,同理可得AF=AD,
∵∠C=90°,⊙O是△ABC 的内切圆,∴∠C=∠OEC=∠OFC=90°,OE=OF.
∴四边形OECF 是正方形.
设OE=OF=CF=CE=x,则BE=BC-CE=4-x=BD, AF=AC-CF=3-x=AD,
∵ BD + AD = AB =5,
∴4-x+3-x=5.解得x=1,∴OE=1,即⊙O半径长为1;
故答案为:AD,BE,1;
(2)证明:过O作OH⊥MN 于点 H,连接OD,OE,OF,如图:
∵∠ANM=90°=∠ACB,∠A=∠A,AM=AB,∴△AMN≌△ABC(AAS).∴AN=AC.
∵AD=AF,∴AN-AD=AC-AF,即DN=CF.
同(1)可知,CF=OE,∴DN=OE.
∵∠ANM=90°=∠ODN=∠OHN,∴四边形OHND 是矩形.∴OH=DN.
∴OH=OE,即OH 是⊙O的半径.
∵OH⊥MN,∴MN是⊙O的切线.
19. C 解析:∵E 是△ABC的内心,∴AD 平分∠BAC.∴∠BAD=∠CAD.故①正确;
如图1,连接 BE,CE,
∵E 是△ABC的内心,
∵∠BAC=50°,∴∠ABC+∠ACB=130°.
∴∠BEC = 180°-∠EBC-∠ECB =
故②不正确;
如图2,设外心为O,连接OD,
∵∠BAD=∠CAD, ∴OD⊥BC.
∵点G为BC的中点,∴G一定在OD 上.∴∠BGD=90°.故③正确;
如图2,连接BE,∴BE平分∠ABC.∴∠ABE=∠CBE.
∵∠DBC=∠DAC=∠BAD,∴∠DBC+∠EBC=∠EBA+∠EAB.∴∠DBE=∠DEB.
∴DB=DE.故④正确,
∴一定正确的①③④,共3个.
20.解:(1)证明:连接OD 交BC 于点 H,如图,
∵点 E 是△ABC的内心,∴AD平分∠BAC,即∠BAD=∠CAD.
∴OD⊥BC,BH=CH.
∵DG∥BC,∴OD⊥DG.
∵OD 是⊙O的半径,∴DG是⊙O的切线;
(2)证明:连接BD,如图,
∵点E 是△ABC的内心,∴∠ABE=∠CBE.
∵∠DBC = ∠DAC =∠BAD,∴∠BAD+∠ABE=∠DBC+∠CBE,即∠BED=∠DBE.∴BD=DE.
∴BD=CD.∴DE=CD;
(3)连接OB,如图,由(1)得OD⊥BC,BH=CH,
∵BC=8,∴BH=CH=4.
在 Rt△BHD中, 解得 HD=2(负值舍去),
在Rt△BHO中, 即 解得r=5.
∴⊙O的半径为5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
