第五章 圆 6 直线和圆的位置关系 第2课时 切线的性质(含答案)
文档属性
| 名称 | 第五章 圆 6 直线和圆的位置关系 第2课时 切线的性质(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-18 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 圆
6 直线和圆的位置关系
第2课时 切线的性质
轻松过关
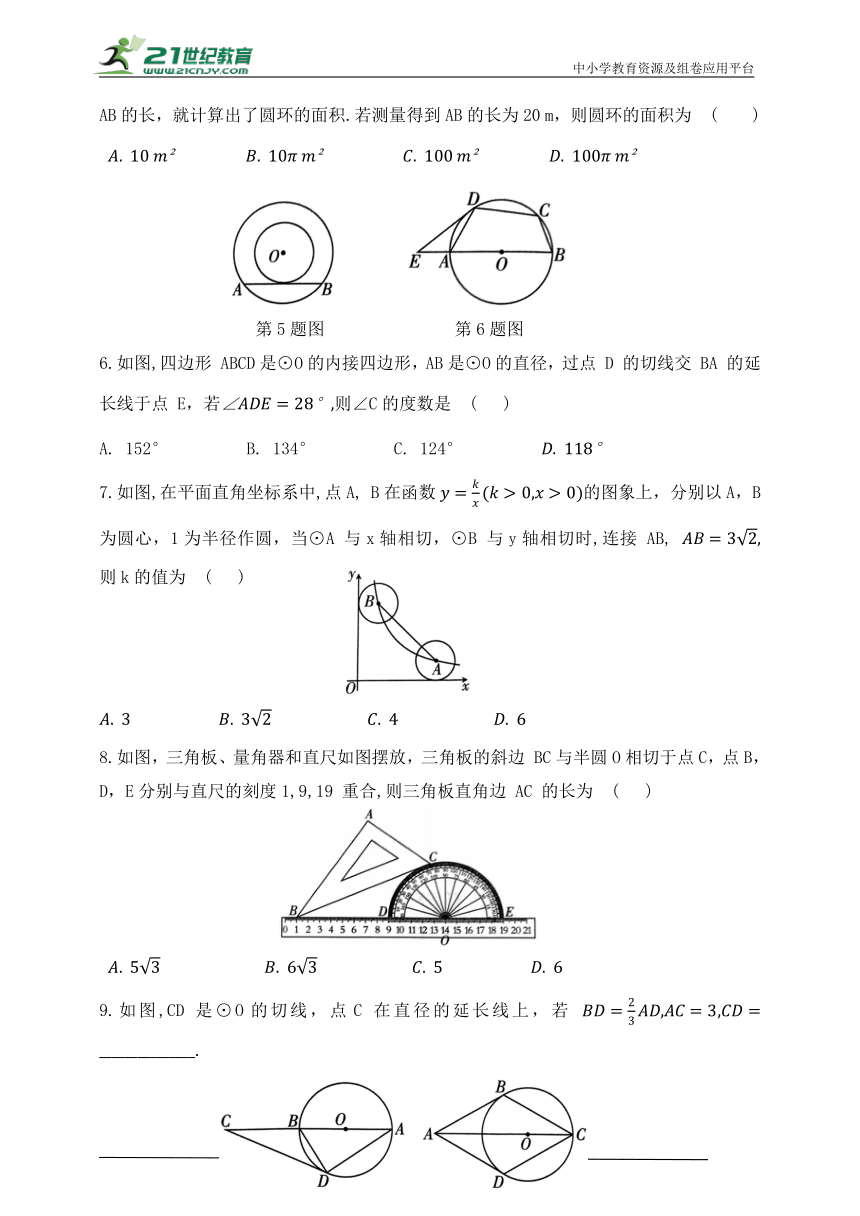
1.如图,在⊙O中,CD切⊙O于点 C,若 则 的大小为 ( )
第1题图 第2题图
2.如图,⊙O 是等边的外接圆,过点 A 作⊙O的切线交BO 的延长线于点 D,若OB=1,则 OD 的长为 ( )
A. 2 B. 3
3.当宽为3 cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为 ( )
第3题图 第4题图
4.如图,AB是圆O的直径,弦AD平分∠BAC,过点 D 的切线交 AC 于点 E,则下列结论错误的是 ( )
∥
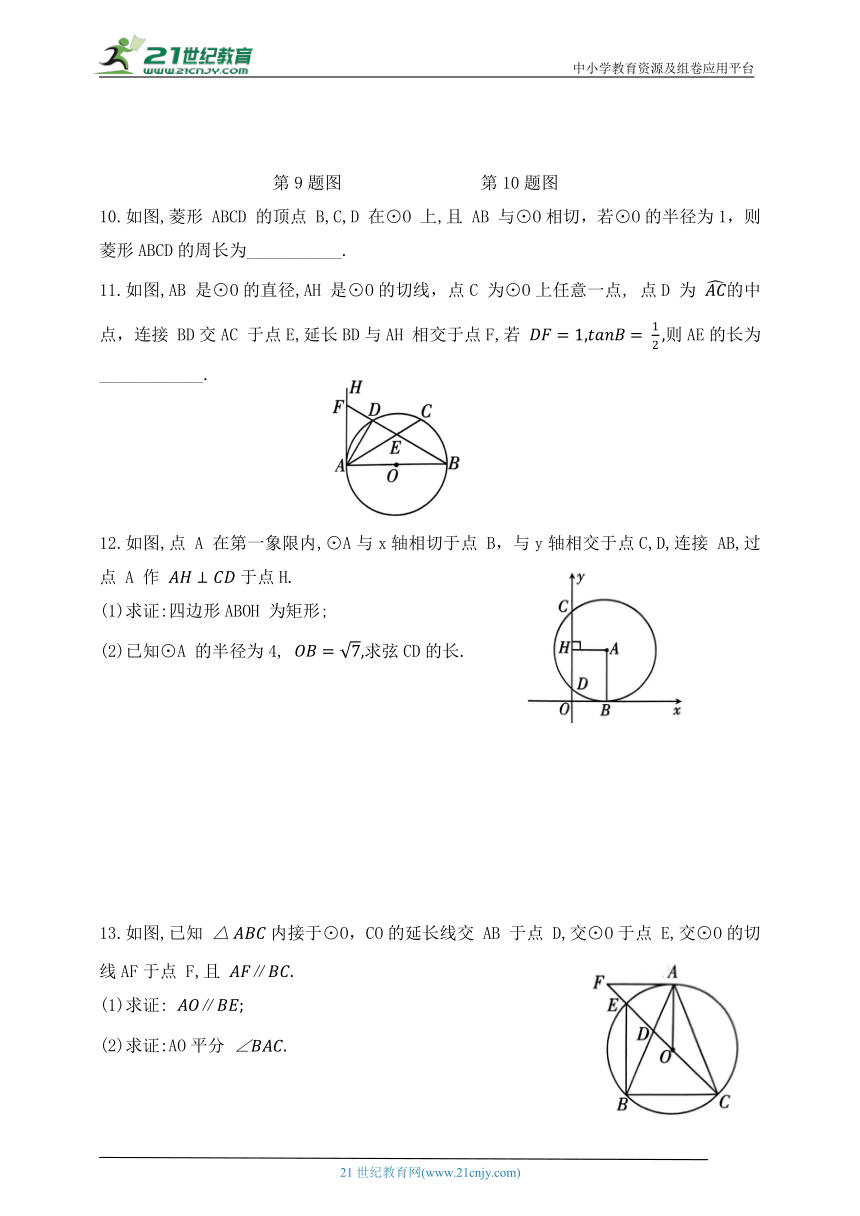
5.如图所示,某宾馆大厅要铺圆环形的地毯,工人师傅只测量了与小圆相切的大圆的弦AB的长,就计算出了圆环的面积.若测量得到AB的长为20 m,则圆环的面积为 ( )
第5题图 第6题图
6.如图,四边形 ABCD是⊙O的内接四边形,AB是⊙O的直径,过点 D 的切线交 BA 的延长线于点 E,若则∠C的度数是 ( )
A. 152° B. 134° C. 124°
7.如图,在平面直角坐标系中,点A, B在函数的图象上,分别以A,B为圆心,1为半径作圆,当⊙A 与x轴相切,⊙B 与y轴相切时,连接 AB, 则k的值为 ( )
8.如图,三角板、量角器和直尺如图摆放,三角板的斜边 BC与半圆O相切于点C,点B,D,E分别与直尺的刻度1,9,19 重合,则三角板直角边 AC 的长为 ( )
9.如图,CD 是⊙O的切线,点C 在直径的延长线上,若
第9题图 第10题图
10.如图,菱形 ABCD 的顶点 B,C,D 在⊙O 上,且 AB 与⊙O相切,若⊙O的半径为1,则菱形ABCD的周长为___________.
11.如图,AB 是⊙O的直径,AH 是⊙O的切线,点C 为⊙O上任意一点, 点D 为 的中点,连接 BD交AC 于点E,延长BD与AH 相交于点F,若 则AE的长为____________.
12.如图,点 A 在第一象限内,⊙A与x轴相切于点 B,与y轴相交于点C,D,连接 AB,过点 A 作 于点H.
(1)求证:四边形ABOH 为矩形;
(2)已知⊙A 的半径为4, 求弦CD的长.
13.如图,已知 内接于⊙O,CO的延长线交 AB 于点 D,交⊙O于点 E,交⊙O的切线AF于点 F,且 ∥
(1)求证: ∥
(2)求证:AO平分
14.如图,AB为半圆O 的直径,点 F 在半圆上,点P 在 AB 的延长线上,PC与半圆相切于点C,与OF 的延长线相交于点 D,AC 与OF 相交于点 E, DE.
(1)写出图中一个与 相等的角:___________;
(2)求证:
(3)若 求PB的长.
15.如图,在平面直角坐标系中,点 P 在第一象限内,⊙P 与x 轴相切于点C,与 y轴相交于点 A(0,8),B(0,2).连接AC,BC.
(1)求点 P 的坐标;
(2)求 的值.
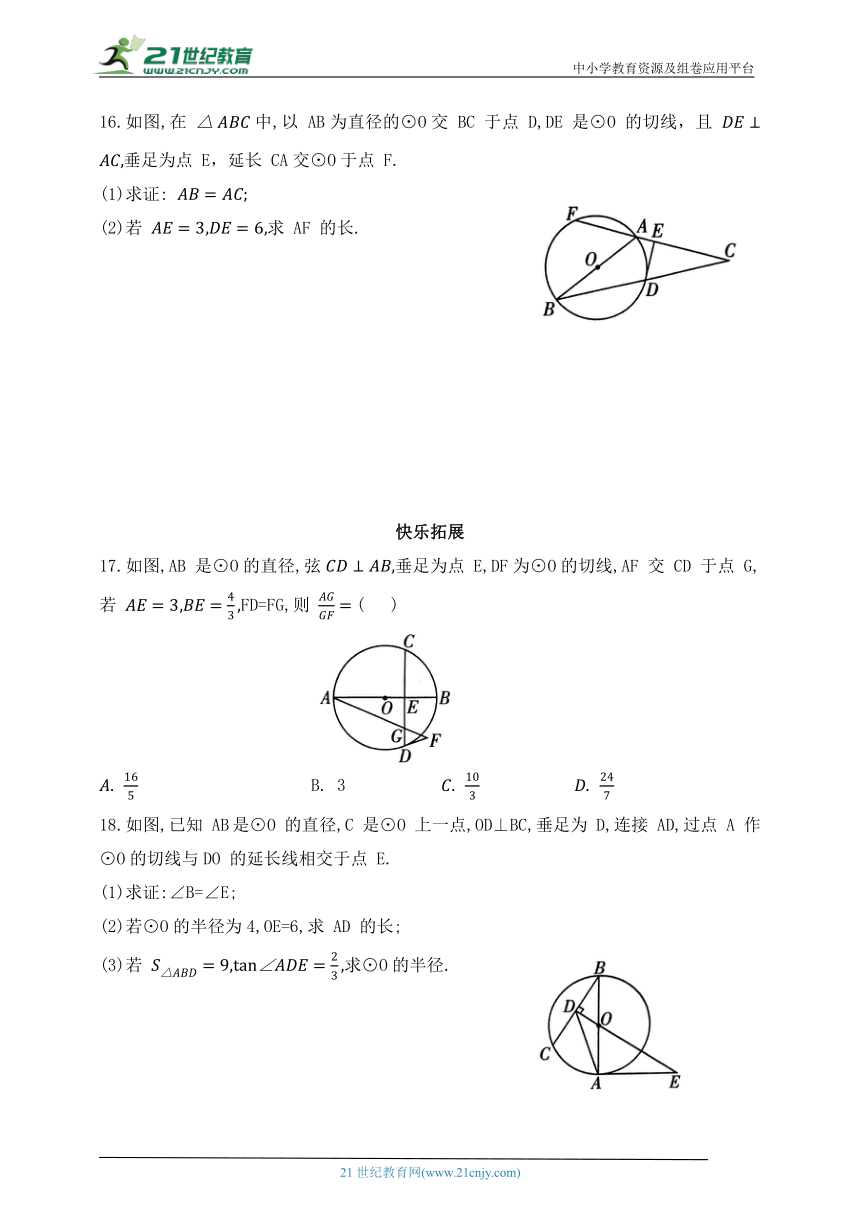
16.如图,在 中,以 AB为直径的⊙O交 BC 于点 D,DE 是⊙O 的切线,且 垂足为点 E,延长 CA交⊙O于点 F.
(1)求证:
(2)若 求 AF 的长.
快乐拓展
17.如图,AB 是⊙O的直径,弦垂足为点 E,DF为⊙O的切线,AF 交 CD 于点 G,若 FD=FG,则 ( )
B. 3
18.如图,已知 AB是⊙O 的直径,C 是⊙O 上一点,OD⊥BC,垂足为 D,连接 AD,过点 A 作⊙O的切线与DO 的延长线相交于点 E.
(1)求证:∠B=∠E;
(2)若⊙O的半径为4,OE=6,求 AD 的长;
(3)若 求⊙O的半径.
参考答案
1. C 2. A 3. B 4. C 5. D 6. D 7. C 8. D
9. 2
12.解:(1)证明:∵⊙A 与x轴相切于点 B, ∴AB⊥x轴,
又∵AH⊥CD,HO⊥OB,∴∠AHO=∠HOB=∠OBA=90°,
∴四边形 ABOH 是矩形;
(2)连接AD,
∵四边形 ABOH 是矩形,
∵AD=AB=4,3,
∵AH⊥CD,∴CD=2DH=6.
13.证明:(1)∵AF 是⊙O的切线,∴AF⊥OA,即∠OAF=90°,
∵CE是⊙O的直径,∴∠CBE=90°,∴∠OAF=∠CBE,
∵AF∥BC,∴∠BAF=∠ABC,
∴∠OAF-∠BAF=∠CBE-∠ABC,即∠OAB=∠ABE,∴AO∥BE;
(2)∵OA=OC,∴∠ACE=∠OAC,
∵∠ABE=∠ACE,∴∠ABE=∠OAC,
由(1),得EB∥AO,∴∠OAB=∠ABE,∴∠OAB=∠OAC,∴AO平分∠BAC.
14.解:(1)∵DC=DE,∴∠DCE=∠DEC.
故答案为:∠DCE(答案不唯一);
(2)证明:连接OC,
∵PC是切线,∴OC⊥CD,即∠DCE+∠ACO=90°.
∵OA=OC,∴∠OAC=∠ACO.
∵∠DCE=∠DEC,∠AEO=∠DEC,∴∠AEO+∠CAO=90°.∴∠AOE=90°,∴OD⊥AB;
(3)设OE=x,则 AO=OF=BO=2x,∴EF=OF-OE=x,OD=OF+DF=2x+2,
∴DC=DE=DF+EF=2+x.
在 Rt△ODC 中,
解得 (舍去),∴OD=10,CD=6,OC=8.
解得
15.解:(1)∵点 A(0,8),B(0,2),
过点 P 作 于点H,
连接 PC,PB,
∵⊙P 与x轴相切于点C, 轴,
∴四边形 PCOH 是矩形,
在 中, ∴点 P 的坐标为(4,5);
(2)连接AP并延长,交⊙P 于点 M,连接BM,则∠ABM=90°,AM=10,
16.解:(1)证明:连接OD,
∵DE 是⊙O的切线,∴OD⊥DE,
∵DE⊥AC,∴OD∥AC,∴∠C=∠ODB,
∵OD=OB,∴∠B=∠ODB,∴∠B=∠C,∴AB=AC;
(2)连接 DF,DA,
∵∠F=∠B,∠B=∠C,∴∠F=∠C,∴DF=DC,
∵DE⊥CF,∴FE=EC,
∵AB 是圆的直径,∴∠ADB=90°,∴∠ADC=90°,∴∠ADE+∠CDE=90°,
∵DE⊥AC,∴∠C+∠CDE=90°,
17. C解析:连接OD,
∴⊙O的半径
∵CD⊥AB,即∠AED=90°,
∴在 Rt△ODE 中,
∵DF是⊙O的切线,∴OD⊥DF.∴∠ODF=90°,即∠ODE+∠CDF=90°.
∵∠AEG=90°,∴∠EAG+∠AGE=90°.
∵FD=FG,∴∠CDF=∠FGD=∠AGE.∴∠EAG=∠EDO.
∵∠AEG=∠DEO=90°,∴△AEG∽△DEO. 即
过点 F作FM⊥CD于点 M,
∵FD=FG,
∵∠AGE=∠FGM,∠AEG=∠GMF=90°,∴△AEG∽△FMG.
18.解:(1)证明:∵OD⊥BC,垂足为 D, ∴∠ODB=90°.
∵过点 A 作⊙O 的切线与 DO 的延长线相交于点E,∴∠OAE=90°.
∵∠BOD=∠AOE,∵∠B=180°-(∠BOD+∠ODB)=90°-∠BOD,∠E=180°-(∠OAE+∠AOE)=90°-∠AOE,∴∠B=∠E;
(2)连接AC,OC,
∵∠BOD=∠AOE,∠B=∠E,∴△BOD∽△EOA,
∵OA=4,OE=6,∴在 Rt△OAE中,
∵OD⊥BC,垂足为 D,OB=OC,
∵AB是⊙O的直径,AB=8,∴∠ACB=90°.
∴在 Rt△ABC中,
∴在 中,
∴AD的长为
(3)∵AB是⊙O的直径, ∴AC∥ED,
∴∠CAD=∠ADE,
设AC=3x,则(
由S△ABD=9, 得 解得
即⊙O的半径为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
6 直线和圆的位置关系
第2课时 切线的性质
轻松过关
1.如图,在⊙O中,CD切⊙O于点 C,若 则 的大小为 ( )
第1题图 第2题图
2.如图,⊙O 是等边的外接圆,过点 A 作⊙O的切线交BO 的延长线于点 D,若OB=1,则 OD 的长为 ( )
A. 2 B. 3
3.当宽为3 cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为 ( )
第3题图 第4题图
4.如图,AB是圆O的直径,弦AD平分∠BAC,过点 D 的切线交 AC 于点 E,则下列结论错误的是 ( )
∥
5.如图所示,某宾馆大厅要铺圆环形的地毯,工人师傅只测量了与小圆相切的大圆的弦AB的长,就计算出了圆环的面积.若测量得到AB的长为20 m,则圆环的面积为 ( )
第5题图 第6题图
6.如图,四边形 ABCD是⊙O的内接四边形,AB是⊙O的直径,过点 D 的切线交 BA 的延长线于点 E,若则∠C的度数是 ( )
A. 152° B. 134° C. 124°
7.如图,在平面直角坐标系中,点A, B在函数的图象上,分别以A,B为圆心,1为半径作圆,当⊙A 与x轴相切,⊙B 与y轴相切时,连接 AB, 则k的值为 ( )
8.如图,三角板、量角器和直尺如图摆放,三角板的斜边 BC与半圆O相切于点C,点B,D,E分别与直尺的刻度1,9,19 重合,则三角板直角边 AC 的长为 ( )
9.如图,CD 是⊙O的切线,点C 在直径的延长线上,若
第9题图 第10题图
10.如图,菱形 ABCD 的顶点 B,C,D 在⊙O 上,且 AB 与⊙O相切,若⊙O的半径为1,则菱形ABCD的周长为___________.
11.如图,AB 是⊙O的直径,AH 是⊙O的切线,点C 为⊙O上任意一点, 点D 为 的中点,连接 BD交AC 于点E,延长BD与AH 相交于点F,若 则AE的长为____________.
12.如图,点 A 在第一象限内,⊙A与x轴相切于点 B,与y轴相交于点C,D,连接 AB,过点 A 作 于点H.
(1)求证:四边形ABOH 为矩形;
(2)已知⊙A 的半径为4, 求弦CD的长.
13.如图,已知 内接于⊙O,CO的延长线交 AB 于点 D,交⊙O于点 E,交⊙O的切线AF于点 F,且 ∥
(1)求证: ∥
(2)求证:AO平分
14.如图,AB为半圆O 的直径,点 F 在半圆上,点P 在 AB 的延长线上,PC与半圆相切于点C,与OF 的延长线相交于点 D,AC 与OF 相交于点 E, DE.
(1)写出图中一个与 相等的角:___________;
(2)求证:
(3)若 求PB的长.
15.如图,在平面直角坐标系中,点 P 在第一象限内,⊙P 与x 轴相切于点C,与 y轴相交于点 A(0,8),B(0,2).连接AC,BC.
(1)求点 P 的坐标;
(2)求 的值.
16.如图,在 中,以 AB为直径的⊙O交 BC 于点 D,DE 是⊙O 的切线,且 垂足为点 E,延长 CA交⊙O于点 F.
(1)求证:
(2)若 求 AF 的长.
快乐拓展
17.如图,AB 是⊙O的直径,弦垂足为点 E,DF为⊙O的切线,AF 交 CD 于点 G,若 FD=FG,则 ( )
B. 3
18.如图,已知 AB是⊙O 的直径,C 是⊙O 上一点,OD⊥BC,垂足为 D,连接 AD,过点 A 作⊙O的切线与DO 的延长线相交于点 E.
(1)求证:∠B=∠E;
(2)若⊙O的半径为4,OE=6,求 AD 的长;
(3)若 求⊙O的半径.
参考答案
1. C 2. A 3. B 4. C 5. D 6. D 7. C 8. D
9. 2
12.解:(1)证明:∵⊙A 与x轴相切于点 B, ∴AB⊥x轴,
又∵AH⊥CD,HO⊥OB,∴∠AHO=∠HOB=∠OBA=90°,
∴四边形 ABOH 是矩形;
(2)连接AD,
∵四边形 ABOH 是矩形,
∵AD=AB=4,3,
∵AH⊥CD,∴CD=2DH=6.
13.证明:(1)∵AF 是⊙O的切线,∴AF⊥OA,即∠OAF=90°,
∵CE是⊙O的直径,∴∠CBE=90°,∴∠OAF=∠CBE,
∵AF∥BC,∴∠BAF=∠ABC,
∴∠OAF-∠BAF=∠CBE-∠ABC,即∠OAB=∠ABE,∴AO∥BE;
(2)∵OA=OC,∴∠ACE=∠OAC,
∵∠ABE=∠ACE,∴∠ABE=∠OAC,
由(1),得EB∥AO,∴∠OAB=∠ABE,∴∠OAB=∠OAC,∴AO平分∠BAC.
14.解:(1)∵DC=DE,∴∠DCE=∠DEC.
故答案为:∠DCE(答案不唯一);
(2)证明:连接OC,
∵PC是切线,∴OC⊥CD,即∠DCE+∠ACO=90°.
∵OA=OC,∴∠OAC=∠ACO.
∵∠DCE=∠DEC,∠AEO=∠DEC,∴∠AEO+∠CAO=90°.∴∠AOE=90°,∴OD⊥AB;
(3)设OE=x,则 AO=OF=BO=2x,∴EF=OF-OE=x,OD=OF+DF=2x+2,
∴DC=DE=DF+EF=2+x.
在 Rt△ODC 中,
解得 (舍去),∴OD=10,CD=6,OC=8.
解得
15.解:(1)∵点 A(0,8),B(0,2),
过点 P 作 于点H,
连接 PC,PB,
∵⊙P 与x轴相切于点C, 轴,
∴四边形 PCOH 是矩形,
在 中, ∴点 P 的坐标为(4,5);
(2)连接AP并延长,交⊙P 于点 M,连接BM,则∠ABM=90°,AM=10,
16.解:(1)证明:连接OD,
∵DE 是⊙O的切线,∴OD⊥DE,
∵DE⊥AC,∴OD∥AC,∴∠C=∠ODB,
∵OD=OB,∴∠B=∠ODB,∴∠B=∠C,∴AB=AC;
(2)连接 DF,DA,
∵∠F=∠B,∠B=∠C,∴∠F=∠C,∴DF=DC,
∵DE⊥CF,∴FE=EC,
∵AB 是圆的直径,∴∠ADB=90°,∴∠ADC=90°,∴∠ADE+∠CDE=90°,
∵DE⊥AC,∴∠C+∠CDE=90°,
17. C解析:连接OD,
∴⊙O的半径
∵CD⊥AB,即∠AED=90°,
∴在 Rt△ODE 中,
∵DF是⊙O的切线,∴OD⊥DF.∴∠ODF=90°,即∠ODE+∠CDF=90°.
∵∠AEG=90°,∴∠EAG+∠AGE=90°.
∵FD=FG,∴∠CDF=∠FGD=∠AGE.∴∠EAG=∠EDO.
∵∠AEG=∠DEO=90°,∴△AEG∽△DEO. 即
过点 F作FM⊥CD于点 M,
∵FD=FG,
∵∠AGE=∠FGM,∠AEG=∠GMF=90°,∴△AEG∽△FMG.
18.解:(1)证明:∵OD⊥BC,垂足为 D, ∴∠ODB=90°.
∵过点 A 作⊙O 的切线与 DO 的延长线相交于点E,∴∠OAE=90°.
∵∠BOD=∠AOE,∵∠B=180°-(∠BOD+∠ODB)=90°-∠BOD,∠E=180°-(∠OAE+∠AOE)=90°-∠AOE,∴∠B=∠E;
(2)连接AC,OC,
∵∠BOD=∠AOE,∠B=∠E,∴△BOD∽△EOA,
∵OA=4,OE=6,∴在 Rt△OAE中,
∵OD⊥BC,垂足为 D,OB=OC,
∵AB是⊙O的直径,AB=8,∴∠ACB=90°.
∴在 Rt△ABC中,
∴在 中,
∴AD的长为
(3)∵AB是⊙O的直径, ∴AC∥ED,
∴∠CAD=∠ADE,
设AC=3x,则(
由S△ABD=9, 得 解得
即⊙O的半径为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
