6.4随机现象的变化趋势(同步课件)(共29张PPT) -2024-2025学年九年级数学下册(青岛版)
文档属性
| 名称 | 6.4随机现象的变化趋势(同步课件)(共29张PPT) -2024-2025学年九年级数学下册(青岛版) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 19:39:31 | ||
图片预览








文档简介
(共29张PPT)
6.4 随机现象的变化趋势
主讲:
青岛版9年级数学下册
第6章 事件的概率
学习目标
目标
1
1.通过探究青春身高与体重的关系,感受一些客观存在随机现象规律;
2.会用平面直角坐标系中的点表示两个变量之间的关系;
3.能够运用随机规律解决一些实际问题.
重点
2
难点
3
利用随机现象规律判断变化趋势
掌握随机现象的特点
新课导入
著名的英国生物学家、统计学家高尔顿最早针对变量之间的关系的做了研究.1877年,他在研究人类身高的遗传问题时,发现矮个子父亲的儿子平场身高往往比父辈高,但比本种族的平均身高矮;高个子父亲的儿子平均身高比父辈矮,但高于本种族的平均身高.由此他得到儿子的身高有返回本种族平均身高的趋势.他把达一现象称为“回归”,后来又引进了线性回归、非线性回归等。
你知道其中的规律吗?
新课导入
在此之前,我们学过的一次函数,反比例函数,二次函数都是刻画客观世界中相互联系的变量之间关系的模型。
你认为青少年的身高和体重有关系吗?如果有,它们之间的关系是正比例关系吗?是函数关系吗?
请同学们思考本班的同学的身高与体重的关系是否是函数关系,并与同伴交流.
新课讲授
(1)你认为青少年的身高与体重有关系吗?如果有,它们之间的关系是正比例关系吗?是函数关系吗?
为了研究这个问题,九年级一班数学兴趣小组随机抽取了本班13名男生,测量出他们的身高(单位:cm)和体重(单位:kg),得到了下表中的两组数据:
身高/cm 153 147 153 145 170 174 165 170 159 180 172 162 170
体重/kg 41 45 48 42 60 71 52 64 56 68 67 48 51
(2)为了研究这个样本的身高和体重之间的关系,怎样才能将上表中的两组数据直观地表示出来呢?与同学交流.
新课讲授
能把每人的身高和体重分别作为点的坐标,在直角坐标系中描出对应的各点,然后通过观察这些点的分布情况探究它们之间的关系吗?
如果要建立直角坐标系,怎样确定横轴和纵轴所代表的意义以及它们的度量单位呢?
怎么办?
怎么办?
新课讲授
(3)分别找出表中身高与体重数据的最大值和最小值,你能由此确定13名男生身高与体重的范围吗?这对于我们画出直角坐标系有什么帮助呢?
上表中这些男生的身高范围是145 cm ~ 180 cm,体重范围是41 kg ~ 71 kg. 可以设想,在画直角坐标系时,应当适当选择度量单位,使身高和体重的范围在坐标轴上的位置居中,从而使根据表中的数据描出的各点,离坐标轴不至于87太远,以便于观察. 对于这些范围之外的部分,由于没有已知的数据,不必留出过多空间.
新课讲授
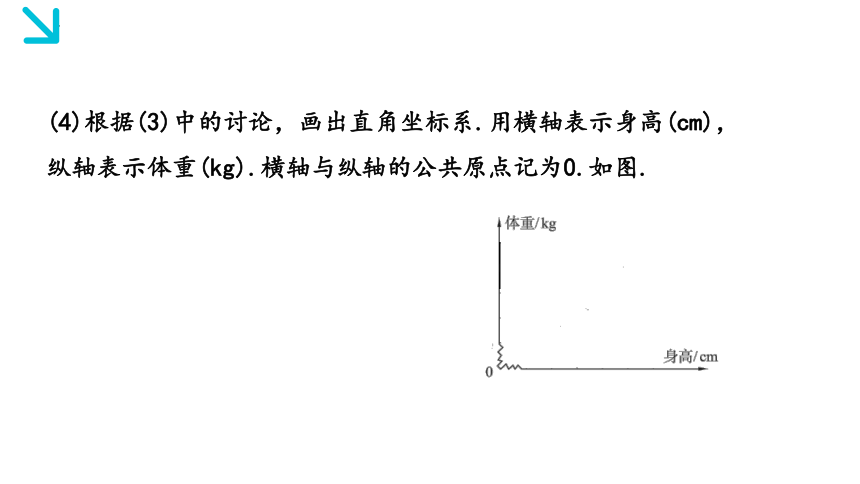
(4)根据(3)中的讨论,画出直角坐标系.用横轴表示身高(cm),纵轴表示体重(kg).横轴与纵轴的公共原点记为0.如图.
新课讲授
因为13名学生的身高数据的范围是145cm~180cm,可在横轴上先标出了一个比它略大一些的范围140cm~190cm.确定范围的端点后,将该线段5等分.将各分点自左向右依次标上刻度140,150,160,170,180,190.在纵轴上标记出40,50,60,70,80. 在两个坐标轴上,0与横轴上的刻度140以及纵轴上刻度40之间的部分通常画成破格线,以表示数值的连接.如图.
新课讲授
5.在画出的直角坐标系中,将每位男生的身高和体重数据作为一个有序数对,在坐标系中,描出13个有序数对所对应的点.如图.
提分笔记
注意:在图中,两个坐标轴的单位长度不同,表示的意义也不同.但是只要刻度之间的比例关系一致,坐标系中的点所表达的意义就是合理的.因此,在确定坐标轴的单位长度时,要注意具体问题具体分析.
新课讲授
(1)观察右图,找出样本中个子最高的同学所对应的点,他的体重是多少?他的体重是样本中最重的吗?个子最矮的同学的体重是多少?他的体重是样本中最轻的吗?
(2)在上述样本中,有没有身高相同的同学?如果有,他们的体重也相同吗?在直角坐标系中,你发现他们的数据所对应的点有什么特征?
新课讲授
我发现身高170cm的有三位同学,他们的体重分别是51kg,60kg,64kg.看来身高并不能确定体重,因此体重与身高之间不是函数关系.
如果把身高看作是一组随机变化的量,体重与身高之间有什么关系呢?
新课讲授
在上面的问题中,如果把样本的身高看作一组随机变化的量,将样本的身高按从小到大的顺序排列,从图中可以看出样本的体重与身高之间具有某种相关关系.这些点的位置具有一定的随机性,但大体上分布在一个带形区域内. 这就是说,这些男生的体重与身高之间的关系虽然不是函数关系,但随机抽样的数据显示,二者之间并非毫无关联,而有一定的规律,即体重随着身高的增加呈现一种线性的增长趋势.
提分笔记
新课讲授
(3)在右图中,怎样用一条直线近似地表示体重随身高的增长趋势?
小亮和小莹在右图中分别画出了直线a 和b.比较他们所画出的直线,你认为哪条直线更合适一些?
新课讲授
由于画出的直线只是近似地表示图中各点的变化趋势,所以实际上还可以画出很多条直线,有没有比直线b更“合适”的直线?怎样比较精确地确定“合适”的直线?这类问题将在高中阶段的学习中去解决.
这样的描述精确吗?
新课讲授
一方面,对于直线a来说,有10个点在它的上方,有3个点在它的下方;而对于直线b,有7个点在它的上方,6个点在它的下方;另一方面,各点到直线b的距离整体上比到直线a的距离要小.相比而言,直线b要比直线a更合适.
提分笔记
典例分析
三大
特点
例1
某超市随机抽取了12天的日利润与日营业额,如下表所示:
日营业额/万元 14.1 5.1 8.0 7.2 5.8 12.3 9.8 10.8 9.3 15.1 4.2 13.2
日利润/万元 2.8 1.0 1.4 1.3 1.4 2.2 2.0 1.8 1.9 2.3 1.1 2.3
(1)在直角坐标系中,用横轴表示日营业额、纵轴表示日利润,描出上述12个数对对应的数据点;
(2)在坐标系中,画出一条直线,使它能近似地反映样本中日利润与日营业额的相关关系;
典例分析
三大
特点
(3)估计这家超市的日营业额为16万元时,日利润大约多少万元?
解:
(1)将12对数据对应的点描在如右图所示的直角坐标系中:
典例分析
三大
特点
(2)在这个坐标系中画出一条较“合适” 的直线.
典例分析
三大
特点
(3)在这条直线上取横坐标为16的点,其纵坐标为2.8.所以由此估计当这家超市日营业额为16万元时,日利润约为2.8万元.
学以致用
1.如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.下面有三个推断:①某次实验投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616;②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.其中合理的是( )
A.①② B.②③
C.①③ D.①②③
A
学以致用
2.下图是某市交通事故统计图,看过此图后,用一句话表达你的感想 .
交通事故危害生命,安全驾驶,减少事故发生(答案不唯一)
学以致用
3.下表是小强爸爸在某年10月购买某股票所付的钱数(单位:元)与所赚金额(单位:元):
所付钱数 500 1000 1500 2000 3000 3500 4500
赚到的金额 100 250 150 50 500 300 1000
请你分析小强的爸爸在10月购买某股票所付的钱数(单位:元)与所赚金额(单位:元)之间的变化趋势.
学以致用
解:先画出的平面直角坐标,并在平面直角坐标系中描述各个点,再画出直线,如图所示:
∴根据横坐标所付钱数即可得到纵坐标所赚钱数的关系.
学以致用
3.一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的 反面是平的.将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是 “兵”面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的机会大小,某 实验小组做了棋子下掷实验,实验数据如下表:
实验次数 20 40 60 80 100 120 140 160
“兵”字面朝上频数 14 38 47 52 66 78 88
“兵”字面朝上频率 0.7 0.45 0.63 0.59 0.52 0.56 0.55
(1)请将数据表补充完整:
(2)在图中画出“兵”字面朝上的频率分布折线图:
(3)如果实验继续进行下去,根据上表的数据,这个实验所得频率将逐渐稳定到某 一个数值附近,请你估计该随机事件在每次实验时发生的机会大小.
学以致用
解:(1)所填数字为:40×0.45=18,66÷120=0.55;
∴答案为18,0.55;
(2)折线图如下:
(3)根据表中数据,试验频率为0.7,0.45,0.63,0.59,0.52,0.55,0.56,0.55稳定在0.55左右,
∴估计概率的大小为:0.55.
学后总结
随机现象的变化趋势
在直角坐标系中描述出各点后,各点分布在一个带形区域内,说明两个变量之间呈现一种线性关系,可以画一条直线近似表示各点之间的变化趋势,近似表示两个变量之间的关系.
2. 用一条直线表示
把两个变量的每一对数值分别作为点的坐标,在直角坐标系中描述出各个点,观察这些点的分布情况,探究得到两个量之间的关系.
1.用直角坐标系中的点表示
课堂小结
1.今天你的收获是什么?
2.还有什么疑惑?
主讲:
青岛版9年级数学下册
感谢聆听
6.4 随机现象的变化趋势
主讲:
青岛版9年级数学下册
第6章 事件的概率
学习目标
目标
1
1.通过探究青春身高与体重的关系,感受一些客观存在随机现象规律;
2.会用平面直角坐标系中的点表示两个变量之间的关系;
3.能够运用随机规律解决一些实际问题.
重点
2
难点
3
利用随机现象规律判断变化趋势
掌握随机现象的特点
新课导入
著名的英国生物学家、统计学家高尔顿最早针对变量之间的关系的做了研究.1877年,他在研究人类身高的遗传问题时,发现矮个子父亲的儿子平场身高往往比父辈高,但比本种族的平均身高矮;高个子父亲的儿子平均身高比父辈矮,但高于本种族的平均身高.由此他得到儿子的身高有返回本种族平均身高的趋势.他把达一现象称为“回归”,后来又引进了线性回归、非线性回归等。
你知道其中的规律吗?
新课导入
在此之前,我们学过的一次函数,反比例函数,二次函数都是刻画客观世界中相互联系的变量之间关系的模型。
你认为青少年的身高和体重有关系吗?如果有,它们之间的关系是正比例关系吗?是函数关系吗?
请同学们思考本班的同学的身高与体重的关系是否是函数关系,并与同伴交流.
新课讲授
(1)你认为青少年的身高与体重有关系吗?如果有,它们之间的关系是正比例关系吗?是函数关系吗?
为了研究这个问题,九年级一班数学兴趣小组随机抽取了本班13名男生,测量出他们的身高(单位:cm)和体重(单位:kg),得到了下表中的两组数据:
身高/cm 153 147 153 145 170 174 165 170 159 180 172 162 170
体重/kg 41 45 48 42 60 71 52 64 56 68 67 48 51
(2)为了研究这个样本的身高和体重之间的关系,怎样才能将上表中的两组数据直观地表示出来呢?与同学交流.
新课讲授
能把每人的身高和体重分别作为点的坐标,在直角坐标系中描出对应的各点,然后通过观察这些点的分布情况探究它们之间的关系吗?
如果要建立直角坐标系,怎样确定横轴和纵轴所代表的意义以及它们的度量单位呢?
怎么办?
怎么办?
新课讲授
(3)分别找出表中身高与体重数据的最大值和最小值,你能由此确定13名男生身高与体重的范围吗?这对于我们画出直角坐标系有什么帮助呢?
上表中这些男生的身高范围是145 cm ~ 180 cm,体重范围是41 kg ~ 71 kg. 可以设想,在画直角坐标系时,应当适当选择度量单位,使身高和体重的范围在坐标轴上的位置居中,从而使根据表中的数据描出的各点,离坐标轴不至于87太远,以便于观察. 对于这些范围之外的部分,由于没有已知的数据,不必留出过多空间.
新课讲授
(4)根据(3)中的讨论,画出直角坐标系.用横轴表示身高(cm),纵轴表示体重(kg).横轴与纵轴的公共原点记为0.如图.
新课讲授
因为13名学生的身高数据的范围是145cm~180cm,可在横轴上先标出了一个比它略大一些的范围140cm~190cm.确定范围的端点后,将该线段5等分.将各分点自左向右依次标上刻度140,150,160,170,180,190.在纵轴上标记出40,50,60,70,80. 在两个坐标轴上,0与横轴上的刻度140以及纵轴上刻度40之间的部分通常画成破格线,以表示数值的连接.如图.
新课讲授
5.在画出的直角坐标系中,将每位男生的身高和体重数据作为一个有序数对,在坐标系中,描出13个有序数对所对应的点.如图.
提分笔记
注意:在图中,两个坐标轴的单位长度不同,表示的意义也不同.但是只要刻度之间的比例关系一致,坐标系中的点所表达的意义就是合理的.因此,在确定坐标轴的单位长度时,要注意具体问题具体分析.
新课讲授
(1)观察右图,找出样本中个子最高的同学所对应的点,他的体重是多少?他的体重是样本中最重的吗?个子最矮的同学的体重是多少?他的体重是样本中最轻的吗?
(2)在上述样本中,有没有身高相同的同学?如果有,他们的体重也相同吗?在直角坐标系中,你发现他们的数据所对应的点有什么特征?
新课讲授
我发现身高170cm的有三位同学,他们的体重分别是51kg,60kg,64kg.看来身高并不能确定体重,因此体重与身高之间不是函数关系.
如果把身高看作是一组随机变化的量,体重与身高之间有什么关系呢?
新课讲授
在上面的问题中,如果把样本的身高看作一组随机变化的量,将样本的身高按从小到大的顺序排列,从图中可以看出样本的体重与身高之间具有某种相关关系.这些点的位置具有一定的随机性,但大体上分布在一个带形区域内. 这就是说,这些男生的体重与身高之间的关系虽然不是函数关系,但随机抽样的数据显示,二者之间并非毫无关联,而有一定的规律,即体重随着身高的增加呈现一种线性的增长趋势.
提分笔记
新课讲授
(3)在右图中,怎样用一条直线近似地表示体重随身高的增长趋势?
小亮和小莹在右图中分别画出了直线a 和b.比较他们所画出的直线,你认为哪条直线更合适一些?
新课讲授
由于画出的直线只是近似地表示图中各点的变化趋势,所以实际上还可以画出很多条直线,有没有比直线b更“合适”的直线?怎样比较精确地确定“合适”的直线?这类问题将在高中阶段的学习中去解决.
这样的描述精确吗?
新课讲授
一方面,对于直线a来说,有10个点在它的上方,有3个点在它的下方;而对于直线b,有7个点在它的上方,6个点在它的下方;另一方面,各点到直线b的距离整体上比到直线a的距离要小.相比而言,直线b要比直线a更合适.
提分笔记
典例分析
三大
特点
例1
某超市随机抽取了12天的日利润与日营业额,如下表所示:
日营业额/万元 14.1 5.1 8.0 7.2 5.8 12.3 9.8 10.8 9.3 15.1 4.2 13.2
日利润/万元 2.8 1.0 1.4 1.3 1.4 2.2 2.0 1.8 1.9 2.3 1.1 2.3
(1)在直角坐标系中,用横轴表示日营业额、纵轴表示日利润,描出上述12个数对对应的数据点;
(2)在坐标系中,画出一条直线,使它能近似地反映样本中日利润与日营业额的相关关系;
典例分析
三大
特点
(3)估计这家超市的日营业额为16万元时,日利润大约多少万元?
解:
(1)将12对数据对应的点描在如右图所示的直角坐标系中:
典例分析
三大
特点
(2)在这个坐标系中画出一条较“合适” 的直线.
典例分析
三大
特点
(3)在这条直线上取横坐标为16的点,其纵坐标为2.8.所以由此估计当这家超市日营业额为16万元时,日利润约为2.8万元.
学以致用
1.如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.下面有三个推断:①某次实验投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616;②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.其中合理的是( )
A.①② B.②③
C.①③ D.①②③
A
学以致用
2.下图是某市交通事故统计图,看过此图后,用一句话表达你的感想 .
交通事故危害生命,安全驾驶,减少事故发生(答案不唯一)
学以致用
3.下表是小强爸爸在某年10月购买某股票所付的钱数(单位:元)与所赚金额(单位:元):
所付钱数 500 1000 1500 2000 3000 3500 4500
赚到的金额 100 250 150 50 500 300 1000
请你分析小强的爸爸在10月购买某股票所付的钱数(单位:元)与所赚金额(单位:元)之间的变化趋势.
学以致用
解:先画出的平面直角坐标,并在平面直角坐标系中描述各个点,再画出直线,如图所示:
∴根据横坐标所付钱数即可得到纵坐标所赚钱数的关系.
学以致用
3.一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的 反面是平的.将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是 “兵”面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的机会大小,某 实验小组做了棋子下掷实验,实验数据如下表:
实验次数 20 40 60 80 100 120 140 160
“兵”字面朝上频数 14 38 47 52 66 78 88
“兵”字面朝上频率 0.7 0.45 0.63 0.59 0.52 0.56 0.55
(1)请将数据表补充完整:
(2)在图中画出“兵”字面朝上的频率分布折线图:
(3)如果实验继续进行下去,根据上表的数据,这个实验所得频率将逐渐稳定到某 一个数值附近,请你估计该随机事件在每次实验时发生的机会大小.
学以致用
解:(1)所填数字为:40×0.45=18,66÷120=0.55;
∴答案为18,0.55;
(2)折线图如下:
(3)根据表中数据,试验频率为0.7,0.45,0.63,0.59,0.52,0.55,0.56,0.55稳定在0.55左右,
∴估计概率的大小为:0.55.
学后总结
随机现象的变化趋势
在直角坐标系中描述出各点后,各点分布在一个带形区域内,说明两个变量之间呈现一种线性关系,可以画一条直线近似表示各点之间的变化趋势,近似表示两个变量之间的关系.
2. 用一条直线表示
把两个变量的每一对数值分别作为点的坐标,在直角坐标系中描述出各个点,观察这些点的分布情况,探究得到两个量之间的关系.
1.用直角坐标系中的点表示
课堂小结
1.今天你的收获是什么?
2.还有什么疑惑?
主讲:
青岛版9年级数学下册
感谢聆听
