第六章 特殊的平行四边形检测题(含答案)
文档属性
| 名称 | 第六章 特殊的平行四边形检测题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 568.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-18 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八年级数学(下)第六章 特殊平行四边形检测题
一、选择题(共10个小题,每题5分)
1.关于四边形,下列说法正确的是( )
A.对角线相等的是矩形 B.对角线互相垂直的是菱形
C.对角线互相垂直且相等的是正方形 D.对角线互相平分的是平行四边形
2.在四边形ABCD中,两对角线交于点O,若OA=OB=OC=OD,则这个四边形( )
A.可能不是平行四边形 B.一定是菱形
C.一定是正方形 D.一定是矩形
3.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的( )
A. B. C. D.
4.如图,点E在正方形ABCD的对角线AC上,若AE=AB,则∠EBC的度数为( )
A.22.5° B.30° C.45° D.67.5°
5.如图,在平面直角坐标系中,菱形ABCD的顶点A在y轴上,顶点B,C的坐标分别为(﹣6,0),(4,0),则点D的坐标是( )
A.(6,8) B.(10,8) C.(10,6) D.(4,6)
(
6题图
) (
3题图
)
(
5题图
) (
4题图
)
6.如图.在正方形中,点在对角线上,,,,分别为垂足,连接,,则下列命题:①若,则:②若正方形边长为4,则的最小值为2:③若,则,其中正确的命题是( )
A.①② B.①③ C.②③ D.①②③
如图,在矩形ABCD中,AB=3,对角线AC与BD相交于点O,
AE⊥BD,垂足为E,若BE=EO,则AD的长是( )
A.3 B. C. D.
8.如图,在矩形ABCD中,∠BDC的平分线交AB的延长线于点E,若AD=3,AE=9,则AB的长为( )
A.3.5 B.4 C.4.5 D.5
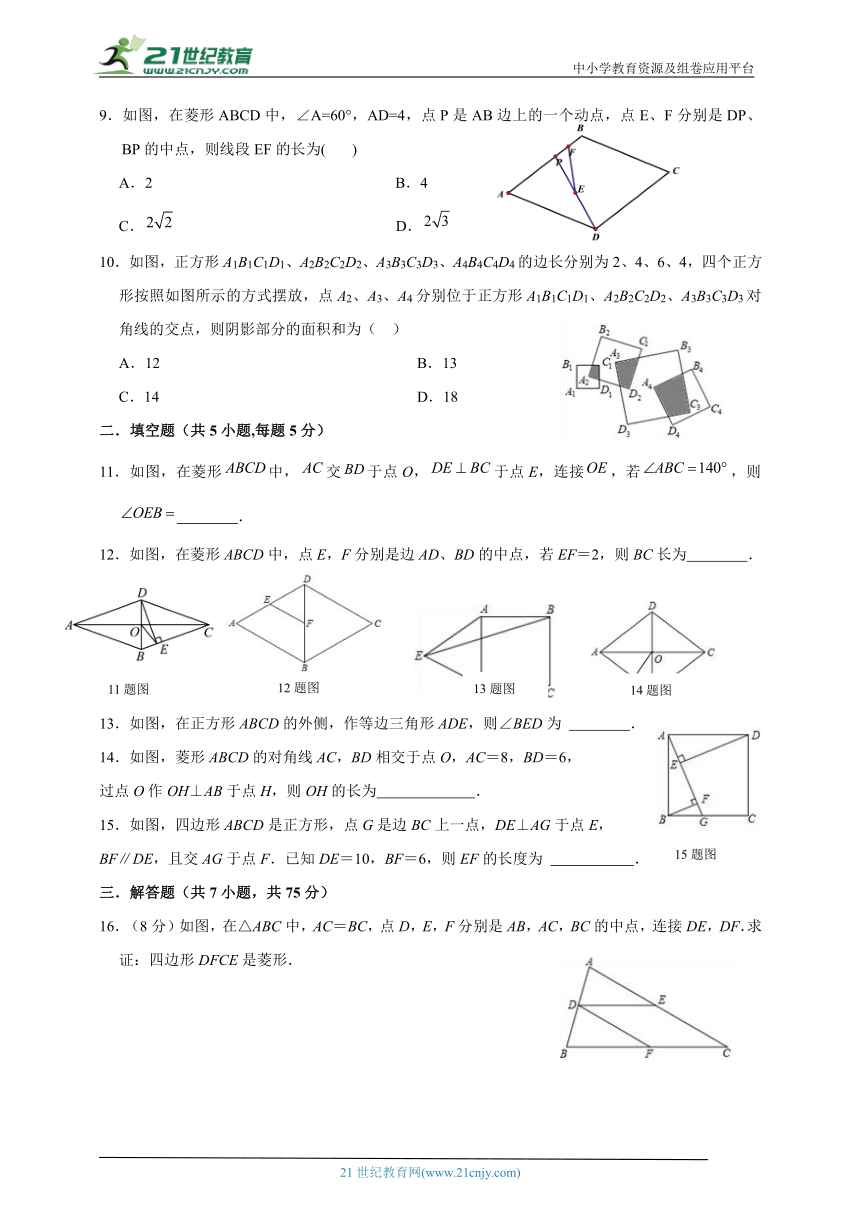
9.如图,在菱形ABCD中,∠A=60°,AD=4,点P是AB边上的一个动点,点E、F分别是DP、BP的中点,则线段EF的长为( )
A.2 B.4
C. D.
10.如图,正方形A1B1C1D1、A2B2C2D2、A3B3C3D3、A4B4C4D4的边长分别为2、4、6、4,四个正方形按照如图所示的方式摆放,点A2、A3、A4分别位于正方形A1B1C1D1、A2B2C2D2、A3B3C3D3对角线的交点,则阴影部分的面积和为( )
A.12 B.13
C.14 D.18
二.填空题(共5小题,每题5分)
11.如图,在菱形中,交于点O,于点E,连接,若,则 .
12.如图,在菱形ABCD中,点E,F分别是边AD、BD的中点,若EF=2,则BC长为 .
(
13题图
) (
12题图
)
(
14题图
) (
11题图
)
13.如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED为 .
14.如图,菱形ABCD的对角线AC,BD相交于点O,AC=8,BD=6,
过点O作OH⊥AB于点H,则OH的长为 .
(
15题图
)15.如图,四边形ABCD是正方形,点G是边BC上一点,DE⊥AG于点E,
BF∥DE,且交AG于点F.已知DE=10,BF=6,则EF的长度为 .
三.解答题(共7小题,共75分)
16.(8分)如图,在△ABC中,AC=BC,点D,E,F分别是AB,AC,BC的中点,连接DE,DF.求证:四边形DFCE是菱形.
17.(8分)如图,在矩形ABCD中,对角线AC,BD相交于点O,点E、F分别是AO,AD的中点,连接EF,AB=4cm,BC=6cm,求EF的长.
18.(8分)如图,在 ABCD中,E为CD边的中点,连接BE并延长,交AD的延长线于点F,延长ED至点G,使DG=DE,分别连接AE、AG、FG.
(1)求证:△BCE≌△FDE;
(2)当BF平分∠ABC时,四边形AEFG是什么特殊四边形?
19.(12分)23.如图,在正方形中,为上一点,连接,的垂直平分线交于点,交于点,垂足为,点在上,且.
(1)求证:;
(2)若,,求的长.
20.(12分)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,BD=2,求OE的长.
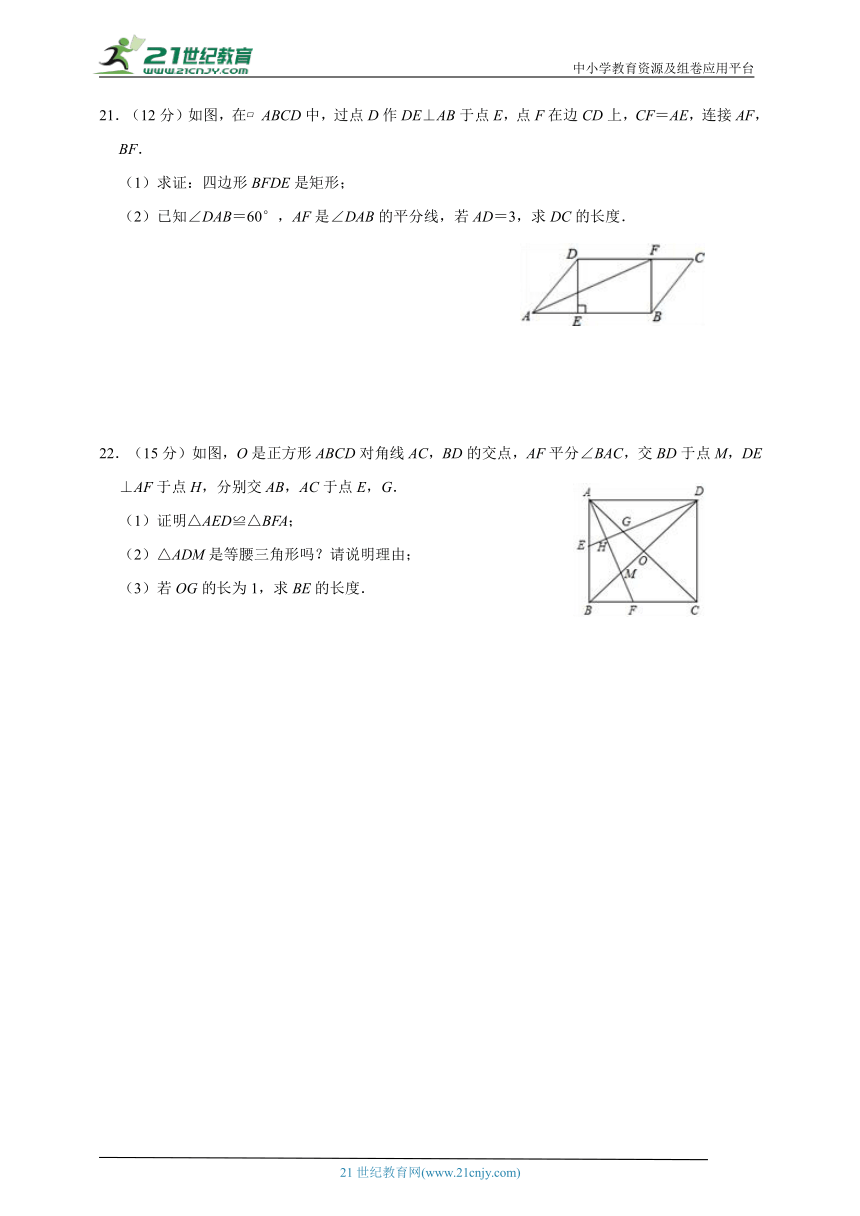
21.(12分)如图,在 ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)已知∠DAB=60°,AF是∠DAB的平分线,若AD=3,求DC的长度.
22.(15分)如图,O是正方形ABCD对角线AC,BD的交点,AF平分∠BAC,交BD于点M,DE⊥AF于点H,分别交AB,AC于点E,G.
(1)证明△AED≌△BFA;
(2)△ADM是等腰三角形吗?请说明理由;
(3)若OG的长为1,求BE的长度.
第六章 特殊平行四边形
一、选择题
1.D 2.D 3.B 4.A 5.B
6.B 7.B 8.B 9.D 10.C
二、填空题
11. 12.4 13.45° 14.12/5 15.4
三、解答题
16. 证明:∵点D,E,F分别是AB,AC,BC的中点,
∴DE∥CF,DE=1/2BC,DF∥CE,
DF=1/2AC,
∴四边形DECF是平行四边形,
∵AC=BC,
∴DE=DF,
∴四边形DFCE是菱形;
17.解:∵四边形ABCD是矩形,
∴∠ABC=90°,BD=AC,BO=OD,
∵AB=4cm,BC=6cm,
∴BD=AC=
AB2+BC2= 42+62=2 13(cm),
∴OD=1/2BD= 13(cm),
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,
∴EF=1/2OD= 13/2(cm)
18. (1)解:∵四边形ABCD是平行四边形,
∴ADBC,
∴∠DFE=∠CBE,
∵E为CD边的中点,
∴DE=CE,
在△BCE和△FDE中,
,
∴△BCE≌△FDE(AAS);
(2)解:四边形AEFG是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AD=BC,ADBC,
∴∠AFB=∠FBC,
由(1)得:△BCE≌△FDE,
∴BC=FD,BE=FE,
∴FD=AD,
∵GD=DE,
∴四边形AEFG是平行四边形,
∵BF平分∠ABC,
∴∠FBC=∠ABF,
∴∠AFB=∠ABF,
∴AF=AB,
∵BE=FE,
∴AE⊥FE,
∴∠AEF=90°,
∴平行四边形AEFG是矩形.
19. (1)在正方形ABCD中,有AD=DC=CB=AB,∠A=∠D=∠C=90°,,
,
∵,∠A=∠D=90°,,
∴四边形ADFM是矩形,
∴AD=MF,∠AMF=90°=∠MFD,
∴∠BMF=90°=∠NFM,即∠BMO+∠OMF=90°,AB=AD=MF,
∵MN是BE的垂直平分线,
∴MN⊥BE,
∴∠BOM=90°=∠BMO+∠MBO,
∴∠MBO=∠OMF,
∵,
∴△ABE≌△FMN;
(2)连接ME,如图,
∵AB=8,AE=6,
∴在Rt△ABE中,,
∴根据(1)中全等的结论可知MN=BE=10,
∵MN是BE的垂直平分线,
∴BO=OE==5,BM=ME,
∴AM=AB-BM=8-ME,
∴在Rt△AME中,,
∴,解得:,
∴,
∴在Rt△BMO中,,
∴,
∴ON=MN-MO=.
即NO的长为:.
20.(1)证明:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=1/2BD=1,
在Rt△AOB中,AB= 5,OB=1,
∴OA= AB2 OB2=2,
∴OE=OA=2.
21. 证明(1)∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB,
∵CF=AE,
∴DF=BE且DC∥AB,
∴四边形DFBE是平行四边形,
又∵DE⊥AB,
∴四边形DFBE是矩形;
(2)方法一:
∵∠DAB=60°,AD=3,DE⊥AB,
∴AE=32,DE= 3AE=3 3/2,
∵四边形DFBE是矩形,
∴BF=DE=3 3/2,
∵AF平分∠DAB,
∴∠FAB=12∠DAB=30°,且BF⊥AB,
∴DC=AB= 3BF=9/2.
方法二:
∵∠DAB=60°,AD=3,DE⊥AB,
∴AE=3/2,
∵AB∥DC,
∴∠AFD=∠BAF,
∵AF平分∠DAB,
∴∠DAF=∠BAF,
∴∠AFD=∠DAF,
∴DA=DF=3,
又DF=BE=3,
∴AB=AE+BE=9/2.
22. 解:(1)∵四边形ABCD为正方形,
∴∠DAE=∠ABF=90°,AD=AB,
∵DE⊥AF,
∴∠DAH+∠ADE=90°,
∵∠DAH+∠BAF=90°,
∴∠ADE=∠BAF,
在△AED和△BFA中,
∠ADE=∠BAF
AD=BA
∠DAE=∠ABF,
∴△AED≌△BFA(ASA).
(2)△ADM是等腰三角形,理由如下:
∵∠BAC=45°,AF平分∠BAC,
∴∠BAF=∠CAF=12∠BAC=22.5°,
∴∠DAM=∠DAC+∠CAF=67.5°,
∴∠DMA=180° ∠DAM ∠ADM=180° 67.5° 45°=67.5°,
∴∠DAM=∠DMA,
∴△ADM是等腰三角形.
(3)∵∠ADE=∠BAF=22.5°,
∴∠CDG=∠ADC ∠ADE=67.5°,
∴∠DGC=180° ∠GCD ∠CDG=67.5°,
∴CG=CB,
∵AE∥CD,
∴∠AEG=∠CDG=67.5°,
∴AE=AG,
作FK⊥AC于点K,设AG=AE=x,
∵AO=AG+OG=x+1,
∴AB=BC= 2AO= 2(x+1),
AC=2AO=2(x+1),
∵△AED≌△BFA,
∴BF=AE=x,
∵AF平分∠BAC,
∴FK=BF=x,
∵S△ABF=1/2AB BF,S△ACF=1/2AC FK,
∴S△ABFS△ACF=(1/2AB BF)/(1/2AC FK)=AB/AC,
又∵S△ABF/S△ACF=BF/FC,
∴ABAC=BFFC=BFBC BF,即
2(x+1)/2(x+1)=x/[ 2(x+1) x],
解得x= 2,
∴BE=AB AE= 2(x+1) x=2.
解法二:BF=x之后,可以直接AB=
2(x+1),BC=x+ 2x,
由AB=BC,可以直接解出x.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
八年级数学(下)第六章 特殊平行四边形检测题
一、选择题(共10个小题,每题5分)
1.关于四边形,下列说法正确的是( )
A.对角线相等的是矩形 B.对角线互相垂直的是菱形
C.对角线互相垂直且相等的是正方形 D.对角线互相平分的是平行四边形
2.在四边形ABCD中,两对角线交于点O,若OA=OB=OC=OD,则这个四边形( )
A.可能不是平行四边形 B.一定是菱形
C.一定是正方形 D.一定是矩形
3.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的( )
A. B. C. D.
4.如图,点E在正方形ABCD的对角线AC上,若AE=AB,则∠EBC的度数为( )
A.22.5° B.30° C.45° D.67.5°
5.如图,在平面直角坐标系中,菱形ABCD的顶点A在y轴上,顶点B,C的坐标分别为(﹣6,0),(4,0),则点D的坐标是( )
A.(6,8) B.(10,8) C.(10,6) D.(4,6)
(
6题图
) (
3题图
)
(
5题图
) (
4题图
)
6.如图.在正方形中,点在对角线上,,,,分别为垂足,连接,,则下列命题:①若,则:②若正方形边长为4,则的最小值为2:③若,则,其中正确的命题是( )
A.①② B.①③ C.②③ D.①②③
如图,在矩形ABCD中,AB=3,对角线AC与BD相交于点O,
AE⊥BD,垂足为E,若BE=EO,则AD的长是( )
A.3 B. C. D.
8.如图,在矩形ABCD中,∠BDC的平分线交AB的延长线于点E,若AD=3,AE=9,则AB的长为( )
A.3.5 B.4 C.4.5 D.5
9.如图,在菱形ABCD中,∠A=60°,AD=4,点P是AB边上的一个动点,点E、F分别是DP、BP的中点,则线段EF的长为( )
A.2 B.4
C. D.
10.如图,正方形A1B1C1D1、A2B2C2D2、A3B3C3D3、A4B4C4D4的边长分别为2、4、6、4,四个正方形按照如图所示的方式摆放,点A2、A3、A4分别位于正方形A1B1C1D1、A2B2C2D2、A3B3C3D3对角线的交点,则阴影部分的面积和为( )
A.12 B.13
C.14 D.18
二.填空题(共5小题,每题5分)
11.如图,在菱形中,交于点O,于点E,连接,若,则 .
12.如图,在菱形ABCD中,点E,F分别是边AD、BD的中点,若EF=2,则BC长为 .
(
13题图
) (
12题图
)
(
14题图
) (
11题图
)
13.如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED为 .
14.如图,菱形ABCD的对角线AC,BD相交于点O,AC=8,BD=6,
过点O作OH⊥AB于点H,则OH的长为 .
(
15题图
)15.如图,四边形ABCD是正方形,点G是边BC上一点,DE⊥AG于点E,
BF∥DE,且交AG于点F.已知DE=10,BF=6,则EF的长度为 .
三.解答题(共7小题,共75分)
16.(8分)如图,在△ABC中,AC=BC,点D,E,F分别是AB,AC,BC的中点,连接DE,DF.求证:四边形DFCE是菱形.
17.(8分)如图,在矩形ABCD中,对角线AC,BD相交于点O,点E、F分别是AO,AD的中点,连接EF,AB=4cm,BC=6cm,求EF的长.
18.(8分)如图,在 ABCD中,E为CD边的中点,连接BE并延长,交AD的延长线于点F,延长ED至点G,使DG=DE,分别连接AE、AG、FG.
(1)求证:△BCE≌△FDE;
(2)当BF平分∠ABC时,四边形AEFG是什么特殊四边形?
19.(12分)23.如图,在正方形中,为上一点,连接,的垂直平分线交于点,交于点,垂足为,点在上,且.
(1)求证:;
(2)若,,求的长.
20.(12分)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,BD=2,求OE的长.
21.(12分)如图,在 ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)已知∠DAB=60°,AF是∠DAB的平分线,若AD=3,求DC的长度.
22.(15分)如图,O是正方形ABCD对角线AC,BD的交点,AF平分∠BAC,交BD于点M,DE⊥AF于点H,分别交AB,AC于点E,G.
(1)证明△AED≌△BFA;
(2)△ADM是等腰三角形吗?请说明理由;
(3)若OG的长为1,求BE的长度.
第六章 特殊平行四边形
一、选择题
1.D 2.D 3.B 4.A 5.B
6.B 7.B 8.B 9.D 10.C
二、填空题
11. 12.4 13.45° 14.12/5 15.4
三、解答题
16. 证明:∵点D,E,F分别是AB,AC,BC的中点,
∴DE∥CF,DE=1/2BC,DF∥CE,
DF=1/2AC,
∴四边形DECF是平行四边形,
∵AC=BC,
∴DE=DF,
∴四边形DFCE是菱形;
17.解:∵四边形ABCD是矩形,
∴∠ABC=90°,BD=AC,BO=OD,
∵AB=4cm,BC=6cm,
∴BD=AC=
AB2+BC2= 42+62=2 13(cm),
∴OD=1/2BD= 13(cm),
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,
∴EF=1/2OD= 13/2(cm)
18. (1)解:∵四边形ABCD是平行四边形,
∴ADBC,
∴∠DFE=∠CBE,
∵E为CD边的中点,
∴DE=CE,
在△BCE和△FDE中,
,
∴△BCE≌△FDE(AAS);
(2)解:四边形AEFG是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AD=BC,ADBC,
∴∠AFB=∠FBC,
由(1)得:△BCE≌△FDE,
∴BC=FD,BE=FE,
∴FD=AD,
∵GD=DE,
∴四边形AEFG是平行四边形,
∵BF平分∠ABC,
∴∠FBC=∠ABF,
∴∠AFB=∠ABF,
∴AF=AB,
∵BE=FE,
∴AE⊥FE,
∴∠AEF=90°,
∴平行四边形AEFG是矩形.
19. (1)在正方形ABCD中,有AD=DC=CB=AB,∠A=∠D=∠C=90°,,
,
∵,∠A=∠D=90°,,
∴四边形ADFM是矩形,
∴AD=MF,∠AMF=90°=∠MFD,
∴∠BMF=90°=∠NFM,即∠BMO+∠OMF=90°,AB=AD=MF,
∵MN是BE的垂直平分线,
∴MN⊥BE,
∴∠BOM=90°=∠BMO+∠MBO,
∴∠MBO=∠OMF,
∵,
∴△ABE≌△FMN;
(2)连接ME,如图,
∵AB=8,AE=6,
∴在Rt△ABE中,,
∴根据(1)中全等的结论可知MN=BE=10,
∵MN是BE的垂直平分线,
∴BO=OE==5,BM=ME,
∴AM=AB-BM=8-ME,
∴在Rt△AME中,,
∴,解得:,
∴,
∴在Rt△BMO中,,
∴,
∴ON=MN-MO=.
即NO的长为:.
20.(1)证明:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=1/2BD=1,
在Rt△AOB中,AB= 5,OB=1,
∴OA= AB2 OB2=2,
∴OE=OA=2.
21. 证明(1)∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB,
∵CF=AE,
∴DF=BE且DC∥AB,
∴四边形DFBE是平行四边形,
又∵DE⊥AB,
∴四边形DFBE是矩形;
(2)方法一:
∵∠DAB=60°,AD=3,DE⊥AB,
∴AE=32,DE= 3AE=3 3/2,
∵四边形DFBE是矩形,
∴BF=DE=3 3/2,
∵AF平分∠DAB,
∴∠FAB=12∠DAB=30°,且BF⊥AB,
∴DC=AB= 3BF=9/2.
方法二:
∵∠DAB=60°,AD=3,DE⊥AB,
∴AE=3/2,
∵AB∥DC,
∴∠AFD=∠BAF,
∵AF平分∠DAB,
∴∠DAF=∠BAF,
∴∠AFD=∠DAF,
∴DA=DF=3,
又DF=BE=3,
∴AB=AE+BE=9/2.
22. 解:(1)∵四边形ABCD为正方形,
∴∠DAE=∠ABF=90°,AD=AB,
∵DE⊥AF,
∴∠DAH+∠ADE=90°,
∵∠DAH+∠BAF=90°,
∴∠ADE=∠BAF,
在△AED和△BFA中,
∠ADE=∠BAF
AD=BA
∠DAE=∠ABF,
∴△AED≌△BFA(ASA).
(2)△ADM是等腰三角形,理由如下:
∵∠BAC=45°,AF平分∠BAC,
∴∠BAF=∠CAF=12∠BAC=22.5°,
∴∠DAM=∠DAC+∠CAF=67.5°,
∴∠DMA=180° ∠DAM ∠ADM=180° 67.5° 45°=67.5°,
∴∠DAM=∠DMA,
∴△ADM是等腰三角形.
(3)∵∠ADE=∠BAF=22.5°,
∴∠CDG=∠ADC ∠ADE=67.5°,
∴∠DGC=180° ∠GCD ∠CDG=67.5°,
∴CG=CB,
∵AE∥CD,
∴∠AEG=∠CDG=67.5°,
∴AE=AG,
作FK⊥AC于点K,设AG=AE=x,
∵AO=AG+OG=x+1,
∴AB=BC= 2AO= 2(x+1),
AC=2AO=2(x+1),
∵△AED≌△BFA,
∴BF=AE=x,
∵AF平分∠BAC,
∴FK=BF=x,
∵S△ABF=1/2AB BF,S△ACF=1/2AC FK,
∴S△ABFS△ACF=(1/2AB BF)/(1/2AC FK)=AB/AC,
又∵S△ABF/S△ACF=BF/FC,
∴ABAC=BFFC=BFBC BF,即
2(x+1)/2(x+1)=x/[ 2(x+1) x],
解得x= 2,
∴BE=AB AE= 2(x+1) x=2.
解法二:BF=x之后,可以直接AB=
2(x+1),BC=x+ 2x,
由AB=BC,可以直接解出x.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
