第九章 图形的相似检测题(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
八年级数学(下)第九章 图形的相似检测题
一.选择题(共12小题,每题4分)
1.已知===,则=( )
A. B. C. D.
2.将矩形OABC如图放置,O为原点.若点A(﹣1,2),点B的纵坐标是 ,则点C的坐标是( )
A. (4,2) B. (2,4) C. ( ,3) D. (3, )
2题图 3题图 4题图 5题图
3.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC
C.= D.=
4.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( ) A. B. C. D.
5.如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( ) A. B. C. D.
6. 如图,在 ABCD中,AC与BD相交于点O,E为OD的中点,连结AE并延长交DC于点F,则S△DEF∶S△AOB的值为( )
A. B. C. D.
7.如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )
A.3.25m B.4.25m C.4.45m D.4.75m
8.如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=( )
A. B. C. D.
9.如图,已知正方形ABCD的边长为1,M是AB的中点,则图中阴影部分的面积是( )
B. C. D.
7题图 8题图 9题图 10题图
10.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
11.在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,
使△ADE与△ABC相似,则AE的长为( )
A. B. C.3或 D. 或
12.如图,正方形 的对角线 , 相交于点 , , 为 上一点, ,连接 ,过点 作 于点 ,与 交于点 ,则 的长为( ).
A. B.
C. D.
二.填空题(共6小题,每题4分)
13.如果,那么k
14. 点是线段的黄金分割点,且,则的长为
15.如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为
16.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,﹣1),则点B的坐标是________.
15题图 16题图 17题图
17.将一副三角板按图叠放,则△AOB与△DOC的面积之比等于 .
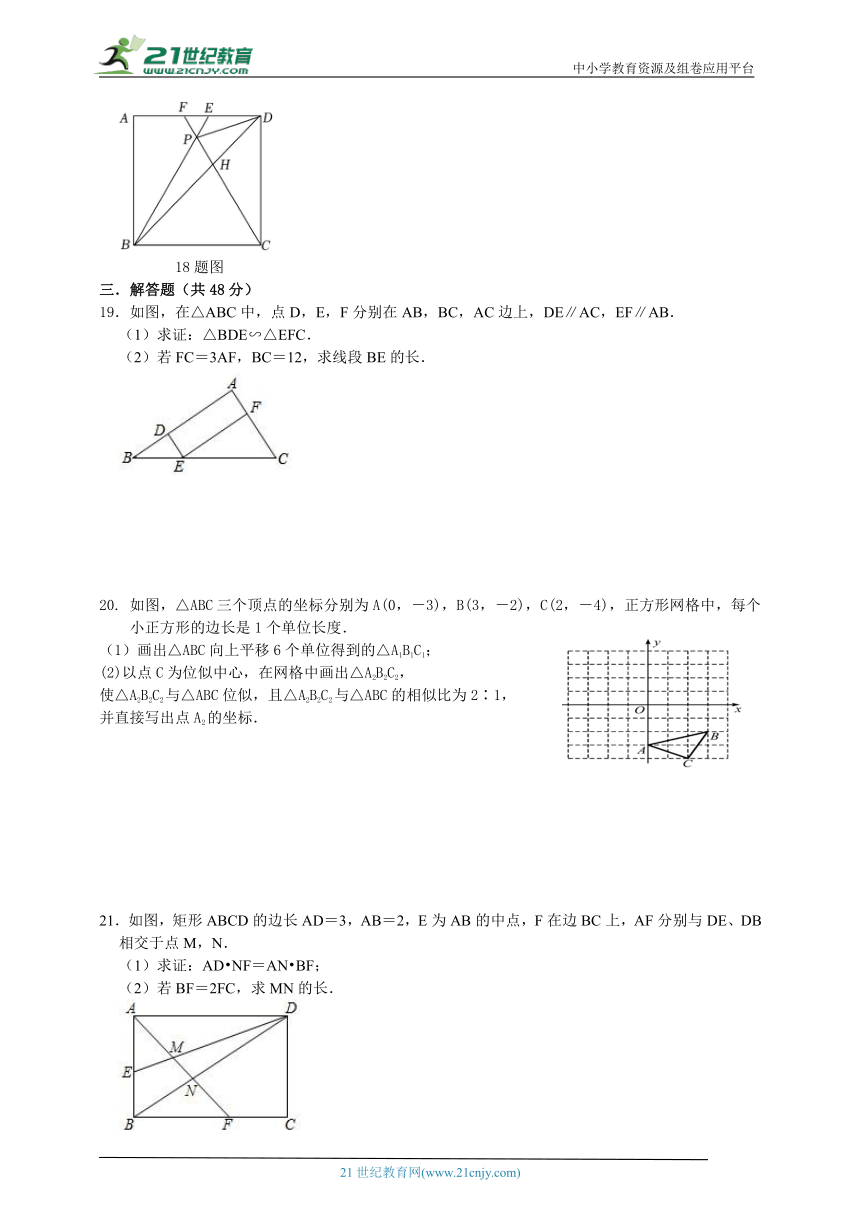
18.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:①BE=2AE;②△DFP∽△BPH;③PD=DH;④DP2=PH PB;其中正确的是 .
18题图
三.解答题(共48分)
19.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)若FC=3AF,BC=12,求线段BE的长.
如图,△ABC三个顶点的坐标分别为A(0,-3),B(3,-2),C(2,-4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,
使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的相似比为2∶1,
并直接写出点A2的坐标.
21.如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,AF分别与DE、DB相交于点M,N.
(1)求证:AD NF=AN BF;
(2)若BF=2FC,求MN的长.
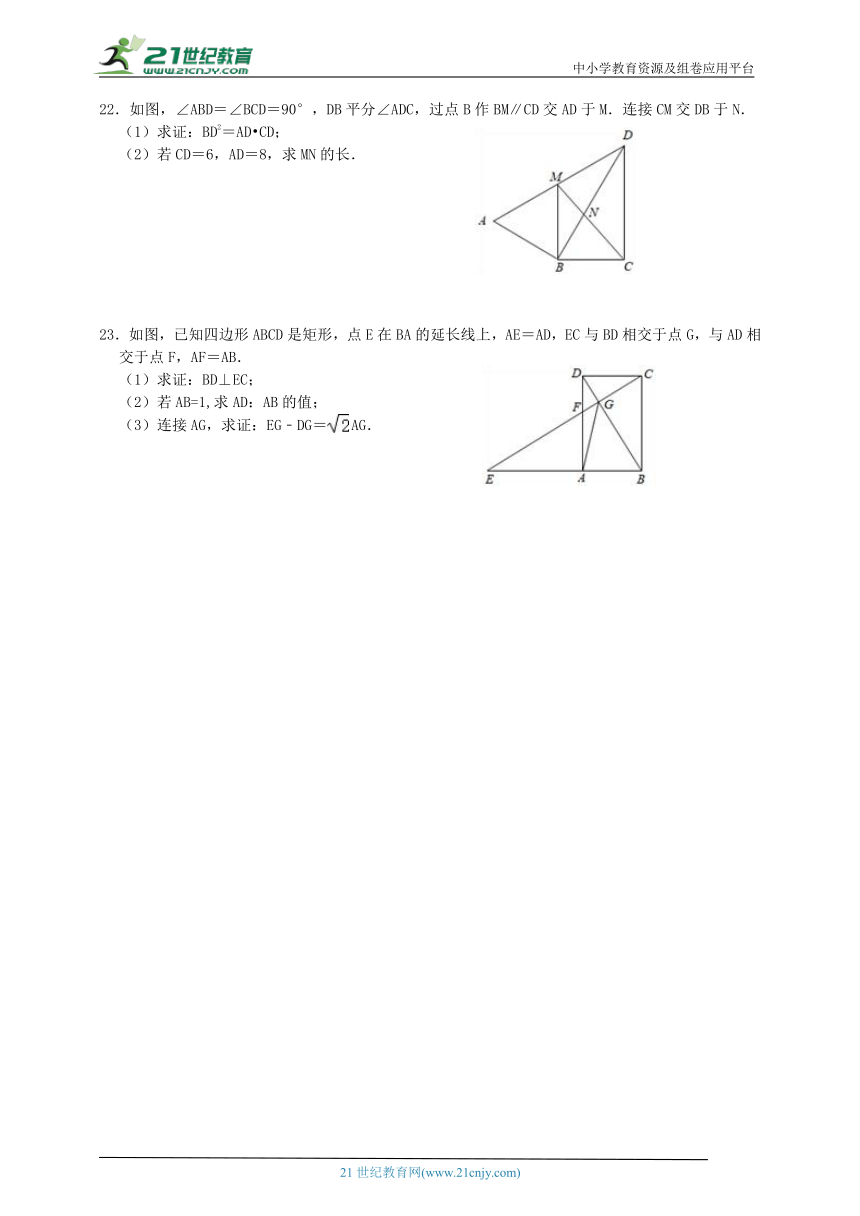
22.如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于M.连接CM交DB于N.
(1)求证:BD2=AD CD;
(2)若CD=6,AD=8,求MN的长.
23.如图,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD,EC与BD相交于点G,与AD相交于点F,AF=AB.
(1)求证:BD⊥EC;
(2)若AB=1,求AD:AB的值;
(3)连接AG,求证:EG﹣DG=AG.
第九章 图形的相似
一、选择题
1.C 2.D 3.D 4.C 5.D 6.C
7.C 8.B 9.D 10.A 11.D 12.A
二、填空题(每小题3分,共18分)
13.14.或 15.7 16.(﹣3, ). 17.1:3
三、解答题(本大题共7个小题,满分66分,解答题应写出必要的文字说明或推演步骤)
19.( 1)证明:∵DE∥AC,
∴∠BED=∠C,
又∵EF∥AB,
∴∠B=∠FEC,
∴△BDE∽△EFC;
(2)解:∵EF∥AB,
∴=,,
∵BC=12,
∴,
∴BE=3.
20. A2(-2,-2)
21.(1)证明:∵四边形ABCD为矩形,
∴AD∥BC,
∴△ADN∽△FBN,
∴AD:BF=AN:FN,
∴AD NF=AN BF;
(2)解:DE和CB的延长线交于H,如图,
∵BF=2FC,BC=3,
∴BF=2,
在Rt△ABF中,AF==2,
∵AD∥BH,
∴=,
而E为AB的中点,即AE=BE,
∴BH=AD=3,
∵AD∥FH,
∴==,
∴AM=AF=×2=,
∵AD NF=AN BF,
∴==,
∴AN=AF=×2=,
∴MN=AN﹣AM=﹣=.
22.证明:(1)∵DB平分,
∴,
∵
∴∽ΔBCD
BD:CD=AD:BD
BD=AD.CD
(2)MN=
23.解:(1)∵四边形ABCD是矩形,点E在BA的延长线上,
∴∠EAF=∠DAB=90°,
又∵AE=AD,AF=AB,
∴△AEF≌△ADB(SAS),
∴∠AEF=∠ADB,
∴∠GEB+∠GBE=∠ADB+∠ABD=90°,
即∠EGB=90°,
故BD⊥EC,
(2)∵四边形ABCD是矩形,
∴AE∥CD,
∴∠AEF=∠DCF,∠EAF=∠CDF,
∴△AEF∽△DCF,
∴AE/DC=AF/DF,
即AE DF=AF DC,
设AE=AD=a(a>0),则有a (a﹣1)=1,化简得a2﹣a﹣1=0,
解得a=(1+√5)/2或(1-√5)/2(舍去),
∴AE=(1+√5)/2.
(3)如图,在线段EG上取点P,使得EP=DG,
在△AEP与△ADG中,AE=AD,∠AEP=∠ADG,EP=DG,
∴△AEP≌△ADG(SAS),
∴AP=AG,∠EAP=∠DAG,
∴∠PAG=∠PAD+∠DAG=∠PAD+∠EAP=∠DAE=90°,
∴△PAG为等腰直角三角形,
∴EG﹣DG=EG﹣EP=PG=√2AG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
八年级数学(下)第九章 图形的相似检测题
一.选择题(共12小题,每题4分)
1.已知===,则=( )
A. B. C. D.
2.将矩形OABC如图放置,O为原点.若点A(﹣1,2),点B的纵坐标是 ,则点C的坐标是( )
A. (4,2) B. (2,4) C. ( ,3) D. (3, )
2题图 3题图 4题图 5题图
3.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC
C.= D.=
4.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( ) A. B. C. D.
5.如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( ) A. B. C. D.
6. 如图,在 ABCD中,AC与BD相交于点O,E为OD的中点,连结AE并延长交DC于点F,则S△DEF∶S△AOB的值为( )
A. B. C. D.
7.如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )
A.3.25m B.4.25m C.4.45m D.4.75m
8.如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=( )
A. B. C. D.
9.如图,已知正方形ABCD的边长为1,M是AB的中点,则图中阴影部分的面积是( )
B. C. D.
7题图 8题图 9题图 10题图
10.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
11.在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,
使△ADE与△ABC相似,则AE的长为( )
A. B. C.3或 D. 或
12.如图,正方形 的对角线 , 相交于点 , , 为 上一点, ,连接 ,过点 作 于点 ,与 交于点 ,则 的长为( ).
A. B.
C. D.
二.填空题(共6小题,每题4分)
13.如果,那么k
14. 点是线段的黄金分割点,且,则的长为
15.如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为
16.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,﹣1),则点B的坐标是________.
15题图 16题图 17题图
17.将一副三角板按图叠放,则△AOB与△DOC的面积之比等于 .
18.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:①BE=2AE;②△DFP∽△BPH;③PD=DH;④DP2=PH PB;其中正确的是 .
18题图
三.解答题(共48分)
19.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)若FC=3AF,BC=12,求线段BE的长.
如图,△ABC三个顶点的坐标分别为A(0,-3),B(3,-2),C(2,-4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,
使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的相似比为2∶1,
并直接写出点A2的坐标.
21.如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,AF分别与DE、DB相交于点M,N.
(1)求证:AD NF=AN BF;
(2)若BF=2FC,求MN的长.
22.如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于M.连接CM交DB于N.
(1)求证:BD2=AD CD;
(2)若CD=6,AD=8,求MN的长.
23.如图,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD,EC与BD相交于点G,与AD相交于点F,AF=AB.
(1)求证:BD⊥EC;
(2)若AB=1,求AD:AB的值;
(3)连接AG,求证:EG﹣DG=AG.
第九章 图形的相似
一、选择题
1.C 2.D 3.D 4.C 5.D 6.C
7.C 8.B 9.D 10.A 11.D 12.A
二、填空题(每小题3分,共18分)
13.14.或 15.7 16.(﹣3, ). 17.1:3
三、解答题(本大题共7个小题,满分66分,解答题应写出必要的文字说明或推演步骤)
19.( 1)证明:∵DE∥AC,
∴∠BED=∠C,
又∵EF∥AB,
∴∠B=∠FEC,
∴△BDE∽△EFC;
(2)解:∵EF∥AB,
∴=,,
∵BC=12,
∴,
∴BE=3.
20. A2(-2,-2)
21.(1)证明:∵四边形ABCD为矩形,
∴AD∥BC,
∴△ADN∽△FBN,
∴AD:BF=AN:FN,
∴AD NF=AN BF;
(2)解:DE和CB的延长线交于H,如图,
∵BF=2FC,BC=3,
∴BF=2,
在Rt△ABF中,AF==2,
∵AD∥BH,
∴=,
而E为AB的中点,即AE=BE,
∴BH=AD=3,
∵AD∥FH,
∴==,
∴AM=AF=×2=,
∵AD NF=AN BF,
∴==,
∴AN=AF=×2=,
∴MN=AN﹣AM=﹣=.
22.证明:(1)∵DB平分,
∴,
∵
∴∽ΔBCD
BD:CD=AD:BD
BD=AD.CD
(2)MN=
23.解:(1)∵四边形ABCD是矩形,点E在BA的延长线上,
∴∠EAF=∠DAB=90°,
又∵AE=AD,AF=AB,
∴△AEF≌△ADB(SAS),
∴∠AEF=∠ADB,
∴∠GEB+∠GBE=∠ADB+∠ABD=90°,
即∠EGB=90°,
故BD⊥EC,
(2)∵四边形ABCD是矩形,
∴AE∥CD,
∴∠AEF=∠DCF,∠EAF=∠CDF,
∴△AEF∽△DCF,
∴AE/DC=AF/DF,
即AE DF=AF DC,
设AE=AD=a(a>0),则有a (a﹣1)=1,化简得a2﹣a﹣1=0,
解得a=(1+√5)/2或(1-√5)/2(舍去),
∴AE=(1+√5)/2.
(3)如图,在线段EG上取点P,使得EP=DG,
在△AEP与△ADG中,AE=AD,∠AEP=∠ADG,EP=DG,
∴△AEP≌△ADG(SAS),
∴AP=AG,∠EAP=∠DAG,
∴∠PAG=∠PAD+∠DAG=∠PAD+∠EAP=∠DAE=90°,
∴△PAG为等腰直角三角形,
∴EG﹣DG=EG﹣EP=PG=√2AG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
