8.6一元二次方程的应用(1)学案(含答案)
文档属性
| 名称 | 8.6一元二次方程的应用(1)学案(含答案) | 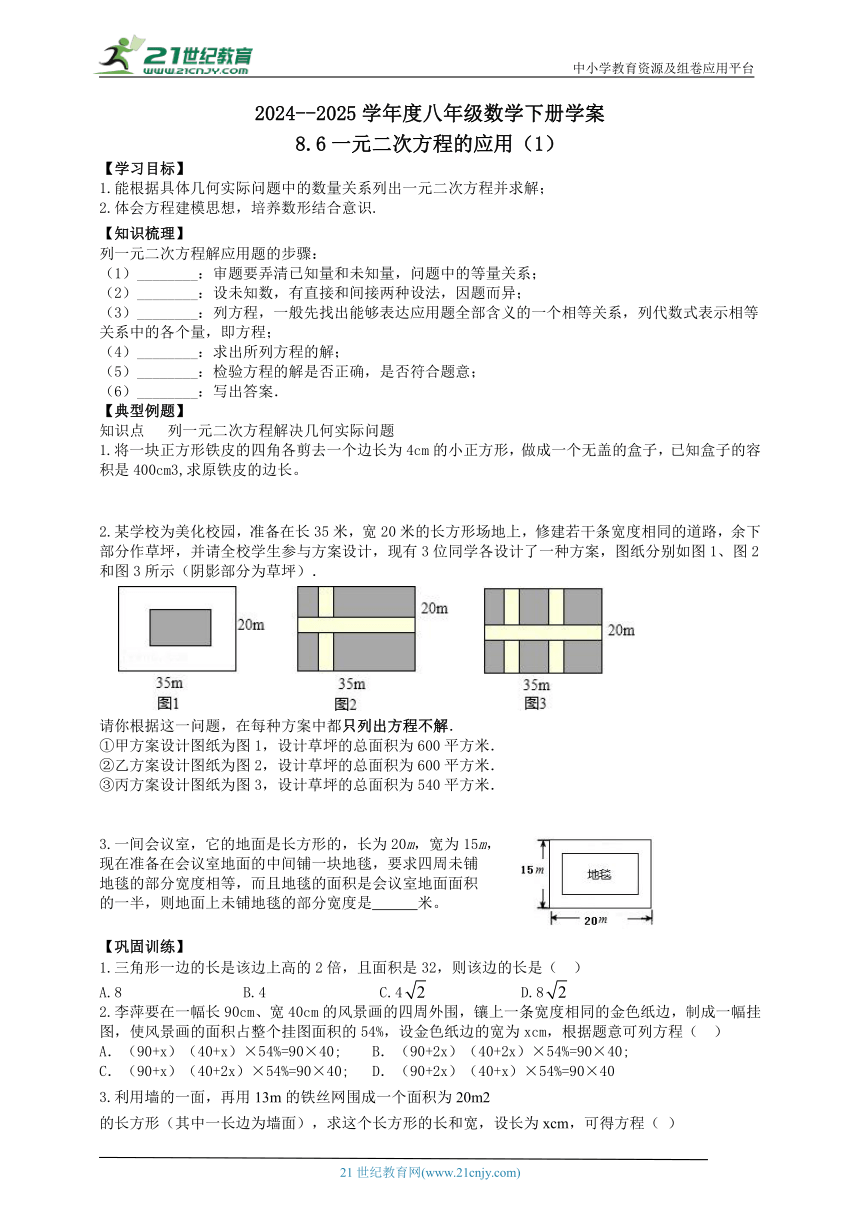 | |
| 格式 | doc | ||
| 文件大小 | 326.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-18 21:11:11 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024--2025学年度八年级数学下册学案
8.6一元二次方程的应用(1)
【学习目标】
1.能根据具体几何实际问题中的数量关系列出一元二次方程并求解;
2.体会方程建模思想,培养数形结合意识.
【知识梳理】
列一元二次方程解应用题的步骤:
(1)________:审题要弄清已知量和未知量,问题中的等量关系;
(2)________:设未知数,有直接和间接两种设法,因题而异;
(3)________:列方程,一般先找出能够表达应用题全部含义的一个相等关系,列代数式表示相等关系中的各个量,即方程;
(4)________:求出所列方程的解;
(5)________:检验方程的解是否正确,是否符合题意;
(6)________:写出答案.
【典型例题】
知识点 列一元二次方程解决几何实际问题
1.将一块正方形铁皮的四角各剪去一个边长为4cm的小正方形,做成一个无盖的盒子,已知盒子的容积是400cm3,求原铁皮的边长。
2.某学校为美化校园,准备在长35米,宽20米的长方形场地上,修建若干条宽度相同的道路,余下部分作草坪,并请全校学生参与方案设计,现有3位同学各设计了一种方案,图纸分别如图1、图2和图3所示(阴影部分为草坪).
请你根据这一问题,在每种方案中都只列出方程不解.
①甲方案设计图纸为图1,设计草坪的总面积为600平方米.
②乙方案设计图纸为图2,设计草坪的总面积为600平方米.
③丙方案设计图纸为图3,设计草坪的总面积为540平方米.
3.一间会议室,它的地面是长方形的,长为20m,宽为15m,
现在准备在会议室地面的中间铺一块地毯,要求四周未铺
地毯的部分宽度相等,而且地毯的面积是会议室地面面积
的一半,则地面上未铺地毯的部分宽度是 米。
【巩固训练】
1.三角形一边的长是该边上高的2倍,且面积是32,则该边的长是( )
A.8 B.4 C.4 D.8
2.李萍要在一幅长90cm、宽40cm的风景画的四周外围,镶上一条宽度相同的金色纸边,制成一幅挂图,使风景画的面积占整个挂图面积的54%,设金色纸边的宽为xcm,根据题意可列方程( )
A.(90+x)(40+x)×54%=90×40; B.(90+2x)(40+2x)×54%=90×40;
C.(90+x)(40+2x)×54%=90×40; D.(90+2x)(40+x)×54%=90×40
3.利用墙的一面,再用13m的铁丝网围成一个面积为20m2
的长方形(其中一长边为墙面),求这个长方形的长和宽,设长为xcm,可得方程( )
4..如图1,某广场一角的矩形花草区,其长为40m,宽为26m,其间有三条等宽的路,一条直路,两条曲路,路以外的地方全部种上花草,要使花草的面积为864m2,则路的宽度为 .
5.一条长12cm的铁丝围成一个斜边长是5cm的直角三角形,则这个直角三角形的两条直角边的长分别是( )
A. 1cm和6cm B. 2cm和5cm C. 3cm和4cm D.都是3.5cm
6.如图所示,某农户想建造一花圃,用来种植两种不同的花卉,以供应城镇市场需要,现用长为36m的篱笆,一面砌墙(墙的最大可使用长度为13m),围成中间隔有一道篱笆的长方形花圃.问花圃的宽AB为多少米时,围成的面积为96?
小明家要建养鸡场,鸡场一边靠墙另三遍用竹篱笆围成 如果竹篱笆总长45米 ,墙长15米.
(1) 可围成矩形的养鸡场面积面积最大是多少
(2)围成鸡场的面积可否恰好是100平方米
8.6 一元二次方程的应用(1)
【知识梳理】1.审 设 列 解 验 答
1.18 2.cm cm
【典型例题】
1.10cm 6cm 2. 5cm 24
3.解:设地面上未铺地毯的部分宽度是m,由题意,得
(20 2x)(15 2x)=×20×15,解得=15(不合题意,舍去),=2.5.
∴x=2.5. 答:地面上未铺地毯的部分宽度是2.5米。
【巩固训练】
D 2.B 3.B 4.2M 5.C
6.解:设花圃的宽AB为米,由题意,得 解得=4(不合题意,舍去),=8.答:花圃的宽AB为8米.
7.拓展延伸
周长相等的长方形,长和宽相等时面积最大,即为正方形时面积最大
所以边长为45÷3=15米
刚好另一边靠墙的长夜为15米
此时面积为15*15=225m
要想面积为100m ,设长方形的宽为x,长就为45-2x
x(45-2x)=100
45x-2x =100
2x -45x+100=0
此时Δ=b -4ac=1225>0
所以方程有实数根
即面积可以为100m
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024--2025学年度八年级数学下册学案
8.6一元二次方程的应用(1)
【学习目标】
1.能根据具体几何实际问题中的数量关系列出一元二次方程并求解;
2.体会方程建模思想,培养数形结合意识.
【知识梳理】
列一元二次方程解应用题的步骤:
(1)________:审题要弄清已知量和未知量,问题中的等量关系;
(2)________:设未知数,有直接和间接两种设法,因题而异;
(3)________:列方程,一般先找出能够表达应用题全部含义的一个相等关系,列代数式表示相等关系中的各个量,即方程;
(4)________:求出所列方程的解;
(5)________:检验方程的解是否正确,是否符合题意;
(6)________:写出答案.
【典型例题】
知识点 列一元二次方程解决几何实际问题
1.将一块正方形铁皮的四角各剪去一个边长为4cm的小正方形,做成一个无盖的盒子,已知盒子的容积是400cm3,求原铁皮的边长。
2.某学校为美化校园,准备在长35米,宽20米的长方形场地上,修建若干条宽度相同的道路,余下部分作草坪,并请全校学生参与方案设计,现有3位同学各设计了一种方案,图纸分别如图1、图2和图3所示(阴影部分为草坪).
请你根据这一问题,在每种方案中都只列出方程不解.
①甲方案设计图纸为图1,设计草坪的总面积为600平方米.
②乙方案设计图纸为图2,设计草坪的总面积为600平方米.
③丙方案设计图纸为图3,设计草坪的总面积为540平方米.
3.一间会议室,它的地面是长方形的,长为20m,宽为15m,
现在准备在会议室地面的中间铺一块地毯,要求四周未铺
地毯的部分宽度相等,而且地毯的面积是会议室地面面积
的一半,则地面上未铺地毯的部分宽度是 米。
【巩固训练】
1.三角形一边的长是该边上高的2倍,且面积是32,则该边的长是( )
A.8 B.4 C.4 D.8
2.李萍要在一幅长90cm、宽40cm的风景画的四周外围,镶上一条宽度相同的金色纸边,制成一幅挂图,使风景画的面积占整个挂图面积的54%,设金色纸边的宽为xcm,根据题意可列方程( )
A.(90+x)(40+x)×54%=90×40; B.(90+2x)(40+2x)×54%=90×40;
C.(90+x)(40+2x)×54%=90×40; D.(90+2x)(40+x)×54%=90×40
3.利用墙的一面,再用13m的铁丝网围成一个面积为20m2
的长方形(其中一长边为墙面),求这个长方形的长和宽,设长为xcm,可得方程( )
4..如图1,某广场一角的矩形花草区,其长为40m,宽为26m,其间有三条等宽的路,一条直路,两条曲路,路以外的地方全部种上花草,要使花草的面积为864m2,则路的宽度为 .
5.一条长12cm的铁丝围成一个斜边长是5cm的直角三角形,则这个直角三角形的两条直角边的长分别是( )
A. 1cm和6cm B. 2cm和5cm C. 3cm和4cm D.都是3.5cm
6.如图所示,某农户想建造一花圃,用来种植两种不同的花卉,以供应城镇市场需要,现用长为36m的篱笆,一面砌墙(墙的最大可使用长度为13m),围成中间隔有一道篱笆的长方形花圃.问花圃的宽AB为多少米时,围成的面积为96?
小明家要建养鸡场,鸡场一边靠墙另三遍用竹篱笆围成 如果竹篱笆总长45米 ,墙长15米.
(1) 可围成矩形的养鸡场面积面积最大是多少
(2)围成鸡场的面积可否恰好是100平方米
8.6 一元二次方程的应用(1)
【知识梳理】1.审 设 列 解 验 答
1.18 2.cm cm
【典型例题】
1.10cm 6cm 2. 5cm 24
3.解:设地面上未铺地毯的部分宽度是m,由题意,得
(20 2x)(15 2x)=×20×15,解得=15(不合题意,舍去),=2.5.
∴x=2.5. 答:地面上未铺地毯的部分宽度是2.5米。
【巩固训练】
D 2.B 3.B 4.2M 5.C
6.解:设花圃的宽AB为米,由题意,得 解得=4(不合题意,舍去),=8.答:花圃的宽AB为8米.
7.拓展延伸
周长相等的长方形,长和宽相等时面积最大,即为正方形时面积最大
所以边长为45÷3=15米
刚好另一边靠墙的长夜为15米
此时面积为15*15=225m
要想面积为100m ,设长方形的宽为x,长就为45-2x
x(45-2x)=100
45x-2x =100
2x -45x+100=0
此时Δ=b -4ac=1225>0
所以方程有实数根
即面积可以为100m
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
