9.8 相似三角形的性质(1)学案(含答案)
文档属性
| 名称 | 9.8 相似三角形的性质(1)学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 343.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-18 21:30:16 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024--2025学年度八年级数学下册第九章学案
9.8 相似三角形的性质(1)
【学习目标】
1.掌握相似三角形的性质定理及其证明方法;
2.能运用相似三角形性质定理解决问题;
3.通过全等三形与相似三角形的类比学习,感受学生从特殊到一般的认识规律.
【知识梳理】
相似三角形的对应角 、对应边 .
相似比: .
相似三角形 的比、 的比、 的比都等于相似比.
【典型例题】
知识点 相似三角形对应线段的比都等于相似比
1.若△ABC∽△DEF,相似比为3∶2,则对应高的比为( )
A.3∶2 B.3∶5 C.9∶4 D.4∶9
2.若△ABC∽△DEF,相似比为4∶3,则△ABC与△DEF对应的中线之比为( )
A.4∶3 B.3∶4 C.16∶9 D.9∶16
3.如图,在 ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的对应角平分线之比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶5
4.如图所示,某校宣传栏后面米处种了一排树,每隔米一棵,共种了棵,小勇站在距宣传栏中间位置的垂直距离米处,正好看到两端的树干,其余的棵均被挡住,那么宣传栏的长为________米.(不计宣传栏的厚度)
【巩固训练】
1.△ABC与△DEF的相似比为1:2,则△ABC与△DEF的周长比为 ( )
A. 1:2 B. 1:3 C. 1:4 D. 1:16
2.如果△ABC∽△A′B′C′,BC=3,B′C′=1.8,则△A′B′C′与△ABC的对应边上的对应高的相似比为( )
A.5∶3 B.3∶2 C.2∶3 D.3∶5
3.若的周长为,点D,E,F分别是三边的中点,则的周长为( )
A. B. C. D.
4. 一张等腰三角形纸片,底边长l5cm,底边上的高长22.5cm.
现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,已知剪得
的纸条中有一张是正方形,这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
5.若两个相似三角形的相似比是3∶5,则它们的对应高线的比是 ,对应中线的比是 ,对应角平分线的比是 .
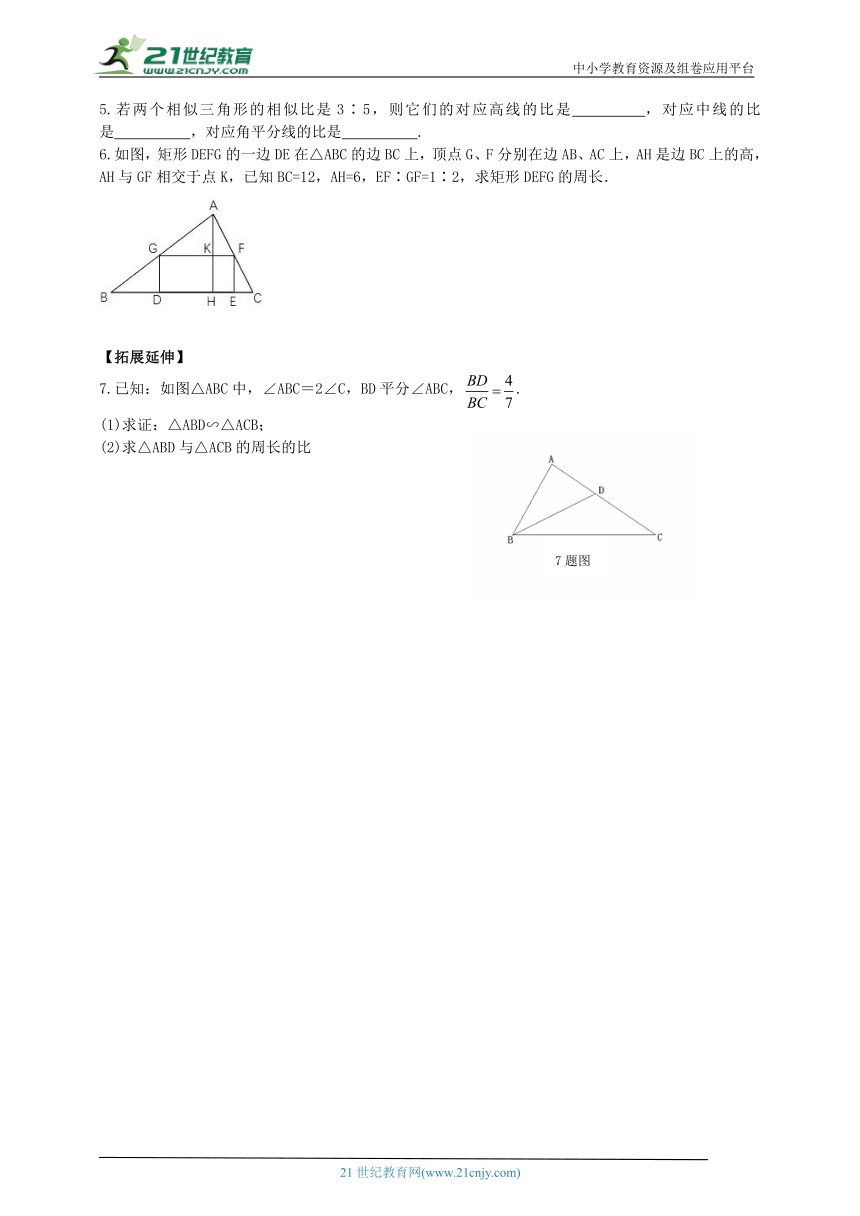
6.如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF∶GF=1∶2,求矩形DEFG的周长.
【拓展延伸】
7.已知:如图△ABC中,∠ABC=2∠C,BD平分∠ABC,.
(1)求证:△ABD∽△ACB;
(2)求△ABD与△ACB的周长的比
9.8 相似三角形的性质(1)
【典型例题】
1.A 2. A 3. 6
【巩固训练】
1.A 2.D 3.B 4.C
5.3:5;3:5;3:5
6.解:设EF=x,则GF=2x.
∵GF∥BC,AH⊥BC,
∴AK⊥GF.
∵GF∥BC,
∴△AGF∽△ABC,
∴ .
∵AH=6,BC=12,
解得x=3.
∴矩形DEFG的周长为18
【拓展延伸】
7.(1)证明:∵∠ABC=2∠C, BD平分∠B
∴∠ABD=∠ACB
∵∠ADB=∠ABC, ∠BAD=∠CAB
∴△ABD∽△ACB
(2)解:∵△ABD∽△ACB
∴k=
∴
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024--2025学年度八年级数学下册第九章学案
9.8 相似三角形的性质(1)
【学习目标】
1.掌握相似三角形的性质定理及其证明方法;
2.能运用相似三角形性质定理解决问题;
3.通过全等三形与相似三角形的类比学习,感受学生从特殊到一般的认识规律.
【知识梳理】
相似三角形的对应角 、对应边 .
相似比: .
相似三角形 的比、 的比、 的比都等于相似比.
【典型例题】
知识点 相似三角形对应线段的比都等于相似比
1.若△ABC∽△DEF,相似比为3∶2,则对应高的比为( )
A.3∶2 B.3∶5 C.9∶4 D.4∶9
2.若△ABC∽△DEF,相似比为4∶3,则△ABC与△DEF对应的中线之比为( )
A.4∶3 B.3∶4 C.16∶9 D.9∶16
3.如图,在 ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的对应角平分线之比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶5
4.如图所示,某校宣传栏后面米处种了一排树,每隔米一棵,共种了棵,小勇站在距宣传栏中间位置的垂直距离米处,正好看到两端的树干,其余的棵均被挡住,那么宣传栏的长为________米.(不计宣传栏的厚度)
【巩固训练】
1.△ABC与△DEF的相似比为1:2,则△ABC与△DEF的周长比为 ( )
A. 1:2 B. 1:3 C. 1:4 D. 1:16
2.如果△ABC∽△A′B′C′,BC=3,B′C′=1.8,则△A′B′C′与△ABC的对应边上的对应高的相似比为( )
A.5∶3 B.3∶2 C.2∶3 D.3∶5
3.若的周长为,点D,E,F分别是三边的中点,则的周长为( )
A. B. C. D.
4. 一张等腰三角形纸片,底边长l5cm,底边上的高长22.5cm.
现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,已知剪得
的纸条中有一张是正方形,这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
5.若两个相似三角形的相似比是3∶5,则它们的对应高线的比是 ,对应中线的比是 ,对应角平分线的比是 .
6.如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF∶GF=1∶2,求矩形DEFG的周长.
【拓展延伸】
7.已知:如图△ABC中,∠ABC=2∠C,BD平分∠ABC,.
(1)求证:△ABD∽△ACB;
(2)求△ABD与△ACB的周长的比
9.8 相似三角形的性质(1)
【典型例题】
1.A 2. A 3. 6
【巩固训练】
1.A 2.D 3.B 4.C
5.3:5;3:5;3:5
6.解:设EF=x,则GF=2x.
∵GF∥BC,AH⊥BC,
∴AK⊥GF.
∵GF∥BC,
∴△AGF∽△ABC,
∴ .
∵AH=6,BC=12,
解得x=3.
∴矩形DEFG的周长为18
【拓展延伸】
7.(1)证明:∵∠ABC=2∠C, BD平分∠B
∴∠ABD=∠ACB
∵∠ADB=∠ABC, ∠BAD=∠CAB
∴△ABD∽△ACB
(2)解:∵△ABD∽△ACB
∴k=
∴
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
