6.2矩形的性质与判断(3)学案(含答案)
文档属性
| 名称 | 6.2矩形的性质与判断(3)学案(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 377.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-18 22:09:24 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024-2025学年度八年级数学下册学案
6.2矩形的性质与判断(3)
【学习目标】
会灵活运用矩形的性质与判定定理进行有关的论证或计算.
【课前梳理】
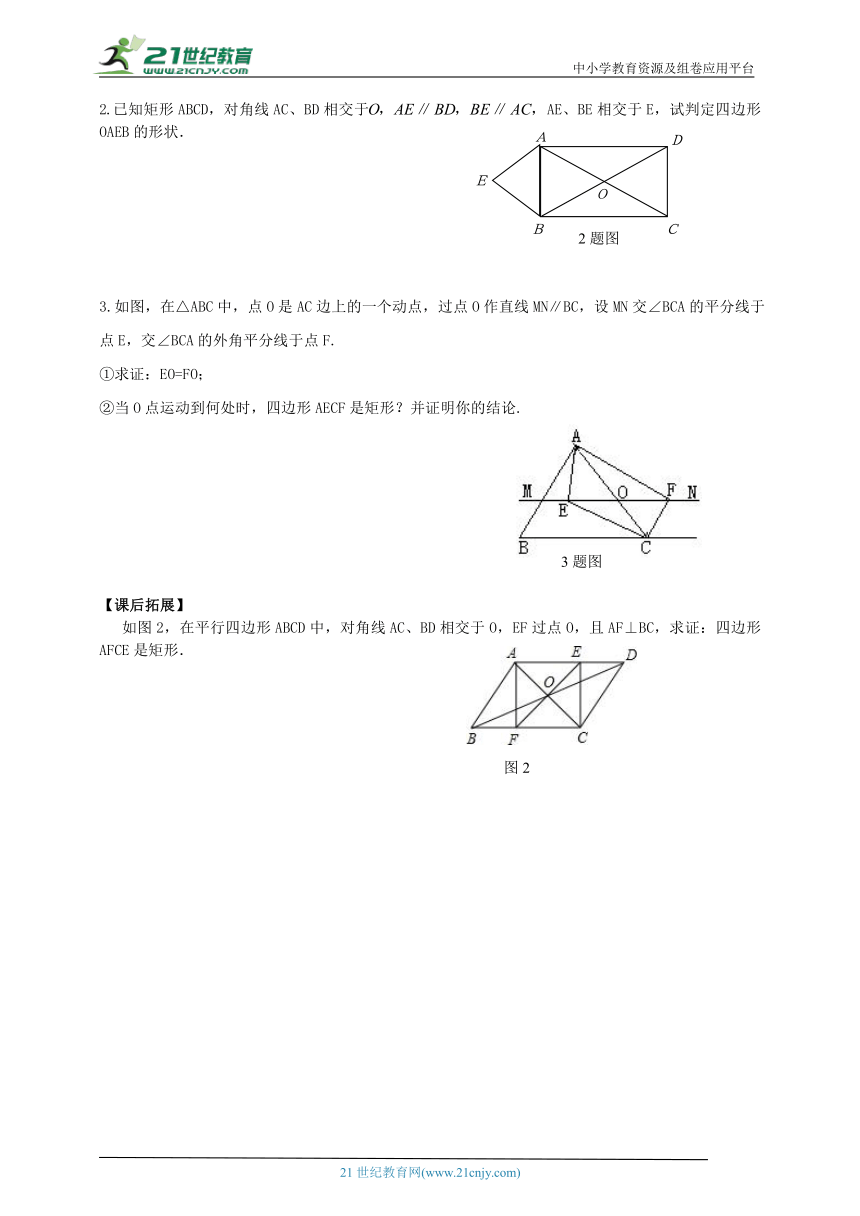
已知:如图,点E、F、D分别是各边的中点,且.求证:四边形是矩形.
【课堂练习】预习课本P18~19页内容,完成下列各题
1.如图,O是菱形对角线的交点,,,连接,设,,求的长.
(
1题图
)
2. 如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,DF⊥AC于点F. 求证:AE=DF.
(
2题图
)
【当堂达标】
1.下列各句判定矩形的说法是否正确?为什么?
(1)四个角都相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)对角线相等,且有一个角是直角的四边形是矩形;
(4)两组对边分别平行,且对角线相等的四边形是矩形.
(
A
B
C
D
O
E
2题图
)2.已知矩形ABCD,对角线AC、BD相交于 AE、BE相交于E,试判定四边形OAEB的形状.
3.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
①求证:EO=FO;
(
3题图
)②当O点运动到何处时,四边形AECF是矩形?并证明你的结论.
【课后拓展】
(
图
2
)如图2,在平行四边形ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC,求证:四边形AFCE是矩形.
6.2矩形的性质与判断(3)
【知识梳理】
1.有一个角是直角的平行四边形
2.对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
【巩固练习】
1.B 2.C 3.C 4.D
5. 解:(证明:四边形为菱形,
∴,
∴,
∵,,
,,
在和中,
,
,
,
∴四边形为平 四边形,
,
∴为矩形.
6(1)证明:∵四边形ABCD是平行四边形,
∴DA∥CB,
∴∠EAF=∠EBC,
∵点E是边AB的中点,
∴AE=BE,
在△AEF和△BEC中,
∠EAF=∠ECB
AE=BE
∠AEF=∠BEC,
∴△AEF≌△BEC(ASA),
∴EF=EC,
又∵AE=BE,
∴四边形AFBC是平行四边形;
(2)解:当∠AEC的度数为100度时,四边形AFBC是矩形,
理由:∵四边形AFBC是矩形,
∴AB=CF,
∴EC=EB,
∴∠ECB=∠EBC,
∵四边形ABCD是平行四边形,∠D=50°,
∴∠D=∠EBC=50°,
∴∠ECB=50°,
∴∠AEC=∠ECB+∠EBC=50°+50°=100°,
故答案为:100.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年度八年级数学下册学案
6.2矩形的性质与判断(3)
【学习目标】
会灵活运用矩形的性质与判定定理进行有关的论证或计算.
【课前梳理】
已知:如图,点E、F、D分别是各边的中点,且.求证:四边形是矩形.
【课堂练习】预习课本P18~19页内容,完成下列各题
1.如图,O是菱形对角线的交点,,,连接,设,,求的长.
(
1题图
)
2. 如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,DF⊥AC于点F. 求证:AE=DF.
(
2题图
)
【当堂达标】
1.下列各句判定矩形的说法是否正确?为什么?
(1)四个角都相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)对角线相等,且有一个角是直角的四边形是矩形;
(4)两组对边分别平行,且对角线相等的四边形是矩形.
(
A
B
C
D
O
E
2题图
)2.已知矩形ABCD,对角线AC、BD相交于 AE、BE相交于E,试判定四边形OAEB的形状.
3.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
①求证:EO=FO;
(
3题图
)②当O点运动到何处时,四边形AECF是矩形?并证明你的结论.
【课后拓展】
(
图
2
)如图2,在平行四边形ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC,求证:四边形AFCE是矩形.
6.2矩形的性质与判断(3)
【知识梳理】
1.有一个角是直角的平行四边形
2.对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
【巩固练习】
1.B 2.C 3.C 4.D
5. 解:(证明:四边形为菱形,
∴,
∴,
∵,,
,,
在和中,
,
,
,
∴四边形为平 四边形,
,
∴为矩形.
6(1)证明:∵四边形ABCD是平行四边形,
∴DA∥CB,
∴∠EAF=∠EBC,
∵点E是边AB的中点,
∴AE=BE,
在△AEF和△BEC中,
∠EAF=∠ECB
AE=BE
∠AEF=∠BEC,
∴△AEF≌△BEC(ASA),
∴EF=EC,
又∵AE=BE,
∴四边形AFBC是平行四边形;
(2)解:当∠AEC的度数为100度时,四边形AFBC是矩形,
理由:∵四边形AFBC是矩形,
∴AB=CF,
∴EC=EB,
∴∠ECB=∠EBC,
∵四边形ABCD是平行四边形,∠D=50°,
∴∠D=∠EBC=50°,
∴∠ECB=50°,
∴∠AEC=∠ECB+∠EBC=50°+50°=100°,
故答案为:100.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
