7.2.3 平行线的性质 课件(共35张PPT) 2024-2025学年七年级数学下册(人教版2024)
文档属性
| 名称 | 7.2.3 平行线的性质 课件(共35张PPT) 2024-2025学年七年级数学下册(人教版2024) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 21:27:51 | ||
图片预览








文档简介
(共35张PPT)
人教版(2024)七年级数学下册 第七章 相交线与平行线
7.2 平行线
7.2.3 平行线的性质
第1课时 平行线的性质
目录
学习目标
01
情景导入
02
新知探究
03
课本例题
04
05
课本练习
06
分层练习
08
07
课本习题
课堂小结
学习目标
1. 掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.
2. 能够根据平行线的性质进行简单的推理.
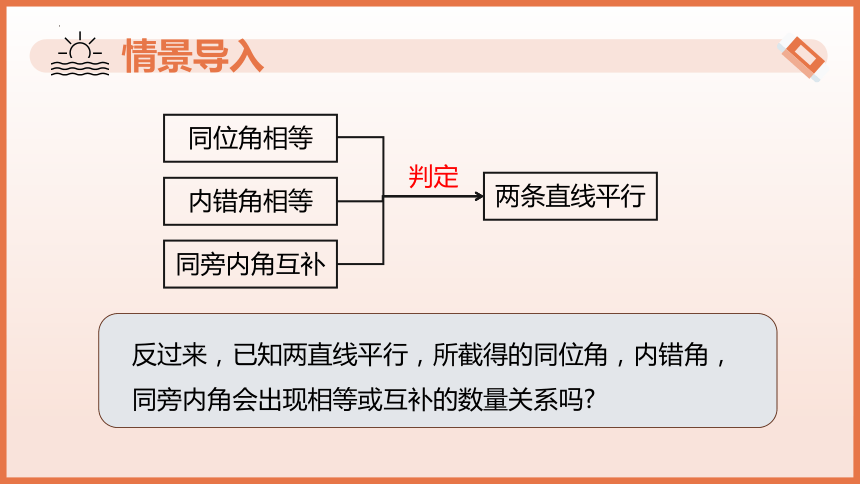
情景导入
反过来,已知两直线平行,所截得的同位角,内错角,同旁内角会出现相等或互补的数量关系吗
内错角相等
同位角相等
两条直线平行
同旁内角互补
判定
新知探究
如图,画两条平行线a∥ b,然后任意画一条截线c与这两条平行线相交,度量所形成的八个角的度数.
1
2
3
7
5
6
4
8
c
a
b
在∠1,∠2,…,∠8中,哪些是同位角?它们的度数有什么关系?由此猜想两条平行线被第三条直线截得的同位角有什么关系。
同位角:∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8.
猜想:两条平行线被第三条直线所截得的同位角相等.
利用信息技术工具改变截线c的位置,同样度量并比较各对同位角的度数,你的猜想还成立吗?
一般地,平行线具有性质:
性质1 两条平行直线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
思考
前面我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”.类似地,你能由性质1推出两条平行线被第三条直线截得的内错角之间的关系吗?
a
b
c
2
1
3
如右图,直线a∥ b,c是截线.根据 “两直线平行,同位角相等”,可得∠1=∠2.而∠3和∠2互为对顶角,所以∠3=∠2.所以∠3=∠1.这样就得到了平行线的另一个性质:
性质2 两条平行直线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
类似地,由性质1或性质2,可以推出平行线关于同旁内角的性质 (请你自己完成推理过程):
如图,已知 a//b,那么 2 与 4 有什么关系呢?
解: ∵a//b ,(已知)
∴ 1= 2.(两直线平行,同位角相等)
∵ 1+ 4=180°,(邻补角的性质)
∴ 2+ 4=180°.(等量代换)
a
b
c
2
1
4
性质3 两条平行直线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
例题讲解
解:因为梯形上、下两底DC与AB互相平行,根据“两直线平行,同旁内角互补”,可得∠A与∠D互补,∠B和∠C互补,于是
∠D=180°-∠A=180°-100°=80°,
∠C=180°-∠B=180°-115°=65°.
所以梯形的另外两个角∠D,∠C分别是80°,65°.
课本例题 例2
如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角∠D,∠C分别是多少度?
A
B
C
D
例题讲解
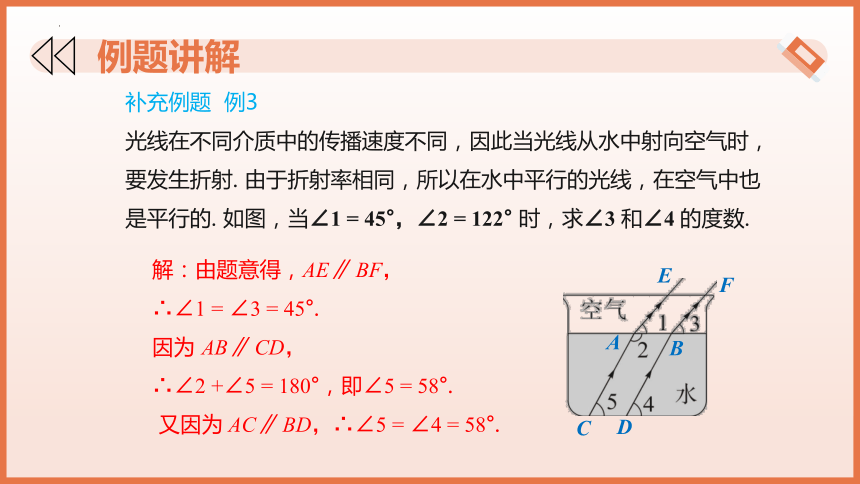
补充例题 例3
光线在不同介质中的传播速度不同,因此当光线从水中射向空气时,要发生折射. 由于折射率相同,所以在水中平行的光线,在空气中也是平行的. 如图,当∠1 = 45°,∠2 = 122° 时,求∠3 和∠4 的度数.
F
C
E
B
A
D
解:由题意得,AE∥ BF,
∴∠1 = ∠3 = 45°.
因为 AB∥ CD,
∴∠2 +∠5 = 180°,即∠5 = 58°.
又因为 AC∥ BD,∴∠5 = ∠4 = 58°.
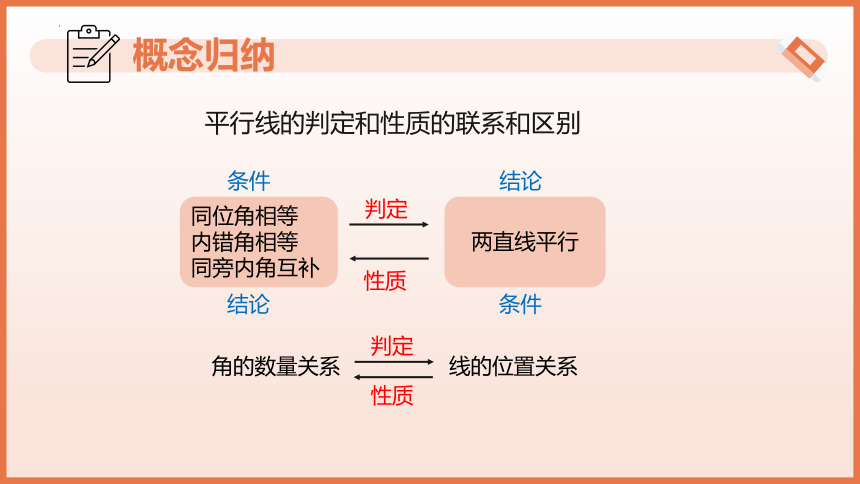
概念归纳
平行线的判定和性质的联系和区别
角的数量关系
线的位置关系
判定
性质
同位角相等
内错角相等
同旁内角互补
两直线平行
条件
结论
结论
条件
判定
性质
课堂练习
1. 如图,直线a // b,∠1=54°,∠2,∠3,∠4各是多少度?
解:∵a∥ b,∠1=54°,∴∠4 =∠1 = 54°
(两直线平行,同位角相等).
∠3 =180°-∠4=180° - 54°=126°,
∵∠2 与∠1 是对顶角,
∴∠2=∠1= 54°.
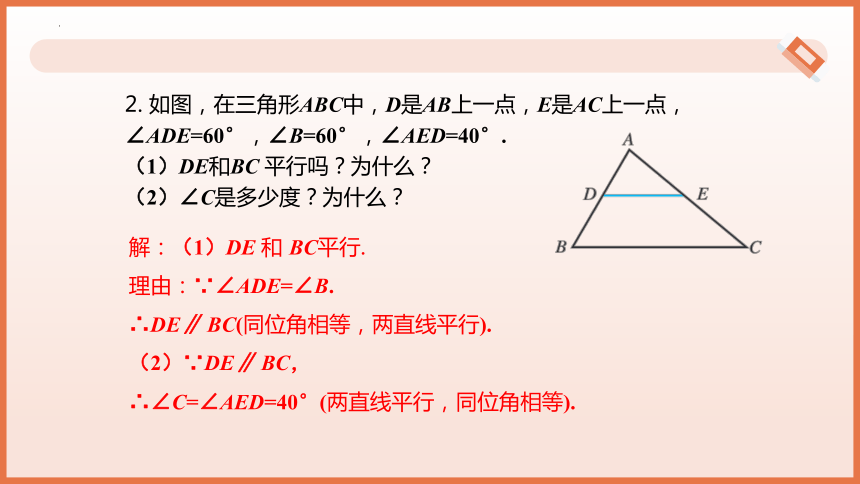
2. 如图,在三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°.
(1)DE和BC 平行吗?为什么?
(2)∠C是多少度?为什么?
解:(1)DE 和 BC平行.
理由:∵∠ADE=∠B.
∴DE∥ BC(同位角相等,两直线平行).
(2)∵DE∥ BC,
∴∠C=∠AED=40°(两直线平行,同位角相等).
3. 将一个直角三角尺与两边平行的纸条如图装置,则下列结论正确的是___________(填序号).
①∠1=∠2; ②∠4+∠5=180°;
③∠1+∠4=90°; ④∠4+90°=∠3.
①②③④
1
3
2
4
5
分层练习
1.如图,, ,则 的度数是( )
B
(第1题)
A. B.C. D.
基础题
(第2题)
2. [2024重庆] 如图, ,若
,则 的度数为( )
C
A. B. C. D.
(第3题)
3. [2024泸州] 把一块含 角的直角三角
尺按如图方式放置于两条平行线间,若
,则 ( )
B
A. B. C. D.
(第4题)
4. [2024·湖北] 如图,一条公路的两侧铺设
了, 两条平行管道,并有纵向管道
连通.若 ,则 的度数是
( )
B
A. B. C. D.
5.如图, ,下列结论正确的是( )
C
(第5题)
A.B.C.D.
(第6题)
6. [2024福建] 在同一平面内,将直尺、
含 角的三角尺和木工角尺
按如图方式摆放,若 ,
则 的大小为( )
A
A. B. C. D.
(第7题)
7. 如图,, , ,
则 的度数为( )
B
A.B.C. D.
8.如图,, , ,
则 等于 ______.
(第8题)
【点拨】如图所示,过点作 ,
, ,
, .
又 , ,
.
9.[2024·深圳龙岗区期中] 将一张等宽的纸条按如图所示的方式折叠,
若 ,则 的度数为______.
(第9题)
10.[2024·菏泽牡丹区期中] 如图,在四边形
中,,,那么与, 与
的关系如何?请说明理由.
解:, .
理由:, ,
, , ,
, .
11.如图,已知:平分,平分,且 .
试说明: .
【解】如图,
,
.
平分,平分 ,
, ,
.
.
综合应用题
12.如图,,.若 ,则 的度数为( )
A
(第12题)
A.B. C. D.
(第13题)
13. 一副三角尺按照如图方式摆放,其中
,,则 的度数为( )
C
A. B. C. D.
【点拨】设与交于点 .由题意可得
, , .
, ,
,
.
故选C.
(第14题)
14.如图,是的平分线,交
于点,交于点,若 ,
则 的度数为( )
C
A. B. C. D.
(第15题)
15.如图,,,则图中与
不包括 相等的角有( )
B
A.5个 B.4个 C.3个 D.2个
16. 已知两个角的两边分别平行,一个角为 ,另一个角为
,则满足题意的 的值是 ________.
30或70
(第17题)
17. 近几年中学生近视的现象越来越严重,为解决
这一问题,某公司推出了护眼灯,其侧面示意图
(台灯底座高度忽略不计)如图所示,其中,
,经使用发现,当 时,台灯光
线最佳,则此时 的度数为______.
(第18题)
18. 某些灯具的设计原理如图所示.从点照射到曲面灯罩
上的光线, 经灯罩反射后都沿着与直线在直线
上平行的方向射出.若 , ,
则____ .
60
[解析] 点拨:, .
,
.
, .
19.如图,若, ,
,,则 ______
(这里,均小于 ).
(第19题)
【点拨】如图,过点作 ,
.
又 ,
.
, . .
,
.
, ,
,
易得 .
(第20题)
20.如图,在三角形中, ,
,为线段 上一点,将三角形
沿直线折叠后,点落在 处,且
,则 的度数是____.
【点拨】 , ,
,由折叠的性质可
知, .又 ,
.
21.如图,已知平分, ,
,试说明:平分 .
解:平分, .
,, .
,, .
,平分 .
创新拓展题
22.[2024贵阳期中] 如图所示的是驱逐舰、巡洋舰两艘舰艇参
与某次演练的情景,已知 , .
(1)已知驱逐舰在方向上航行,巡洋舰在
方向上航行,假设在航行过程中各自航行方向保持
不变,试判断这两艘舰艇会不会相撞?请说明理由.
【解】不会相撞,理由:
, .
又 , ,
,
这两艘舰艇不会相撞.
(2)已知驱逐舰到达点后沿 继续航行,巡洋舰到达点后沿
继续航行,且, . 若驱逐舰在原航向上向左转动
后,才能与巡洋舰航向相同,求 的值.
22.[2024贵阳期中] 如图所示的是驱逐舰、巡洋舰
两艘舰艇参与某次演练的情景,已知 ,
.
【解】如图,过点作 ,此时驱逐舰与巡洋舰航向相同.
又 ,
, .
又 ,
.
23.
【提出问题】若两个角的两边分别平行,
则这两个角有怎样的数量关系?
【解决问题】 分两种情况进行探究,
请结合图①②探究这两个角的数量关系.
(1)如图①,,,试说明: ;
解:, ., .
(2)如图②,,,试说明: ;
解:, ., .
.
【得出结论】 由 我们可以得到结论:若两个角的两边分别平行,
则这两个角的数量关系为____________;
相等或互补
【拓展应用】(3)若两个角的两边分别平行,其中一个角比另一个角
的2倍少 ,求这两个角的度数.
23.
【提出问题】若两个角的两边分别平行,
则这两个角有怎样的数量关系?
[答案] 设其中一个角的度数为 ,则另一个角的度数为 ,
当 时,解得 .此时两个角的度数分别为 , ;
当 时,解得 .则 .
此时两个角的度数分别为 , .
综上,这两个角的度数分别是 , 或 , .
课堂小结
平行线的性质
性质 1
两直线平行,同位角_____
相等
性质 2
性质 3
两直线平行,内错角_____
相等
两直线平行,同旁内角_____
互补
人教版(2024)七年级数学下册 第七章 相交线与平行线
7.2 平行线
7.2.3 平行线的性质
第1课时 平行线的性质
目录
学习目标
01
情景导入
02
新知探究
03
课本例题
04
05
课本练习
06
分层练习
08
07
课本习题
课堂小结
学习目标
1. 掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.
2. 能够根据平行线的性质进行简单的推理.
情景导入
反过来,已知两直线平行,所截得的同位角,内错角,同旁内角会出现相等或互补的数量关系吗
内错角相等
同位角相等
两条直线平行
同旁内角互补
判定
新知探究
如图,画两条平行线a∥ b,然后任意画一条截线c与这两条平行线相交,度量所形成的八个角的度数.
1
2
3
7
5
6
4
8
c
a
b
在∠1,∠2,…,∠8中,哪些是同位角?它们的度数有什么关系?由此猜想两条平行线被第三条直线截得的同位角有什么关系。
同位角:∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8.
猜想:两条平行线被第三条直线所截得的同位角相等.
利用信息技术工具改变截线c的位置,同样度量并比较各对同位角的度数,你的猜想还成立吗?
一般地,平行线具有性质:
性质1 两条平行直线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
思考
前面我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”.类似地,你能由性质1推出两条平行线被第三条直线截得的内错角之间的关系吗?
a
b
c
2
1
3
如右图,直线a∥ b,c是截线.根据 “两直线平行,同位角相等”,可得∠1=∠2.而∠3和∠2互为对顶角,所以∠3=∠2.所以∠3=∠1.这样就得到了平行线的另一个性质:
性质2 两条平行直线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
类似地,由性质1或性质2,可以推出平行线关于同旁内角的性质 (请你自己完成推理过程):
如图,已知 a//b,那么 2 与 4 有什么关系呢?
解: ∵a//b ,(已知)
∴ 1= 2.(两直线平行,同位角相等)
∵ 1+ 4=180°,(邻补角的性质)
∴ 2+ 4=180°.(等量代换)
a
b
c
2
1
4
性质3 两条平行直线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
例题讲解
解:因为梯形上、下两底DC与AB互相平行,根据“两直线平行,同旁内角互补”,可得∠A与∠D互补,∠B和∠C互补,于是
∠D=180°-∠A=180°-100°=80°,
∠C=180°-∠B=180°-115°=65°.
所以梯形的另外两个角∠D,∠C分别是80°,65°.
课本例题 例2
如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角∠D,∠C分别是多少度?
A
B
C
D
例题讲解
补充例题 例3
光线在不同介质中的传播速度不同,因此当光线从水中射向空气时,要发生折射. 由于折射率相同,所以在水中平行的光线,在空气中也是平行的. 如图,当∠1 = 45°,∠2 = 122° 时,求∠3 和∠4 的度数.
F
C
E
B
A
D
解:由题意得,AE∥ BF,
∴∠1 = ∠3 = 45°.
因为 AB∥ CD,
∴∠2 +∠5 = 180°,即∠5 = 58°.
又因为 AC∥ BD,∴∠5 = ∠4 = 58°.
概念归纳
平行线的判定和性质的联系和区别
角的数量关系
线的位置关系
判定
性质
同位角相等
内错角相等
同旁内角互补
两直线平行
条件
结论
结论
条件
判定
性质
课堂练习
1. 如图,直线a // b,∠1=54°,∠2,∠3,∠4各是多少度?
解:∵a∥ b,∠1=54°,∴∠4 =∠1 = 54°
(两直线平行,同位角相等).
∠3 =180°-∠4=180° - 54°=126°,
∵∠2 与∠1 是对顶角,
∴∠2=∠1= 54°.
2. 如图,在三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°.
(1)DE和BC 平行吗?为什么?
(2)∠C是多少度?为什么?
解:(1)DE 和 BC平行.
理由:∵∠ADE=∠B.
∴DE∥ BC(同位角相等,两直线平行).
(2)∵DE∥ BC,
∴∠C=∠AED=40°(两直线平行,同位角相等).
3. 将一个直角三角尺与两边平行的纸条如图装置,则下列结论正确的是___________(填序号).
①∠1=∠2; ②∠4+∠5=180°;
③∠1+∠4=90°; ④∠4+90°=∠3.
①②③④
1
3
2
4
5
分层练习
1.如图,, ,则 的度数是( )
B
(第1题)
A. B.C. D.
基础题
(第2题)
2. [2024重庆] 如图, ,若
,则 的度数为( )
C
A. B. C. D.
(第3题)
3. [2024泸州] 把一块含 角的直角三角
尺按如图方式放置于两条平行线间,若
,则 ( )
B
A. B. C. D.
(第4题)
4. [2024·湖北] 如图,一条公路的两侧铺设
了, 两条平行管道,并有纵向管道
连通.若 ,则 的度数是
( )
B
A. B. C. D.
5.如图, ,下列结论正确的是( )
C
(第5题)
A.B.C.D.
(第6题)
6. [2024福建] 在同一平面内,将直尺、
含 角的三角尺和木工角尺
按如图方式摆放,若 ,
则 的大小为( )
A
A. B. C. D.
(第7题)
7. 如图,, , ,
则 的度数为( )
B
A.B.C. D.
8.如图,, , ,
则 等于 ______.
(第8题)
【点拨】如图所示,过点作 ,
, ,
, .
又 , ,
.
9.[2024·深圳龙岗区期中] 将一张等宽的纸条按如图所示的方式折叠,
若 ,则 的度数为______.
(第9题)
10.[2024·菏泽牡丹区期中] 如图,在四边形
中,,,那么与, 与
的关系如何?请说明理由.
解:, .
理由:, ,
, , ,
, .
11.如图,已知:平分,平分,且 .
试说明: .
【解】如图,
,
.
平分,平分 ,
, ,
.
.
综合应用题
12.如图,,.若 ,则 的度数为( )
A
(第12题)
A.B. C. D.
(第13题)
13. 一副三角尺按照如图方式摆放,其中
,,则 的度数为( )
C
A. B. C. D.
【点拨】设与交于点 .由题意可得
, , .
, ,
,
.
故选C.
(第14题)
14.如图,是的平分线,交
于点,交于点,若 ,
则 的度数为( )
C
A. B. C. D.
(第15题)
15.如图,,,则图中与
不包括 相等的角有( )
B
A.5个 B.4个 C.3个 D.2个
16. 已知两个角的两边分别平行,一个角为 ,另一个角为
,则满足题意的 的值是 ________.
30或70
(第17题)
17. 近几年中学生近视的现象越来越严重,为解决
这一问题,某公司推出了护眼灯,其侧面示意图
(台灯底座高度忽略不计)如图所示,其中,
,经使用发现,当 时,台灯光
线最佳,则此时 的度数为______.
(第18题)
18. 某些灯具的设计原理如图所示.从点照射到曲面灯罩
上的光线, 经灯罩反射后都沿着与直线在直线
上平行的方向射出.若 , ,
则____ .
60
[解析] 点拨:, .
,
.
, .
19.如图,若, ,
,,则 ______
(这里,均小于 ).
(第19题)
【点拨】如图,过点作 ,
.
又 ,
.
, . .
,
.
, ,
,
易得 .
(第20题)
20.如图,在三角形中, ,
,为线段 上一点,将三角形
沿直线折叠后,点落在 处,且
,则 的度数是____.
【点拨】 , ,
,由折叠的性质可
知, .又 ,
.
21.如图,已知平分, ,
,试说明:平分 .
解:平分, .
,, .
,, .
,平分 .
创新拓展题
22.[2024贵阳期中] 如图所示的是驱逐舰、巡洋舰两艘舰艇参
与某次演练的情景,已知 , .
(1)已知驱逐舰在方向上航行,巡洋舰在
方向上航行,假设在航行过程中各自航行方向保持
不变,试判断这两艘舰艇会不会相撞?请说明理由.
【解】不会相撞,理由:
, .
又 , ,
,
这两艘舰艇不会相撞.
(2)已知驱逐舰到达点后沿 继续航行,巡洋舰到达点后沿
继续航行,且, . 若驱逐舰在原航向上向左转动
后,才能与巡洋舰航向相同,求 的值.
22.[2024贵阳期中] 如图所示的是驱逐舰、巡洋舰
两艘舰艇参与某次演练的情景,已知 ,
.
【解】如图,过点作 ,此时驱逐舰与巡洋舰航向相同.
又 ,
, .
又 ,
.
23.
【提出问题】若两个角的两边分别平行,
则这两个角有怎样的数量关系?
【解决问题】 分两种情况进行探究,
请结合图①②探究这两个角的数量关系.
(1)如图①,,,试说明: ;
解:, ., .
(2)如图②,,,试说明: ;
解:, ., .
.
【得出结论】 由 我们可以得到结论:若两个角的两边分别平行,
则这两个角的数量关系为____________;
相等或互补
【拓展应用】(3)若两个角的两边分别平行,其中一个角比另一个角
的2倍少 ,求这两个角的度数.
23.
【提出问题】若两个角的两边分别平行,
则这两个角有怎样的数量关系?
[答案] 设其中一个角的度数为 ,则另一个角的度数为 ,
当 时,解得 .此时两个角的度数分别为 , ;
当 时,解得 .则 .
此时两个角的度数分别为 , .
综上,这两个角的度数分别是 , 或 , .
课堂小结
平行线的性质
性质 1
两直线平行,同位角_____
相等
性质 2
性质 3
两直线平行,内错角_____
相等
两直线平行,同旁内角_____
互补
同课章节目录
