6.1.2 平行四边形及其性质(第二课时)课件(共17张PPT) 2024-2025学年八年级数学下册(青岛版)
文档属性
| 名称 | 6.1.2 平行四边形及其性质(第二课时)课件(共17张PPT) 2024-2025学年八年级数学下册(青岛版) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 21:55:11 | ||
图片预览




文档简介
(共17张PPT)
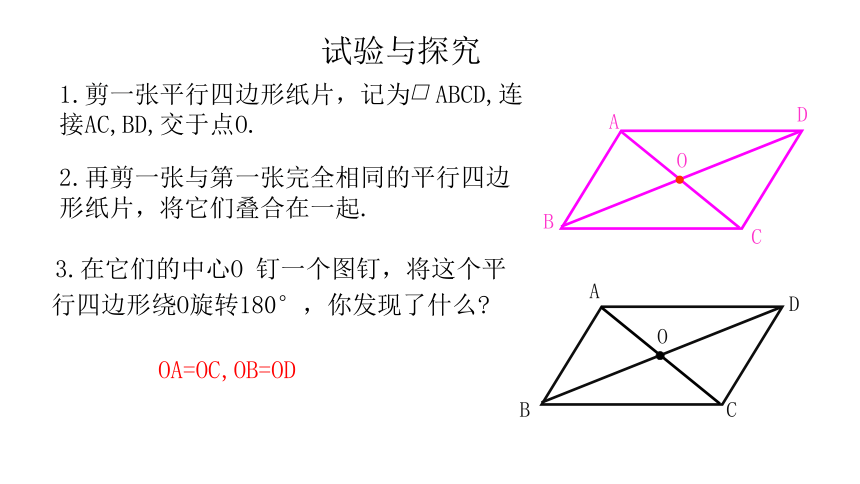
课堂导入
1.什么叫平行四边形?
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形具有哪些性质?
平行四边形的对边平行
平行四边形的对边相等
平行四边形的对角相等
边的性质
角的性质
平行四边形
对 角 线
性 质 ?
6.1 平行四边形及其性质
第六章 平行四边形
青岛版八年级数学下册
第 二 课 时
学习目标
1
2
掌握平行四边形对角线互相平分的性质,能综合应用平行四边形的性质解题
进一步发展合情推理能力,增强学生逻辑推理能力,使学生掌握说理的基本方法
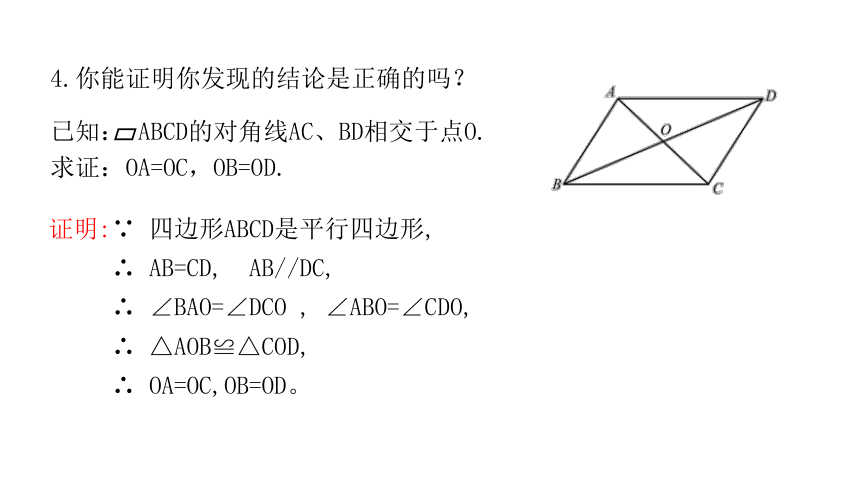
试验与探究
3.在它们的中心O 钉一个图钉,将这个平行四边形绕O旋转180°,你发现了什么
1.剪一张平行四边形纸片,记为 ABCD,连接AC,BD,交于点O.
A
B
D
C
O
2.再剪一张与第一张完全相同的平行四边形纸片,将它们叠合在一起.
O
D
C
B
A
OA=OC,OB=OD
已知: ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
4.你能证明你发现的结论是正确的吗?
证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD, AB//DC,
∴ ∠BAO=∠DCO , ∠ABO=∠CDO,
∴ △AOB≌△COD,
∴ OA=OC,OB=OD。
新知生成
平行四边形的对角线互相平分
平行四边形性质定理3
∵四边形ABCD是
∴OA=OC,OB=OD
证明线段相等
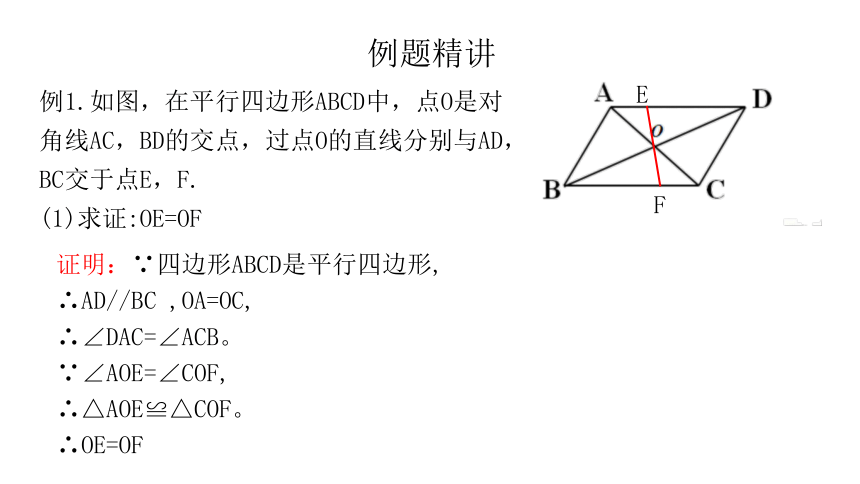
例题精讲
例1.如图,在平行四边形ABCD中,点O是对角线AC,BD的交点,过点O的直线分别与AD,BC交于点E,F.
(1)求证:OE=OF
E
F
证明:∵四边形ABCD是平行四边形,
∴AD//BC ,OA=OC,
∴∠DAC=∠ACB。
∵∠AOE=∠COF,
∴△AOE≌△COF。
∴OE=OF
(2)在上述问题中,若过点O的直线与边BA、DC的延长线交于点E、F,上述结论是否仍然成立?试说明理由。
E
F
证明:∵四边形ABCD是平行四边形,
∴AB//CD ,OA=OC,
∴∠E=∠F
∵∠AOE=∠COF,
∴△AOE≌△COF。
∴OE=OF
E
F
E
F
思考:
过点0的直线与平行四边形的位置关系还有吗?
OE与OF仍相等吗?
学习小心得
过平行四边形的对角线交点作直线,与平行四边形的一组对边或对边的延长线相交,所得到线段总被对角线的交点平分.
课堂练习(基础篇)
1.如图,在平行四边形ABCD中,BC=10cm, AC=8cm,BD=14cm, 求△ BOC的周长是多少?
21cm
2.如图,在平行四边形ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,求CD的长.
5
A
B
D
C
O
3.如图,在平行四边形ABCD中, 对角线AC﹑BD相交于点O,若△AOB,△AOD,△DOC,△COB的面积分别是S1,S2,S3,S4,试探究S1,S2,S3,S4,之间的关系.
S1=S2=S3=S4
平行四边形的两条对角线把平行四边形分成面积相等的四部分.
平行四边形的性质
课堂练习(能力篇)
1.如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,求AD的取值范围。
1<AD<9
2.在平行四边形ABCD中,E、F在AC上,四边形DEBF是平行四边形.
求证:AE=CF.
思路点拨:通过证明△ADE≌△CBF即可。
3.在平行四边形ABCD中,周长为20cm,对角线AC交BD于点O,△OBC比△OAB的周长多4,求AB与BC的长度。
AB=3cm,BC=7cm
4.在平行四边形ABCD中,对角线AC与BD交于点O,E为OB中点,F为OD中点.
(1)图中共有 对全等三角形
(2)试探究OE与OF具有什么数量关系,说明理由.
(3)若把条件“E为OB中点,F为OD中点”改为“AE┴BD,CF┴BD”,则上述结论还成立吗?
6
仍成立
OE=OF
课堂小结
你的收获是……
你的疑惑是……
你的建议是……
课堂检测
(2)若△AOB的周长为30cm, AB=12cm,则对角线AC与BD的和是 。
(1)平行四边形具有而一般四边形不具有 的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360° D、外角和为360°
B
36cm
A
B
D
C
O
E
(3)已知在平行四边形ABCD中,其周长是12,点O是对角线AC,BD的交点,EOBD,连接DE,求△ABE的周长.
6
课下作业
必做题:
(1)课本188页习题5.6第9题
(2)课本188页习题5.6第10题
选做题:课本186页课后练习第2题
课堂导入
1.什么叫平行四边形?
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形具有哪些性质?
平行四边形的对边平行
平行四边形的对边相等
平行四边形的对角相等
边的性质
角的性质
平行四边形
对 角 线
性 质 ?
6.1 平行四边形及其性质
第六章 平行四边形
青岛版八年级数学下册
第 二 课 时
学习目标
1
2
掌握平行四边形对角线互相平分的性质,能综合应用平行四边形的性质解题
进一步发展合情推理能力,增强学生逻辑推理能力,使学生掌握说理的基本方法
试验与探究
3.在它们的中心O 钉一个图钉,将这个平行四边形绕O旋转180°,你发现了什么
1.剪一张平行四边形纸片,记为 ABCD,连接AC,BD,交于点O.
A
B
D
C
O
2.再剪一张与第一张完全相同的平行四边形纸片,将它们叠合在一起.
O
D
C
B
A
OA=OC,OB=OD
已知: ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
4.你能证明你发现的结论是正确的吗?
证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD, AB//DC,
∴ ∠BAO=∠DCO , ∠ABO=∠CDO,
∴ △AOB≌△COD,
∴ OA=OC,OB=OD。
新知生成
平行四边形的对角线互相平分
平行四边形性质定理3
∵四边形ABCD是
∴OA=OC,OB=OD
证明线段相等
例题精讲
例1.如图,在平行四边形ABCD中,点O是对角线AC,BD的交点,过点O的直线分别与AD,BC交于点E,F.
(1)求证:OE=OF
E
F
证明:∵四边形ABCD是平行四边形,
∴AD//BC ,OA=OC,
∴∠DAC=∠ACB。
∵∠AOE=∠COF,
∴△AOE≌△COF。
∴OE=OF
(2)在上述问题中,若过点O的直线与边BA、DC的延长线交于点E、F,上述结论是否仍然成立?试说明理由。
E
F
证明:∵四边形ABCD是平行四边形,
∴AB//CD ,OA=OC,
∴∠E=∠F
∵∠AOE=∠COF,
∴△AOE≌△COF。
∴OE=OF
E
F
E
F
思考:
过点0的直线与平行四边形的位置关系还有吗?
OE与OF仍相等吗?
学习小心得
过平行四边形的对角线交点作直线,与平行四边形的一组对边或对边的延长线相交,所得到线段总被对角线的交点平分.
课堂练习(基础篇)
1.如图,在平行四边形ABCD中,BC=10cm, AC=8cm,BD=14cm, 求△ BOC的周长是多少?
21cm
2.如图,在平行四边形ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,求CD的长.
5
A
B
D
C
O
3.如图,在平行四边形ABCD中, 对角线AC﹑BD相交于点O,若△AOB,△AOD,△DOC,△COB的面积分别是S1,S2,S3,S4,试探究S1,S2,S3,S4,之间的关系.
S1=S2=S3=S4
平行四边形的两条对角线把平行四边形分成面积相等的四部分.
平行四边形的性质
课堂练习(能力篇)
1.如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,求AD的取值范围。
1<AD<9
2.在平行四边形ABCD中,E、F在AC上,四边形DEBF是平行四边形.
求证:AE=CF.
思路点拨:通过证明△ADE≌△CBF即可。
3.在平行四边形ABCD中,周长为20cm,对角线AC交BD于点O,△OBC比△OAB的周长多4,求AB与BC的长度。
AB=3cm,BC=7cm
4.在平行四边形ABCD中,对角线AC与BD交于点O,E为OB中点,F为OD中点.
(1)图中共有 对全等三角形
(2)试探究OE与OF具有什么数量关系,说明理由.
(3)若把条件“E为OB中点,F为OD中点”改为“AE┴BD,CF┴BD”,则上述结论还成立吗?
6
仍成立
OE=OF
课堂小结
你的收获是……
你的疑惑是……
你的建议是……
课堂检测
(2)若△AOB的周长为30cm, AB=12cm,则对角线AC与BD的和是 。
(1)平行四边形具有而一般四边形不具有 的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360° D、外角和为360°
B
36cm
A
B
D
C
O
E
(3)已知在平行四边形ABCD中,其周长是12,点O是对角线AC,BD的交点,EOBD,连接DE,求△ABE的周长.
6
课下作业
必做题:
(1)课本188页习题5.6第9题
(2)课本188页习题5.6第10题
选做题:课本186页课后练习第2题
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
