人教版(2024)七年级下册 7.1.2两条直线垂直 课件(共32张PPT)
文档属性
| 名称 | 人教版(2024)七年级下册 7.1.2两条直线垂直 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 15.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 22:41:21 | ||
图片预览








文档简介
(共32张PPT)
7.1.2两条直线垂直
第七章 相交线与平行线
人教版(2024)
素养目标
1.了解垂线、垂线段的概念,能过一点作已知直线的垂线;
4.初步形成几何概念的认识方式和几何结论的归纳方法.
3.理解并掌握垂线的性质,能利用垂线的定义计算角的度数;
重点
2.理解点到直线的距离的意义,能度量点到直线的距离;
重点
难点
知识回顾
邻补角
对顶角
位置关系
数量关系
互补
相等
两条直线相交形成几个角?这些角之间有什么关系?
O
B
A
D
C
1
2
3
4
∠1和∠2,∠2和∠3
∠3和∠4,∠4和∠1
∠1和∠3,∠2和∠4
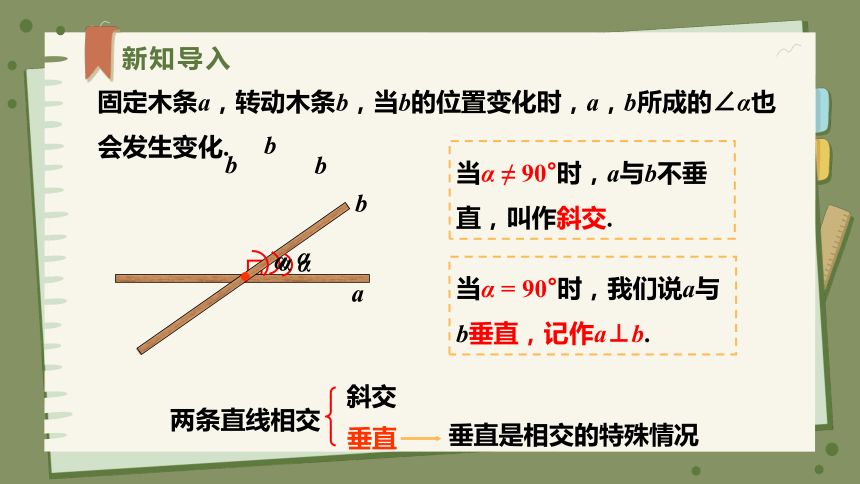
新知导入
固定木条a,转动木条b,当b的位置变化时,a,b所成的∠α也会发生变化.
α
a
b
当α = 90°时,我们说a与b垂直,记作a⊥b.
α
α
α
b
b
b
当α ≠ 90°时,a与b不垂直,叫作斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
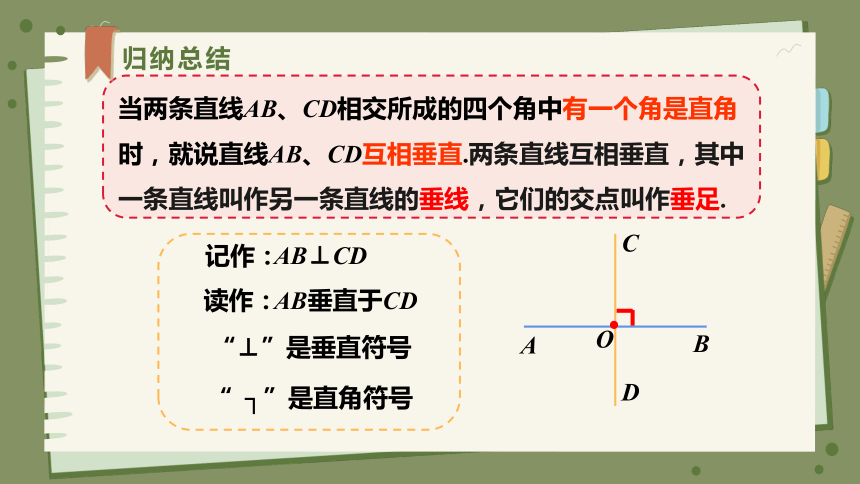
归纳总结
当两条直线AB、CD相交所成的四个角中有一个角是直角时,就说直线AB、CD互相垂直.两条直线互相垂直,其中一条直线叫作另一条直线的垂线,它们的交点叫作垂足.
记作:
AB⊥CD
“⊥”是垂直符号
“ ┐”是直角符号
读作:
AB垂直于CD
O
D
C
B
A
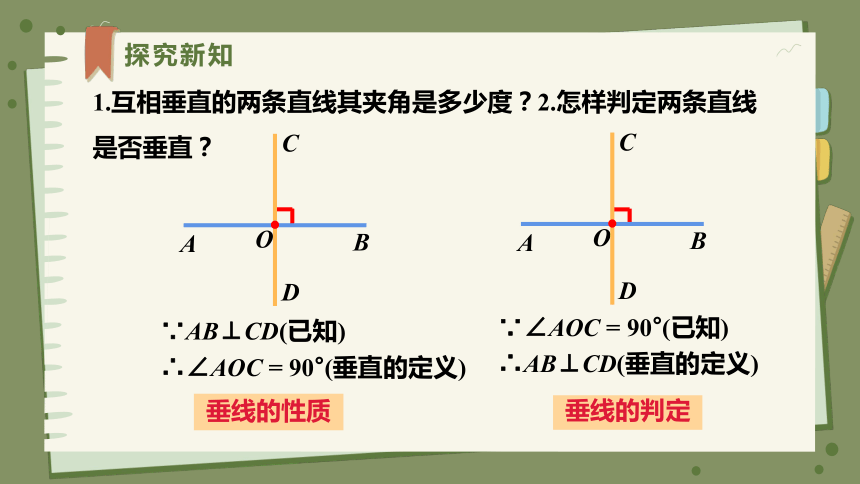
探究新知
∵AB⊥CD(已知)
∴∠AOC = 90°(垂直的定义)
∵∠AOC = 90°(已知)
∴AB⊥CD(垂直的定义)
1.互相垂直的两条直线其夹角是多少度?2.怎样判定两条直线是否垂直?
垂线的性质
垂线的判定
O
D
C
B
A
O
D
C
B
A
归纳总结
垂直的定义具有双重作用:
①知线垂直得直角;
②知直角得线垂直.
如图,①若 AB⊥CD,
则∠BOC =∠AOC =∠AOD =∠BOD =90°;
②若∠BOC =90°,则 AB⊥CD.
O
D
C
B
A
图片欣赏
在日常生活中,两条直线互相垂直的情形很常见,欣赏下面图片找到互相垂直的线.
探究新知
用三角尺或量角器画已知直线 l 的垂线,这样的垂线能画出几条?
无数条
l
… …
… …
探究新知
过直线 l 上一点 A 画直线 l 的垂线,这样的垂线能画出几条?
A
l
A
l
有且只有一条
1.落.
2.移.
3.画.
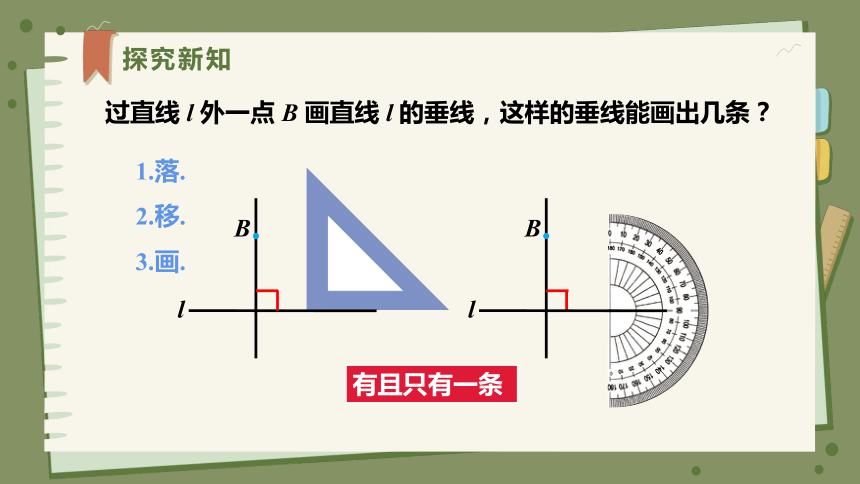
探究新知
过直线 l 外一点 B 画直线 l 的垂线,这样的垂线能画出几条?
B
l
B
l
有且只有一条
1.落.
2.移.
3.画.
归纳总结
垂线的画法
1.落:让三角尺的一条直角边落在已知直线上,使其与已知直线重合.
2.移:沿已知直线移动三角尺,使其另一条直角边经过已知点.
3.画:沿此直角边画直线,则这条直线就是已知直线的垂线.
垂线的性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.
存在且唯一
例题练习
如图,过点 P 画出射线 AB 或线段 AB 的垂线.
A
B
P
(1)
A
B
P
(2)
A
B
P
(3)
画一条射线或线段的垂线,就是画它们所在直线的垂线.
探究新知
PO=1.8cm
PA1=1.9cm
PA2=2.1cm
PA3=2.6cm
从直线外一点引一条直线的垂线,这点和垂足之间的线段叫做垂线段.
连接直线外一点与直线上各点的所有线段中,垂线段最短.
P
l
O
A1
A2
A3
…
比较线段PO,PA1,PA2,PA3的长短,这些线段中,哪一条最短?
归纳总结
垂线的性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.简单说成:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
如图,线段 AD 的长度是点 A 到
直线 l 的距离.
C
D
E
l
B
A
归纳总结
注意:
(1)连接直线外一点与直线上各点有无数条线段,但垂线段只有一条.
(2)垂线是一条直线,长度不可以度量,而垂线段是一条线段,长度可以度量.
(3)垂线段是几何图形,而点到直线的距离是点到直线的垂线段的长度,是一个数量.
练一练
如图,在灌溉时,要把河中的水引到农田P 处,如何让挖渠能使渠道最短?
垂线段最短.
Q
垂线段最短
120°
C
43°
B
小结
垂线
垂线的定义
垂线的性质
在同一平面内,过一点
______________直线与已知直线垂直
垂线段__ __
垂线的画法
一落二移三画
最短
点到直线的距离
有且只有一条
谢谢同学们的聆听
7.1.2两条直线垂直
第七章 相交线与平行线
人教版(2024)
素养目标
1.了解垂线、垂线段的概念,能过一点作已知直线的垂线;
4.初步形成几何概念的认识方式和几何结论的归纳方法.
3.理解并掌握垂线的性质,能利用垂线的定义计算角的度数;
重点
2.理解点到直线的距离的意义,能度量点到直线的距离;
重点
难点
知识回顾
邻补角
对顶角
位置关系
数量关系
互补
相等
两条直线相交形成几个角?这些角之间有什么关系?
O
B
A
D
C
1
2
3
4
∠1和∠2,∠2和∠3
∠3和∠4,∠4和∠1
∠1和∠3,∠2和∠4
新知导入
固定木条a,转动木条b,当b的位置变化时,a,b所成的∠α也会发生变化.
α
a
b
当α = 90°时,我们说a与b垂直,记作a⊥b.
α
α
α
b
b
b
当α ≠ 90°时,a与b不垂直,叫作斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
归纳总结
当两条直线AB、CD相交所成的四个角中有一个角是直角时,就说直线AB、CD互相垂直.两条直线互相垂直,其中一条直线叫作另一条直线的垂线,它们的交点叫作垂足.
记作:
AB⊥CD
“⊥”是垂直符号
“ ┐”是直角符号
读作:
AB垂直于CD
O
D
C
B
A
探究新知
∵AB⊥CD(已知)
∴∠AOC = 90°(垂直的定义)
∵∠AOC = 90°(已知)
∴AB⊥CD(垂直的定义)
1.互相垂直的两条直线其夹角是多少度?2.怎样判定两条直线是否垂直?
垂线的性质
垂线的判定
O
D
C
B
A
O
D
C
B
A
归纳总结
垂直的定义具有双重作用:
①知线垂直得直角;
②知直角得线垂直.
如图,①若 AB⊥CD,
则∠BOC =∠AOC =∠AOD =∠BOD =90°;
②若∠BOC =90°,则 AB⊥CD.
O
D
C
B
A
图片欣赏
在日常生活中,两条直线互相垂直的情形很常见,欣赏下面图片找到互相垂直的线.
探究新知
用三角尺或量角器画已知直线 l 的垂线,这样的垂线能画出几条?
无数条
l
… …
… …
探究新知
过直线 l 上一点 A 画直线 l 的垂线,这样的垂线能画出几条?
A
l
A
l
有且只有一条
1.落.
2.移.
3.画.
探究新知
过直线 l 外一点 B 画直线 l 的垂线,这样的垂线能画出几条?
B
l
B
l
有且只有一条
1.落.
2.移.
3.画.
归纳总结
垂线的画法
1.落:让三角尺的一条直角边落在已知直线上,使其与已知直线重合.
2.移:沿已知直线移动三角尺,使其另一条直角边经过已知点.
3.画:沿此直角边画直线,则这条直线就是已知直线的垂线.
垂线的性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.
存在且唯一
例题练习
如图,过点 P 画出射线 AB 或线段 AB 的垂线.
A
B
P
(1)
A
B
P
(2)
A
B
P
(3)
画一条射线或线段的垂线,就是画它们所在直线的垂线.
探究新知
PO=1.8cm
PA1=1.9cm
PA2=2.1cm
PA3=2.6cm
从直线外一点引一条直线的垂线,这点和垂足之间的线段叫做垂线段.
连接直线外一点与直线上各点的所有线段中,垂线段最短.
P
l
O
A1
A2
A3
…
比较线段PO,PA1,PA2,PA3的长短,这些线段中,哪一条最短?
归纳总结
垂线的性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.简单说成:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
如图,线段 AD 的长度是点 A 到
直线 l 的距离.
C
D
E
l
B
A
归纳总结
注意:
(1)连接直线外一点与直线上各点有无数条线段,但垂线段只有一条.
(2)垂线是一条直线,长度不可以度量,而垂线段是一条线段,长度可以度量.
(3)垂线段是几何图形,而点到直线的距离是点到直线的垂线段的长度,是一个数量.
练一练
如图,在灌溉时,要把河中的水引到农田P 处,如何让挖渠能使渠道最短?
垂线段最短.
Q
垂线段最短
120°
C
43°
B
小结
垂线
垂线的定义
垂线的性质
在同一平面内,过一点
______________直线与已知直线垂直
垂线段__ __
垂线的画法
一落二移三画
最短
点到直线的距离
有且只有一条
谢谢同学们的聆听
同课章节目录
