2024-2025学年湘教版数学九年级下册2.6弧长与扇形面积(2)(共21张PPT)
文档属性
| 名称 | 2024-2025学年湘教版数学九年级下册2.6弧长与扇形面积(2)(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 22:54:52 | ||
图片预览





文档简介
(共21张PPT)
2.6 弧长与扇形面积(2)
主讲:
湘教版数学九年级下册
第2章 圆
有风不动无风动,
不动无风动有风.
猜迷
(打一夏季常用生活用品)
观察下图中图形,它们的有什么共同点。
都像扇子
导入新课
学习目标
目标
1
目标
2
1. 认识扇形,知道扇形的概念;
2. 能推导并记住扇形的面积公式(重点)
3. 会求扇形以及与圆、扇形有关的组合图形的面积(难点)
目标
3
自学指导
阅读教材P79-80。用5分钟的时间看谁又快又好地解决以下问题:
1、看书P79探究的上面部分,知道什么叫扇形,了解在同圆中,圆心角与扇形面积的关系;
2、看P79的“探究”,理解并记住1度的圆心角的扇形面积是多少,从而熟记扇形的面积计算公式;
3、看P79的例3,学会计算扇形的面积,看P80的例4,学会用扇形面积计算圆弧形弯道的面积,并掌握做题的格式与步骤。
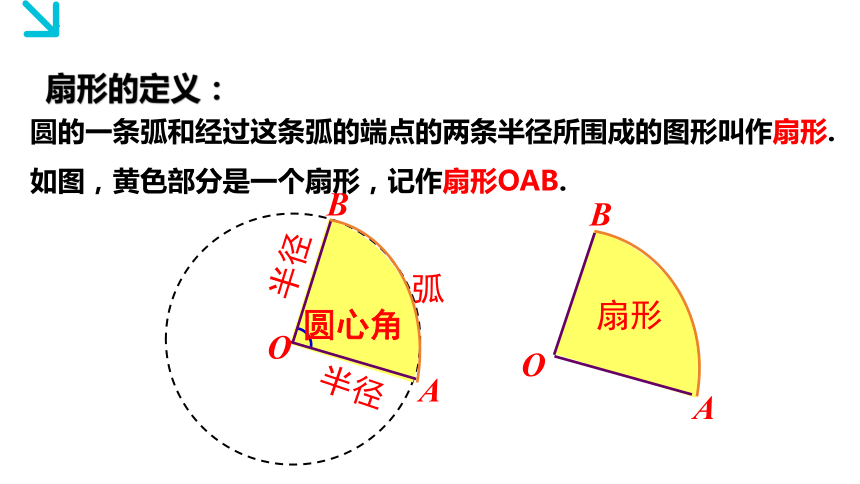
扇形的定义:
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
如图,黄色部分是一个扇形,记作扇形OAB.
探究新知
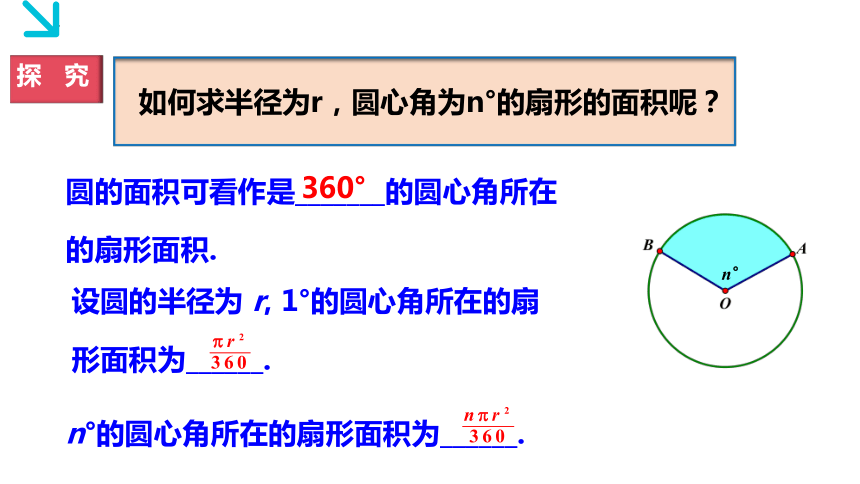
如何求半径为r,圆心角为n°的扇形的面积呢?
探究新知
探 究
圆的面积可看作是_______的圆心角所在的扇形面积.
设圆的半径为 r, 1°的圆心角所在的扇形面积为______.
n°的圆心角所在的扇形面积为______.
360°
n°
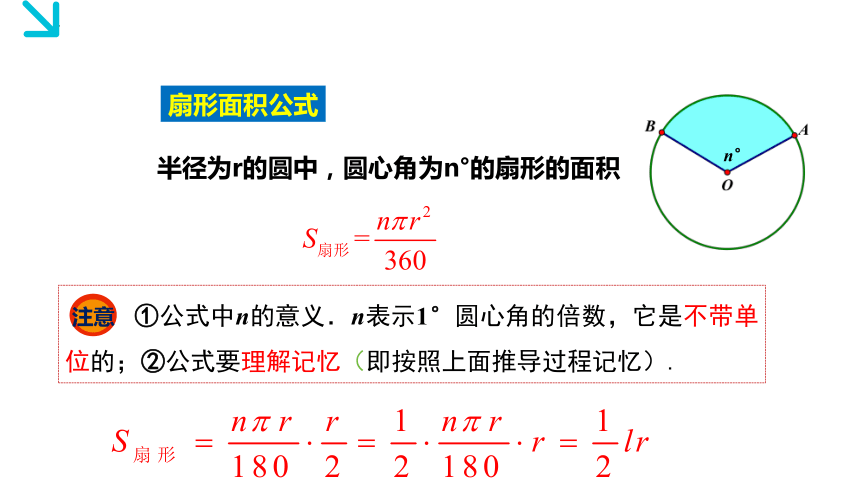
扇形面积公式
半径为r的圆中,圆心角为n°的扇形的面积
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).
注意
n°
探究新知
例题讲解
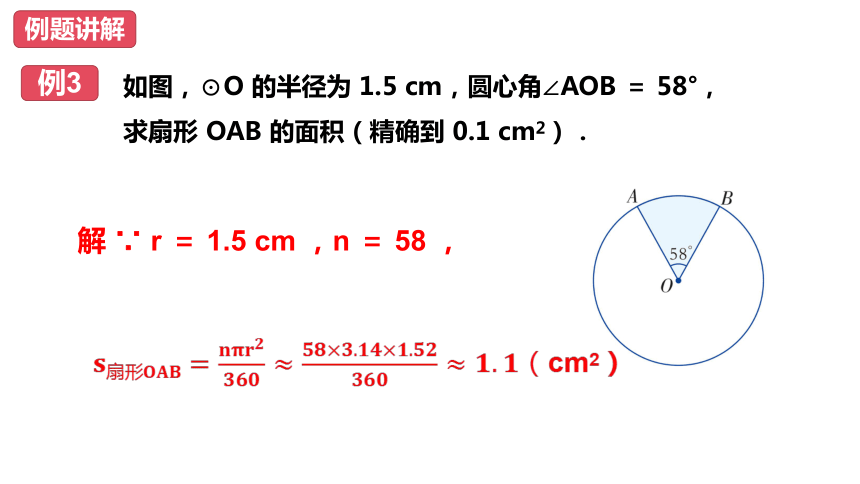
例3
如图,⊙O 的半径为 1.5 cm,圆心角∠AOB = 58°,求扇形 OAB 的面积(精确到 0.1 cm2).
解 ∵ r = 1.5 cm ,n = 58 ,
cm2)
例题讲解
例4
如图是一条圆弧形弯道,已知OA=20m,OC=12m,
的长度为9πm,求圆弧形弯道的面积.
解:设∠AOB = n°,
∵ OC = 12 m,CD的长度为 9π m,
∴
解得 n = 135,即圆心角∠COD = 135 ° .
∴m2)
m2)
∴S扇形ACDB = S扇形OAB - S扇形OCD = 150π - 54π = 96π(m2)
答:这条圆弧形弯道的面积为 96π m2.
基础检测
1.一个扇形的弧长为20πcm,半径为24cm,则该扇形的面积为_______.
2. 扇形的圆心角为60°,半径为5 ,则这个扇形的弧长_______, 这个扇形的面积为______.
3.已知扇形的圆心角为120°,弧长为20π,扇形面积为 .
4、扇形的圆心角为72°,面积为5π,则此扇形的弧长为________.
2π
【分析】设半径为R,
∵扇形的圆心角为72°,面积为5π,
∴5π=,解得:R=5,
法一:
∴l==2π.
法二:
∴5π=·l·5,解得:l=2π.
基础检测
5、如图,将半径为2cm的圆形纸片翻折,使得,恰好都经过圆心O,折痕为AB,BC,则阴影部分的面积为________.
π
【分析】如图,作OD⊥AB于点D,连接AO,BO,CO,
∵OD=AO,∴∠OAD=30°,∠AOD=60°,
∴∠AOB=2∠AOD=120°,
同理:∠BOC=120°,∴∠AOC=120°,
∴阴影部分的面积=S扇形AOC==π(cm2).
割补法
基础检测
基础检测
6.如图,半径为1cm、圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )
A.πcm2 B. πcm2
C. cm2 D. cm2
C
如图,在⊙O 中,∠AOB = 120°,弦 AB 的长为 cm, 求扇形 OAB 的面积.
一展身手
解:作OD⊥AB.
∵ OA=OB,
∴ AD=AB=,∠AOD= ∠AOB=60°.
∴ OA=.
∴
2. 如图,分别以△ABC 的顶点 A,B,C 为圆心,
以 1 为半径画圆,求图中绿色部分的面积.
解:∠A+ ∠B+ ∠C = 180°
绿色部分可以看成半径为 1,圆心角为180°的扇形.
一展身手
3. 如图,有一直径是 20 cm 的圆形纸片,现从中剪出一个圆心角是 90°的扇形 ABC,求被剪掉部分的面积.
解:连接BC,则 BC = 20 cm
又因为 AB = AC, 所以△ABC为等腰直角三角形.
AB=
答:被剪掉部分的面积为50 cm2.
一展身手
4、 已知正三角形 ABC 的边长为 a,D,E,F 分别为 BC,CA,AB 的中点分别以 A,B,C 为圆心,长为半径作圆,求图中阴影部分的面积.
解:连接 AD .
由题意得:CD = ,AC = a .∴ AD =
∴S△ABC = BC×AD× = ,
一展身手
挑战自我
1.如图,扇形的圆心角为90°,半径OC=2,∠AOC=30°,
CD⊥OB于点D,求阴影部分的面积.
解:∵∠AOB=90°,∠AOC=30°,
∴∠BOC=60°.
∵CD⊥OB,
∴∠CDO=90°,
∴OD=OC=1,CD=OD=,
∴阴影部分的面积=S扇形BOC -S△COD=×1×π-.
2.如图,AB为⊙O的直径,点C,D在⊙O上,且BC=6 cm,AC=8 cm,∠ABD=45°.
(1)求BD的长;(2)求图中阴影部分的面积.
解 (1)∵AB为⊙O的直径,
∴∠ACB=90°.
∵BC=6 cm,AC=8 cm,
∴AB=10 cm,∴OB=5 cm.
连接OD.
∵OD=OB,
∴∠ODB=∠ABD=45°,
∴∠BOD=90°,
(2)S阴影=S扇形-S△OBD
= π·52- ×5×5
360
90
2
1
= (cm2).
25π-50
4
∴BD2=OB2+OD2, BD= cm.
挑战自我
扇形
定义
公式
阴影部分面积求法
割补法
整体思想
课堂小结
主讲:
感谢聆听
湘教版九年级下册
2.6 弧长与扇形面积(2)
主讲:
湘教版数学九年级下册
第2章 圆
有风不动无风动,
不动无风动有风.
猜迷
(打一夏季常用生活用品)
观察下图中图形,它们的有什么共同点。
都像扇子
导入新课
学习目标
目标
1
目标
2
1. 认识扇形,知道扇形的概念;
2. 能推导并记住扇形的面积公式(重点)
3. 会求扇形以及与圆、扇形有关的组合图形的面积(难点)
目标
3
自学指导
阅读教材P79-80。用5分钟的时间看谁又快又好地解决以下问题:
1、看书P79探究的上面部分,知道什么叫扇形,了解在同圆中,圆心角与扇形面积的关系;
2、看P79的“探究”,理解并记住1度的圆心角的扇形面积是多少,从而熟记扇形的面积计算公式;
3、看P79的例3,学会计算扇形的面积,看P80的例4,学会用扇形面积计算圆弧形弯道的面积,并掌握做题的格式与步骤。
扇形的定义:
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
如图,黄色部分是一个扇形,记作扇形OAB.
探究新知
如何求半径为r,圆心角为n°的扇形的面积呢?
探究新知
探 究
圆的面积可看作是_______的圆心角所在的扇形面积.
设圆的半径为 r, 1°的圆心角所在的扇形面积为______.
n°的圆心角所在的扇形面积为______.
360°
n°
扇形面积公式
半径为r的圆中,圆心角为n°的扇形的面积
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).
注意
n°
探究新知
例题讲解
例3
如图,⊙O 的半径为 1.5 cm,圆心角∠AOB = 58°,求扇形 OAB 的面积(精确到 0.1 cm2).
解 ∵ r = 1.5 cm ,n = 58 ,
cm2)
例题讲解
例4
如图是一条圆弧形弯道,已知OA=20m,OC=12m,
的长度为9πm,求圆弧形弯道的面积.
解:设∠AOB = n°,
∵ OC = 12 m,CD的长度为 9π m,
∴
解得 n = 135,即圆心角∠COD = 135 ° .
∴m2)
m2)
∴S扇形ACDB = S扇形OAB - S扇形OCD = 150π - 54π = 96π(m2)
答:这条圆弧形弯道的面积为 96π m2.
基础检测
1.一个扇形的弧长为20πcm,半径为24cm,则该扇形的面积为_______.
2. 扇形的圆心角为60°,半径为5 ,则这个扇形的弧长_______, 这个扇形的面积为______.
3.已知扇形的圆心角为120°,弧长为20π,扇形面积为 .
4、扇形的圆心角为72°,面积为5π,则此扇形的弧长为________.
2π
【分析】设半径为R,
∵扇形的圆心角为72°,面积为5π,
∴5π=,解得:R=5,
法一:
∴l==2π.
法二:
∴5π=·l·5,解得:l=2π.
基础检测
5、如图,将半径为2cm的圆形纸片翻折,使得,恰好都经过圆心O,折痕为AB,BC,则阴影部分的面积为________.
π
【分析】如图,作OD⊥AB于点D,连接AO,BO,CO,
∵OD=AO,∴∠OAD=30°,∠AOD=60°,
∴∠AOB=2∠AOD=120°,
同理:∠BOC=120°,∴∠AOC=120°,
∴阴影部分的面积=S扇形AOC==π(cm2).
割补法
基础检测
基础检测
6.如图,半径为1cm、圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )
A.πcm2 B. πcm2
C. cm2 D. cm2
C
如图,在⊙O 中,∠AOB = 120°,弦 AB 的长为 cm, 求扇形 OAB 的面积.
一展身手
解:作OD⊥AB.
∵ OA=OB,
∴ AD=AB=,∠AOD= ∠AOB=60°.
∴ OA=.
∴
2. 如图,分别以△ABC 的顶点 A,B,C 为圆心,
以 1 为半径画圆,求图中绿色部分的面积.
解:∠A+ ∠B+ ∠C = 180°
绿色部分可以看成半径为 1,圆心角为180°的扇形.
一展身手
3. 如图,有一直径是 20 cm 的圆形纸片,现从中剪出一个圆心角是 90°的扇形 ABC,求被剪掉部分的面积.
解:连接BC,则 BC = 20 cm
又因为 AB = AC, 所以△ABC为等腰直角三角形.
AB=
答:被剪掉部分的面积为50 cm2.
一展身手
4、 已知正三角形 ABC 的边长为 a,D,E,F 分别为 BC,CA,AB 的中点分别以 A,B,C 为圆心,长为半径作圆,求图中阴影部分的面积.
解:连接 AD .
由题意得:CD = ,AC = a .∴ AD =
∴S△ABC = BC×AD× = ,
一展身手
挑战自我
1.如图,扇形的圆心角为90°,半径OC=2,∠AOC=30°,
CD⊥OB于点D,求阴影部分的面积.
解:∵∠AOB=90°,∠AOC=30°,
∴∠BOC=60°.
∵CD⊥OB,
∴∠CDO=90°,
∴OD=OC=1,CD=OD=,
∴阴影部分的面积=S扇形BOC -S△COD=×1×π-.
2.如图,AB为⊙O的直径,点C,D在⊙O上,且BC=6 cm,AC=8 cm,∠ABD=45°.
(1)求BD的长;(2)求图中阴影部分的面积.
解 (1)∵AB为⊙O的直径,
∴∠ACB=90°.
∵BC=6 cm,AC=8 cm,
∴AB=10 cm,∴OB=5 cm.
连接OD.
∵OD=OB,
∴∠ODB=∠ABD=45°,
∴∠BOD=90°,
(2)S阴影=S扇形-S△OBD
= π·52- ×5×5
360
90
2
1
= (cm2).
25π-50
4
∴BD2=OB2+OD2, BD= cm.
挑战自我
扇形
定义
公式
阴影部分面积求法
割补法
整体思想
课堂小结
主讲:
感谢聆听
湘教版九年级下册
