1.3 乘法公式第2课时 2024-2025学年七年级数学下册(共23张PPT)
文档属性
| 名称 | 1.3 乘法公式第2课时 2024-2025学年七年级数学下册(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 504.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 08:50:37 | ||
图片预览






文档简介
(共23张PPT)
1.3 乘法公式
第1章 整式的乘除
第2课时
北师大版(2024) 七年级 下册
学习目标
1.掌握平方差公式的结构特征,能运用公式进行简便运算;(重点)
2.会用几何图形说明公式的意义,体会数形结合的思想方法.(难点)
新课导入
复习回顾
1.平方差公式:
(1)符号表达式: .
(2)文字表达: .
2.判断下列算式能否运用平方差公式计算.
(1)(a+2)(a- 3); (2)(- m- n)(m- n);
(3)(2x+3y)(3x- 2y); (4)(4x- 3)(- 4x- 3).
(a+b)(a-b)=a2-b2
两数和与这两数差的积,等于它们的平方差
√
√
×
×
新课导入
情境引入
如图①,边长为a的大正方形中有一个边长为b的小正方形.将图①中的阴影部分拼成如图②所示的长方形.
你能表示剪拼前后的图形的面积关系吗?
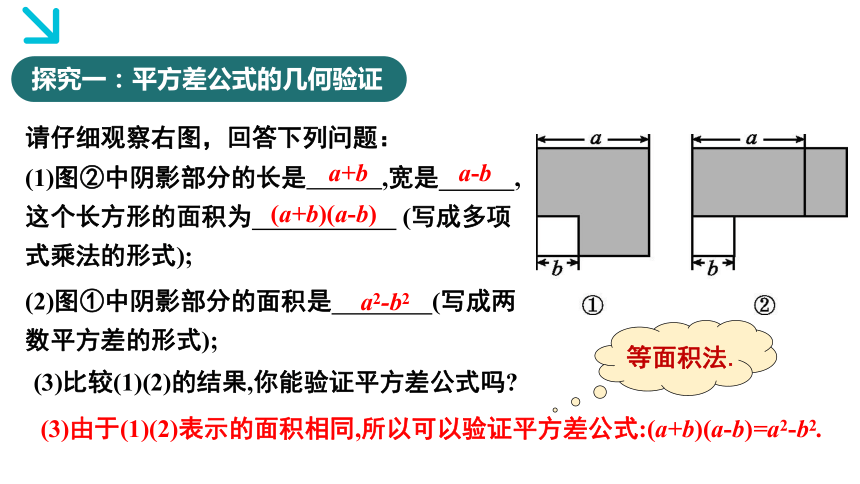
请仔细观察右图,回答下列问题:
(1)图②中阴影部分的长是 ,宽是 ,这个长方形的面积为 (写成多项式乘法的形式);
(2)图①中阴影部分的面积是 (写成两数平方差的形式);
新课讲授
探究一:平方差公式的几何验证
(a+b)(a-b)
a2-b2
a+b
a-b
(3)比较(1)(2)的结果,你能验证平方差公式吗
(3)由于(1)(2)表示的面积相同,所以可以验证平方差公式:(a+b)(a-b)=a2-b2.
等面积法.
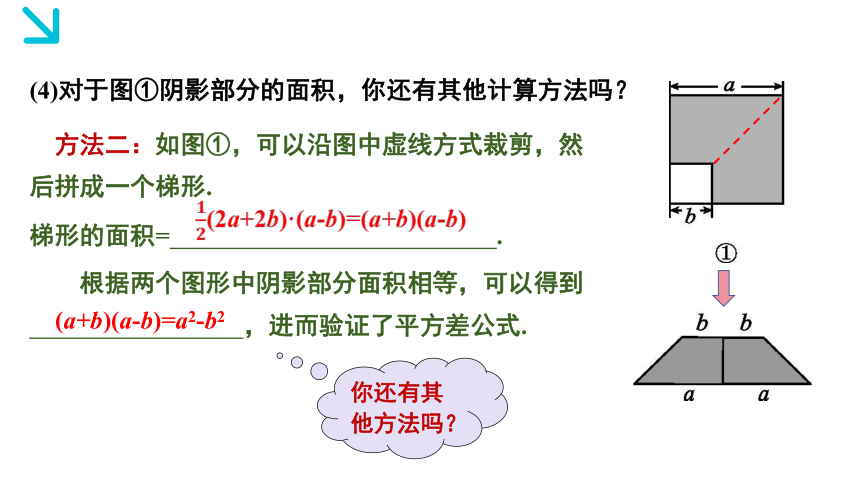
(4)对于图①阴影部分的面积,你还有其他计算方法吗?
根据两个图形中阴影部分面积相等,可以得到
,进而验证了平方差公式.
新课讲授
方法二:如图①,可以沿图中虚线方式裁剪,然后拼成一个梯形.
梯形的面积= .
(a+b)(a-b)=a2-b2
(2a+2b)·(a-b)=(a+b)(a-b)
你还有其他方法吗?
新课讲授
知识归纳
平方差公式的几何验证
运用不同方法分别表示两个不同图形的面积,利用面积相等,从而验证平方差公式.
新课讲授
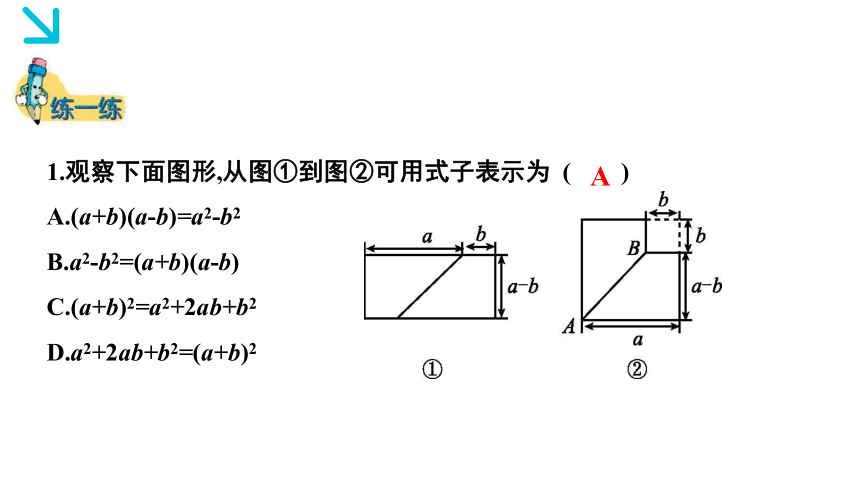
1.观察下面图形,从图①到图②可用式子表示为 ( )
A.(a+b)(a-b)=a2-b2
B.a2-b2=(a+b)(a-b)
C.(a+b)2=a2+2ab+b2
D.a2+2ab+b2=(a+b)2
A
(1)计算下列各组算式:
7×9= ,11×13= ,79×81= ,
8×8= ,12×12= ,80×80= .
观察·思考
新课讲授
63 143 6399
64 144 6400
用含字母a的式子表示这一规律,可写成 .
(a-1)(a+1)=a2-1
(2)观察上述算式及结果,你发现了什么规律?
(3)请用字母表示你发现的规律.
应用平方差公式(a+b)(a b)=a2 b2即可说明以上规律的正确性.
探究二:平方差公式的应用
新课讲授
2.利用平方差公式计算:
(1)103×97; (2)118×122.
解:(1)103×97
=(100+3)(100-3)
=1002-32
=9991.
(2)118×122
=(120-2)(120+2)
=1202-22
=14396.
新课讲授
知识归纳
利用平方差公式计算的方法:
运用平方差公式计算两数乘积时,关键是找到这两个数的平均数,再将原数与这个平均数进行比较,变成两数的和与差的积的形式.
新课讲授
3.计算:(1)a2(a+b)(a-b)+a2b2; (2)(2x-5)(2x+5)-2x(2x-3).
解:(1)a2(a+b)(a-b)+a2b2
=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4.
(2)(2x-5)(2x+5)-2x(2x-3)
=(2x)2-52-(4x2-6x)
=4x2-25-4x2+6x
=6x-25.
典例分析
例1: 用平方差公式进行计算:
(1)9.8×10.2; (2)20242-20162;
解:(1)原式=(10-0.2)×(10+0.2)
=102-0.22
=100-0.04
=99.96.
(2)20242-20162
=(2024+2016)(2024-2016)
=4040×8
=32320.
典例分析
例2: 计算:20242-2023×2025.
解:20242-2023×2025
=20242-(2024-1)(2024+1)
=20242-(20242-1)
=20242-20242+1
=1.
注意:不要漏掉括号.
典例分析
例3:小红家有一块L型的菜地,如图所示,要把L型的菜地按图中那样分成面积相等的两个梯形,种上不同的蔬菜,这两个梯形的上底都是a m,下底都是b m,高都是(b-a)m.请你帮小红家算一算这块L型菜地的面积共有多少,并求出当a=10,b=30时,L型菜地的总面积.
解:由题意得这块L型菜地的面积为2(a+b)·(b-a)=(b2-a2)m2.当a=10,b=30时,原式=302-102=800.因此,这块L型菜地的面积共有(b2-a2)m2.当a=10,b=30时,L型菜地的总面积为800 m2.
学以致用
2.将202×198变形正确的是 ( )
A.2002-4 B.2022-4
C.2002+2×200+4 D.2002-2×200+4
A
1.计算5a(2-5a)-(5a+1)(-5a+1)的结果是 ( )
A.1-10a+50a2 B.1-10a
C.10a-50a2-1 D.10a-1
D
学以致用
4.三个连续偶数,若中间一个偶数为n,则这三个连续偶数之积为( )
A.4n3-n B.n3-4n
C.8n2-8n D.8n3-2n
B
5.已知x2-y2=4,那么(x-y)2(x+y)2的结果是 ( )
A.4 B.8 C.16 D.32
C
3.如果用平方差公式计算(x-y+5)(x+y+5),则可将原式变形为 ( )
A.[(x-y)+5][(x+y)+5] B.[(x-y)+5][(x-y)-5]
C.[(x+5)-y][(x+5)+y] D.[x-(y+5)][x+(y+5)]
C
学以致用
6.填空:( ) (5a+1)=1-25a2.
7.计算:4x2(x-2y)(x+2y)+(4xy)2= .
8.若一个三角形的一条边长为(2a+4)cm,这条边上的高为(2a-4)cm,则这个三角形的面积为 cm2.
1-5a
4x4
(2a2-8)
9.若a+2b=-3,a2-4b2=24,则a-2b+1= .
10.观察下列各式:1×3=22-1,3×5=42-1,5×7=62-1,…,请你把发现的规律用含n(n为正整数)的等式表示出来:_____________ .
-7
(2n-1)(2n+1)=(2n)2-1
学以致用
11.利用平方差公式进行计算:
(1)1002×998; (2)-99.7×100.3.
解:(1)原式=(1000+2)×(1000-2)
=10002-4
=999996.
(2)原式=-(100-0.3)×(100+0.3)
=-1002+0.32
=-9999.91.
学以致用
(2)(a-2b)(2a-b)-(2a-b)(b+2a)=2a2-ab-4ab+2b2-[(2a)2-b2]=2a2-5ab+2b2-(4a2-b2)=2a2-5ab+2b2-4a2+b2=-2a2-5ab+3b2.
12.计算:
(1)3(a-2b)(); (2)(a-2b)(2a-b)-(2a-b)(b+2a).
学以致用
13.已知2a2+3a-6=0,求代数式3a(2a+1)-(2a+1)(2a-1)的值.
解:原式=6a2+3a-4a2+1
=2a2+3a+1.
因为2a2+3a-6=0,
所以2a2+3a=6,
所以原式=6+1=7.
课堂小结
乘法公式2
平方差公式的几何验证
利用几何图形,借助等面法可以验证平方差公式:(a+b)(a-b)=a2-b2.
平方差公式的应用
运用平方差公式计算两数乘积时,关键是找到这两个数的平均数,再将原数与这个平均数进行比较,变成两数的和与差的积的形式.
作业布置
习题1.3:2,6题.
1.3 乘法公式
第1章 整式的乘除
第2课时
北师大版(2024) 七年级 下册
学习目标
1.掌握平方差公式的结构特征,能运用公式进行简便运算;(重点)
2.会用几何图形说明公式的意义,体会数形结合的思想方法.(难点)
新课导入
复习回顾
1.平方差公式:
(1)符号表达式: .
(2)文字表达: .
2.判断下列算式能否运用平方差公式计算.
(1)(a+2)(a- 3); (2)(- m- n)(m- n);
(3)(2x+3y)(3x- 2y); (4)(4x- 3)(- 4x- 3).
(a+b)(a-b)=a2-b2
两数和与这两数差的积,等于它们的平方差
√
√
×
×
新课导入
情境引入
如图①,边长为a的大正方形中有一个边长为b的小正方形.将图①中的阴影部分拼成如图②所示的长方形.
你能表示剪拼前后的图形的面积关系吗?
请仔细观察右图,回答下列问题:
(1)图②中阴影部分的长是 ,宽是 ,这个长方形的面积为 (写成多项式乘法的形式);
(2)图①中阴影部分的面积是 (写成两数平方差的形式);
新课讲授
探究一:平方差公式的几何验证
(a+b)(a-b)
a2-b2
a+b
a-b
(3)比较(1)(2)的结果,你能验证平方差公式吗
(3)由于(1)(2)表示的面积相同,所以可以验证平方差公式:(a+b)(a-b)=a2-b2.
等面积法.
(4)对于图①阴影部分的面积,你还有其他计算方法吗?
根据两个图形中阴影部分面积相等,可以得到
,进而验证了平方差公式.
新课讲授
方法二:如图①,可以沿图中虚线方式裁剪,然后拼成一个梯形.
梯形的面积= .
(a+b)(a-b)=a2-b2
(2a+2b)·(a-b)=(a+b)(a-b)
你还有其他方法吗?
新课讲授
知识归纳
平方差公式的几何验证
运用不同方法分别表示两个不同图形的面积,利用面积相等,从而验证平方差公式.
新课讲授
1.观察下面图形,从图①到图②可用式子表示为 ( )
A.(a+b)(a-b)=a2-b2
B.a2-b2=(a+b)(a-b)
C.(a+b)2=a2+2ab+b2
D.a2+2ab+b2=(a+b)2
A
(1)计算下列各组算式:
7×9= ,11×13= ,79×81= ,
8×8= ,12×12= ,80×80= .
观察·思考
新课讲授
63 143 6399
64 144 6400
用含字母a的式子表示这一规律,可写成 .
(a-1)(a+1)=a2-1
(2)观察上述算式及结果,你发现了什么规律?
(3)请用字母表示你发现的规律.
应用平方差公式(a+b)(a b)=a2 b2即可说明以上规律的正确性.
探究二:平方差公式的应用
新课讲授
2.利用平方差公式计算:
(1)103×97; (2)118×122.
解:(1)103×97
=(100+3)(100-3)
=1002-32
=9991.
(2)118×122
=(120-2)(120+2)
=1202-22
=14396.
新课讲授
知识归纳
利用平方差公式计算的方法:
运用平方差公式计算两数乘积时,关键是找到这两个数的平均数,再将原数与这个平均数进行比较,变成两数的和与差的积的形式.
新课讲授
3.计算:(1)a2(a+b)(a-b)+a2b2; (2)(2x-5)(2x+5)-2x(2x-3).
解:(1)a2(a+b)(a-b)+a2b2
=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4.
(2)(2x-5)(2x+5)-2x(2x-3)
=(2x)2-52-(4x2-6x)
=4x2-25-4x2+6x
=6x-25.
典例分析
例1: 用平方差公式进行计算:
(1)9.8×10.2; (2)20242-20162;
解:(1)原式=(10-0.2)×(10+0.2)
=102-0.22
=100-0.04
=99.96.
(2)20242-20162
=(2024+2016)(2024-2016)
=4040×8
=32320.
典例分析
例2: 计算:20242-2023×2025.
解:20242-2023×2025
=20242-(2024-1)(2024+1)
=20242-(20242-1)
=20242-20242+1
=1.
注意:不要漏掉括号.
典例分析
例3:小红家有一块L型的菜地,如图所示,要把L型的菜地按图中那样分成面积相等的两个梯形,种上不同的蔬菜,这两个梯形的上底都是a m,下底都是b m,高都是(b-a)m.请你帮小红家算一算这块L型菜地的面积共有多少,并求出当a=10,b=30时,L型菜地的总面积.
解:由题意得这块L型菜地的面积为2(a+b)·(b-a)=(b2-a2)m2.当a=10,b=30时,原式=302-102=800.因此,这块L型菜地的面积共有(b2-a2)m2.当a=10,b=30时,L型菜地的总面积为800 m2.
学以致用
2.将202×198变形正确的是 ( )
A.2002-4 B.2022-4
C.2002+2×200+4 D.2002-2×200+4
A
1.计算5a(2-5a)-(5a+1)(-5a+1)的结果是 ( )
A.1-10a+50a2 B.1-10a
C.10a-50a2-1 D.10a-1
D
学以致用
4.三个连续偶数,若中间一个偶数为n,则这三个连续偶数之积为( )
A.4n3-n B.n3-4n
C.8n2-8n D.8n3-2n
B
5.已知x2-y2=4,那么(x-y)2(x+y)2的结果是 ( )
A.4 B.8 C.16 D.32
C
3.如果用平方差公式计算(x-y+5)(x+y+5),则可将原式变形为 ( )
A.[(x-y)+5][(x+y)+5] B.[(x-y)+5][(x-y)-5]
C.[(x+5)-y][(x+5)+y] D.[x-(y+5)][x+(y+5)]
C
学以致用
6.填空:( ) (5a+1)=1-25a2.
7.计算:4x2(x-2y)(x+2y)+(4xy)2= .
8.若一个三角形的一条边长为(2a+4)cm,这条边上的高为(2a-4)cm,则这个三角形的面积为 cm2.
1-5a
4x4
(2a2-8)
9.若a+2b=-3,a2-4b2=24,则a-2b+1= .
10.观察下列各式:1×3=22-1,3×5=42-1,5×7=62-1,…,请你把发现的规律用含n(n为正整数)的等式表示出来:_____________ .
-7
(2n-1)(2n+1)=(2n)2-1
学以致用
11.利用平方差公式进行计算:
(1)1002×998; (2)-99.7×100.3.
解:(1)原式=(1000+2)×(1000-2)
=10002-4
=999996.
(2)原式=-(100-0.3)×(100+0.3)
=-1002+0.32
=-9999.91.
学以致用
(2)(a-2b)(2a-b)-(2a-b)(b+2a)=2a2-ab-4ab+2b2-[(2a)2-b2]=2a2-5ab+2b2-(4a2-b2)=2a2-5ab+2b2-4a2+b2=-2a2-5ab+3b2.
12.计算:
(1)3(a-2b)(); (2)(a-2b)(2a-b)-(2a-b)(b+2a).
学以致用
13.已知2a2+3a-6=0,求代数式3a(2a+1)-(2a+1)(2a-1)的值.
解:原式=6a2+3a-4a2+1
=2a2+3a+1.
因为2a2+3a-6=0,
所以2a2+3a=6,
所以原式=6+1=7.
课堂小结
乘法公式2
平方差公式的几何验证
利用几何图形,借助等面法可以验证平方差公式:(a+b)(a-b)=a2-b2.
平方差公式的应用
运用平方差公式计算两数乘积时,关键是找到这两个数的平均数,再将原数与这个平均数进行比较,变成两数的和与差的积的形式.
作业布置
习题1.3:2,6题.
同课章节目录
