课题:18.1勾股定理(1)
文档属性
| 名称 | 课题:18.1勾股定理(1) |  | |
| 格式 | rar | ||
| 文件大小 | 89.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-11-21 15:09:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
课题:18.1勾股定理(1) 班级: 姓名: .
知识技能 1.了解勾股定理的由来,经历探索勾股定理的过程.2.理解并能用不同的方法证明勾股定理,并能简单的运用.3. 提高推理意识与探究习惯,感受我国古代数学的伟大成就.
重点难点 重点:勾股定理及及其应用.
难点:用面积法(拼图法)证明勾股定理.
导学过程
预习导航 阅读课本第64页至66页的部分,完成以下问题.
活动一 【情景引入】1.在我校实验楼与教学楼一楼之间的连廊上,有一幅如上图所示的图案,这也是2002年8月在北京举行的国际数学家大会的会标。这幅美丽而神秘的图案有什么秘密呢?2.毕达哥拉斯在地板上的发现:3、一般的直角三角形是否也具有这种关系呢?根据上图展开探究。【归纳猜想】直角三角形三边长度之间存在什么关系? .【证明】我们还是选择刚才认识的弦图来证明.请用准备好的4个直角三角形摆出弦图,并用两种方式求出弦图的面积(独立思考后可组内交流)。【得出结论】 .变式: .定理: .
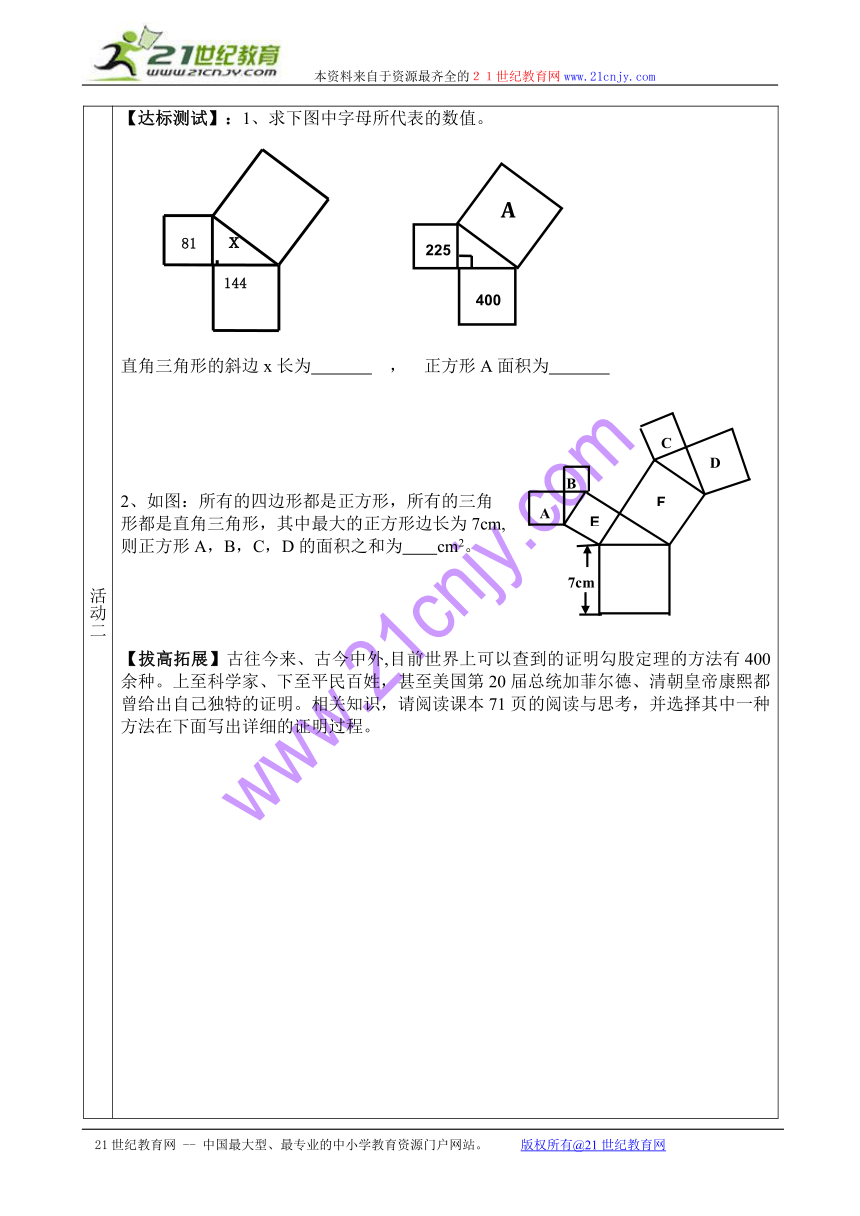
活动二 【达标测试】:1、求下图中字母所代表的数值。直角三角形的斜边x长为 , 正方形A面积为 2、如图:所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为7cm,则正方形A,B,C,D的面积之和为 cm2。【拔高拓展】古往今来、古今中外,目前世界上可以查到的证明勾股定理的方法有400余种。上至科学家、下至平民百姓,甚至美国第20届总统加菲尔德、清朝皇帝康熙都曾给出自己独特的证明。相关知识,请阅读课本71页的阅读与思考,并选择其中一种方法在下面写出详细的证明过程。
【作业设计】1. 右图阴影部分是一个正方形,求此正方形的面积.2.课本第69页习题18.1第1题,70页第2题.
A
B
C
A
B
C
a
b
c
81
144
x
225
400
A
A
B
C
D
7cm
F
E
12cm
13cm
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
课题:18.1勾股定理(1) 班级: 姓名: .
知识技能 1.了解勾股定理的由来,经历探索勾股定理的过程.2.理解并能用不同的方法证明勾股定理,并能简单的运用.3. 提高推理意识与探究习惯,感受我国古代数学的伟大成就.
重点难点 重点:勾股定理及及其应用.
难点:用面积法(拼图法)证明勾股定理.
导学过程
预习导航 阅读课本第64页至66页的部分,完成以下问题.
活动一 【情景引入】1.在我校实验楼与教学楼一楼之间的连廊上,有一幅如上图所示的图案,这也是2002年8月在北京举行的国际数学家大会的会标。这幅美丽而神秘的图案有什么秘密呢?2.毕达哥拉斯在地板上的发现:3、一般的直角三角形是否也具有这种关系呢?根据上图展开探究。【归纳猜想】直角三角形三边长度之间存在什么关系? .【证明】我们还是选择刚才认识的弦图来证明.请用准备好的4个直角三角形摆出弦图,并用两种方式求出弦图的面积(独立思考后可组内交流)。【得出结论】 .变式: .定理: .
活动二 【达标测试】:1、求下图中字母所代表的数值。直角三角形的斜边x长为 , 正方形A面积为 2、如图:所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为7cm,则正方形A,B,C,D的面积之和为 cm2。【拔高拓展】古往今来、古今中外,目前世界上可以查到的证明勾股定理的方法有400余种。上至科学家、下至平民百姓,甚至美国第20届总统加菲尔德、清朝皇帝康熙都曾给出自己独特的证明。相关知识,请阅读课本71页的阅读与思考,并选择其中一种方法在下面写出详细的证明过程。
【作业设计】1. 右图阴影部分是一个正方形,求此正方形的面积.2.课本第69页习题18.1第1题,70页第2题.
A
B
C
A
B
C
a
b
c
81
144
x
225
400
A
A
B
C
D
7cm
F
E
12cm
13cm
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
