沪科版数学九年级上册第21章二次函数与反比例函数专项梳理练习专题(含答案)
文档属性
| 名称 | 沪科版数学九年级上册第21章二次函数与反比例函数专项梳理练习专题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 214.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 23:09:11 | ||
图片预览


文档简介
第21章 专项梳理练习专题
专题1 二次函数的有关概念
1.下列函数表达式中,一定为二次函数的是 ( )
A. y=3x--1
2.已知函数 为二次函数,则m的取值范围是 ( )
A. m≠0 B. m≠-1 C. m≠0且m≠-1 D. m=-1
3.已知二次函数则其二次项系数a,一次项系数b,常数项c分别是 ( )
4.已知函数 .
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,则m的值应怎样
专题 2 二次函数的图象与性质
1.抛物线的顶点坐标为 ( )
A.(1,3) B.(1,-3) C.(-1,-3) D.(-1,3)
2.若抛物线的顶点在第一象限,则m的取值范围为 ( )
A. m>1 B. m>0 C. m>-1 D.-13.在二次函数 的图象上有两点(-1,y ),(1,y ),,则 y 与y 的大小关系是 ( )
D.不能确定
4.对于抛物线 ,有下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小,其中正确结论的个数为 ( )
A.1 B.2 C.3 D.4
5.抛物线 的顶点在x轴上,则m等于 ( )
A.-16 B. -4 C.8 D.16
6.已知二次函数 ,当x>1时,y随x的增大而增大,则m的取值范围是 ( )
A. m=-1 B. m=3 C.m≤-1 D.m≥-1
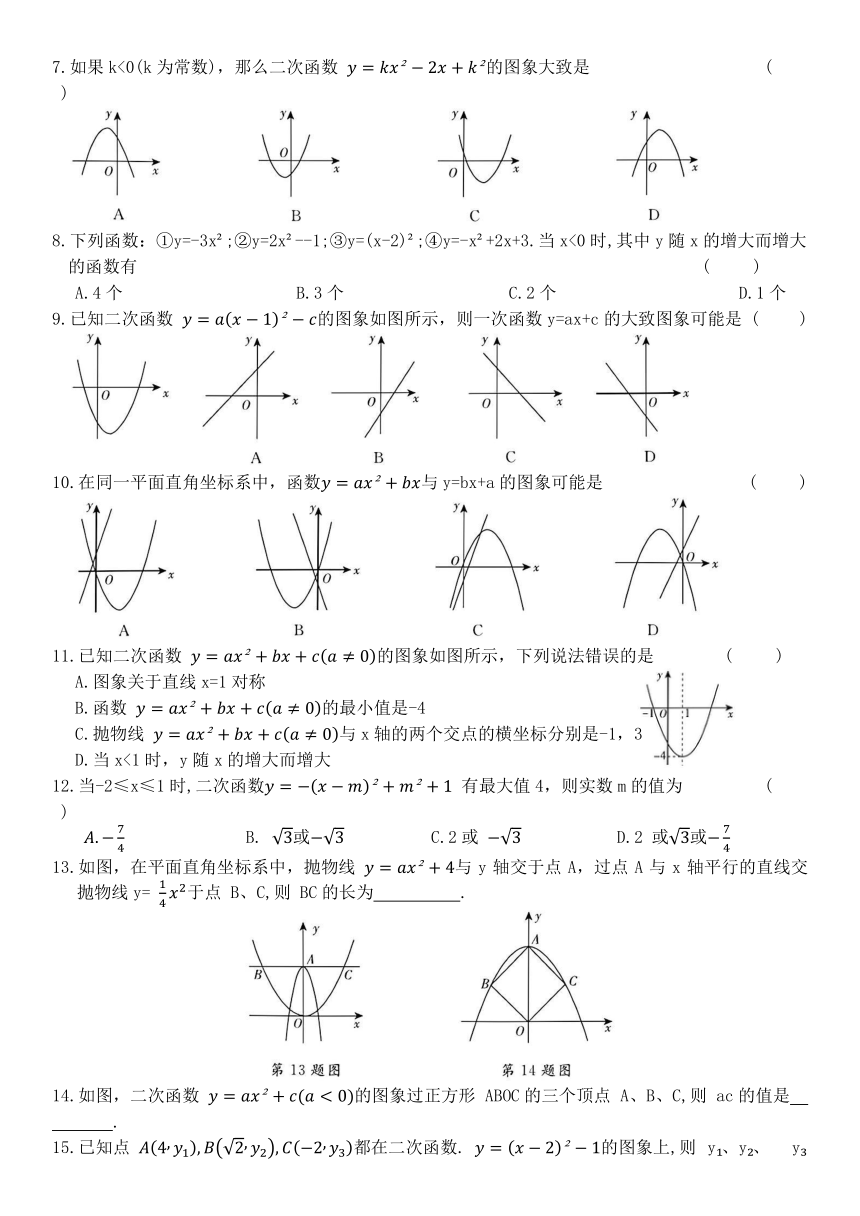
7.如果k<0(k为常数),那么二次函数 的图象大致是 ( )
8.下列函数:①y=-3x ;②y=2x --1;③y=(x-2) ;④y=-x +2x+3.当x<0时,其中y随x的增大而增大的函数有 ( )
A.4个 B.3个 C.2个 D.1个
9.已知二次函数 的图象如图所示,则一次函数y=ax+c的大致图象可能是 ( )
10.在同一平面直角坐标系中,函数与y=bx+a的图象可能是 ( )
11.已知二次函数 的图象如图所示,下列说法错误的是 ( )
A.图象关于直线x=1对称
B.函数 的最小值是-4
C.抛物线 与x轴的两个交点的横坐标分别是-1,3
D.当x<1时,y随x的增大而增大
12.当-2≤x≤1时,二次函数 有最大值4,则实数m的值为 ( )
B. 或 C.2或 D.2 或或
13.如图,在平面直角坐标系中,抛物线 与y轴交于点A,过点A与x轴平行的直线交抛物线y= 于点 B、C,则 BC的长为 .
14.如图,二次函数 的图象过正方形 ABOC的三个顶点 A、B、C,则 ac的值是 .
15.已知点 都在二次函数. 的图象上,则 y 、y 、 y 的大小关系是 .
16.如图,已知抛物线 与x轴的一个交点为A(3,0),与y轴的交点B(0,3),其顶点为C,对称轴为直线x=1
(1)求该抛物线的顶点 C 的坐标;
(2)已知点 M为y 轴上的一个动点,当△ABM为等腰三角形时,求点 M 的坐标.
17.已知抛物线
(1)在给定的坐标轴中画出该抛物线;
(2)用配方法求出该抛物线的对称轴和顶点坐标;
(3)设抛物线与x轴的两个交点为A、B(点A 在点B 的左侧),与y轴的交点为C,请根据图象直接写出A、B、C三点的坐标;
(4)当x取何值时,抛物线在x轴的上方
专题3 二次函数的图象与字母取值
1.如图,二次函数 的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是 ( )
A. abc<0 B.2a+b<0 C. a-b+c<0
2.已知抛物线 的图象如图所示,则|a-b+c|+|2a+b|= ( )
A. a+b B. a-2b C. a-b D.3a
3.如图是二次函数 图象的一部分,其对称轴是x=-1,且过点(-3,0),下列说法:
①abc<0②2a-b=0 ③4a+2b+c<0 ④若 是抛物线上两点,则. 其中说法正确的是( )
A.①② B.②③ C.①②④ D.②③④
4.已知二次函数 的图象如图所示,对称轴是直线x=-1,下列结论:①abc<0;②2a+b=0;③a-b+c>0;④4a-2b+c<0.其中正确的是 ( )
A.①② B.只有① C.③④ D.①④
5.已知二次函数 的图象如图所示,有下列5个结论:①abc<0;②b0;④2c<3b;⑤a+b其中正确结论的序号有 .
专题4 二次函数解析式的确定
1.已知二次函数的图象经过点(-1,-5),(0,-4)和(1,1),则这个二次函数的表达式为 ( )
2.顶点为(6,0),开口向下,开口的大小与函数 的图象相同的抛物线所对应的函数表达式是 ( )
3.若二次函数的图象的顶点坐标为(2,-1),抛物线过点(0,3),则二次函数的解析式是 ( )
4.已知抛物线 的对称轴为x=3,则该抛物线的解析式为 ( )
5.抛物线 上部分点的横坐标x,纵坐标y的对应值如下表:
x —2 —1 0 1 2
y 0 4 6 6 4
从上表可知,下列说法正确的个数是: ( )
①抛物线与x轴的一个交点为(-2,0) ②抛物线与y轴的交点为(0,6) ③抛物线的对称轴是: x=1
④在对称轴左侧y随x 增大而增大
A.1 B.2 C.3 D.4
6.若抛物线 的经过坐标原点,则该抛物线的解析式为 .
7.若函数 的图象经过坐标原点,且最大值为8,形状与抛物线 相同,则此函数表达式为 .
8.已知二次函数 的图象经过点A(0.4)和B(1,-2).
(1)求此抛物线的解析式;
(2)求此抛物线的对称轴和顶点坐标;
(3)设抛物线的顶点为 C,试求△CAO的面积.
第21章 专项梳理练习专题
专题1 二次函数的有关概念
1. C 2. C 3. D
4.解:(1)∵要使此函数为一次函数,
∴必须有: 且m-1≠0,
解得: 且m≠1,
故当m=0时,这个函数是一次函数,即m的值为0;
(2)∵要使此函数为二次函数,
∴必须有
解得:
∴当ím ≠0,m ≠1时,这个函数是二次函数.
专题 2 二次函数的图象与性质
1. D 2. B 3. A 4. C 5. D 6. D 7. A 8. C9. A 10. C 11. D 12. C
13.8 14.—2 15. y >y >y
16.解:(1)∵抛物线的对称轴为直线x=1,∴h=1,
∵该抛物线经过A(3,0),B(0,3),
解得:
∴抛物线的解析式为 故抛物线的顶点 C 的坐标为(1,4);
(2)由题意知:OA=3,OB=3,由勾股定理得:
当△ABM为等腰三角形时,
①若以AB为底,∵OA=OB=3,∴此时点O即为所求的点 M,故点 M 的坐标为(0,0);
②若以 AB 为腰,以点 B 为圆心,以 3 /2长为半径画弧,交y轴于两点,
此时两点坐标为
以点 A 为圆心,以3 /2长为半径画弧,交y轴于点(0,-3),
综合上述,当△ABM为等腰三角形时,点M 的坐标分别为(0,0)、
17.解:(1)画函数图象如图所示:
∴抛物线的对称轴为直线x=2,顶点坐标为(2,1);
(3)由图象可知:A(1,0),B(3,0),C(0,—3);
(4)当 时,抛物线在x轴的上方.
专题 3 二次函数的图象与字母取值
1. D 2. D 3. C 4. D 5.①③④
专题 4 二次函数解析式的确定
1. D 2. D 3. C 4. B 5. C
或
8.解:(1)把 A(0,4)和 代入
bx+c得: 解得:
∴此抛物线的解析式为
∴此抛物线的对称轴为直线. 顶点坐标为
(3)由(2)知:顶点(
∵点A(0,4) 即 的面积为 2.
专题1 二次函数的有关概念
1.下列函数表达式中,一定为二次函数的是 ( )
A. y=3x--1
2.已知函数 为二次函数,则m的取值范围是 ( )
A. m≠0 B. m≠-1 C. m≠0且m≠-1 D. m=-1
3.已知二次函数则其二次项系数a,一次项系数b,常数项c分别是 ( )
4.已知函数 .
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,则m的值应怎样
专题 2 二次函数的图象与性质
1.抛物线的顶点坐标为 ( )
A.(1,3) B.(1,-3) C.(-1,-3) D.(-1,3)
2.若抛物线的顶点在第一象限,则m的取值范围为 ( )
A. m>1 B. m>0 C. m>-1 D.-1
D.不能确定
4.对于抛物线 ,有下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小,其中正确结论的个数为 ( )
A.1 B.2 C.3 D.4
5.抛物线 的顶点在x轴上,则m等于 ( )
A.-16 B. -4 C.8 D.16
6.已知二次函数 ,当x>1时,y随x的增大而增大,则m的取值范围是 ( )
A. m=-1 B. m=3 C.m≤-1 D.m≥-1
7.如果k<0(k为常数),那么二次函数 的图象大致是 ( )
8.下列函数:①y=-3x ;②y=2x --1;③y=(x-2) ;④y=-x +2x+3.当x<0时,其中y随x的增大而增大的函数有 ( )
A.4个 B.3个 C.2个 D.1个
9.已知二次函数 的图象如图所示,则一次函数y=ax+c的大致图象可能是 ( )
10.在同一平面直角坐标系中,函数与y=bx+a的图象可能是 ( )
11.已知二次函数 的图象如图所示,下列说法错误的是 ( )
A.图象关于直线x=1对称
B.函数 的最小值是-4
C.抛物线 与x轴的两个交点的横坐标分别是-1,3
D.当x<1时,y随x的增大而增大
12.当-2≤x≤1时,二次函数 有最大值4,则实数m的值为 ( )
B. 或 C.2或 D.2 或或
13.如图,在平面直角坐标系中,抛物线 与y轴交于点A,过点A与x轴平行的直线交抛物线y= 于点 B、C,则 BC的长为 .
14.如图,二次函数 的图象过正方形 ABOC的三个顶点 A、B、C,则 ac的值是 .
15.已知点 都在二次函数. 的图象上,则 y 、y 、 y 的大小关系是 .
16.如图,已知抛物线 与x轴的一个交点为A(3,0),与y轴的交点B(0,3),其顶点为C,对称轴为直线x=1
(1)求该抛物线的顶点 C 的坐标;
(2)已知点 M为y 轴上的一个动点,当△ABM为等腰三角形时,求点 M 的坐标.
17.已知抛物线
(1)在给定的坐标轴中画出该抛物线;
(2)用配方法求出该抛物线的对称轴和顶点坐标;
(3)设抛物线与x轴的两个交点为A、B(点A 在点B 的左侧),与y轴的交点为C,请根据图象直接写出A、B、C三点的坐标;
(4)当x取何值时,抛物线在x轴的上方
专题3 二次函数的图象与字母取值
1.如图,二次函数 的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是 ( )
A. abc<0 B.2a+b<0 C. a-b+c<0
2.已知抛物线 的图象如图所示,则|a-b+c|+|2a+b|= ( )
A. a+b B. a-2b C. a-b D.3a
3.如图是二次函数 图象的一部分,其对称轴是x=-1,且过点(-3,0),下列说法:
①abc<0②2a-b=0 ③4a+2b+c<0 ④若 是抛物线上两点,则. 其中说法正确的是( )
A.①② B.②③ C.①②④ D.②③④
4.已知二次函数 的图象如图所示,对称轴是直线x=-1,下列结论:①abc<0;②2a+b=0;③a-b+c>0;④4a-2b+c<0.其中正确的是 ( )
A.①② B.只有① C.③④ D.①④
5.已知二次函数 的图象如图所示,有下列5个结论:①abc<0;②b
专题4 二次函数解析式的确定
1.已知二次函数的图象经过点(-1,-5),(0,-4)和(1,1),则这个二次函数的表达式为 ( )
2.顶点为(6,0),开口向下,开口的大小与函数 的图象相同的抛物线所对应的函数表达式是 ( )
3.若二次函数的图象的顶点坐标为(2,-1),抛物线过点(0,3),则二次函数的解析式是 ( )
4.已知抛物线 的对称轴为x=3,则该抛物线的解析式为 ( )
5.抛物线 上部分点的横坐标x,纵坐标y的对应值如下表:
x —2 —1 0 1 2
y 0 4 6 6 4
从上表可知,下列说法正确的个数是: ( )
①抛物线与x轴的一个交点为(-2,0) ②抛物线与y轴的交点为(0,6) ③抛物线的对称轴是: x=1
④在对称轴左侧y随x 增大而增大
A.1 B.2 C.3 D.4
6.若抛物线 的经过坐标原点,则该抛物线的解析式为 .
7.若函数 的图象经过坐标原点,且最大值为8,形状与抛物线 相同,则此函数表达式为 .
8.已知二次函数 的图象经过点A(0.4)和B(1,-2).
(1)求此抛物线的解析式;
(2)求此抛物线的对称轴和顶点坐标;
(3)设抛物线的顶点为 C,试求△CAO的面积.
第21章 专项梳理练习专题
专题1 二次函数的有关概念
1. C 2. C 3. D
4.解:(1)∵要使此函数为一次函数,
∴必须有: 且m-1≠0,
解得: 且m≠1,
故当m=0时,这个函数是一次函数,即m的值为0;
(2)∵要使此函数为二次函数,
∴必须有
解得:
∴当ím ≠0,m ≠1时,这个函数是二次函数.
专题 2 二次函数的图象与性质
1. D 2. B 3. A 4. C 5. D 6. D 7. A 8. C9. A 10. C 11. D 12. C
13.8 14.—2 15. y >y >y
16.解:(1)∵抛物线的对称轴为直线x=1,∴h=1,
∵该抛物线经过A(3,0),B(0,3),
解得:
∴抛物线的解析式为 故抛物线的顶点 C 的坐标为(1,4);
(2)由题意知:OA=3,OB=3,由勾股定理得:
当△ABM为等腰三角形时,
①若以AB为底,∵OA=OB=3,∴此时点O即为所求的点 M,故点 M 的坐标为(0,0);
②若以 AB 为腰,以点 B 为圆心,以 3 /2长为半径画弧,交y轴于两点,
此时两点坐标为
以点 A 为圆心,以3 /2长为半径画弧,交y轴于点(0,-3),
综合上述,当△ABM为等腰三角形时,点M 的坐标分别为(0,0)、
17.解:(1)画函数图象如图所示:
∴抛物线的对称轴为直线x=2,顶点坐标为(2,1);
(3)由图象可知:A(1,0),B(3,0),C(0,—3);
(4)当 时,抛物线在x轴的上方.
专题 3 二次函数的图象与字母取值
1. D 2. D 3. C 4. D 5.①③④
专题 4 二次函数解析式的确定
1. D 2. D 3. C 4. B 5. C
或
8.解:(1)把 A(0,4)和 代入
bx+c得: 解得:
∴此抛物线的解析式为
∴此抛物线的对称轴为直线. 顶点坐标为
(3)由(2)知:顶点(
∵点A(0,4) 即 的面积为 2.
