江苏省江阴市南菁高级中学2016届高三数学第一次模拟考试(无答案)
文档属性
| 名称 | 江苏省江阴市南菁高级中学2016届高三数学第一次模拟考试(无答案) | 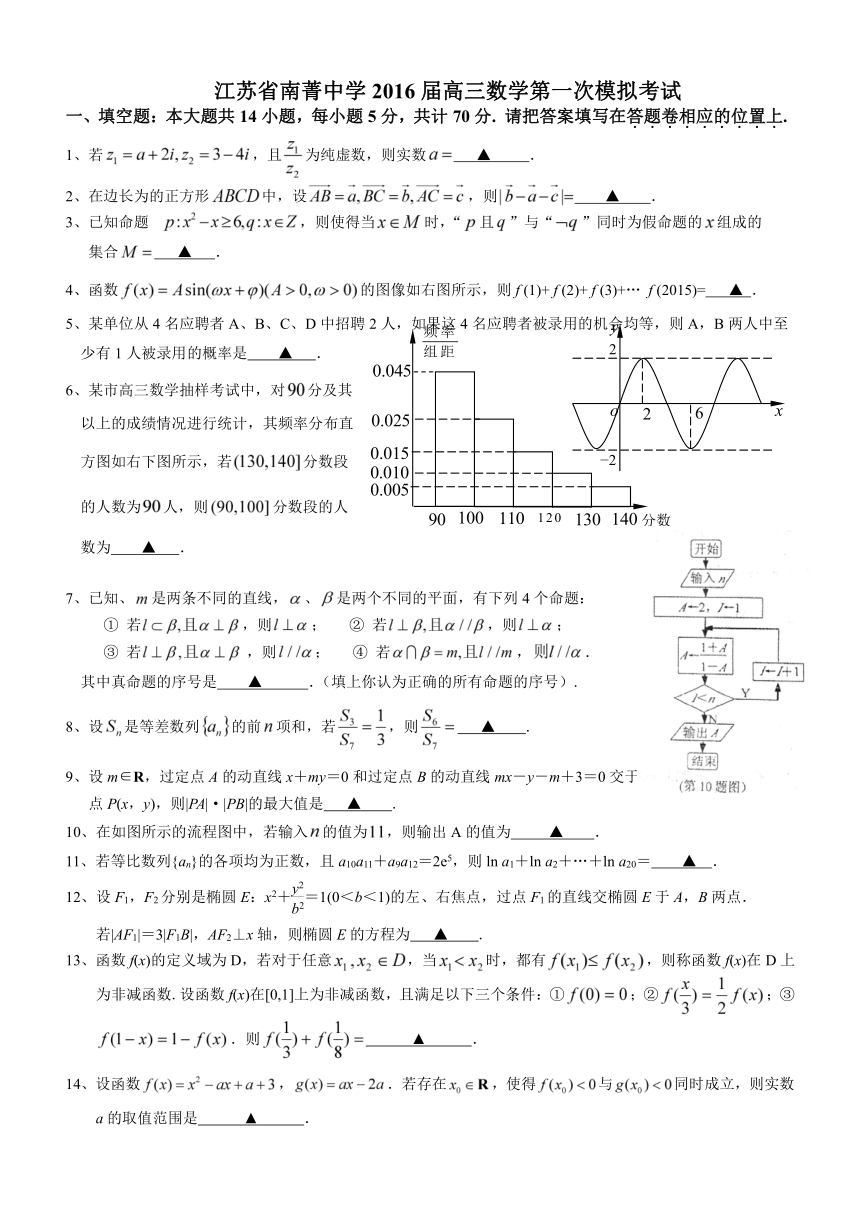 | |
| 格式 | zip | ||
| 文件大小 | 103.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-21 16:01:27 | ||
图片预览

文档简介
江苏省南菁中学2016届高三数学第一次模拟考试
一、填空题:本大题共14小题,每小题5分,共计70分. 请把答案填写在答题卷相应的位置上.
1、若,且为纯虚数,则实数 ▲ .
2、在边长为的正方形中,设,则 ▲ .
3、已知命题,则使得当时,“且”与“”同时为假命题的组成的
集合 ▲ .
4、函数的图像如右图所示,则f (1)+ f (2)+ f (3)+… f (2015)= ▲ .
5、某单位从4名应聘者A、B、C、D中招聘2人,如果这4名应聘者被录用的机会均等,则A,B两人中至
少有1人被录用的概率是 ▲ .
6、某市高三数学抽样考试中,对分及其
以上的成绩情况进行统计,其频率分布直
方图如右下图所示,若分数段
的人数为人,则分数段的人
数为 ▲ .
7、已知、是两条不同的直线,、是两个不同的平面,有下列4个命题:
① 若,则; ② 若,则;
③ 若,则; ④ 若,.
其中真命题的序号是 ▲ .(填上你认为正确的所有命题的序号).
8、设是等差数列的前项和,若,则 ▲ .
9、设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于
点P(x,y),则|PA|·|PB|的最大值是 ▲ .
10、在如图所示的流程图中,若输入的值为,则输出A的值为 ▲ .
11、若等比数列{an}的各项均为正数,且a10a11+a9a12=2e5,则ln a1+ln a2+…+ln a20= ▲ .
12、设F1,F2分别是椭圆E:x2+=1(0<b<1)的左、右焦点,过点F1的直线交椭圆E于A,B两点.
若|AF1|=3|F1B|,AF2⊥x轴,则椭圆E的方程为 ▲ .
13、函数f(x)的定义域为D,若对于任意,当时,都有,则称函数f(x)在D上为非减函数.设函数f(x)在[0,1]上为非减函数,且满足以下三个条件:①;②;③.则 ▲ .
14、设函数,.若存在,使得与同时成立,则实数a的取值范围是 ▲ .
二、解答题:
15、(本小题满分14分)设函数的图象相邻两条对称轴之间的距离为,
函数为偶函数.
(1) 求的解析式;
(2) 若为锐角,,求的值.
16、(本小题满分14分)在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,
AA1=AC=BC=1,A1B=.
(1) 求证:平面A1BC⊥平面ACC1A1;
(2) 如果D为AB的中点,求证:BC1//平面A1CD.
17、(本小题满分14分)某工厂接到一标识制作订单,标识如图所示,分为两部分,“T型”部分为宽为10cm 的两个矩形相接而成,圆面部分的圆周是A,C,D,F的外接圆.要求如下:① “T型”部分的面积不得小于800cm2;②两矩形的长均大于外接圆半径.为了节约成本,设计时应尽量减小圆面的面积.此工厂的设计师,凭直觉认为当“型”部分的面积取800cm2且两矩形的长相等时,成本是最低的.你同意他的观点吗?试通过计算,说说你的理由.
18、(本小题满分16分)已知椭圆C:x2+2y2=4.
(1) 求椭圆C的离心率;
(2) 设O为原点,若点A在椭圆C上,点B在直线y=2上,且OA⊥OB,试判断直线AB与圆x2+y2=2
的位置关系,并证明你的结论.
19、(本小题满分16分)已知函数在时取得极小值.
(1) 求实数的值;
(2) 是否存在区间,使得在该区间上的值域为?若存在,求出,的值;若不存在,说明理由.
20、(本小题满分16分)已知数列{an}中,a2=a(a为非零常数),其前n项和Sn满足:Sn=(nN*).
(1)求数列{an}的通项公式;
(2)若a=2,且,求m、n的值;
(3)是否存在实数a、b,使得对任意正整数p,数列{an}中满足的最大项恰为第3p-2项 若存在,分别求出a与b的取值范围;若不存在,请说明理由.
分数
2
2
一、填空题:本大题共14小题,每小题5分,共计70分. 请把答案填写在答题卷相应的位置上.
1、若,且为纯虚数,则实数 ▲ .
2、在边长为的正方形中,设,则 ▲ .
3、已知命题,则使得当时,“且”与“”同时为假命题的组成的
集合 ▲ .
4、函数的图像如右图所示,则f (1)+ f (2)+ f (3)+… f (2015)= ▲ .
5、某单位从4名应聘者A、B、C、D中招聘2人,如果这4名应聘者被录用的机会均等,则A,B两人中至
少有1人被录用的概率是 ▲ .
6、某市高三数学抽样考试中,对分及其
以上的成绩情况进行统计,其频率分布直
方图如右下图所示,若分数段
的人数为人,则分数段的人
数为 ▲ .
7、已知、是两条不同的直线,、是两个不同的平面,有下列4个命题:
① 若,则; ② 若,则;
③ 若,则; ④ 若,.
其中真命题的序号是 ▲ .(填上你认为正确的所有命题的序号).
8、设是等差数列的前项和,若,则 ▲ .
9、设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于
点P(x,y),则|PA|·|PB|的最大值是 ▲ .
10、在如图所示的流程图中,若输入的值为,则输出A的值为 ▲ .
11、若等比数列{an}的各项均为正数,且a10a11+a9a12=2e5,则ln a1+ln a2+…+ln a20= ▲ .
12、设F1,F2分别是椭圆E:x2+=1(0<b<1)的左、右焦点,过点F1的直线交椭圆E于A,B两点.
若|AF1|=3|F1B|,AF2⊥x轴,则椭圆E的方程为 ▲ .
13、函数f(x)的定义域为D,若对于任意,当时,都有,则称函数f(x)在D上为非减函数.设函数f(x)在[0,1]上为非减函数,且满足以下三个条件:①;②;③.则 ▲ .
14、设函数,.若存在,使得与同时成立,则实数a的取值范围是 ▲ .
二、解答题:
15、(本小题满分14分)设函数的图象相邻两条对称轴之间的距离为,
函数为偶函数.
(1) 求的解析式;
(2) 若为锐角,,求的值.
16、(本小题满分14分)在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,
AA1=AC=BC=1,A1B=.
(1) 求证:平面A1BC⊥平面ACC1A1;
(2) 如果D为AB的中点,求证:BC1//平面A1CD.
17、(本小题满分14分)某工厂接到一标识制作订单,标识如图所示,分为两部分,“T型”部分为宽为10cm 的两个矩形相接而成,圆面部分的圆周是A,C,D,F的外接圆.要求如下:① “T型”部分的面积不得小于800cm2;②两矩形的长均大于外接圆半径.为了节约成本,设计时应尽量减小圆面的面积.此工厂的设计师,凭直觉认为当“型”部分的面积取800cm2且两矩形的长相等时,成本是最低的.你同意他的观点吗?试通过计算,说说你的理由.
18、(本小题满分16分)已知椭圆C:x2+2y2=4.
(1) 求椭圆C的离心率;
(2) 设O为原点,若点A在椭圆C上,点B在直线y=2上,且OA⊥OB,试判断直线AB与圆x2+y2=2
的位置关系,并证明你的结论.
19、(本小题满分16分)已知函数在时取得极小值.
(1) 求实数的值;
(2) 是否存在区间,使得在该区间上的值域为?若存在,求出,的值;若不存在,说明理由.
20、(本小题满分16分)已知数列{an}中,a2=a(a为非零常数),其前n项和Sn满足:Sn=(nN*).
(1)求数列{an}的通项公式;
(2)若a=2,且,求m、n的值;
(3)是否存在实数a、b,使得对任意正整数p,数列{an}中满足的最大项恰为第3p-2项 若存在,分别求出a与b的取值范围;若不存在,请说明理由.
分数
2
2
同课章节目录
