2.2双曲线及其标准方程说课课件
图片预览




文档简介
课件23张PPT。
2.2.1双曲线及其标准方程輔仁存義新课标
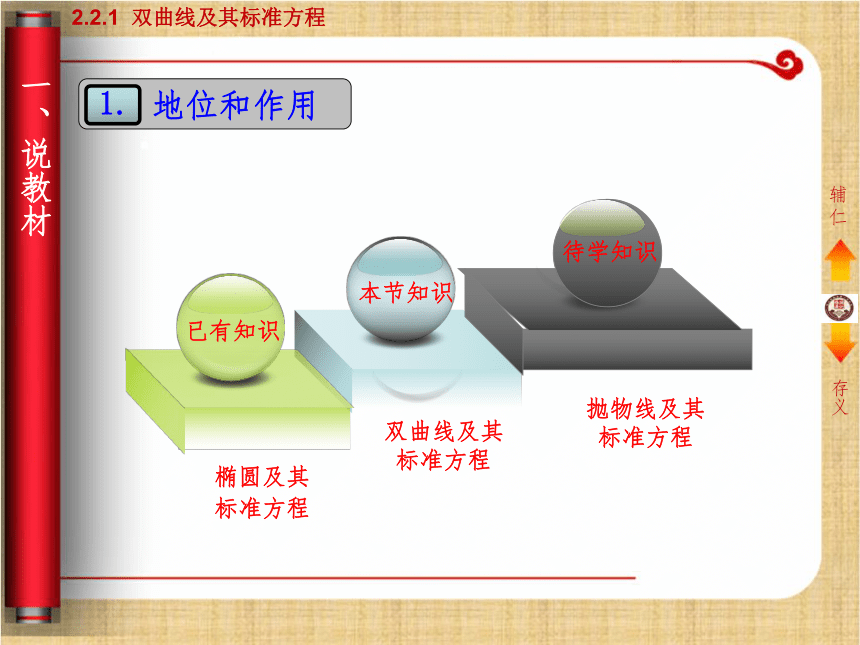
教材一、说教材 地位和作用1.辅仁存义2.2.1 双曲线及其标准方程叙永一中 张金虎理解双曲线的定义,掌握双曲线标准方程通过双曲线定义及标准方程的探究,让学生进一步体验类比、数形结合等思想方法的运用,提高学生观察问题、探究问题、归纳问题的能力.
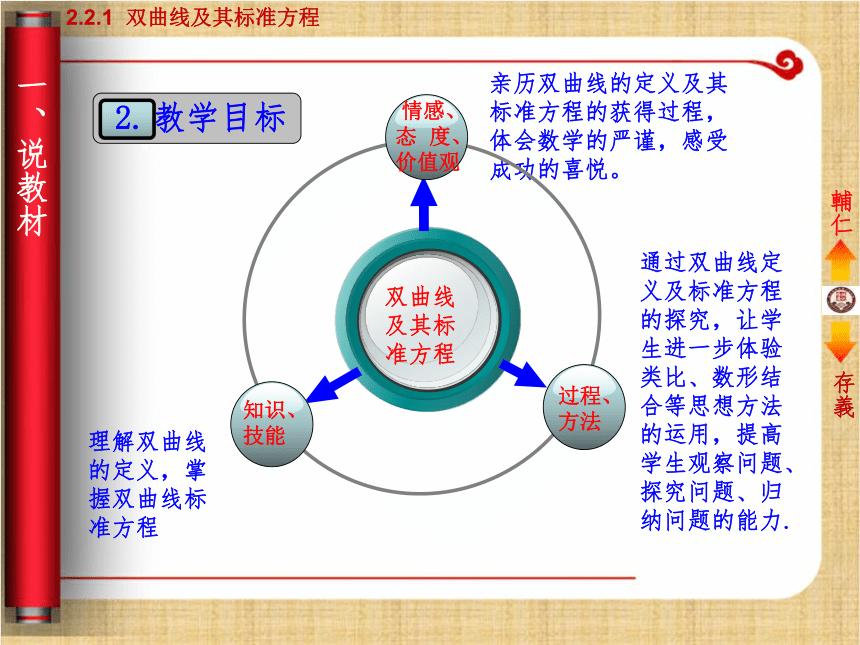
亲历双曲线的定义及其标准方程的获得过程,体会数学的严谨,感受成功的喜悦。
双曲线及其标准方程知识、技能过程、方法 情感、
态 度、
价值观 教学目标一、说教材2.2.2.1 双曲线及其标准方程輔仁存義辅仁存义2.2.1 双曲线及其标准方程 学情分析一、说教材3.辅仁存义2.2.1 双曲线及其标准方程 重点 难点一、说教材教学重点:探究双曲线的定义,推导双曲线 的标准方程.教学难点:双曲线标准方程的推导与化简.4.辅仁存义2.2.1 双曲线及其标准方程二、说方法教学方法:启发式与探究式相结合学法指导:运用类比自主探索、合作交流 教学手段:多媒体辅助教学.辅仁存义2.2.1 双曲线及其标准方程三、说过程辅仁存义2.2.1 双曲线及其标准方程(一)创设情境 引入课题 平面内与两个定点F1、F2的距离之和等于常数( 大于︱F1F2︱)的点的轨迹叫做椭圆.
思考: 若把椭圆定义中的“与两定点的距离之和”改为“距离之差”,这时轨迹又是什么呢?回顾:
平面内与两定点的距离的差等于非零常数的点的轨迹是怎样的图形?2.2.1 双曲线及其标准方程辅仁存义思考:二、动手实践 探索新知2.2.1 双曲线及其标准方程辅仁存义拉链演示思考:2.2.1 双曲线及其标准方程辅仁存义归纳双曲线的定义 平面内与两个定点F1,F2的距离的差 等于常数 的
点的轨迹叫做双曲线.的绝对值2a (小于︱F1F2︱)① 两个定点F1、F2——双曲线的焦点;② |F1F2|=2c ——焦距.(1) .2a < |F1F2 | 双曲线
(2) .2a= |F1F2 |以F1、F2为端点两条射线(3).2a> |F1F2 | 不表示任何图形注意2.2.1 双曲线及其标准方程辅仁 存义挖掘双曲线的定义双曲线的标准方程的推导 如图建立直角坐标系,设M(x ,y)是双曲线上任意一点,F1(-c,0),F2(c,0). 椭圆的标准方程的推导 以F1、F2所在直线为x轴,线段F1F2垂直平分线为y轴,建立坐标系. |F1F2|=2c(c>0),则F1(-c,0)、F2(c,0)设M(x ,y)为椭圆上的任意一点.点M 满足的集合:由两点间距离公式得:(二)、4、动手实践 探索新知双曲线的标准方程的推导平方整理得再平方得即令代入上式,得即即代入上式,得平方整理得再平方得移项得
移项得 椭圆的标准方程的推导(a>0,b>0).想一想焦点在 轴上的标准方程是122=-ba焦点是 F1(-c,0),F2(c,0)焦点在 轴上的标准方程是x辅仁存义2.2.1 双曲线及其标准方程双曲线的标准方程F ( ±c, 0)F(0,±c)(1)双曲线标准方程中 的关系是:(2)双曲线方程中 ,但 不一定大于 ;(4)如果 的系数是正的,那么焦点在 轴上,
如 果 的系数是正的,那么焦点在 轴上.(3)双曲线标准方程中左边用“-”相连,右边为1. 椭圆的标准方程辅仁存义2.2.1 双曲线及其标准方程 双曲线的标准方程练一练 1、判断下列方程是否表示双曲线,若是,写出其焦点的坐标.
, , 辅仁存义2.2.1 双曲线及其标准方程解:(1)是⑵ 是⑶ 不是⑷不是(三)随堂练习 应用新知 F ( ±c, 0) F(0, ± c)| |MF1|-|MF2| | =2a(0 < 2a <|F1F2|)辅仁存义(四)课堂小结 畅谈收获2.2.1 双曲线及其标准方程辅仁存义 作业布置2.2.1 双曲线及其标准方程辅仁存义2.2.1 双曲线及其标准方程板 书 设 计辅仁存义2.2.1 双曲线及其标准方程四、说 反 思在教学过程中,结合类比、数形结合等思想方法,引导学生不断地探究,进而归纳、总结得出结论,既体现学生积极参与的主体地位,又实现教师引导探索的主导作用,真正的体现了“453X”生本课堂教学理念。但双曲线标准方程的推导过程计算量偏大容易导致灌输式教学。辅仁存义2.2.1 双曲线及其标准方程叙永一中 张金虎谢谢您的聆听 请批评指正!
2.2.1双曲线及其标准方程輔仁存義新课标
教材一、说教材 地位和作用1.辅仁存义2.2.1 双曲线及其标准方程叙永一中 张金虎理解双曲线的定义,掌握双曲线标准方程通过双曲线定义及标准方程的探究,让学生进一步体验类比、数形结合等思想方法的运用,提高学生观察问题、探究问题、归纳问题的能力.
亲历双曲线的定义及其标准方程的获得过程,体会数学的严谨,感受成功的喜悦。
双曲线及其标准方程知识、技能过程、方法 情感、
态 度、
价值观 教学目标一、说教材2.2.2.1 双曲线及其标准方程輔仁存義辅仁存义2.2.1 双曲线及其标准方程 学情分析一、说教材3.辅仁存义2.2.1 双曲线及其标准方程 重点 难点一、说教材教学重点:探究双曲线的定义,推导双曲线 的标准方程.教学难点:双曲线标准方程的推导与化简.4.辅仁存义2.2.1 双曲线及其标准方程二、说方法教学方法:启发式与探究式相结合学法指导:运用类比自主探索、合作交流 教学手段:多媒体辅助教学.辅仁存义2.2.1 双曲线及其标准方程三、说过程辅仁存义2.2.1 双曲线及其标准方程(一)创设情境 引入课题 平面内与两个定点F1、F2的距离之和等于常数( 大于︱F1F2︱)的点的轨迹叫做椭圆.
思考: 若把椭圆定义中的“与两定点的距离之和”改为“距离之差”,这时轨迹又是什么呢?回顾:
平面内与两定点的距离的差等于非零常数的点的轨迹是怎样的图形?2.2.1 双曲线及其标准方程辅仁存义思考:二、动手实践 探索新知2.2.1 双曲线及其标准方程辅仁存义拉链演示思考:2.2.1 双曲线及其标准方程辅仁存义归纳双曲线的定义 平面内与两个定点F1,F2的距离的差 等于常数 的
点的轨迹叫做双曲线.的绝对值2a (小于︱F1F2︱)① 两个定点F1、F2——双曲线的焦点;② |F1F2|=2c ——焦距.(1) .2a < |F1F2 | 双曲线
(2) .2a= |F1F2 |以F1、F2为端点两条射线(3).2a> |F1F2 | 不表示任何图形注意2.2.1 双曲线及其标准方程辅仁 存义挖掘双曲线的定义双曲线的标准方程的推导 如图建立直角坐标系,设M(x ,y)是双曲线上任意一点,F1(-c,0),F2(c,0). 椭圆的标准方程的推导 以F1、F2所在直线为x轴,线段F1F2垂直平分线为y轴,建立坐标系. |F1F2|=2c(c>0),则F1(-c,0)、F2(c,0)设M(x ,y)为椭圆上的任意一点.点M 满足的集合:由两点间距离公式得:(二)、4、动手实践 探索新知双曲线的标准方程的推导平方整理得再平方得即令代入上式,得即即代入上式,得平方整理得再平方得移项得
移项得 椭圆的标准方程的推导(a>0,b>0).想一想焦点在 轴上的标准方程是122=-ba焦点是 F1(-c,0),F2(c,0)焦点在 轴上的标准方程是x辅仁存义2.2.1 双曲线及其标准方程双曲线的标准方程F ( ±c, 0)F(0,±c)(1)双曲线标准方程中 的关系是:(2)双曲线方程中 ,但 不一定大于 ;(4)如果 的系数是正的,那么焦点在 轴上,
如 果 的系数是正的,那么焦点在 轴上.(3)双曲线标准方程中左边用“-”相连,右边为1. 椭圆的标准方程辅仁存义2.2.1 双曲线及其标准方程 双曲线的标准方程练一练 1、判断下列方程是否表示双曲线,若是,写出其焦点的坐标.
, , 辅仁存义2.2.1 双曲线及其标准方程解:(1)是⑵ 是⑶ 不是⑷不是(三)随堂练习 应用新知 F ( ±c, 0) F(0, ± c)| |MF1|-|MF2| | =2a(0 < 2a <|F1F2|)辅仁存义(四)课堂小结 畅谈收获2.2.1 双曲线及其标准方程辅仁存义 作业布置2.2.1 双曲线及其标准方程辅仁存义2.2.1 双曲线及其标准方程板 书 设 计辅仁存义2.2.1 双曲线及其标准方程四、说 反 思在教学过程中,结合类比、数形结合等思想方法,引导学生不断地探究,进而归纳、总结得出结论,既体现学生积极参与的主体地位,又实现教师引导探索的主导作用,真正的体现了“453X”生本课堂教学理念。但双曲线标准方程的推导过程计算量偏大容易导致灌输式教学。辅仁存义2.2.1 双曲线及其标准方程叙永一中 张金虎谢谢您的聆听 请批评指正!
