北师大版数学八年级上册 期末质量检测(含答案)
文档属性
| 名称 | 北师大版数学八年级上册 期末质量检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 182.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 19:55:47 | ||
图片预览


文档简介
八年级第一学期期末质量检测
数 学
本试卷满分120分,时间90 分钟.
第Ⅰ卷(选择题 共30分)
1.在 四个数中,最大的数是 ( )
A. |-2| B.2 C.2 D.
2.某班七个合作学习小组人数如下:4,5,5,x,6,7,8,已知这组数据的平均数是6,则这组数据的中位数是 ( )
A.5 B.5.5 C.6 D.7
3.如图,已知△ABC中,AB∥EF,DE∥BC,则图中相等的同位角有 ( )
A.两组 B.三组 C.四组 D.五组
4.下列语句中不是命题的是 ( )
A.对顶角不相等 B.过A、B 两点作直线
C.两点之间线段最短 D.内错角相等
5.正比例函数的图象经过点(-1,2),则这个图象必须经过点 ( )
A.(-2,1) B.(2,-1) C.(1,2) D.(1,-2)
6. 如图,已知D、E在△ABC 的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A 的度数为 ( )
A.100° B.90° C.80° D.70°
7.某校150名学生参加数学竞赛考试,平均每人55分,其中及格人数人均77分,不及格人数人均47分,设及格的学生有x人,不及格的学生有y人,则x,y的值是 ( )
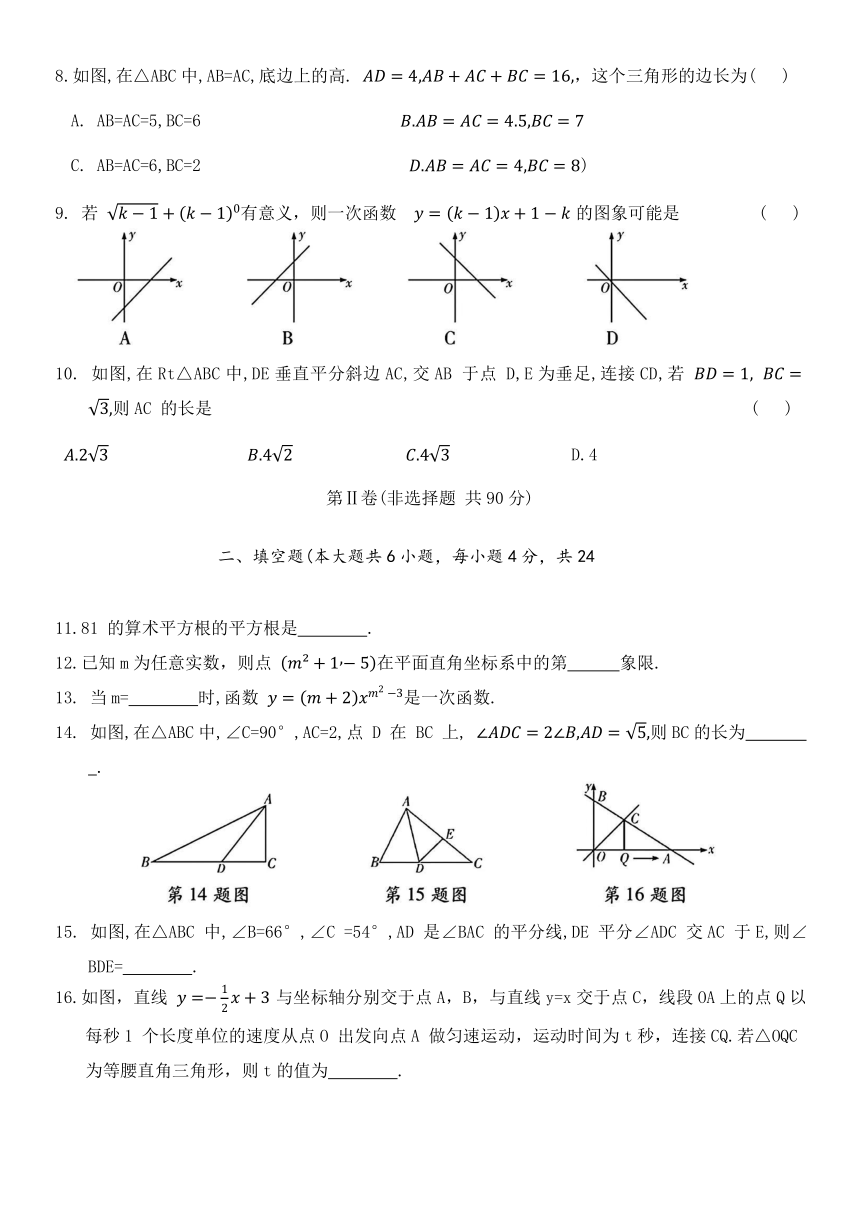
8.如图,在△ABC中,AB=AC,底边上的高. ,这个三角形的边长为( )
A. AB=AC=5,BC=6
C. AB=AC=6,BC=2 )
9. 若 有意义,则一次函数 的图象可能是 ( )
10. 如图,在Rt△ABC中,DE垂直平分斜边AC,交AB 于点 D,E为垂足,连接CD,若 则AC 的长是 ( )
D.4
第Ⅱ卷(非选择题 共90分)
11.81 的算术平方根的平方根是 .
12.已知m为任意实数,则点 在平面直角坐标系中的第 象限.
13. 当m= 时,函数 是一次函数.
14. 如图,在△ABC中,∠C=90°,AC=2,点 D 在 BC 上, 则BC的长为 .
15. 如图,在△ABC 中,∠B=66°,∠C =54°,AD 是∠BAC 的平分线,DE 平分∠ADC 交AC 于E,则∠BDE= .
16.如图,直线 与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1 个长度单位的速度从点O 出发向点A 做匀速运动,运动时间为t秒,连接CQ.若△OQC 为等腰直角三角形,则t的值为 .
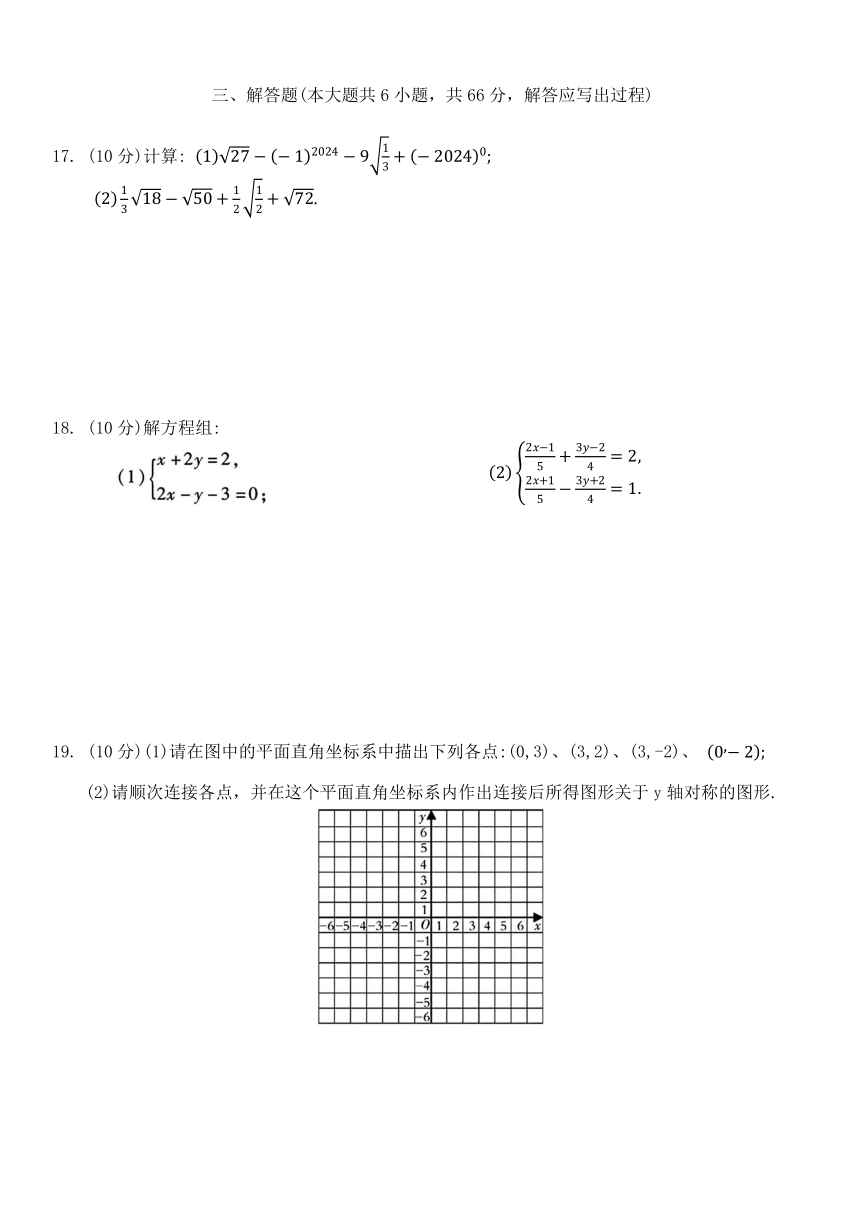
17. (10分)计算:
18. (10分)解方程组:
19. (10分)(1)请在图中的平面直角坐标系中描出下列各点:(0,3)、(3,2)、(3,-2)、
(2)请顺次连接各点,并在这个平面直角坐标系内作出连接后所得图形关于y轴对称的图形.
20.(10分)张华与王强两人的期末6科考试成绩如下表:
政治 语文 英语 数学 物理 化学
张华 88 84 91 96 76 81
王强 83 95 89 93 89 67
(1)求两人的学习成绩的平均数;
(2)现要从中选一人参加除政治外其他五科竞赛,应选谁去 说明理由.
21.(12分)如图,已知 与 都是等腰直角三角形,其中 E 为AB边上一点.
(1)试判断AE 与 BF 的大小关系,并说明理由;
(2)求证:
22.(14分)如图,在平面直角坐标系中,过点 B(6,0)的直线 AB 与直线 OA 相交于点A(4,2),动点 M 在线段OA 和射线AC 上运动.
(1)求直线AB 的解析式;
(2)求 的面积;
(3)是否存在点M,使 的面积是 的面积的 若存在,请直接写出点M的坐标.
1. A 2. C 3. C 4. B 5. D 6. C
7. A 解析:根据题意,得 解得
8. A 9. A
10. A 解析:∵ DE是AC 的垂直平分线,∴AD=DC,∴∠ACD=∠BAC.∵ 在 Rt△BCD 中,BD =1,BC= ,∴∠BDC=60°,∴∠BDC=∠ACD+∠BAC=60°,∴∠BAC=30°, 故选 A.
11. ±3 12. 四 13.2 14. +1 15.132°
16.2 或4 解析:∵由 得C(2,2);如图①,当∠CQO=90°,CQ=OQ,
∵C(2,2),∴OQ=CQ=2,∴t=2;
如 图 ②, 当 ∠OCQ = 90°,
OC=CQ,
过C作CM⊥OA于M,∵C(2,2),∴CM=OM=2,∴QM=OM=2,∴t=2+2=4,即t的值为2或4.
17.解:(1)原式
(2)原式
18.解:(1)原方程组可化为
①+②×2,得
把 代入②,得
所以原方程组的解为
(2).得
把 代入①,得 则
所以原方程组的解为
20.解:(1)张华: (分)
王强: (分)
(2)选王强去,理由如下:
张华其他五科的平均分: 85.6(分)
王强其他五科的平均分:(95 +89 +93 +89 +67)÷5 =
86.6(分)
86.6>85.6,所以应选王强去.
21.(1)解:AE=BF,理由如下:
∵ △ABC 和△EFC 是等腰直角三角形,
∴AC=BC,EC=FC.
∵∠ACB=∠ECF=90°,
∴ ∠ACE=∠ACB -∠ECB=90°-∠ECB,
∠FCB=∠FCE -∠BCE=90°-∠ECB.
∴∠ACE=∠FCB.
在△ACE和△BCF中,
∵AC=BC,∠ACE=∠BCF,CE=CF,∴△ACE≌△BCF,∴AE=BF.
(2)证明:由(1)知:△ACE≌△BCF,AE=BF,
∴∠A=∠CBF.
∵ △ABC 是等腰直角三角形,
∴∠A=∠ABC=45°.
又∵∠A=∠CBF,
∴∠CBF =∠ABC=45°.
∴ ∠EBF =∠ABC+∠CBF=45°+45°=90°.
∴△FBE 是直角三角形.
由勾股定理,得
又·
22.解:(1)设直线AB 的解析式是y= kx+b,
根据题意得
解得
则直线AB 的解析式是y = - x+6.
(2)在y=-x+6中,令x=0,解得y=6.
(3)设OA的解析式是y= mx,则4m=2.
解得
则直线 OA 的解析式是
当△OMC的面积是△OAC的面积的 时,
当M的横坐标是
在 中,当x=1时, 则M的坐标是
在y=-x+6中,x=1则y=5,则M的坐标是(1,5).
则M的坐标是 或
当M 的横坐标是-1,
在y=-x+6中,当x=-1时, 则M 的坐标是
综上所述:M的坐标是 或 或
数 学
本试卷满分120分,时间90 分钟.
第Ⅰ卷(选择题 共30分)
1.在 四个数中,最大的数是 ( )
A. |-2| B.2 C.2 D.
2.某班七个合作学习小组人数如下:4,5,5,x,6,7,8,已知这组数据的平均数是6,则这组数据的中位数是 ( )
A.5 B.5.5 C.6 D.7
3.如图,已知△ABC中,AB∥EF,DE∥BC,则图中相等的同位角有 ( )
A.两组 B.三组 C.四组 D.五组
4.下列语句中不是命题的是 ( )
A.对顶角不相等 B.过A、B 两点作直线
C.两点之间线段最短 D.内错角相等
5.正比例函数的图象经过点(-1,2),则这个图象必须经过点 ( )
A.(-2,1) B.(2,-1) C.(1,2) D.(1,-2)
6. 如图,已知D、E在△ABC 的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A 的度数为 ( )
A.100° B.90° C.80° D.70°
7.某校150名学生参加数学竞赛考试,平均每人55分,其中及格人数人均77分,不及格人数人均47分,设及格的学生有x人,不及格的学生有y人,则x,y的值是 ( )
8.如图,在△ABC中,AB=AC,底边上的高. ,这个三角形的边长为( )
A. AB=AC=5,BC=6
C. AB=AC=6,BC=2 )
9. 若 有意义,则一次函数 的图象可能是 ( )
10. 如图,在Rt△ABC中,DE垂直平分斜边AC,交AB 于点 D,E为垂足,连接CD,若 则AC 的长是 ( )
D.4
第Ⅱ卷(非选择题 共90分)
11.81 的算术平方根的平方根是 .
12.已知m为任意实数,则点 在平面直角坐标系中的第 象限.
13. 当m= 时,函数 是一次函数.
14. 如图,在△ABC中,∠C=90°,AC=2,点 D 在 BC 上, 则BC的长为 .
15. 如图,在△ABC 中,∠B=66°,∠C =54°,AD 是∠BAC 的平分线,DE 平分∠ADC 交AC 于E,则∠BDE= .
16.如图,直线 与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1 个长度单位的速度从点O 出发向点A 做匀速运动,运动时间为t秒,连接CQ.若△OQC 为等腰直角三角形,则t的值为 .
17. (10分)计算:
18. (10分)解方程组:
19. (10分)(1)请在图中的平面直角坐标系中描出下列各点:(0,3)、(3,2)、(3,-2)、
(2)请顺次连接各点,并在这个平面直角坐标系内作出连接后所得图形关于y轴对称的图形.
20.(10分)张华与王强两人的期末6科考试成绩如下表:
政治 语文 英语 数学 物理 化学
张华 88 84 91 96 76 81
王强 83 95 89 93 89 67
(1)求两人的学习成绩的平均数;
(2)现要从中选一人参加除政治外其他五科竞赛,应选谁去 说明理由.
21.(12分)如图,已知 与 都是等腰直角三角形,其中 E 为AB边上一点.
(1)试判断AE 与 BF 的大小关系,并说明理由;
(2)求证:
22.(14分)如图,在平面直角坐标系中,过点 B(6,0)的直线 AB 与直线 OA 相交于点A(4,2),动点 M 在线段OA 和射线AC 上运动.
(1)求直线AB 的解析式;
(2)求 的面积;
(3)是否存在点M,使 的面积是 的面积的 若存在,请直接写出点M的坐标.
1. A 2. C 3. C 4. B 5. D 6. C
7. A 解析:根据题意,得 解得
8. A 9. A
10. A 解析:∵ DE是AC 的垂直平分线,∴AD=DC,∴∠ACD=∠BAC.∵ 在 Rt△BCD 中,BD =1,BC= ,∴∠BDC=60°,∴∠BDC=∠ACD+∠BAC=60°,∴∠BAC=30°, 故选 A.
11. ±3 12. 四 13.2 14. +1 15.132°
16.2 或4 解析:∵由 得C(2,2);如图①,当∠CQO=90°,CQ=OQ,
∵C(2,2),∴OQ=CQ=2,∴t=2;
如 图 ②, 当 ∠OCQ = 90°,
OC=CQ,
过C作CM⊥OA于M,∵C(2,2),∴CM=OM=2,∴QM=OM=2,∴t=2+2=4,即t的值为2或4.
17.解:(1)原式
(2)原式
18.解:(1)原方程组可化为
①+②×2,得
把 代入②,得
所以原方程组的解为
(2).得
把 代入①,得 则
所以原方程组的解为
20.解:(1)张华: (分)
王强: (分)
(2)选王强去,理由如下:
张华其他五科的平均分: 85.6(分)
王强其他五科的平均分:(95 +89 +93 +89 +67)÷5 =
86.6(分)
86.6>85.6,所以应选王强去.
21.(1)解:AE=BF,理由如下:
∵ △ABC 和△EFC 是等腰直角三角形,
∴AC=BC,EC=FC.
∵∠ACB=∠ECF=90°,
∴ ∠ACE=∠ACB -∠ECB=90°-∠ECB,
∠FCB=∠FCE -∠BCE=90°-∠ECB.
∴∠ACE=∠FCB.
在△ACE和△BCF中,
∵AC=BC,∠ACE=∠BCF,CE=CF,∴△ACE≌△BCF,∴AE=BF.
(2)证明:由(1)知:△ACE≌△BCF,AE=BF,
∴∠A=∠CBF.
∵ △ABC 是等腰直角三角形,
∴∠A=∠ABC=45°.
又∵∠A=∠CBF,
∴∠CBF =∠ABC=45°.
∴ ∠EBF =∠ABC+∠CBF=45°+45°=90°.
∴△FBE 是直角三角形.
由勾股定理,得
又·
22.解:(1)设直线AB 的解析式是y= kx+b,
根据题意得
解得
则直线AB 的解析式是y = - x+6.
(2)在y=-x+6中,令x=0,解得y=6.
(3)设OA的解析式是y= mx,则4m=2.
解得
则直线 OA 的解析式是
当△OMC的面积是△OAC的面积的 时,
当M的横坐标是
在 中,当x=1时, 则M的坐标是
在y=-x+6中,x=1则y=5,则M的坐标是(1,5).
则M的坐标是 或
当M 的横坐标是-1,
在y=-x+6中,当x=-1时, 则M 的坐标是
综上所述:M的坐标是 或 或
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
