苏科版九年级数学下册6.3相似图形同步训练(含答案)
文档属性
| 名称 | 苏科版九年级数学下册6.3相似图形同步训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 181.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 00:00:00 | ||
图片预览




文档简介
6.3相似图形同步训练-苏科版九年级数学下册
一、选择题
1.如图,由图形M改变为图形N,这种图形改变属于( )
A.平移 B.轴对称 C.旋转 D.相似
2.下列两个图形一定是相似图形的是( )
A.菱形 B.矩形 C.等腰三角形 D.等边三角形
3.下列说法正确的是( )
A.各边对应成比例的多边形是相似多边形
B.矩形都是相似图形
C.等边三角形都是相似三角形
D.菱形都是相似图形
4.平行于正多边形一边的直线把正多边形分割成两部分,则阴影部分多边形与原多边形相似的是( )
A. B.
C. D.
5.一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边长为( )
A.6 B.8 C.12 D.10
6.两个相似多边形一组对应边分别为3 cm,4.5 cm,那么它们的相似比为( )
A. B. C. D.
7.如图所示,在长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是( )
A.28cm2 B.27cm2 C.21cm2 D.20cm2
8.已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积比为( )
A.4:3 B.3:4 C.16:9 D.9:16
9.下列各组图形不一定相似的是( )
A.两个等腰直角三角形
B.各有一个角是100°的两个等腰三角形
C.各有一个角是50°的两个直角三角形
D.两个矩形
10.如图所示,一般书本的纸张是原纸张多次对开得到的,矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依次类推,若各种开本的矩形都相似,那么等于( )
A.0.618 B. C. D.2
11.如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)的示意图. 已知桌面直径为1.2米,桌面离地面1米. 若灯泡离地面3米,则地面上阴影部分的面积 ( )
A.0.36π米2 B.0.81π米2 C.2π米2 D.3.24π米2
12.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB等于( )
A.4.5米 B.6米 C.7.2米 D.8米
二、填空题
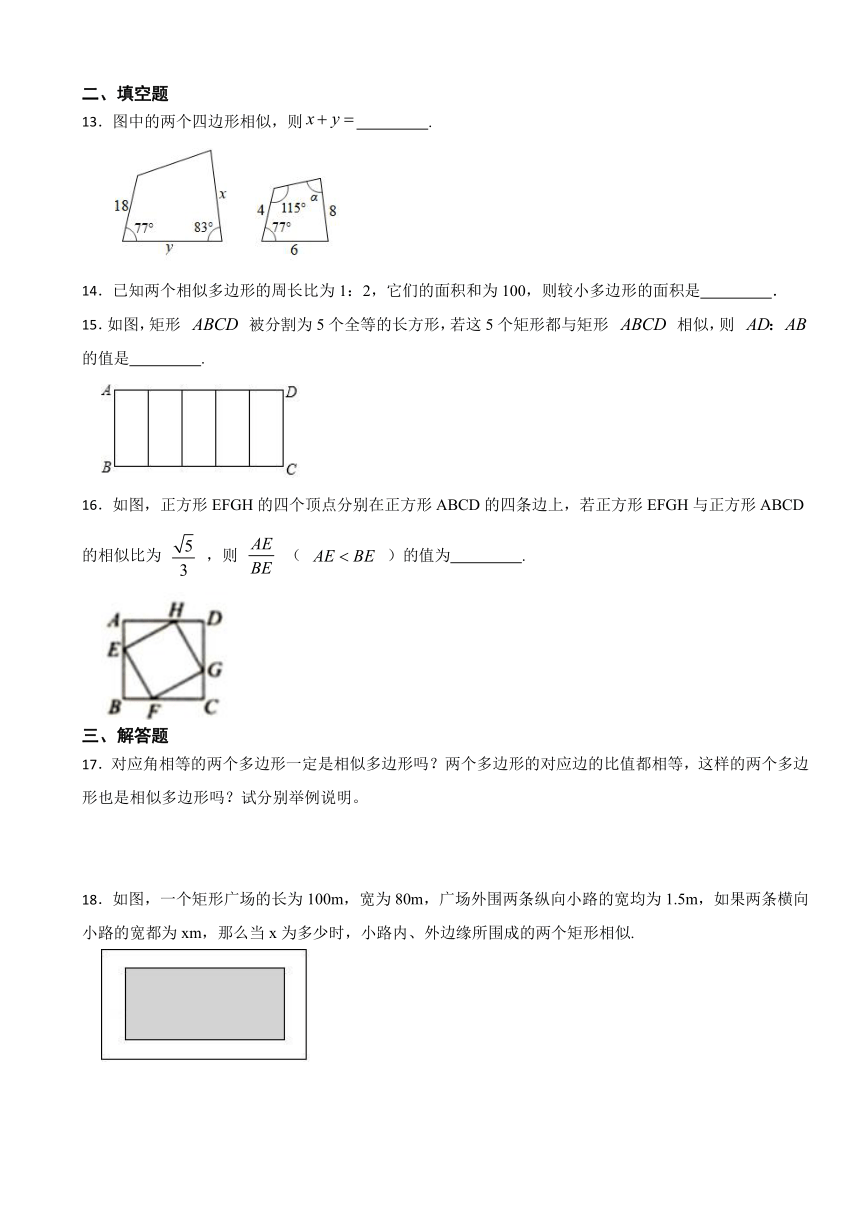
13.图中的两个四边形相似,则 .
14.已知两个相似多边形的周长比为1:2,它们的面积和为100,则较小多边形的面积是 .
15.如图,矩形 被分割为5个全等的长方形,若这5个矩形都与矩形 相似,则 的值是 .
16.如图,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD的相似比为 ,则 ( )的值为 .
三、解答题
17.对应角相等的两个多边形一定是相似多边形吗?两个多边形的对应边的比值都相等,这样的两个多边形也是相似多边形吗?试分别举例说明。
18.如图,一个矩形广场的长为100m,宽为80m,广场外围两条纵向小路的宽均为1.5m,如果两条横向小路的宽都为xm,那么当x为多少时,小路内、外边缘所围成的两个矩形相似.
19.若四边形ABCD与四边形A1B1C1D1相似,相似比为k1= ,又四边形A1B1C1D1与四边形A2B2C2D2相似,相似比为k2= ,请问四边形ABCD与四边形A2B2C2D2相似吗?若相似,相似比是多少?
20.为了铺设一矩形场地,特意选择某地砖进行密铺,为了使每一部分都铺成如图所示的形状,且由8块地砖组成,问:
(1)每块地砖的长与宽分别为多少?
(2)这样的地砖与所铺成的矩形地面是否相似?试明你的结论.
答案解析部分
1.【答案】D
【解析】解:图形M改变为图形N,是相似变换.
故答案为:D.
2.【答案】D
【解析】解:A、两个菱形的对应边的比相等,但对应角不一定相等,不一定是相似图形,故此选项不符合题意;
B、两个矩形的对应角相等,但对应边的比不一定相等,不一定是相似图形,故此选项不符合题意;
C、两等腰三角形不一定相似,故此选项不符合题意;
D、两个等边三角形的对应边的比相等,对应角一定相等,故两个等边三角形一定相似,故此选项符合题意.
故答案为:D.
3.【答案】C
【解析】【分析】根据相似图形的定义,对应边成比例,对应角相等对各选项分析判断后利用排除法求解.
A、各边对应成比例的多边形对应角不一定相等(如菱形),所以不一定是相似多边形,故本选项错误;
B、矩形对应角相等,对应边不一定成比例,所以不一定是相似图形,故本选项错误;
C、等边三角形对应角相等,对应边成比例,所以是相似三角形,故本选项正确;
D、菱形对应边成比例,对应角不一定相等,所以不一定是相似图形,故本选项错误.
故选C.
4.【答案】A
【解析】解:A、阴影三角形与原三角形的对应角相等、对应边的比相等,符合相似多边形的定义,正确;
B、阴影矩形与原矩形的对应角相等,但对应边不成比例,不符合相似多边形的定义,错误;
C、阴影五边形与原五边形的对应角相等,但对应边不成比例,不符合相似多边形的定义,错误;
D、阴影六边形与原六边形的对应角相等,但对应边不成比例,不符合相似多边形的定,错误.
故答案为:A.
5.【答案】B
【解析】设这个多边形的最长边是x, 则 ,
解得x=8。
故答案为:B.
6.【答案】A
【解析】由题意得,两个相似多边形的一组对应边的比为3:4.5= ,
∴它们的相似比为 .
故答案为:A.
7.【答案】B
【解析】解:如图,
依题意,在矩形ABDC中截取矩形ABFE,
则矩形ABDC∽矩形FDCE,
则 AE/DF=BD/DC
设DF=xcm,得到:6/x=8/6
解得:x=4.5,
则剩下的矩形面积是:4.5×6=27cm2.
8.【答案】D
【解析】【分析】已知相似三角形的相似比,根据相似三角形的面积比等于相似比的平方可直接得出答案。
∵△ABC∽△DEF,且相似比为3:4,
∴△DEF与△ABC的面积比为32:42,
即△ABC与△DEF的面积比为9:16.
故选D.
9.【答案】D
【解析】A、两个等腰直角三角形,对应边成比例,对应角相等,符合定义,一定相似,故本选项正确;
B、各有一个角是100°的两个等腰三角形,100°的角一定是顶角,一定相似,故本选项正确;
C、各有一个角是50°的两个直角三角形,都有一个直角,根据两角对应相等,两三角形相似,故本选项正确;
D、两个矩形,四个角都是直角,但四条边不一定对应成比例,不一定相似,故本选项错误.
故选D.
10.【答案】C
【解析】【分析】根据矩形ABCD的面积是矩形ABFE面积的2倍,得出相似图形面积比是相似比的平方,进而得出的值.
∵矩形ABCD的面积是矩形ABFE面积的2倍,各种开本的矩形都相似,
∴()2=2,
∴=.
故选C.
11.【答案】B
【解析】【分析】桌面离地面1米.若灯泡离地面3米,则灯泡离桌面是2米,桌面与阴影是相似图形,相似比是2:3,两个图形的半径的比就是相似比,设阴影部分的直径是xm,则1.2:x=2:3解得:x=1.8,因而地面上阴影部分的面积为0.81π米2.
设阴影部分的直径是xm,则
1.2:x=2:3
解得x=1.8,
所以地面上阴影部分的面积为:S=πr2=0.81πm2.
故选B.
12.【答案】B
【解析】【分析】由于人和地面是垂直的,即和路灯到地面的垂线平行,构成两组相似.根据对应边成比例,列方程解答即可.
解:如图,
GC⊥BC,AB⊥BC,
∴GC∥AB,
∴△GCD∽△ABD(两个角对应相等的两个三角形相似),
∴,
设BC=x,则,
∴x=3,
∴AB=6.
故选:B.
13.【答案】63
【解析】解:∵两个四边形相似,
∴,
∴,
∴,
故答案为:63.
14.【答案】20
【解析】解:∵两个相似多边形的周长比为1:2,
∴两个相似多边形的面积比为1:4,
设较小多边形的面积为,较大多边形的面积为,则:=1:4,
,
它们的面积和为100,
,
.
故答案为:20.
15.【答案】
【解析】解:
设AE=a,
∵五个小矩形全等,
∴AD=5AE=5a,
∵每个小矩形都与矩形ABCD相似
∴ = ,
∴AB2=AD AE=5AE2=5a2,
AB= a,
∴AD:AB=5a: a= .
故答案为: .
16.【答案】
【解析】解:在正方形EFGH与正方形ABCD中,
∠A=∠B=90°,EF=EH,∠FEH=90°,
∴∠AEH+∠AHE=90°,∠BEF+∠AEH=90°,
∴∠AHE=∠BEF,
∴△AEH≌△BFE(AAS),
∴BE=AH,
∵ ,
令EH= ,AB= ,
在直角三角形AEH中,设AE= ,AH=AB-AE= ,
由勾股定理,得 ,
即 ,
解得: 或 ,
∵ ,
∴ ,
∴ ,
∴ ;
故答案为: .
17.【答案】解:对应角相等的两个多边形未必相似,如矩形和正方形;两个多边形的对应边成比例,这两个多边形未必相似,如;菱形和正方形.
【解析】对应角相等的两个多边形不一定相似,如矩形;对应边成比例的两个多边形不一定相似,如菱形。
18.【答案】解:当 时,小路内、外边缘所围成的两个矩形相似.
解得x=1.2
答:当x为1.2m时,小路内、外边缘所围成的两个矩形相似.
【解析】根据两个矩形相似可得比例式,于是可列方程求解。
19.【答案】解:相似.
理由:∵四边形ABCD与四边形A1B1C1D1相似,四边形A1B1C1D1与四边形A2B2C2D2相似,
∴四边形ABCD与四边形A2B2C2D2相似;
∵四边形ABCD与四边形A1B1C1D1相似,相似比为k1= ,又四边形A1B1C1D1与四边形A2B2C2D2相似,相似比为k2= ,
∴四边形ABCD与四边形A2B2C2D2相似比是:
20.【答案】(1)解:设矩形地砖的长为a cm,宽为b cm,
由题图可知4b=60,即b=15.
因为 所以
所以矩形地砖的长为45 cm,宽为15 cm.
(2)解:不相似.理由:因为所铺成矩形地面的长为 (cm),宽为60 cm,
所以大矩形的长与宽之比为:
而小矩形的长与宽之比为:
即所铺成的矩形地面的长与宽和地砖的长与宽不成比例.
所以它们不相似.
一、选择题
1.如图,由图形M改变为图形N,这种图形改变属于( )
A.平移 B.轴对称 C.旋转 D.相似
2.下列两个图形一定是相似图形的是( )
A.菱形 B.矩形 C.等腰三角形 D.等边三角形
3.下列说法正确的是( )
A.各边对应成比例的多边形是相似多边形
B.矩形都是相似图形
C.等边三角形都是相似三角形
D.菱形都是相似图形
4.平行于正多边形一边的直线把正多边形分割成两部分,则阴影部分多边形与原多边形相似的是( )
A. B.
C. D.
5.一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边长为( )
A.6 B.8 C.12 D.10
6.两个相似多边形一组对应边分别为3 cm,4.5 cm,那么它们的相似比为( )
A. B. C. D.
7.如图所示,在长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是( )
A.28cm2 B.27cm2 C.21cm2 D.20cm2
8.已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积比为( )
A.4:3 B.3:4 C.16:9 D.9:16
9.下列各组图形不一定相似的是( )
A.两个等腰直角三角形
B.各有一个角是100°的两个等腰三角形
C.各有一个角是50°的两个直角三角形
D.两个矩形
10.如图所示,一般书本的纸张是原纸张多次对开得到的,矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依次类推,若各种开本的矩形都相似,那么等于( )
A.0.618 B. C. D.2
11.如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)的示意图. 已知桌面直径为1.2米,桌面离地面1米. 若灯泡离地面3米,则地面上阴影部分的面积 ( )
A.0.36π米2 B.0.81π米2 C.2π米2 D.3.24π米2
12.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB等于( )
A.4.5米 B.6米 C.7.2米 D.8米
二、填空题
13.图中的两个四边形相似,则 .
14.已知两个相似多边形的周长比为1:2,它们的面积和为100,则较小多边形的面积是 .
15.如图,矩形 被分割为5个全等的长方形,若这5个矩形都与矩形 相似,则 的值是 .
16.如图,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD的相似比为 ,则 ( )的值为 .
三、解答题
17.对应角相等的两个多边形一定是相似多边形吗?两个多边形的对应边的比值都相等,这样的两个多边形也是相似多边形吗?试分别举例说明。
18.如图,一个矩形广场的长为100m,宽为80m,广场外围两条纵向小路的宽均为1.5m,如果两条横向小路的宽都为xm,那么当x为多少时,小路内、外边缘所围成的两个矩形相似.
19.若四边形ABCD与四边形A1B1C1D1相似,相似比为k1= ,又四边形A1B1C1D1与四边形A2B2C2D2相似,相似比为k2= ,请问四边形ABCD与四边形A2B2C2D2相似吗?若相似,相似比是多少?
20.为了铺设一矩形场地,特意选择某地砖进行密铺,为了使每一部分都铺成如图所示的形状,且由8块地砖组成,问:
(1)每块地砖的长与宽分别为多少?
(2)这样的地砖与所铺成的矩形地面是否相似?试明你的结论.
答案解析部分
1.【答案】D
【解析】解:图形M改变为图形N,是相似变换.
故答案为:D.
2.【答案】D
【解析】解:A、两个菱形的对应边的比相等,但对应角不一定相等,不一定是相似图形,故此选项不符合题意;
B、两个矩形的对应角相等,但对应边的比不一定相等,不一定是相似图形,故此选项不符合题意;
C、两等腰三角形不一定相似,故此选项不符合题意;
D、两个等边三角形的对应边的比相等,对应角一定相等,故两个等边三角形一定相似,故此选项符合题意.
故答案为:D.
3.【答案】C
【解析】【分析】根据相似图形的定义,对应边成比例,对应角相等对各选项分析判断后利用排除法求解.
A、各边对应成比例的多边形对应角不一定相等(如菱形),所以不一定是相似多边形,故本选项错误;
B、矩形对应角相等,对应边不一定成比例,所以不一定是相似图形,故本选项错误;
C、等边三角形对应角相等,对应边成比例,所以是相似三角形,故本选项正确;
D、菱形对应边成比例,对应角不一定相等,所以不一定是相似图形,故本选项错误.
故选C.
4.【答案】A
【解析】解:A、阴影三角形与原三角形的对应角相等、对应边的比相等,符合相似多边形的定义,正确;
B、阴影矩形与原矩形的对应角相等,但对应边不成比例,不符合相似多边形的定义,错误;
C、阴影五边形与原五边形的对应角相等,但对应边不成比例,不符合相似多边形的定义,错误;
D、阴影六边形与原六边形的对应角相等,但对应边不成比例,不符合相似多边形的定,错误.
故答案为:A.
5.【答案】B
【解析】设这个多边形的最长边是x, 则 ,
解得x=8。
故答案为:B.
6.【答案】A
【解析】由题意得,两个相似多边形的一组对应边的比为3:4.5= ,
∴它们的相似比为 .
故答案为:A.
7.【答案】B
【解析】解:如图,
依题意,在矩形ABDC中截取矩形ABFE,
则矩形ABDC∽矩形FDCE,
则 AE/DF=BD/DC
设DF=xcm,得到:6/x=8/6
解得:x=4.5,
则剩下的矩形面积是:4.5×6=27cm2.
8.【答案】D
【解析】【分析】已知相似三角形的相似比,根据相似三角形的面积比等于相似比的平方可直接得出答案。
∵△ABC∽△DEF,且相似比为3:4,
∴△DEF与△ABC的面积比为32:42,
即△ABC与△DEF的面积比为9:16.
故选D.
9.【答案】D
【解析】A、两个等腰直角三角形,对应边成比例,对应角相等,符合定义,一定相似,故本选项正确;
B、各有一个角是100°的两个等腰三角形,100°的角一定是顶角,一定相似,故本选项正确;
C、各有一个角是50°的两个直角三角形,都有一个直角,根据两角对应相等,两三角形相似,故本选项正确;
D、两个矩形,四个角都是直角,但四条边不一定对应成比例,不一定相似,故本选项错误.
故选D.
10.【答案】C
【解析】【分析】根据矩形ABCD的面积是矩形ABFE面积的2倍,得出相似图形面积比是相似比的平方,进而得出的值.
∵矩形ABCD的面积是矩形ABFE面积的2倍,各种开本的矩形都相似,
∴()2=2,
∴=.
故选C.
11.【答案】B
【解析】【分析】桌面离地面1米.若灯泡离地面3米,则灯泡离桌面是2米,桌面与阴影是相似图形,相似比是2:3,两个图形的半径的比就是相似比,设阴影部分的直径是xm,则1.2:x=2:3解得:x=1.8,因而地面上阴影部分的面积为0.81π米2.
设阴影部分的直径是xm,则
1.2:x=2:3
解得x=1.8,
所以地面上阴影部分的面积为:S=πr2=0.81πm2.
故选B.
12.【答案】B
【解析】【分析】由于人和地面是垂直的,即和路灯到地面的垂线平行,构成两组相似.根据对应边成比例,列方程解答即可.
解:如图,
GC⊥BC,AB⊥BC,
∴GC∥AB,
∴△GCD∽△ABD(两个角对应相等的两个三角形相似),
∴,
设BC=x,则,
∴x=3,
∴AB=6.
故选:B.
13.【答案】63
【解析】解:∵两个四边形相似,
∴,
∴,
∴,
故答案为:63.
14.【答案】20
【解析】解:∵两个相似多边形的周长比为1:2,
∴两个相似多边形的面积比为1:4,
设较小多边形的面积为,较大多边形的面积为,则:=1:4,
,
它们的面积和为100,
,
.
故答案为:20.
15.【答案】
【解析】解:
设AE=a,
∵五个小矩形全等,
∴AD=5AE=5a,
∵每个小矩形都与矩形ABCD相似
∴ = ,
∴AB2=AD AE=5AE2=5a2,
AB= a,
∴AD:AB=5a: a= .
故答案为: .
16.【答案】
【解析】解:在正方形EFGH与正方形ABCD中,
∠A=∠B=90°,EF=EH,∠FEH=90°,
∴∠AEH+∠AHE=90°,∠BEF+∠AEH=90°,
∴∠AHE=∠BEF,
∴△AEH≌△BFE(AAS),
∴BE=AH,
∵ ,
令EH= ,AB= ,
在直角三角形AEH中,设AE= ,AH=AB-AE= ,
由勾股定理,得 ,
即 ,
解得: 或 ,
∵ ,
∴ ,
∴ ,
∴ ;
故答案为: .
17.【答案】解:对应角相等的两个多边形未必相似,如矩形和正方形;两个多边形的对应边成比例,这两个多边形未必相似,如;菱形和正方形.
【解析】对应角相等的两个多边形不一定相似,如矩形;对应边成比例的两个多边形不一定相似,如菱形。
18.【答案】解:当 时,小路内、外边缘所围成的两个矩形相似.
解得x=1.2
答:当x为1.2m时,小路内、外边缘所围成的两个矩形相似.
【解析】根据两个矩形相似可得比例式,于是可列方程求解。
19.【答案】解:相似.
理由:∵四边形ABCD与四边形A1B1C1D1相似,四边形A1B1C1D1与四边形A2B2C2D2相似,
∴四边形ABCD与四边形A2B2C2D2相似;
∵四边形ABCD与四边形A1B1C1D1相似,相似比为k1= ,又四边形A1B1C1D1与四边形A2B2C2D2相似,相似比为k2= ,
∴四边形ABCD与四边形A2B2C2D2相似比是:
20.【答案】(1)解:设矩形地砖的长为a cm,宽为b cm,
由题图可知4b=60,即b=15.
因为 所以
所以矩形地砖的长为45 cm,宽为15 cm.
(2)解:不相似.理由:因为所铺成矩形地面的长为 (cm),宽为60 cm,
所以大矩形的长与宽之比为:
而小矩形的长与宽之比为:
即所铺成的矩形地面的长与宽和地砖的长与宽不成比例.
所以它们不相似.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
