【2025春新教材】人教版七年级下册数学8.2 立方根 教学设计
文档属性
| 名称 | 【2025春新教材】人教版七年级下册数学8.2 立方根 教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 643.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 00:00:00 | ||
图片预览




文档简介
/ 让教学更有效 高效备课 | 数学学科
8.2 立方根教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册第八章 实数 8.2立方根,内容包括:立方根
2.内容解析
本节课是在前面学习了立方运算,平方根和算术平方根的基础上安排的,之前立方,平方根和算术平方根学习为这节课奠定了方法基础和知识基础,立方根的学习也是学习实数的准备知识,提供了知识积累. 新课标中提出,义务教育阶段的数学课程,要从数学本身的特点出发,从学生学习数学的心理规律和学生已有的知识经验出发,让学生经历一个实践、思考、探索、交流、解释、应用的学习过程,本节课就在这个思想的指导下设计的.教材通过类比平方根设置唤醒学生探究交流的激情,让学生在类比、探索、交流的过程中感悟立方根的意义,同时让学生在学习知识技能的同时,注意数学思想方法和良好学习习惯的养成,使学生体验数学的“实践第一”和数学来源于实践,又服务于实践的思想.
基于以上分析,本节课的教学重点是: 理解立方根的定义并且会求一个数的立方根.
二、目标和目标解析
1.目标
(1)理解立方根的定义并且会求一个数的立方根;
(2)会表示一个数的立方根和理解立方根的性质;
(3)会用估值法比较两个数的大小和掌握被开方数和立方根近似值的小数点的移动规律,并能利用规律解题.
2.目标解析
(1)教材类比平方根引入,利于激发学生的学习兴趣和好奇心.学生通过计算,观察,类比,总结,归纳立方根的定义,有利于学生充分理解和牢固掌握立方根的定义.通过小组讨论,培养合作精神,让学生在探索问题的过程中,体验解决问题的方法和乐趣,增强学习兴趣.
(2)学生能根据估值法或者计算器计算比较两个数的大小,掌握估算方法,形成估算意识.
(3)了解用计算器计算立方根的大小,掌握被开方数和其立方根近似值的小数点的移动规律,并能利用规律解题.
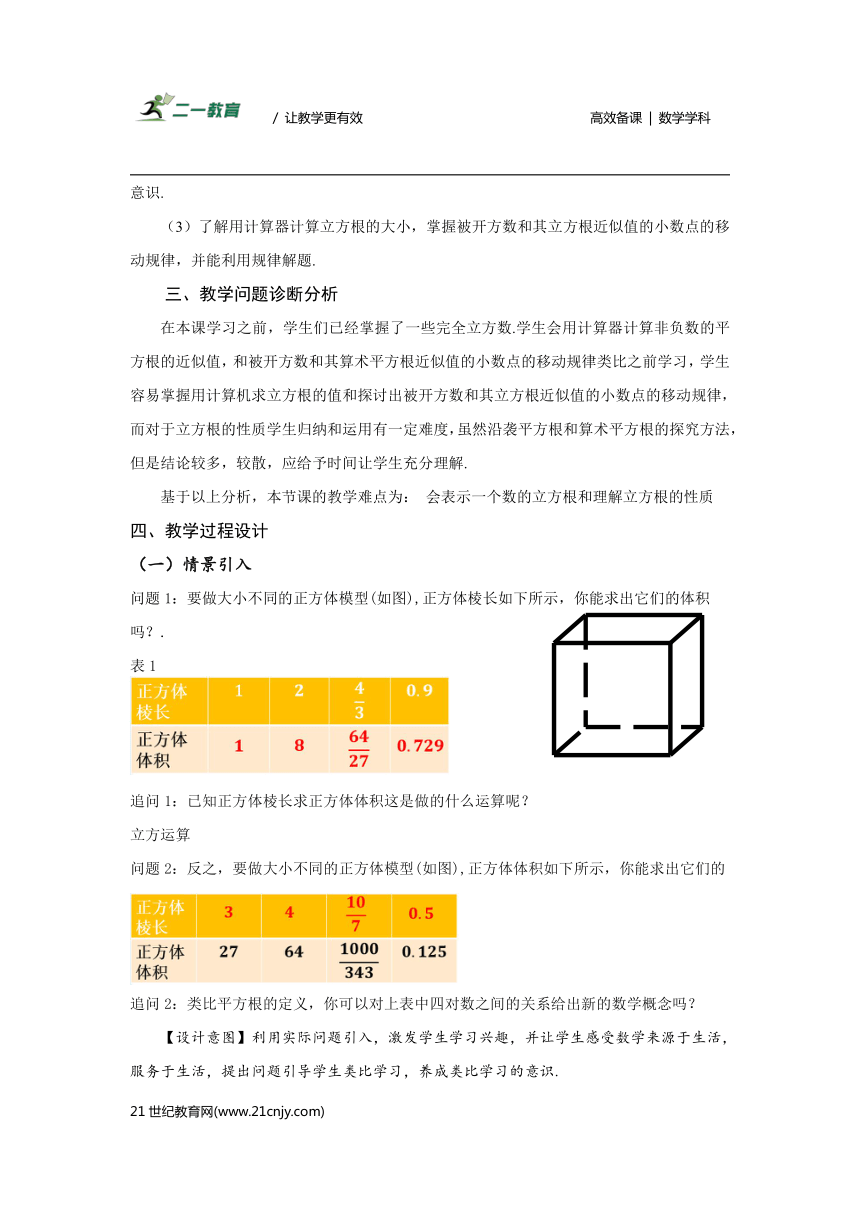
三、教学问题诊断分析
在本课学习之前,学生们已经掌握了一些完全立方数.学生会用计算器计算非负数的平方根的近似值,和被开方数和其算术平方根近似值的小数点的移动规律类比之前学习,学生容易掌握用计算机求立方根的值和探讨出被开方数和其立方根近似值的小数点的移动规律,而对于立方根的性质学生归纳和运用有一定难度,虽然沿袭平方根和算术平方根的探究方法,但是结论较多,较散,应给予时间让学生充分理解.
基于以上分析,本节课的教学难点为: 会表示一个数的立方根和理解立方根的性质
四、教学过程设计
(一)情景引入
问题1:要做大小不同的正方体模型(如图),正方体棱长如下所示,你能求出它们的体积吗?.
表1
追问1:已知正方体棱长求正方体体积这是做的什么运算呢?
立方运算
问题2:反之,要做大小不同的正方体模型(如图),正方体体积如下所示,你能求出它们的棱长吗?.
追问2:类比平方根的定义,你可以对上表中四对数之间的关系给出新的数学概念吗?
【设计意图】利用实际问题引入,激发学生学习兴趣,并让学生感受数学来源于生活,服务于生活,提出问题引导学生类比学习,养成类比学习的意识.
(二)新知讲解
一般地,一个数的立方等于,即这个数就叫作的立方根,或者叫作的三次方根.
追问3.类比开方的运算的定义,你可以对表2中的运算给出新的数学概念吗?
求一个数的立方根的运算,叫作开立方.
1.根据立方意义填空
(1)因为所以的立方根是1
(2)因为,所以0.064的立方是(0.4 ) ;
(3)因为,所以的立方根是(0 ) ;
(4)因为,所以的立方根是( ).
(5)因为 ,所以的立方根是( ) ;
归纳:①正数,负数,0都有且只有一个立方根.
②正数的立方根是正数.负数的立方根是负数.0的立方根是0.
③被开方数互为倒数,立方根也互为倒数.
2:判断下列说法是否正确, 并说明理由.
(1)的立方根是 ( x )
(2)25的平方根是5 ( x )
(3)-64没有立方根 ( x )
(4)-4的平方根是±2 ( x )
(5)的立方根是2 ( x )
(6) 0的平方根和立方根都是0 ( √ )
归纳:平方等于本身的数:
立方等于本身的数:
平方根等于本身的数:
算术平方根等于本身的数:
立方根等于本身的数:
立方根的表示方法
问:若有意义,求的取值范围?任意实数
【设计意图】通过类比平方根的定义,引导学生归纳得出立方根的定义,再通过计算求立方根的正反例判断,更利于学生结合实际例子理解立方根的定义,一题一总结,有利于培养学生观察,归纳,总结的能力.
(三)典例讲解
例1 求下列各数的立方根
(1) (2) (3) (4)
解(1)∵的立方根是,即
(2)∵,∴的立方根是即
(3)∵,∴的立方根是,即
(4)∵,∴的立方根是,即
例2说出下列各式的意义,并求它们的值
(1) (2) (3) (4)
解(1)729的立方根;
(2)的立方根的相反数;
(3)的立方根的相反数;
(4)的立方的立方根;
方法:求带分数的立方根应先化为假分数
例3.计算(1) (2)
(3). (4)
解(1)原式 (2)原式
原式 (4)原式
总结:平方根与立方根的区别和联系
【设计意图】通过上题练习让学生牢固掌握立方根的定义并能用定义求一个数的立方根,并理解立方根的表示方式,会表示一个数的立方根.
(四)针对训练
1.若=2,=4,求的值.
解:∵=2,=4,
∴,
∴
∴或
∴ == 4 或 ==0.
2.已知是的算术平方根,的立方根,求的值
解:∵ 由题意可得
∴
∵ ,
∴
∴
3.求未知数的值
(1) (2)
(3) (4)
解(1)∵
∴
解得:
(2)原方程变形为:
∵
∴
解得:
解(1)∵
∴
解得:
(2)原方程变形为:
∵
∴
解得:
【设计意图】通过练习让学生熟练地掌握立方根的定义并能用其解题,考查学生的综合解题能力.
(五)变式训练
1.【问题发现】(1)计算下列各式
①_____1_______; _____1_____.
②__________; __________.
③___________; __________;
(2)观察上面式子及其计算结果,你能得到什么结论?
结论:①如果被开方数互为相反数,那么它们的立方根也互为相反数即:
②被开方数大,其立方根大,被开方数小,其立方根小.
1.【知识应用】计算下列各式
① ② ③
解①
②
③
1.【知识迁移】(1)已知+,且的平方根是它本身,求xy的立方根
解:∵ 和互为相反数
∴,解得
∵的平方根是它本身
∴,解得
∴
易错易混辨析
若则
若则
1.【知识迁移】(2) 比较下列各组数的大小.
(1)与 (2)与 (3)与
解(1)法一:立方法
∵
∴
法二:估值法(夹逼法)
∵
∴
∴
法三:计算器
∵ 按键顺序:
∴
解(2)∵,
∴
(3)∵
∵
∴
【设计意图】通过此题一题多解发展学生的发散思维,并总结比较大小的两种常用方法:①平方法,②估值法. 发展学生估值的思维,养成估值的意识.
(六)拓展探究
1.已知的立方根是,的算术平方根是,是的整数部分,求的平方根.
解:∵的立方根是,的算术平方根是
∴
∴
∵
∴
∴
∴
∴
2.(1)计算下列各式的值,你能发现什么规律
规律:被开方数扩大(缩小)1000倍时,它的立方根扩大(缩小)10倍.
(2)利用(1)中的结论,如果,那么_13.33______
【设计意图】1题主要培养学生综合分析,综合运用和综合解题的能力,2题培养学生类比,观察,猜想,归纳的能力,并运用所得知识解决问题的能力.
(七)当堂检测
1.的立方根用符号表示,正确的是( C )
A. B. C. D.
2.有理数-8的立方根是( A )
A.-2 B.2 C.±2 D.±4
3.下列各组数中,互为相反数的一组是( A )
A.与 B. 与
C.与 D. 与
4.计算
(1)_____0.4_____;(2)______;
(3)____1_______;(4)_____ ______;
(5)的立方根是____-2______
(6)的平方根是________
(7)若则的值为__14____
(8)若,则的取值范围__m<2_____
(9)和之间的整数是 5 .
5.计算(1)
(2)
(3)
解(1)原式
(2)原式
(3)原式
6.求未知数的值
(1) (2)
解(1)原方程变形为:
∵
∴
解得:
(2)原方程变形为:
∵
∴解得:
7.已知的平方根是±3,的立方根是2,求的算术平方根
解:∵的平方根是±3
∴即
∵的立方根是2
∴
∴
∴
8.已知和互为相反数,求的值.
解:根据题意,得
∴
∴
∴
【设计意图】针对本节课所学,巩固学生理解立方根的概念,会求一个数的立方根,会利用立方根解决问题,培养学生综合解题的能力.
(八)小结梳理
【设计意图】通过课堂小结,使学生对本节课的知识有一个系统的回顾和认识,进而形成一个清晰的脉络,加深学生对本节课知识的理解与掌握.
(九)布置作业
必做题P49.练习1,2,3,选做题P51练习8,9题.
五、教学反思
21世纪教育网(www.21cnjy.com)
8.2 立方根教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册第八章 实数 8.2立方根,内容包括:立方根
2.内容解析
本节课是在前面学习了立方运算,平方根和算术平方根的基础上安排的,之前立方,平方根和算术平方根学习为这节课奠定了方法基础和知识基础,立方根的学习也是学习实数的准备知识,提供了知识积累. 新课标中提出,义务教育阶段的数学课程,要从数学本身的特点出发,从学生学习数学的心理规律和学生已有的知识经验出发,让学生经历一个实践、思考、探索、交流、解释、应用的学习过程,本节课就在这个思想的指导下设计的.教材通过类比平方根设置唤醒学生探究交流的激情,让学生在类比、探索、交流的过程中感悟立方根的意义,同时让学生在学习知识技能的同时,注意数学思想方法和良好学习习惯的养成,使学生体验数学的“实践第一”和数学来源于实践,又服务于实践的思想.
基于以上分析,本节课的教学重点是: 理解立方根的定义并且会求一个数的立方根.
二、目标和目标解析
1.目标
(1)理解立方根的定义并且会求一个数的立方根;
(2)会表示一个数的立方根和理解立方根的性质;
(3)会用估值法比较两个数的大小和掌握被开方数和立方根近似值的小数点的移动规律,并能利用规律解题.
2.目标解析
(1)教材类比平方根引入,利于激发学生的学习兴趣和好奇心.学生通过计算,观察,类比,总结,归纳立方根的定义,有利于学生充分理解和牢固掌握立方根的定义.通过小组讨论,培养合作精神,让学生在探索问题的过程中,体验解决问题的方法和乐趣,增强学习兴趣.
(2)学生能根据估值法或者计算器计算比较两个数的大小,掌握估算方法,形成估算意识.
(3)了解用计算器计算立方根的大小,掌握被开方数和其立方根近似值的小数点的移动规律,并能利用规律解题.
三、教学问题诊断分析
在本课学习之前,学生们已经掌握了一些完全立方数.学生会用计算器计算非负数的平方根的近似值,和被开方数和其算术平方根近似值的小数点的移动规律类比之前学习,学生容易掌握用计算机求立方根的值和探讨出被开方数和其立方根近似值的小数点的移动规律,而对于立方根的性质学生归纳和运用有一定难度,虽然沿袭平方根和算术平方根的探究方法,但是结论较多,较散,应给予时间让学生充分理解.
基于以上分析,本节课的教学难点为: 会表示一个数的立方根和理解立方根的性质
四、教学过程设计
(一)情景引入
问题1:要做大小不同的正方体模型(如图),正方体棱长如下所示,你能求出它们的体积吗?.
表1
追问1:已知正方体棱长求正方体体积这是做的什么运算呢?
立方运算
问题2:反之,要做大小不同的正方体模型(如图),正方体体积如下所示,你能求出它们的棱长吗?.
追问2:类比平方根的定义,你可以对上表中四对数之间的关系给出新的数学概念吗?
【设计意图】利用实际问题引入,激发学生学习兴趣,并让学生感受数学来源于生活,服务于生活,提出问题引导学生类比学习,养成类比学习的意识.
(二)新知讲解
一般地,一个数的立方等于,即这个数就叫作的立方根,或者叫作的三次方根.
追问3.类比开方的运算的定义,你可以对表2中的运算给出新的数学概念吗?
求一个数的立方根的运算,叫作开立方.
1.根据立方意义填空
(1)因为所以的立方根是1
(2)因为,所以0.064的立方是(0.4 ) ;
(3)因为,所以的立方根是(0 ) ;
(4)因为,所以的立方根是( ).
(5)因为 ,所以的立方根是( ) ;
归纳:①正数,负数,0都有且只有一个立方根.
②正数的立方根是正数.负数的立方根是负数.0的立方根是0.
③被开方数互为倒数,立方根也互为倒数.
2:判断下列说法是否正确, 并说明理由.
(1)的立方根是 ( x )
(2)25的平方根是5 ( x )
(3)-64没有立方根 ( x )
(4)-4的平方根是±2 ( x )
(5)的立方根是2 ( x )
(6) 0的平方根和立方根都是0 ( √ )
归纳:平方等于本身的数:
立方等于本身的数:
平方根等于本身的数:
算术平方根等于本身的数:
立方根等于本身的数:
立方根的表示方法
问:若有意义,求的取值范围?任意实数
【设计意图】通过类比平方根的定义,引导学生归纳得出立方根的定义,再通过计算求立方根的正反例判断,更利于学生结合实际例子理解立方根的定义,一题一总结,有利于培养学生观察,归纳,总结的能力.
(三)典例讲解
例1 求下列各数的立方根
(1) (2) (3) (4)
解(1)∵的立方根是,即
(2)∵,∴的立方根是即
(3)∵,∴的立方根是,即
(4)∵,∴的立方根是,即
例2说出下列各式的意义,并求它们的值
(1) (2) (3) (4)
解(1)729的立方根;
(2)的立方根的相反数;
(3)的立方根的相反数;
(4)的立方的立方根;
方法:求带分数的立方根应先化为假分数
例3.计算(1) (2)
(3). (4)
解(1)原式 (2)原式
原式 (4)原式
总结:平方根与立方根的区别和联系
【设计意图】通过上题练习让学生牢固掌握立方根的定义并能用定义求一个数的立方根,并理解立方根的表示方式,会表示一个数的立方根.
(四)针对训练
1.若=2,=4,求的值.
解:∵=2,=4,
∴,
∴
∴或
∴ == 4 或 ==0.
2.已知是的算术平方根,的立方根,求的值
解:∵ 由题意可得
∴
∵ ,
∴
∴
3.求未知数的值
(1) (2)
(3) (4)
解(1)∵
∴
解得:
(2)原方程变形为:
∵
∴
解得:
解(1)∵
∴
解得:
(2)原方程变形为:
∵
∴
解得:
【设计意图】通过练习让学生熟练地掌握立方根的定义并能用其解题,考查学生的综合解题能力.
(五)变式训练
1.【问题发现】(1)计算下列各式
①_____1_______; _____1_____.
②__________; __________.
③___________; __________;
(2)观察上面式子及其计算结果,你能得到什么结论?
结论:①如果被开方数互为相反数,那么它们的立方根也互为相反数即:
②被开方数大,其立方根大,被开方数小,其立方根小.
1.【知识应用】计算下列各式
① ② ③
解①
②
③
1.【知识迁移】(1)已知+,且的平方根是它本身,求xy的立方根
解:∵ 和互为相反数
∴,解得
∵的平方根是它本身
∴,解得
∴
易错易混辨析
若则
若则
1.【知识迁移】(2) 比较下列各组数的大小.
(1)与 (2)与 (3)与
解(1)法一:立方法
∵
∴
法二:估值法(夹逼法)
∵
∴
∴
法三:计算器
∵ 按键顺序:
∴
解(2)∵,
∴
(3)∵
∵
∴
【设计意图】通过此题一题多解发展学生的发散思维,并总结比较大小的两种常用方法:①平方法,②估值法. 发展学生估值的思维,养成估值的意识.
(六)拓展探究
1.已知的立方根是,的算术平方根是,是的整数部分,求的平方根.
解:∵的立方根是,的算术平方根是
∴
∴
∵
∴
∴
∴
∴
2.(1)计算下列各式的值,你能发现什么规律
规律:被开方数扩大(缩小)1000倍时,它的立方根扩大(缩小)10倍.
(2)利用(1)中的结论,如果,那么_13.33______
【设计意图】1题主要培养学生综合分析,综合运用和综合解题的能力,2题培养学生类比,观察,猜想,归纳的能力,并运用所得知识解决问题的能力.
(七)当堂检测
1.的立方根用符号表示,正确的是( C )
A. B. C. D.
2.有理数-8的立方根是( A )
A.-2 B.2 C.±2 D.±4
3.下列各组数中,互为相反数的一组是( A )
A.与 B. 与
C.与 D. 与
4.计算
(1)_____0.4_____;(2)______;
(3)____1_______;(4)_____ ______;
(5)的立方根是____-2______
(6)的平方根是________
(7)若则的值为__14____
(8)若,则的取值范围__m<2_____
(9)和之间的整数是 5 .
5.计算(1)
(2)
(3)
解(1)原式
(2)原式
(3)原式
6.求未知数的值
(1) (2)
解(1)原方程变形为:
∵
∴
解得:
(2)原方程变形为:
∵
∴解得:
7.已知的平方根是±3,的立方根是2,求的算术平方根
解:∵的平方根是±3
∴即
∵的立方根是2
∴
∴
∴
8.已知和互为相反数,求的值.
解:根据题意,得
∴
∴
∴
【设计意图】针对本节课所学,巩固学生理解立方根的概念,会求一个数的立方根,会利用立方根解决问题,培养学生综合解题的能力.
(八)小结梳理
【设计意图】通过课堂小结,使学生对本节课的知识有一个系统的回顾和认识,进而形成一个清晰的脉络,加深学生对本节课知识的理解与掌握.
(九)布置作业
必做题P49.练习1,2,3,选做题P51练习8,9题.
五、教学反思
21世纪教育网(www.21cnjy.com)
同课章节目录
