【2025春新教材】人教版七年级下册数学8.3 实数及其简单运算(第1课时 实数概念) 课件(共34张PPT)
文档属性
| 名称 | 【2025春新教材】人教版七年级下册数学8.3 实数及其简单运算(第1课时 实数概念) 课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 00:00:00 | ||
图片预览








文档简介
(共34张PPT)
8.3实数及其简单运算
第1课时 实数概念
第8章 实数
人教版(新教材)数学七年级下册
1.理解实数的意义,并能将实数按要求进行准确的分类;
2.理解实数和数轴上的点一一对应,能用数轴上的点表示无理数;
3. 掌握利用数轴比较实数大小.
核
心
素
养
目
标
目录
CONTENT
情景引入
1
合作探究
2
典例分析
3
巩固练习
4
归纳总结
5
感受中考
6
小结梳理
7
布置作业
8
问题导入
问1 我们知道有理数包括整数和分数,把下列分数写成小数的形式.
问2:整数能写成小数的形式吗?例如:5
问3.这些小数它们有什么特征?
有限小数和无限循环小数
整数可以写成小数点后为0的小数
问题导入
有理数:有限小数或无限循环小数。
任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
新知讲解
问4.所有的数都可以写成有限小数和无限循环小数的形式吗?
不是.如:
(两个1之间依次多一个0)
问5.这些小数它们又有什么特征?
无限不循环
新知讲解
无理数的概念
无限不循环小数叫做无理数.
常见的无理数类型
(1) 含有的数;如,
(2) 开不尽方的数开方所得结果;如
(3) 有规律但不循环的小数,如 1.01001000100001…
新知应用
1.下列实数是无理数的是( )
A. B.1 C.0 D.-5
2.判断下列数是有理数还是无理数
①;②;③;④;⑤;⑥;
A
有理数
无理数
无理数
有理数
有理数
有理数
注意
(1)类似①带根号的数不一定是无理数,带根号时还应注意根指数,
(2)类似⑤⑥先化简再判断
新知应用
3.下列各数是有理数还是无理数?
(1) (2) (3) (4)(每相邻两个2之间依次多一个0) (5) (6) (7) (8) (9) (10)
有理数集合
无理数集合
...
...
新知讲解
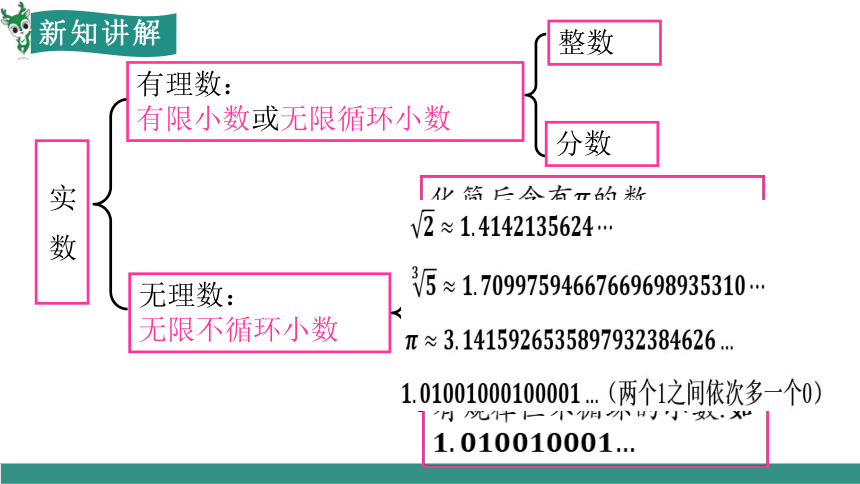
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
分数
整数
化简后含开方开不尽的数.如
有规律但不循环的小数.如
化简后含有的数.
如
新知讲解
问6.我们将有理数和无理数统称为实数,仿照有理数的分类吗?据此你能给出实数的其它分类吗?
无理数
有理数
实 数
负有理数
正有理数
正无理数:
负无理数:
有限小数或无限循环小数
无限不循环小数
0
按定义划分
新知讲解
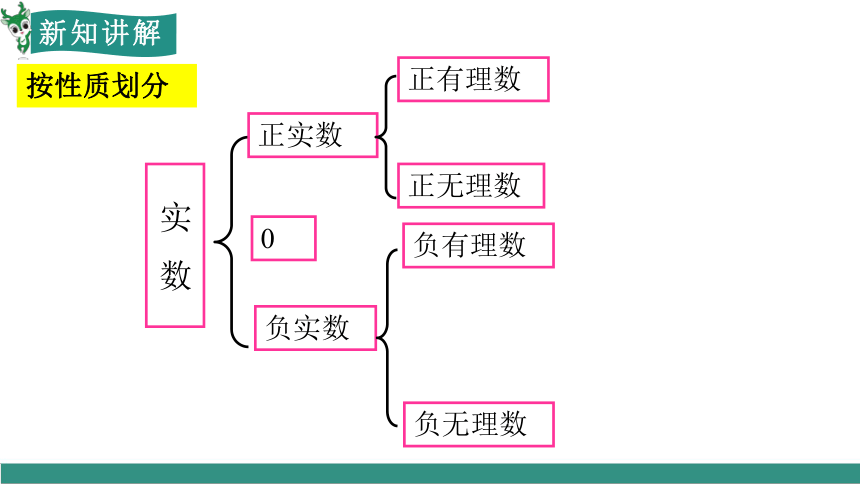
负实数
正实数
实 数
正无理数
正有理数
负有理数
负无理数
0
按性质划分
典例讲解
例1 将下列各数分别填入下列相应的括号内:
,,,,,,,0,
(每两个3之间依次多一个7)
无理数集合:{ …};
有理数集合:{ …};
正实数集合:{ …};
负实数集合:{ …}.
,,,
,,,,0
,,
,,,,
对每个数都要进行判断,分类标准不同结果不同.
针对训练
1.判断:
(1).实数不是有理数就是无理数。( )
(2).实数分为正实数和负实数。( )
(3).无理数都是无限不循环小数。( )
(4).无理数都是无限小数。( )
(5).带根号的数都是无理数。( )
(6).无理数一定都带根号。( )
×
×
×
针对训练
2.将下列各数分别填入下列相应的括号内
,-3,,,,,,,
正实数集合:{ …};
非正数集合:{ …};
正分数集合:{ …};
自然数集合:{ …};
无理数集合:{ …}.
,,
,,,,,
,
,
新知探究
问7.每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点来表示呢?
思考1: 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则数轴上表示点A的数是多少?
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
●
A
∵圆的周长为,∴点A所对的数为:
新知探究
思考2:你能在数轴上表示出和吗?
1
1
1
(1)把两个边长为1的小正方形通过剪、拼,得到一个大正方形,大正方形的边长为 ,从而说明边长为1的小正方形的对角线为 .
新知探究
(2)如下图,以一个单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
-2
-1
1
2
B
A
C
1
1
O
∵OA=OB=0C,∴ 点A所对的数为:,点B所对的数为:.
新知探究
数轴上的点有些表示有理数,有些表示无理数.
每一个无理数都可以用数轴上的一个点来表示出来。
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数。
实数与数轴上的点是一一对应的
典例讲解
例2.如图所示,数轴上A,B两点表示的数分别为和,
(1)点B关于原点O的对称点为E,求点E所表示的实数
解:(1)∵数轴上B两点表示的数分别为,
∴点B到原点0的距离为,
则点E到原点的距离为,
∴点E表示的实数为,
典例讲解
例2.如图所示,数轴上A,B两点表示的数分别为和,
(2)点B关于点A的对称点为C,求点C所表示的实数.
解:(2)法一
∵数轴上A,B两点表示的数分别为和,
∴点B到点A的距离为,则点C到点A的距离为,
设点C表示的实数为,则点A到点C的距离为,
∴,
∴
当点C为点B关于点A的对称点时,CA=BA
数轴上两点间的距离的求法:
数轴上两点间的距离等于表示这两点的数之差的绝对值.
典例讲解
例2.如图所示,数轴上A,B两点表示的数分别为和,
(2)点B关于点A的对称点为C,求点C所表示的实数.
解:(2)法二
设点C表示的实数为
∵点B关于点A的对称点为C,即A为BC的中点
∴,
∴
中点公式:若为的中点,点所表示的数为点所表示的数为,则中点点所表示的数为:
典例讲解
例3.(1)请将数轴上是各点与下列实数对应起来:
-3 -2 -1 0 1 2 3 4
A
B
C
D
E
(2)比较它们的大小(用“<”号连接)
在数轴上表示的两个实数,右边的数总比左边的数大。
典例讲解
原点
0
正实数
负实数
与有理数一样,在实数范围内:
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
4.数轴上的点越往右表示的实数越大
针对训练
1.如图,数轴上表示实数的点可能是( )
A.点P B.点Q C.点R D.点S
B
2.如图,在数轴上点A和点B之间表示整数的点有 个
3.小于的所有正整数有_____________________.
4.数轴上表示的对应点为A,B,点B关于点A的对称点为C,则点C所表示的数是________
4
,,,
(第1题图)
(第2题图)
当堂检测
1.下列实数中是无理数的是( )
A. B. C. D.
2.下列说法:①无限小数是无理数;②开方开不尽的实数都是无理数;③有理数都是实数;④所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数;⑤是分数.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
C
B
新知讲解
3.如图所示,数轴上A,B两点表示的数分别为和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
C
4.如图,数轴上的点A、B、O、C、D分别表示数,,,,,则表示数的点P应落在( )
A.线段AB上 B.线段BO上
C.线段OC上 D.线段CD上
B
(第3题图)
(第4题图)
当堂检测
5.点A在数轴上表示的数为,点B在数轴上表示的数为,则A,B两点之间的距离为________.
6.如图,在数轴上点A表示的数是.若把点A向左平移2个单位得到点B,则点B表示的数是__________;再作点B关于原点0的对称点C,则点C表示的数是_________
当堂检测
7.把下列各数填入相应的集合内.
,,,,,,
有理数集合:{ …};
无理数集合:{ …};
正实数集合:{ …};
负实数集合:{ …}.
,,,,
,,
,,,
,,
当堂检测
8.把下列各数近似地表示在数轴上,并用“<”把它们连接起来.
, ,,,, .
解析∴
小结梳理
无理数:
无限不循环小数
有理数:有限小数或无限循环小数
数 实
化简后含开方开不尽的数.如
有规律但不循环的小数.如
化简后含有的数.
如
轴 数
一一对应
布置作业
作业:P54第1,2,3题
谢谢观看
8.3实数及其简单运算
第1课时 实数概念
第8章 实数
人教版(新教材)数学七年级下册
1.理解实数的意义,并能将实数按要求进行准确的分类;
2.理解实数和数轴上的点一一对应,能用数轴上的点表示无理数;
3. 掌握利用数轴比较实数大小.
核
心
素
养
目
标
目录
CONTENT
情景引入
1
合作探究
2
典例分析
3
巩固练习
4
归纳总结
5
感受中考
6
小结梳理
7
布置作业
8
问题导入
问1 我们知道有理数包括整数和分数,把下列分数写成小数的形式.
问2:整数能写成小数的形式吗?例如:5
问3.这些小数它们有什么特征?
有限小数和无限循环小数
整数可以写成小数点后为0的小数
问题导入
有理数:有限小数或无限循环小数。
任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
新知讲解
问4.所有的数都可以写成有限小数和无限循环小数的形式吗?
不是.如:
(两个1之间依次多一个0)
问5.这些小数它们又有什么特征?
无限不循环
新知讲解
无理数的概念
无限不循环小数叫做无理数.
常见的无理数类型
(1) 含有的数;如,
(2) 开不尽方的数开方所得结果;如
(3) 有规律但不循环的小数,如 1.01001000100001…
新知应用
1.下列实数是无理数的是( )
A. B.1 C.0 D.-5
2.判断下列数是有理数还是无理数
①;②;③;④;⑤;⑥;
A
有理数
无理数
无理数
有理数
有理数
有理数
注意
(1)类似①带根号的数不一定是无理数,带根号时还应注意根指数,
(2)类似⑤⑥先化简再判断
新知应用
3.下列各数是有理数还是无理数?
(1) (2) (3) (4)(每相邻两个2之间依次多一个0) (5) (6) (7) (8) (9) (10)
有理数集合
无理数集合
...
...
新知讲解
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
分数
整数
化简后含开方开不尽的数.如
有规律但不循环的小数.如
化简后含有的数.
如
新知讲解
问6.我们将有理数和无理数统称为实数,仿照有理数的分类吗?据此你能给出实数的其它分类吗?
无理数
有理数
实 数
负有理数
正有理数
正无理数:
负无理数:
有限小数或无限循环小数
无限不循环小数
0
按定义划分
新知讲解
负实数
正实数
实 数
正无理数
正有理数
负有理数
负无理数
0
按性质划分
典例讲解
例1 将下列各数分别填入下列相应的括号内:
,,,,,,,0,
(每两个3之间依次多一个7)
无理数集合:{ …};
有理数集合:{ …};
正实数集合:{ …};
负实数集合:{ …}.
,,,
,,,,0
,,
,,,,
对每个数都要进行判断,分类标准不同结果不同.
针对训练
1.判断:
(1).实数不是有理数就是无理数。( )
(2).实数分为正实数和负实数。( )
(3).无理数都是无限不循环小数。( )
(4).无理数都是无限小数。( )
(5).带根号的数都是无理数。( )
(6).无理数一定都带根号。( )
×
×
×
针对训练
2.将下列各数分别填入下列相应的括号内
,-3,,,,,,,
正实数集合:{ …};
非正数集合:{ …};
正分数集合:{ …};
自然数集合:{ …};
无理数集合:{ …}.
,,
,,,,,
,
,
新知探究
问7.每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点来表示呢?
思考1: 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则数轴上表示点A的数是多少?
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
●
A
∵圆的周长为,∴点A所对的数为:
新知探究
思考2:你能在数轴上表示出和吗?
1
1
1
(1)把两个边长为1的小正方形通过剪、拼,得到一个大正方形,大正方形的边长为 ,从而说明边长为1的小正方形的对角线为 .
新知探究
(2)如下图,以一个单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
-2
-1
1
2
B
A
C
1
1
O
∵OA=OB=0C,∴ 点A所对的数为:,点B所对的数为:.
新知探究
数轴上的点有些表示有理数,有些表示无理数.
每一个无理数都可以用数轴上的一个点来表示出来。
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数。
实数与数轴上的点是一一对应的
典例讲解
例2.如图所示,数轴上A,B两点表示的数分别为和,
(1)点B关于原点O的对称点为E,求点E所表示的实数
解:(1)∵数轴上B两点表示的数分别为,
∴点B到原点0的距离为,
则点E到原点的距离为,
∴点E表示的实数为,
典例讲解
例2.如图所示,数轴上A,B两点表示的数分别为和,
(2)点B关于点A的对称点为C,求点C所表示的实数.
解:(2)法一
∵数轴上A,B两点表示的数分别为和,
∴点B到点A的距离为,则点C到点A的距离为,
设点C表示的实数为,则点A到点C的距离为,
∴,
∴
当点C为点B关于点A的对称点时,CA=BA
数轴上两点间的距离的求法:
数轴上两点间的距离等于表示这两点的数之差的绝对值.
典例讲解
例2.如图所示,数轴上A,B两点表示的数分别为和,
(2)点B关于点A的对称点为C,求点C所表示的实数.
解:(2)法二
设点C表示的实数为
∵点B关于点A的对称点为C,即A为BC的中点
∴,
∴
中点公式:若为的中点,点所表示的数为点所表示的数为,则中点点所表示的数为:
典例讲解
例3.(1)请将数轴上是各点与下列实数对应起来:
-3 -2 -1 0 1 2 3 4
A
B
C
D
E
(2)比较它们的大小(用“<”号连接)
在数轴上表示的两个实数,右边的数总比左边的数大。
典例讲解
原点
0
正实数
负实数
与有理数一样,在实数范围内:
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
4.数轴上的点越往右表示的实数越大
针对训练
1.如图,数轴上表示实数的点可能是( )
A.点P B.点Q C.点R D.点S
B
2.如图,在数轴上点A和点B之间表示整数的点有 个
3.小于的所有正整数有_____________________.
4.数轴上表示的对应点为A,B,点B关于点A的对称点为C,则点C所表示的数是________
4
,,,
(第1题图)
(第2题图)
当堂检测
1.下列实数中是无理数的是( )
A. B. C. D.
2.下列说法:①无限小数是无理数;②开方开不尽的实数都是无理数;③有理数都是实数;④所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数;⑤是分数.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
C
B
新知讲解
3.如图所示,数轴上A,B两点表示的数分别为和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
C
4.如图,数轴上的点A、B、O、C、D分别表示数,,,,,则表示数的点P应落在( )
A.线段AB上 B.线段BO上
C.线段OC上 D.线段CD上
B
(第3题图)
(第4题图)
当堂检测
5.点A在数轴上表示的数为,点B在数轴上表示的数为,则A,B两点之间的距离为________.
6.如图,在数轴上点A表示的数是.若把点A向左平移2个单位得到点B,则点B表示的数是__________;再作点B关于原点0的对称点C,则点C表示的数是_________
当堂检测
7.把下列各数填入相应的集合内.
,,,,,,
有理数集合:{ …};
无理数集合:{ …};
正实数集合:{ …};
负实数集合:{ …}.
,,,,
,,
,,,
,,
当堂检测
8.把下列各数近似地表示在数轴上,并用“<”把它们连接起来.
, ,,,, .
解析∴
小结梳理
无理数:
无限不循环小数
有理数:有限小数或无限循环小数
数 实
化简后含开方开不尽的数.如
有规律但不循环的小数.如
化简后含有的数.
如
轴 数
一一对应
布置作业
作业:P54第1,2,3题
谢谢观看
同课章节目录
