第五章 轴对称与旋转(培优)(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章 轴对称与旋转(培优)
一、单选题
1.(2024九上·鹤山月考)2024年6月25日,嫦娥六号返回器准确着陆于预定区域,工作正常,标志着探月工程嫦娥六号任务取得圆满成功,实现世界首次月球背面采样返回.下列航天领域的图标中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.(2024九上·武汉期中)如图,将绕点顺时针旋转得到.若点在的延长线上,则的度数为( )
A. B. C. D.
3.(2024九上·浙江期末)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
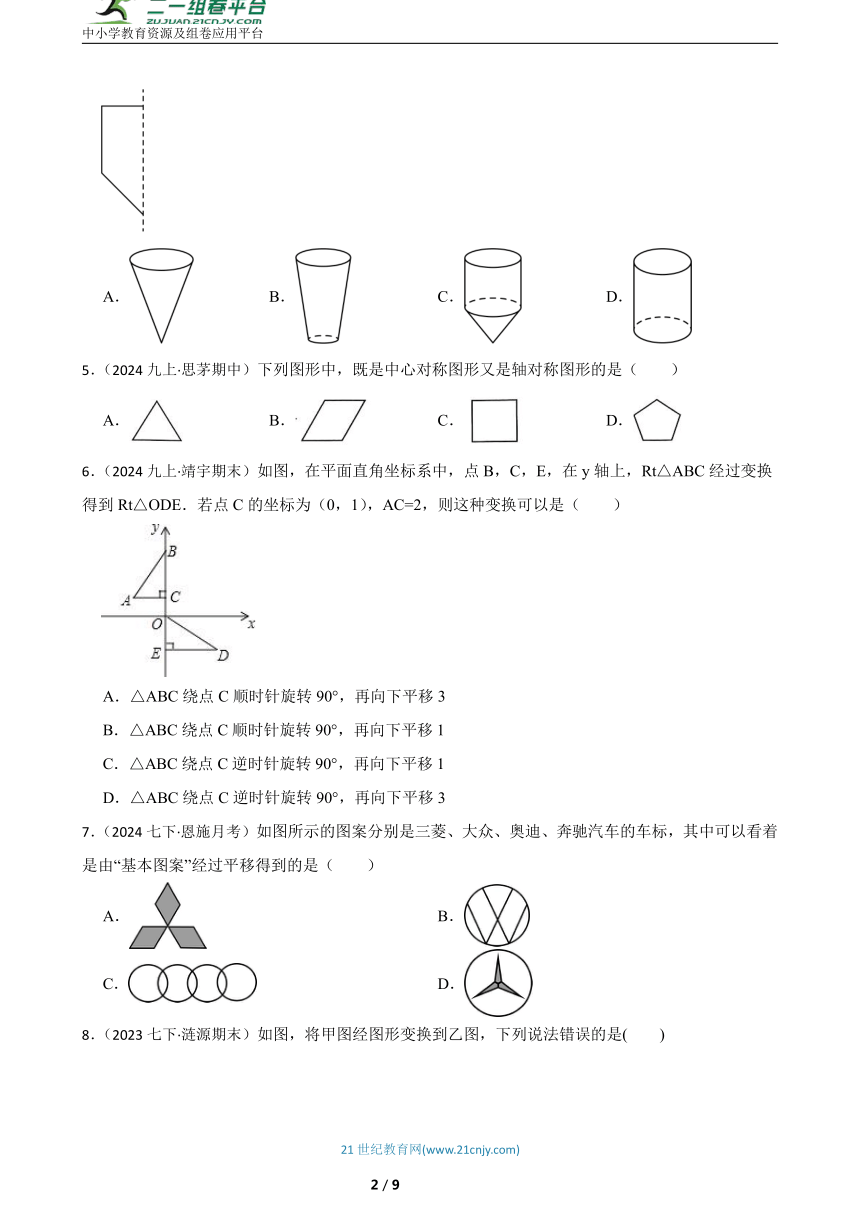
4.(2024七上·余江月考)如图所示的图形绕虚线旋转一周,可以得到的几何体是( )
A. B. C. D.
5.(2024九上·思茅期中)下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
6.(2024九上·靖宇期末)如图,在平面直角坐标系中,点B,C,E,在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
A.△ABC绕点C顺时针旋转90°,再向下平移3
B.△ABC绕点C顺时针旋转90°,再向下平移1
C.△ABC绕点C逆时针旋转90°,再向下平移1
D.△ABC绕点C逆时针旋转90°,再向下平移3
7.(2024七下·恩施月考)如图所示的图案分别是三菱、大众、奥迪、奔驰汽车的车标,其中可以看着是由“基本图案”经过平移得到的是( )
A. B.
C. D.
8.(2023七下·涟源期末)如图,将甲图经图形变换到乙图,下列说法错误的是( )
A.可以通过平移和旋转实现 B.可以通过轴对称和旋转实现
C.必须通过旋转才能实现 D.不必通过璇转就能实现
9.(2023七下·南山期中)下列说法中正确的是( )
A.两条直线被第三条直线所截,内错角相等;
B.在同一平面内,垂直于同一条直线的两条直线平行;
C.直线外一点到这条直线的垂线段叫做点到直线的距离;
D.在同一平面内不重合的两条直线有平行、相交和垂直三种位置关系.
10.(2024九上·越秀期末)如图,将绕点逆时针方向旋转得到,若点恰好落在边上,则的度数是( ).
A. B. C. D.
二、填空题
11.(2024九下·杨浦模拟)在四张完全相同的卡片上,分别画有:正三角形、正八边形、圆和矩形.如果从中任意抽取1张卡片,那么这张卡片上所画图形既是轴对称图形又是中心对称图形的概率是 .
12.(2024八下·罗湖期中)如图,将绕着点顺时针旋转得到,若,,则旋转角等于 .
13.(2024七下·周口期末)如图,线段可以看成是线段先绕点C 旋转,再向 平移 小格得到的.
14.(2023九上·诸暨月考)如图,将绕着点O顺时针旋转得到,若,则旋转角度是 .
15.(2024九上·浦东期中)国际奥委会会旗上的图案由5个圆环组成.每两个圆环相交的部分叫做曲边四边形,如图所示,从左至右共有8个曲边四边形,分别给它们标上序号.观察图形,我们发现标号为2的曲边四边形(下简称“2”)经过平移能与“6”重合,2还与 成轴对称.(请把能成轴对称的曲边四边形标号都填上)
16.(2024·柳州模拟)如图,将一块含角的三角板绕点A按逆时针方向旋转到的位置.若,则旋转的角度为 .
三、计算题
17.(2024七上·佛山月考)两张长方形纸片如图1、图2所示,小容将图1长方形纸片卷起来从而得到一个圆柱体;小易将图2长方形纸片绕其一条边所在直线旋转一周,从而得到一个圆柱体.请你通过计算判断哪位同学得到的圆柱体体积大(取3).
四、解答题
18.(2024九上·沾益月考)图中的图形均可以由“基本图案”通过变换得到.(填序号)
(1)通过平移变换但不能通过旋转变换得到的图案是__;
(2)可以通过旋转变换但不能通过平移变换得到的图案是__;
(3)既可以由平移变换,也可以由旋转变换得到的图案是__.
19.(2023九上·浙江期中)如图,在平面直角坐标系中,各顶点的坐标分别为.
(1)将绕点逆时针旋转后对应得到,请写出点的坐标.
(2)请在图中画出绕点顺时针旋转后的,并求出旋转过程中点所经过的路径长(结果保留根号和).
20.(2024八下·徐州期末)如图,在方格纸中建立平面直角坐标系,与的顶点均为格点.
(1)若绕点逆时针旋转可得到,则旋转角至少为______;
(2)将绕点顺时针旋转得到,画出;
(3)若(2)中的与成中心对称,则对称中心的坐标为______.
21.(2023七上·巴中月考)将一副直角三角板按如图1 摆放在直线AD 上(直角三角板OBC 和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC 不动,将三角板MON 绕点O 以每秒8°的速度顺时针方向旋转t 秒.
(1)如图2,当t= 秒时,OM 平分∠AOC,此时∠NOC﹣∠AOM= ;
(2)继续旋转三角板MON,如图3,使得OM、ON 同时在直线OC 的右侧,猜想∠NOC与∠AOM 有怎样的数量关系?并说明理由(数量关系中不能含t);
(3)直线AD 的位置不变,若在三角板MON 开始顺时针旋转的同时,另一个三角板OBC也绕点O 以每秒2°的速度顺时针旋转,当OM 旋转至射线OD 上时,两个三角板同时停止运动.
①当t= 秒时,∠MOC=15°;
②请直接写出在旋转过程中,∠NOC 与∠AOM 的数量关系(数量关系中不能含t).
答案解析部分
1.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
2.【答案】C
【知识点】三角形内角和定理;等腰三角形的性质;旋转的性质
3.【答案】C
【知识点】轴对称图形
4.【答案】C
【知识点】图形的旋转
5.【答案】C
【知识点】轴对称图形;中心对称及中心对称图形
6.【答案】A
【知识点】图形的旋转;图形的平移
7.【答案】C
【知识点】利用轴对称设计图案;利用平移设计图案;利用旋转设计图案
8.【答案】D
【知识点】利用轴对称设计图案;利用旋转设计图案;图形的平移
9.【答案】B
【知识点】点到直线的距离;平行线的判定;平行线的性质;平面中直线位置关系
10.【答案】A
【知识点】三角形内角和定理;等腰三角形的性质;旋转的性质
11.【答案】
【知识点】轴对称图形;中心对称及中心对称图形
12.【答案】
【知识点】旋转的性质
13.【答案】逆时针;左;1
【知识点】旋转的性质;利用旋转设计图案;图形的平移
14.【答案】50°
【知识点】角的运算;图形的旋转
15.【答案】3,7
【知识点】轴对称的性质;图形的平移
16.【答案】
【知识点】角的运算;旋转的性质
17.【答案】小易同学将图2长方形纸片绕的边旋转时得到的圆柱体体积大
【知识点】图形的旋转;已知展开图进行几何体的相关的计算
18.【答案】(1)①④;(2) ②⑤;(3) ③
【知识点】旋转的性质;利用旋转设计图案;图形的平移
19.【答案】(1)解:如图,
由题意可得,点,,;
即为所求.
(2)解:由勾股定理得,,
∴旋转过程中点所经过的路径长为.
【知识点】勾股定理;弧长的计算;作图﹣旋转;尺规作图-作三角形
20.【答案】(1)
(2)
(3)
【知识点】点的坐标;旋转的性质;作图﹣旋转;两个图形成中心对称
21.【答案】(1)2.8125;45°
(2)解:∠NOC-∠AOM =45°
(3)①∵∠AOB=2t,∠AOM=8t,
∴∠AOC=45°+2t,
∴45°+2t-8t=15°或8t-45°-2t=15°.
解得t=5或10.
②∠NOC-∠AOM=15°.
∵∠AOB=2t,∠AOM=8t,∠MON=90°,∠BOC=45°,
∵∠AON=90°+∠AOM=90°+8t,∠AOC=∠AOB+∠BOC=45°+2t,
∴∠NOC=∠AON-∠AOC=90°+8t-45°-2t=45°+6t,
∴∠NOC-∠AOM=15°.
【知识点】角的运算;图形的旋转;角平分线的概念
21世纪教育网(www.21cnjy.com)
1 / 9
第五章 轴对称与旋转(培优)
一、单选题
1.(2024九上·鹤山月考)2024年6月25日,嫦娥六号返回器准确着陆于预定区域,工作正常,标志着探月工程嫦娥六号任务取得圆满成功,实现世界首次月球背面采样返回.下列航天领域的图标中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.(2024九上·武汉期中)如图,将绕点顺时针旋转得到.若点在的延长线上,则的度数为( )
A. B. C. D.
3.(2024九上·浙江期末)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4.(2024七上·余江月考)如图所示的图形绕虚线旋转一周,可以得到的几何体是( )
A. B. C. D.
5.(2024九上·思茅期中)下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
6.(2024九上·靖宇期末)如图,在平面直角坐标系中,点B,C,E,在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
A.△ABC绕点C顺时针旋转90°,再向下平移3
B.△ABC绕点C顺时针旋转90°,再向下平移1
C.△ABC绕点C逆时针旋转90°,再向下平移1
D.△ABC绕点C逆时针旋转90°,再向下平移3
7.(2024七下·恩施月考)如图所示的图案分别是三菱、大众、奥迪、奔驰汽车的车标,其中可以看着是由“基本图案”经过平移得到的是( )
A. B.
C. D.
8.(2023七下·涟源期末)如图,将甲图经图形变换到乙图,下列说法错误的是( )
A.可以通过平移和旋转实现 B.可以通过轴对称和旋转实现
C.必须通过旋转才能实现 D.不必通过璇转就能实现
9.(2023七下·南山期中)下列说法中正确的是( )
A.两条直线被第三条直线所截,内错角相等;
B.在同一平面内,垂直于同一条直线的两条直线平行;
C.直线外一点到这条直线的垂线段叫做点到直线的距离;
D.在同一平面内不重合的两条直线有平行、相交和垂直三种位置关系.
10.(2024九上·越秀期末)如图,将绕点逆时针方向旋转得到,若点恰好落在边上,则的度数是( ).
A. B. C. D.
二、填空题
11.(2024九下·杨浦模拟)在四张完全相同的卡片上,分别画有:正三角形、正八边形、圆和矩形.如果从中任意抽取1张卡片,那么这张卡片上所画图形既是轴对称图形又是中心对称图形的概率是 .
12.(2024八下·罗湖期中)如图,将绕着点顺时针旋转得到,若,,则旋转角等于 .
13.(2024七下·周口期末)如图,线段可以看成是线段先绕点C 旋转,再向 平移 小格得到的.
14.(2023九上·诸暨月考)如图,将绕着点O顺时针旋转得到,若,则旋转角度是 .
15.(2024九上·浦东期中)国际奥委会会旗上的图案由5个圆环组成.每两个圆环相交的部分叫做曲边四边形,如图所示,从左至右共有8个曲边四边形,分别给它们标上序号.观察图形,我们发现标号为2的曲边四边形(下简称“2”)经过平移能与“6”重合,2还与 成轴对称.(请把能成轴对称的曲边四边形标号都填上)
16.(2024·柳州模拟)如图,将一块含角的三角板绕点A按逆时针方向旋转到的位置.若,则旋转的角度为 .
三、计算题
17.(2024七上·佛山月考)两张长方形纸片如图1、图2所示,小容将图1长方形纸片卷起来从而得到一个圆柱体;小易将图2长方形纸片绕其一条边所在直线旋转一周,从而得到一个圆柱体.请你通过计算判断哪位同学得到的圆柱体体积大(取3).
四、解答题
18.(2024九上·沾益月考)图中的图形均可以由“基本图案”通过变换得到.(填序号)
(1)通过平移变换但不能通过旋转变换得到的图案是__;
(2)可以通过旋转变换但不能通过平移变换得到的图案是__;
(3)既可以由平移变换,也可以由旋转变换得到的图案是__.
19.(2023九上·浙江期中)如图,在平面直角坐标系中,各顶点的坐标分别为.
(1)将绕点逆时针旋转后对应得到,请写出点的坐标.
(2)请在图中画出绕点顺时针旋转后的,并求出旋转过程中点所经过的路径长(结果保留根号和).
20.(2024八下·徐州期末)如图,在方格纸中建立平面直角坐标系,与的顶点均为格点.
(1)若绕点逆时针旋转可得到,则旋转角至少为______;
(2)将绕点顺时针旋转得到,画出;
(3)若(2)中的与成中心对称,则对称中心的坐标为______.
21.(2023七上·巴中月考)将一副直角三角板按如图1 摆放在直线AD 上(直角三角板OBC 和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC 不动,将三角板MON 绕点O 以每秒8°的速度顺时针方向旋转t 秒.
(1)如图2,当t= 秒时,OM 平分∠AOC,此时∠NOC﹣∠AOM= ;
(2)继续旋转三角板MON,如图3,使得OM、ON 同时在直线OC 的右侧,猜想∠NOC与∠AOM 有怎样的数量关系?并说明理由(数量关系中不能含t);
(3)直线AD 的位置不变,若在三角板MON 开始顺时针旋转的同时,另一个三角板OBC也绕点O 以每秒2°的速度顺时针旋转,当OM 旋转至射线OD 上时,两个三角板同时停止运动.
①当t= 秒时,∠MOC=15°;
②请直接写出在旋转过程中,∠NOC 与∠AOM 的数量关系(数量关系中不能含t).
答案解析部分
1.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
2.【答案】C
【知识点】三角形内角和定理;等腰三角形的性质;旋转的性质
3.【答案】C
【知识点】轴对称图形
4.【答案】C
【知识点】图形的旋转
5.【答案】C
【知识点】轴对称图形;中心对称及中心对称图形
6.【答案】A
【知识点】图形的旋转;图形的平移
7.【答案】C
【知识点】利用轴对称设计图案;利用平移设计图案;利用旋转设计图案
8.【答案】D
【知识点】利用轴对称设计图案;利用旋转设计图案;图形的平移
9.【答案】B
【知识点】点到直线的距离;平行线的判定;平行线的性质;平面中直线位置关系
10.【答案】A
【知识点】三角形内角和定理;等腰三角形的性质;旋转的性质
11.【答案】
【知识点】轴对称图形;中心对称及中心对称图形
12.【答案】
【知识点】旋转的性质
13.【答案】逆时针;左;1
【知识点】旋转的性质;利用旋转设计图案;图形的平移
14.【答案】50°
【知识点】角的运算;图形的旋转
15.【答案】3,7
【知识点】轴对称的性质;图形的平移
16.【答案】
【知识点】角的运算;旋转的性质
17.【答案】小易同学将图2长方形纸片绕的边旋转时得到的圆柱体体积大
【知识点】图形的旋转;已知展开图进行几何体的相关的计算
18.【答案】(1)①④;(2) ②⑤;(3) ③
【知识点】旋转的性质;利用旋转设计图案;图形的平移
19.【答案】(1)解:如图,
由题意可得,点,,;
即为所求.
(2)解:由勾股定理得,,
∴旋转过程中点所经过的路径长为.
【知识点】勾股定理;弧长的计算;作图﹣旋转;尺规作图-作三角形
20.【答案】(1)
(2)
(3)
【知识点】点的坐标;旋转的性质;作图﹣旋转;两个图形成中心对称
21.【答案】(1)2.8125;45°
(2)解:∠NOC-∠AOM =45°
(3)①∵∠AOB=2t,∠AOM=8t,
∴∠AOC=45°+2t,
∴45°+2t-8t=15°或8t-45°-2t=15°.
解得t=5或10.
②∠NOC-∠AOM=15°.
∵∠AOB=2t,∠AOM=8t,∠MON=90°,∠BOC=45°,
∵∠AON=90°+∠AOM=90°+8t,∠AOC=∠AOB+∠BOC=45°+2t,
∴∠NOC=∠AON-∠AOC=90°+8t-45°-2t=45°+6t,
∴∠NOC-∠AOM=15°.
【知识点】角的运算;图形的旋转;角平分线的概念
21世纪教育网(www.21cnjy.com)
1 / 9
同课章节目录
