辽宁省抚顺市六校协作体2024-2025学年高一上学期期末数学试卷(PDF版,含答案)
文档属性
| 名称 | 辽宁省抚顺市六校协作体2024-2025学年高一上学期期末数学试卷(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 689.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 11:29:03 | ||
图片预览



文档简介
辽宁省抚顺市六校协作体 2024-2025 学年高一上学期期末数学试卷
一、单选题:本题共 8 小题,每小题 5 分,共 40 分。在每小题给出的选项中,只有一项是符合题目要求的。
2 + , ≥ 0,
1.已知函数 ( ) = { ,则 ( ( 1)) =( )
| + 1| + 2, < 0.
A. 2 B. 0 C. 2 D. 6
2.若“存在 ∈ ,使得 2 + + 1 < 0”是假命题,则实数 的取值范围是( )
A. [ 2,+∞) B. ( ∞, 2] ∪ [2,+∞)
C. [ 2,2] D. ( 2,2)
3.已知 > > 0 > ,则下列不等式正确的是( )
1 1 3 3 1 1 A. < B. < C. 2 > 2 D. lg < 0
4.星等是天文学上对星星明暗程度的一种表示方法,可分为两种:目视星等与绝对星等.它们之间可用公式
= + 5 5 转换,其中 为绝对星等, 为目视星等, 为到地球的距离(单位:光年).现在地球某
3.26
处测得1号星的绝对星等为 1,目视星等为 1;2号星绝对星等为 2,目视星等为 2.则1号星与2号星到地
球的距离之比为( )
1+ 2 ( 1+ 2) 1 1 ( 2 2) ( 1 1)( 2 2) 1 1
A. 10 5 B. 10 5 C. 10 25 D. 10 2 2
1 2 2 1
5.已知集合 = { |( ) 2 > 1}, = { | ≤ 1},则 ∪ =( )
2 +1
A. [ 1,2] B. [ 2,2] C. ( 2,2] D. ( 1,2]
6.函数 ( ) = log (6 )在[0,2]上为减函数,则 的取值范围是( )
A. (0,1) B. (1,3) C. (1,3] D. [3,+∞)
7.已知函数 ( ) = ln( 2 + + )的部分图象如图所示,则 + 的值是( )
A. 1 B. 1 C. 5 D. 5
( ) ( )
8.已知函数 ( )定义域为 ,且 ( ) = 2 + 2,若对任意的1 < 1 < 2 < 2,都有
1 2 > 5成立,
1 2
则实数 的取值范围是( )
第 1 页,共 9 页
5 5 5
A. [0,+∞) B. [ , +∞) C. ( ,+∞) D. [ , +∞)
4 4 2
二、多选题:本题共 3 小题,共 18 分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法正确的是( )
A. 某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛,“至少一名男生”和“全是女生”是对
立事件
B. 数据13,27,24,12,14,30,15,17,19,23的70%分位数是23
C. 已知甲、乙两门高射炮同时向一目标开炮,若甲击中目标的概率为0.6,乙击中目标的概率为0.8,则目
标被击中的概率为0.44
D. 数据 1, 2,…, 20的平均数为2,方差为3,则数据3 1 + 5,3 2 + 5,…,3 20 + 5的平均数为11,方
差为27
10.已知幂函数 ( ) = ( 2 3) ( , ∈ ),则下列说法正确的是( )
A. 若 = 1,则 ( )在(0,+∞)上单调递减
B. 若 = + 1,则 ( )是奇函数
C. 函数 = 2 ( 1) + 1过定点(2,1)
D. 若 = 3,则 (5) + ( 4) < 0
11.已知定义在区间[ 4,6]上的函数 ( )满足:对任意 , ∈ 均有 ( + 1) + ( ) = ( );当 > 1
时, ( ) > 0.则下列说法正确的是( )
A. (1) = 0
B. ( )在定义域上单调递减
C. ( + 1)是奇函数
D. 若 (2) = 1,则不等式 (2 ) > ( ) + 2的解集为(2,3]
三、填空题:本题共 3 小题,每小题 5 分,共 15 分。
12.函数 = ( )满足:(1)定义域为 ;(2) ( ) = ( );(3)在( ∞, 0)上为增函数.请写出满足上述三个条
件的一个函数解析式______(答案不唯一,正确即可);
13.已知 ( )是奇函数,且当 < 0时, ( ) = 3 ,则 ( 2) = ______.
14.设[ ]表示不超过 的最大整数,如[1.5] = 1,[ 1.5] = 2.则函数 ( ) = 2 [ ] 1的零点为______.
四、解答题:本题共 5 小题,共 148 分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
已知集合 = { | 3 < 3 < 4}, = { |2 ≤ 2 2 ≤ 6}, = { | 1 ≤ ≤ + 2}.
第 2 页,共 9 页
(1)求 ∩ ( );
(2)若 ∈ 是 ∈ 的充分条件, ∈ 是 ∈ 的必要条件,求 的取值范围.
16.(本小题12分)
学校鼓励学生课余时间积极参加体育锻炼,每天能用于锻炼的课余时间有60分钟,现需要制定一个课余锻
炼考核评分制度,建立一个每天得分 与当天锻炼时间 (单位:分)的函数关系.要求及图示如下:(1)函数是
区间[0,60]上的增函数;(2)每天运动时间为0分钟时,当天得分为0分;(3)每天运动时间为20分钟时,当天
得分为3分;(4)每天最多得分不超过6分.现有以下三个函数模型供选择:① = + ( > 0),② =
1.2 + ( > 0),③ = 2( + 2) + ( > 0). 10
(1)请你根据函数图象性质从中选择一个合适的函数模型,不需要说明理由:
(2)根据所给信息求出函数的解析式;
(3)求每天得分不少于4.5分,至少需要锻炼多少分钟. (注:√ 2 ≈ 1.414,结果保留整数).
17.(本小题12分)
已知 > 0, > 0,且 + 2 = 2.
1 1
(1)求 + 的最小值:
(2)求3 + 9 的最小值;
4
(3)求 的最大值.
+1
18.(本小题100分)
2024年5月22日至5月28日是第二届全国城市生活垃圾分类宣传周,本次宣传周的主题为“践行新时尚分类
志愿行”.某中学高一年级举行了一次“垃圾分类知识竞赛”,为了了解本次竞赛成绩情况,从中抽取了部
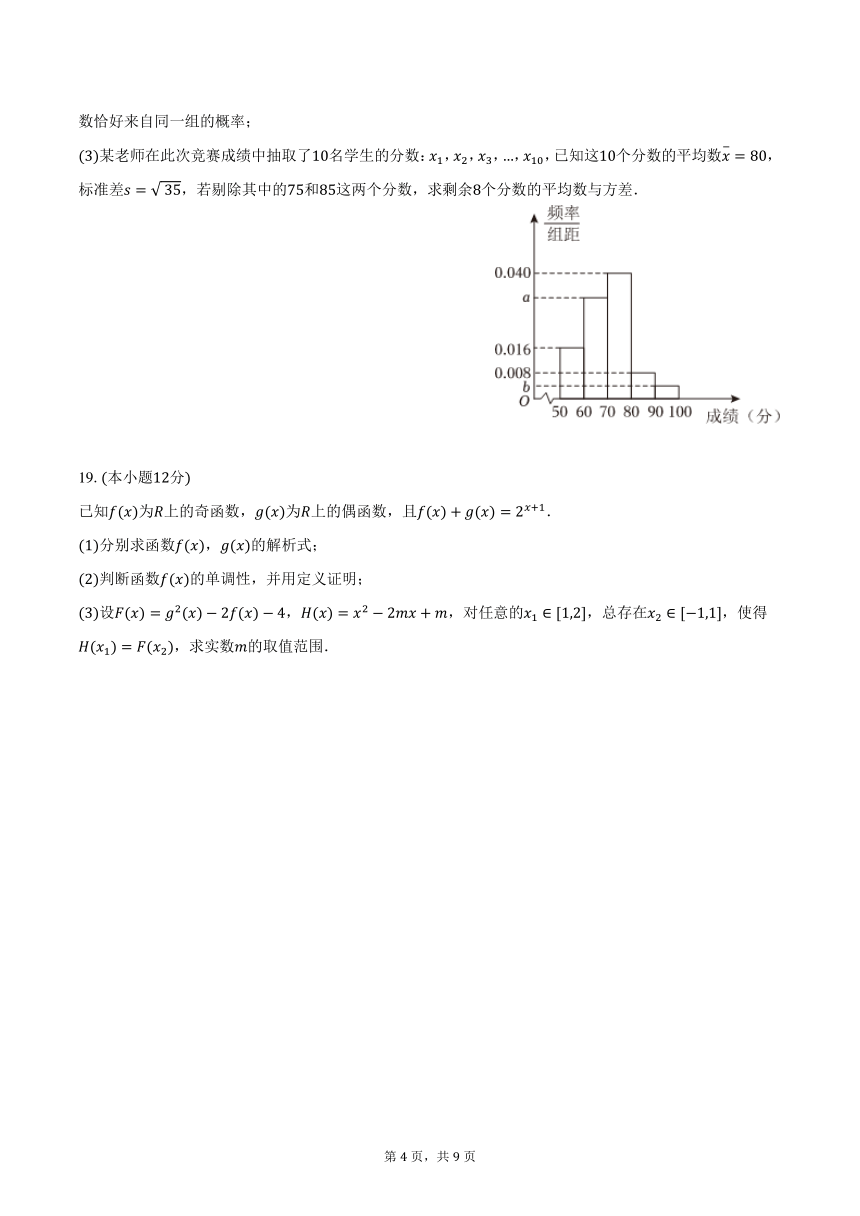
分学生的成绩 (单位:分,得分取正整数,满分为100分)作为样本进行统计,将成绩进行整理后,分为五
组(50 ≤ < 60,60 ≤ < 70,70 ≤ < 80,80 ≤ < 90,90 ≤ ≤ 100),其中第二组的频数是第一组频数的2
倍,请根据下面尚未完成的频率分布直方图(如图所示)解决下列问题:
(1)求 , 的值,并估计这次竞赛成绩的中位数(同一组中的数据用该组区间的中点值作代表);
(2)如果用分层抽样的方法从样本成绩为[80,90)和[90,100]的学生中共抽取6人,再从6人中选2人,求2人分
第 3 页,共 9 页
数恰好来自同一组的概率;
(3)某老师在此次竞赛成绩中抽取了10名学生的分数: 1, 2, 3,…, 10,已知这10个分数的平均数 = 80,
标准差 = √ 35,若剔除其中的75和85这两个分数,求剩余8个分数的平均数与方差.
19.(本小题12分)
已知 ( )为 上的奇函数, ( )为 上的偶函数,且 ( ) + ( ) = 2 +1.
(1)分别求函数 ( ), ( )的解析式;
(2)判断函数 ( )的单调性,并用定义证明;
(3)设 ( ) = 2( ) 2 ( ) 4, ( ) = 2 2 + ,对任意的 1 ∈ [1,2],总存在 2 ∈ [ 1,1],使得
( 1) = ( 2),求实数 的取值范围.
第 4 页,共 9 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】 = 2(答案不唯一)
1
13.【答案】
8
14.【答案】√ 2
15.【答案】解:(1)因为 = { |2 ≤ 2 2 ≤ 6} = { |2 ≤ ≤ 4},
所以 = { | < 2或 > 4},
又 = { | 3 < 3 < 4} = { | 1 < < 6},
所以 ∩ ( ) = { | 1 < < 2或4 < < 6}.
(2)若 ∈ 是 ∈ 的充分条件,则 ,
因为 = { | 1 ≤ ≤ + 2},
1 ≤ 2
所以{ ,解得2 ≤ ≤ 3,
+ 2 ≥ 4
若 ∈ 是 ∈ 的必要条件,则 ,
1 > 1
所以{ ,解得0 < < 4.
+ 2 < 6
综上, 的取值范围为{ |2 ≤ ≤ 3}.
16.【答案】解:(1)建立一个每天得分 与当天锻炼时间 (单位:分)的函数关系,
现有以下三个函数模型供选择:① = + ( > 0),② = 1.2 + ( > 0),③ = 2( + 2) +10
( > 0);
第 5 页,共 9 页
对于模型③ = 2( + 2) + ( > 0), 10
对数型的函数增长速度较慢,符合题意,故选项模型③;
(2)所求函数过点(0,0),(20,3),
22 + = 0
则{ 20 ,解得 = 3, = 3,
2( + 2) + = 310
故所求函数为 = 3 2( + 2) 3, 10
60
经检验,当 = 60时, = 3 2( + 2) 3 = 6,符合题意, 10
综上所述,函数的解析式为 = 3 2( + 2) 3; 10
5
(3) ∵每天得分不少于4.5分,∴ 3 2( + 2) 3 ≥ 4.5,即 ( + 2) ≥ , 10 2 10 2
5
∴ + 2 ≥ 22 = 4√ 2,即 ≥ 40√ 2 20 ≈ 40 × 1.414 20 = 36.56 ≈ 37,
10
∴每天得分不少于4.5分,至少需要锻炼37分钟.
1 1 1 1 1 1 2 1 2 3+2√ 2
17【. 答案】解:(1)因为 + 2 = 2,所以 + = ( + 2 )( + ) = ( + + 3) ≥ (3 + 2√ ) = ,
2 2 2 2
2
= = 2√ 2 2当且仅当{ 时,即{ 时等号成立,
+ 2 = 2 = 2 √ 2
1 1 2√ 2+3
所以 + 的最小值为 ;
2
(2)因为3 > 0,9 > 0,
所以3 + 9 = 3 + 32 ≥ 2√ 3 32 = 2√ 3 +2 = 6,
3 = 32 = 1当且仅当{ ,即{ 1时等号成立,
+ 2 = 2 = 2
所以3 + 9 的最小值6;
(3)因为 + 2 = 2,则 = 2 2 > 0,所以0 < < 1,
4 4 4 4 4
所以 = 2 2 = 2 [2( + 1) + 2] = 4 [2( + 1) + ] ≤ 4 2√ 2( + 1) =
+1 +1 +1 +1 +1
4 4√ 2,
4
= 4 2 2
当且仅当{2( + 1) = √ +1,即{ 时,取等号,
+ 2 = 2 = √ 2 1
4
所以 的最大值为4 4√ 2.
+1
18.【答案】解:(1)根据题意可得10 = 0.016 × 10 × 2,解得 = 0.032,
又(0.008 + 0.016 + 0.032 + 0.04 + ) × 10 = 1,解得 = 0.004,
第 6 页,共 9 页
因为前几组的频率依次为0.16,0.32,0.40,
所以中位数落在区间[70,80)内,
0.5 0.16 0.32
所以估计中位数为70 + = 70.5;
0.04
(2)第四组[80,90)的抽取人数为4,设所抽取的人为 , , , ,
第五组[90,100]的抽取人数为2,设所抽取的人为 , ,
则从中随机抽取两名学生有 , , , , , , , , , , , , , , ,共15种情
况,
记事件 =“抽取的两名学生在同一组”,所以事件 包含的基本事件为 , , , , , , ,
共7种情况.
7
所以 ( ) = ;
15
(3)由 = 80,得 1 + 2 + 3 + + 10 = 10 × 80 = 800,
2 1 2 又 = [( 1 ) + (
2
2 ) + + ( 10 )
2] = (√ 35)2 = 35,
10
所以( 1 )
2 + ( 2 )
2 + + ( )210 = 350,
剔除其中的75和85两个分数,设剩余8个数为 1, 2, 3,…, 7, 8,
平均数与标准差分别为 0, 0,
+ + + 800 75 85
则剩余8个分数的平均数: = 1 2 80 = = 80 = ; 8 8
2 所以( 1 ) + ( 2 )
2 + ( 2 28 ) + (75 80) + (85 80)
2 = 350,
即:( 2 21 ) + ( 2 ) + + ( 8 )
2 = 350 52 52 = 300.
1 1
方差: 2 20 = [( 1 ) + ( 2 )
2 + + ( 8 )
2] = × 300 = 37.5,
8 8
所以剩余8个分数的平均数为80,方差为37.5.
19.【答案】解:(1)因为 ( )为 上的奇函数, ( )为 上的偶函数,且 ( ) + ( ) = 2 +1①,
则 ( ) + ( ) = 2 +1,
所以 ( ) + ( ) = 2 +1②,
由① ②得到2 ( ) = 2 +1 2 +1,所以 ( ) = 2 2 ;
由①+②得到2 ( ) = 2 +1 + 2 +1,所以 ( ) = 2 + 2 ;
(2)单调递增,证明如下:
取任意 1, 2 ∈ ,且 1 < 2,
1 1
则 ( ) ( ) = 2 1 2 1 (2 2 2 2 11 2 ) = 2 2
2 + 2 1 2 2
第 7 页,共 9 页
2 1 2 2 1
= (2 1 2 2) + + = (2
1 2 2)(1 +
2 1 2 2 +
);
1 2
1
易知当 1 <
1 2
2时,2 2 < 0,1 + 2 +
> 0,
1 2
所以 ( 1) ( 2) < 0,
即 ( 1) < ( 2),
因此 ( )在 上单调递增;
(3)因为对任意的 1 ∈ [1,2],总存在 2 ∈ [ 1,1],使得 ( 1) = ( 2),
所以 ( )在[1,2]上的值域是 ( )在[ 1,1]上值域的子集.
设 ( )在[1,2]上的值域为集合 ,
3 3因为 ( ) = 2 2 是增函数,故 ∈ [ 1,1]时, ( ) ∈ [ , ],
2 2
令 = ( ) = 2 2
3 3
∈ [ , ],
2 2
则 2( ) = (2 + 2 )2 = (2 2 )2 + 4 = 2 + 4,
21
所以 ( ) = 2 2 ∈ [ 1, ],
4
21
所以 [ 1, ],
4
函数 ( ) = 2 2 + 的对称轴为 = ,开口向上,
①当 < 1时, ( ) = (1) = 1 , ( ) = (2) = 4 3 ,
21
即 = [1 , 4 3 ] [ 1, ].
4
< 1 < 1
所以{1 ≥ 1
5
,即{ ≤ 2 ,解得 ∈ [ , 1).
21 5 12
4 3 ≤ ≥
4 12
当1 ≤ ≤ 2时, ( ) = ( ) =
2 + , (1) = 1 , (2) = 4 3 ,
1 ≤ ≤ 2
2 + ≥ 1
21
因为 [ 1, ],所以 21
4 1 ≤
,
4
21
{4 3 ≤ 4
√ 5+1
解得 ∈ [1, ].
2
当 > 2时, ( ) = (2) = 4 3 , ( ) = (1) = 1 ,
21
= [4 3 , 1 ] [ 1, ],
4
第 8 页,共 9 页
> 2
所以{4 3 ≥ 1,解得 ∈ .
21
1 ≤
4
5 √ 5+1
综上所述: ∈ [ , ].
12 2
第 9 页,共 9 页
一、单选题:本题共 8 小题,每小题 5 分,共 40 分。在每小题给出的选项中,只有一项是符合题目要求的。
2 + , ≥ 0,
1.已知函数 ( ) = { ,则 ( ( 1)) =( )
| + 1| + 2, < 0.
A. 2 B. 0 C. 2 D. 6
2.若“存在 ∈ ,使得 2 + + 1 < 0”是假命题,则实数 的取值范围是( )
A. [ 2,+∞) B. ( ∞, 2] ∪ [2,+∞)
C. [ 2,2] D. ( 2,2)
3.已知 > > 0 > ,则下列不等式正确的是( )
1 1 3 3 1 1 A. < B. < C. 2 > 2 D. lg < 0
4.星等是天文学上对星星明暗程度的一种表示方法,可分为两种:目视星等与绝对星等.它们之间可用公式
= + 5 5 转换,其中 为绝对星等, 为目视星等, 为到地球的距离(单位:光年).现在地球某
3.26
处测得1号星的绝对星等为 1,目视星等为 1;2号星绝对星等为 2,目视星等为 2.则1号星与2号星到地
球的距离之比为( )
1+ 2 ( 1+ 2) 1 1 ( 2 2) ( 1 1)( 2 2) 1 1
A. 10 5 B. 10 5 C. 10 25 D. 10 2 2
1 2 2 1
5.已知集合 = { |( ) 2 > 1}, = { | ≤ 1},则 ∪ =( )
2 +1
A. [ 1,2] B. [ 2,2] C. ( 2,2] D. ( 1,2]
6.函数 ( ) = log (6 )在[0,2]上为减函数,则 的取值范围是( )
A. (0,1) B. (1,3) C. (1,3] D. [3,+∞)
7.已知函数 ( ) = ln( 2 + + )的部分图象如图所示,则 + 的值是( )
A. 1 B. 1 C. 5 D. 5
( ) ( )
8.已知函数 ( )定义域为 ,且 ( ) = 2 + 2,若对任意的1 < 1 < 2 < 2,都有
1 2 > 5成立,
1 2
则实数 的取值范围是( )
第 1 页,共 9 页
5 5 5
A. [0,+∞) B. [ , +∞) C. ( ,+∞) D. [ , +∞)
4 4 2
二、多选题:本题共 3 小题,共 18 分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法正确的是( )
A. 某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛,“至少一名男生”和“全是女生”是对
立事件
B. 数据13,27,24,12,14,30,15,17,19,23的70%分位数是23
C. 已知甲、乙两门高射炮同时向一目标开炮,若甲击中目标的概率为0.6,乙击中目标的概率为0.8,则目
标被击中的概率为0.44
D. 数据 1, 2,…, 20的平均数为2,方差为3,则数据3 1 + 5,3 2 + 5,…,3 20 + 5的平均数为11,方
差为27
10.已知幂函数 ( ) = ( 2 3) ( , ∈ ),则下列说法正确的是( )
A. 若 = 1,则 ( )在(0,+∞)上单调递减
B. 若 = + 1,则 ( )是奇函数
C. 函数 = 2 ( 1) + 1过定点(2,1)
D. 若 = 3,则 (5) + ( 4) < 0
11.已知定义在区间[ 4,6]上的函数 ( )满足:对任意 , ∈ 均有 ( + 1) + ( ) = ( );当 > 1
时, ( ) > 0.则下列说法正确的是( )
A. (1) = 0
B. ( )在定义域上单调递减
C. ( + 1)是奇函数
D. 若 (2) = 1,则不等式 (2 ) > ( ) + 2的解集为(2,3]
三、填空题:本题共 3 小题,每小题 5 分,共 15 分。
12.函数 = ( )满足:(1)定义域为 ;(2) ( ) = ( );(3)在( ∞, 0)上为增函数.请写出满足上述三个条
件的一个函数解析式______(答案不唯一,正确即可);
13.已知 ( )是奇函数,且当 < 0时, ( ) = 3 ,则 ( 2) = ______.
14.设[ ]表示不超过 的最大整数,如[1.5] = 1,[ 1.5] = 2.则函数 ( ) = 2 [ ] 1的零点为______.
四、解答题:本题共 5 小题,共 148 分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
已知集合 = { | 3 < 3 < 4}, = { |2 ≤ 2 2 ≤ 6}, = { | 1 ≤ ≤ + 2}.
第 2 页,共 9 页
(1)求 ∩ ( );
(2)若 ∈ 是 ∈ 的充分条件, ∈ 是 ∈ 的必要条件,求 的取值范围.
16.(本小题12分)
学校鼓励学生课余时间积极参加体育锻炼,每天能用于锻炼的课余时间有60分钟,现需要制定一个课余锻
炼考核评分制度,建立一个每天得分 与当天锻炼时间 (单位:分)的函数关系.要求及图示如下:(1)函数是
区间[0,60]上的增函数;(2)每天运动时间为0分钟时,当天得分为0分;(3)每天运动时间为20分钟时,当天
得分为3分;(4)每天最多得分不超过6分.现有以下三个函数模型供选择:① = + ( > 0),② =
1.2 + ( > 0),③ = 2( + 2) + ( > 0). 10
(1)请你根据函数图象性质从中选择一个合适的函数模型,不需要说明理由:
(2)根据所给信息求出函数的解析式;
(3)求每天得分不少于4.5分,至少需要锻炼多少分钟. (注:√ 2 ≈ 1.414,结果保留整数).
17.(本小题12分)
已知 > 0, > 0,且 + 2 = 2.
1 1
(1)求 + 的最小值:
(2)求3 + 9 的最小值;
4
(3)求 的最大值.
+1
18.(本小题100分)
2024年5月22日至5月28日是第二届全国城市生活垃圾分类宣传周,本次宣传周的主题为“践行新时尚分类
志愿行”.某中学高一年级举行了一次“垃圾分类知识竞赛”,为了了解本次竞赛成绩情况,从中抽取了部
分学生的成绩 (单位:分,得分取正整数,满分为100分)作为样本进行统计,将成绩进行整理后,分为五
组(50 ≤ < 60,60 ≤ < 70,70 ≤ < 80,80 ≤ < 90,90 ≤ ≤ 100),其中第二组的频数是第一组频数的2
倍,请根据下面尚未完成的频率分布直方图(如图所示)解决下列问题:
(1)求 , 的值,并估计这次竞赛成绩的中位数(同一组中的数据用该组区间的中点值作代表);
(2)如果用分层抽样的方法从样本成绩为[80,90)和[90,100]的学生中共抽取6人,再从6人中选2人,求2人分
第 3 页,共 9 页
数恰好来自同一组的概率;
(3)某老师在此次竞赛成绩中抽取了10名学生的分数: 1, 2, 3,…, 10,已知这10个分数的平均数 = 80,
标准差 = √ 35,若剔除其中的75和85这两个分数,求剩余8个分数的平均数与方差.
19.(本小题12分)
已知 ( )为 上的奇函数, ( )为 上的偶函数,且 ( ) + ( ) = 2 +1.
(1)分别求函数 ( ), ( )的解析式;
(2)判断函数 ( )的单调性,并用定义证明;
(3)设 ( ) = 2( ) 2 ( ) 4, ( ) = 2 2 + ,对任意的 1 ∈ [1,2],总存在 2 ∈ [ 1,1],使得
( 1) = ( 2),求实数 的取值范围.
第 4 页,共 9 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】 = 2(答案不唯一)
1
13.【答案】
8
14.【答案】√ 2
15.【答案】解:(1)因为 = { |2 ≤ 2 2 ≤ 6} = { |2 ≤ ≤ 4},
所以 = { | < 2或 > 4},
又 = { | 3 < 3 < 4} = { | 1 < < 6},
所以 ∩ ( ) = { | 1 < < 2或4 < < 6}.
(2)若 ∈ 是 ∈ 的充分条件,则 ,
因为 = { | 1 ≤ ≤ + 2},
1 ≤ 2
所以{ ,解得2 ≤ ≤ 3,
+ 2 ≥ 4
若 ∈ 是 ∈ 的必要条件,则 ,
1 > 1
所以{ ,解得0 < < 4.
+ 2 < 6
综上, 的取值范围为{ |2 ≤ ≤ 3}.
16.【答案】解:(1)建立一个每天得分 与当天锻炼时间 (单位:分)的函数关系,
现有以下三个函数模型供选择:① = + ( > 0),② = 1.2 + ( > 0),③ = 2( + 2) +10
( > 0);
第 5 页,共 9 页
对于模型③ = 2( + 2) + ( > 0), 10
对数型的函数增长速度较慢,符合题意,故选项模型③;
(2)所求函数过点(0,0),(20,3),
22 + = 0
则{ 20 ,解得 = 3, = 3,
2( + 2) + = 310
故所求函数为 = 3 2( + 2) 3, 10
60
经检验,当 = 60时, = 3 2( + 2) 3 = 6,符合题意, 10
综上所述,函数的解析式为 = 3 2( + 2) 3; 10
5
(3) ∵每天得分不少于4.5分,∴ 3 2( + 2) 3 ≥ 4.5,即 ( + 2) ≥ , 10 2 10 2
5
∴ + 2 ≥ 22 = 4√ 2,即 ≥ 40√ 2 20 ≈ 40 × 1.414 20 = 36.56 ≈ 37,
10
∴每天得分不少于4.5分,至少需要锻炼37分钟.
1 1 1 1 1 1 2 1 2 3+2√ 2
17【. 答案】解:(1)因为 + 2 = 2,所以 + = ( + 2 )( + ) = ( + + 3) ≥ (3 + 2√ ) = ,
2 2 2 2
2
= = 2√ 2 2当且仅当{ 时,即{ 时等号成立,
+ 2 = 2 = 2 √ 2
1 1 2√ 2+3
所以 + 的最小值为 ;
2
(2)因为3 > 0,9 > 0,
所以3 + 9 = 3 + 32 ≥ 2√ 3 32 = 2√ 3 +2 = 6,
3 = 32 = 1当且仅当{ ,即{ 1时等号成立,
+ 2 = 2 = 2
所以3 + 9 的最小值6;
(3)因为 + 2 = 2,则 = 2 2 > 0,所以0 < < 1,
4 4 4 4 4
所以 = 2 2 = 2 [2( + 1) + 2] = 4 [2( + 1) + ] ≤ 4 2√ 2( + 1) =
+1 +1 +1 +1 +1
4 4√ 2,
4
= 4 2 2
当且仅当{2( + 1) = √ +1,即{ 时,取等号,
+ 2 = 2 = √ 2 1
4
所以 的最大值为4 4√ 2.
+1
18.【答案】解:(1)根据题意可得10 = 0.016 × 10 × 2,解得 = 0.032,
又(0.008 + 0.016 + 0.032 + 0.04 + ) × 10 = 1,解得 = 0.004,
第 6 页,共 9 页
因为前几组的频率依次为0.16,0.32,0.40,
所以中位数落在区间[70,80)内,
0.5 0.16 0.32
所以估计中位数为70 + = 70.5;
0.04
(2)第四组[80,90)的抽取人数为4,设所抽取的人为 , , , ,
第五组[90,100]的抽取人数为2,设所抽取的人为 , ,
则从中随机抽取两名学生有 , , , , , , , , , , , , , , ,共15种情
况,
记事件 =“抽取的两名学生在同一组”,所以事件 包含的基本事件为 , , , , , , ,
共7种情况.
7
所以 ( ) = ;
15
(3)由 = 80,得 1 + 2 + 3 + + 10 = 10 × 80 = 800,
2 1 2 又 = [( 1 ) + (
2
2 ) + + ( 10 )
2] = (√ 35)2 = 35,
10
所以( 1 )
2 + ( 2 )
2 + + ( )210 = 350,
剔除其中的75和85两个分数,设剩余8个数为 1, 2, 3,…, 7, 8,
平均数与标准差分别为 0, 0,
+ + + 800 75 85
则剩余8个分数的平均数: = 1 2 80 = = 80 = ; 8 8
2 所以( 1 ) + ( 2 )
2 + ( 2 28 ) + (75 80) + (85 80)
2 = 350,
即:( 2 21 ) + ( 2 ) + + ( 8 )
2 = 350 52 52 = 300.
1 1
方差: 2 20 = [( 1 ) + ( 2 )
2 + + ( 8 )
2] = × 300 = 37.5,
8 8
所以剩余8个分数的平均数为80,方差为37.5.
19.【答案】解:(1)因为 ( )为 上的奇函数, ( )为 上的偶函数,且 ( ) + ( ) = 2 +1①,
则 ( ) + ( ) = 2 +1,
所以 ( ) + ( ) = 2 +1②,
由① ②得到2 ( ) = 2 +1 2 +1,所以 ( ) = 2 2 ;
由①+②得到2 ( ) = 2 +1 + 2 +1,所以 ( ) = 2 + 2 ;
(2)单调递增,证明如下:
取任意 1, 2 ∈ ,且 1 < 2,
1 1
则 ( ) ( ) = 2 1 2 1 (2 2 2 2 11 2 ) = 2 2
2 + 2 1 2 2
第 7 页,共 9 页
2 1 2 2 1
= (2 1 2 2) + + = (2
1 2 2)(1 +
2 1 2 2 +
);
1 2
1
易知当 1 <
1 2
2时,2 2 < 0,1 + 2 +
> 0,
1 2
所以 ( 1) ( 2) < 0,
即 ( 1) < ( 2),
因此 ( )在 上单调递增;
(3)因为对任意的 1 ∈ [1,2],总存在 2 ∈ [ 1,1],使得 ( 1) = ( 2),
所以 ( )在[1,2]上的值域是 ( )在[ 1,1]上值域的子集.
设 ( )在[1,2]上的值域为集合 ,
3 3因为 ( ) = 2 2 是增函数,故 ∈ [ 1,1]时, ( ) ∈ [ , ],
2 2
令 = ( ) = 2 2
3 3
∈ [ , ],
2 2
则 2( ) = (2 + 2 )2 = (2 2 )2 + 4 = 2 + 4,
21
所以 ( ) = 2 2 ∈ [ 1, ],
4
21
所以 [ 1, ],
4
函数 ( ) = 2 2 + 的对称轴为 = ,开口向上,
①当 < 1时, ( ) = (1) = 1 , ( ) = (2) = 4 3 ,
21
即 = [1 , 4 3 ] [ 1, ].
4
< 1 < 1
所以{1 ≥ 1
5
,即{ ≤ 2 ,解得 ∈ [ , 1).
21 5 12
4 3 ≤ ≥
4 12
当1 ≤ ≤ 2时, ( ) = ( ) =
2 + , (1) = 1 , (2) = 4 3 ,
1 ≤ ≤ 2
2 + ≥ 1
21
因为 [ 1, ],所以 21
4 1 ≤
,
4
21
{4 3 ≤ 4
√ 5+1
解得 ∈ [1, ].
2
当 > 2时, ( ) = (2) = 4 3 , ( ) = (1) = 1 ,
21
= [4 3 , 1 ] [ 1, ],
4
第 8 页,共 9 页
> 2
所以{4 3 ≥ 1,解得 ∈ .
21
1 ≤
4
5 √ 5+1
综上所述: ∈ [ , ].
12 2
第 9 页,共 9 页
同课章节目录
