湖北省恩施州高中教育联盟2024-2025学年高一年级上期末考试数学试题(PDF版,含答案)
文档属性
| 名称 | 湖北省恩施州高中教育联盟2024-2025学年高一年级上期末考试数学试题(PDF版,含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 403.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 00:00:00 | ||
图片预览



文档简介
湖北省恩施州高中教育联盟2024-2025学年高一年级上期末考试数学试题
第I卷(选择题)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.设集合,,则( )
A. B. C. D.
2.设命题,,则的否定为( )
A. , B. ,
C. , D. ,
3.已知,,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4.已知关于的不等式的解集为,则关于的不等式的解集为( )
A. B.
C. D.
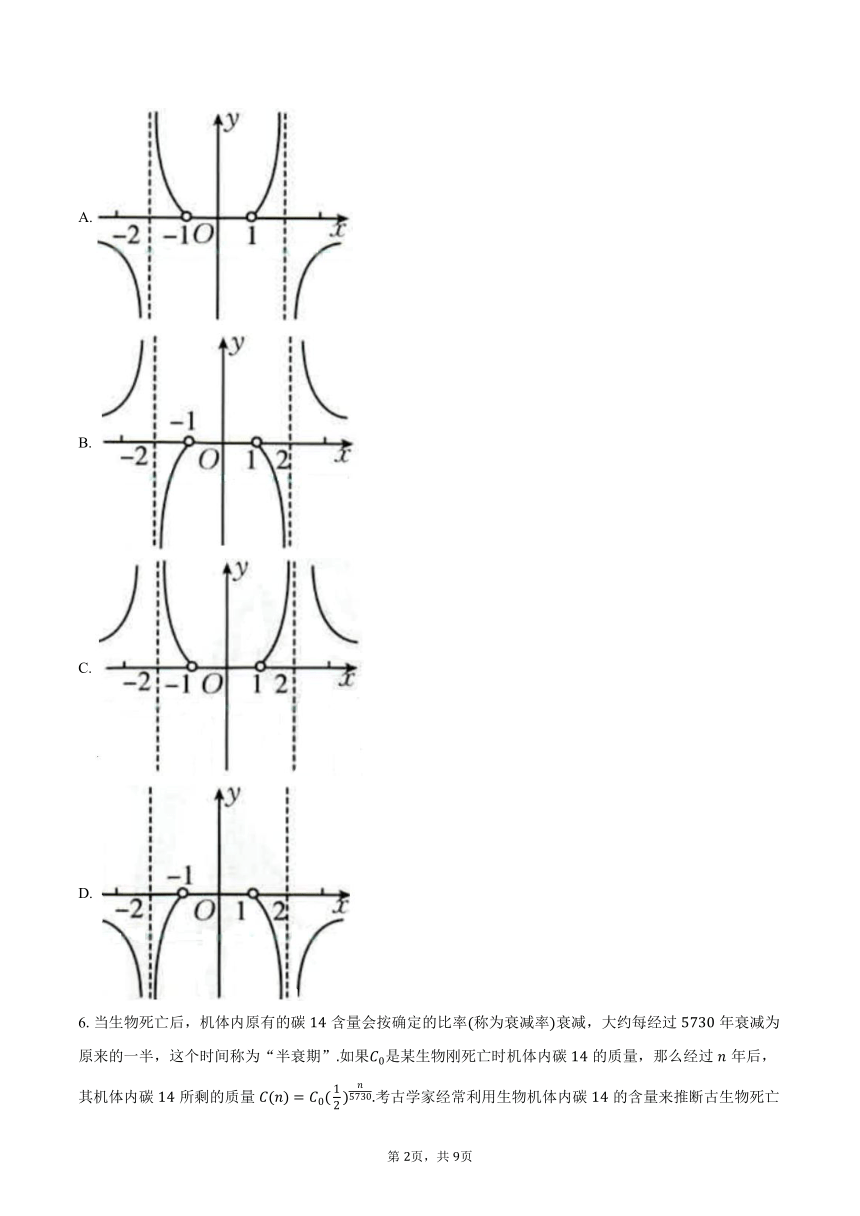
5.已知函数,则函数的大致图象是( )
A.
B.
C.
D.
6.当生物死亡后,机体内原有的碳含量会按确定的比率称为衰减率衰减,大约每经过年衰减为原来的一半,这个时间称为“半衰期”如果是某生物刚死亡时机体内碳的质量,那么经过年后,其机体内碳所剩的质量考古学家经常利用生物机体内碳的含量来推断古生物死亡的大致时间现考古发现某生物机体内碳的含量是刚死亡时的,根据以上知识推断该生物的死亡时间距今约 参考数据:,
A. 年 B. 年 C. 年 D. 年
7.已知函数的定义域为,,,,当时,恒有若,,,则,,的大小关系是( )
A. B. C. D.
8.已知函数且,,且,,则实数的取值范围是( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列选项正确的是( )
A.
B. 若扇形的圆心角为,弧长为,则该扇形的面积为
C. 若是第二象限角,则是第一或第四象限角
D. 若,则
10.已知函数,则下列选项正确的是( )
A. ,
B. 若方程有两个不等实根,则
C. 若方程有四个不等实根,,,,则
D. 方程所有实数根的和为
11.已知函数,,则下列选项正确的是( )
A. 若,则函数的最小值为
B. 若,且,则
C. 函数的图象关于点中心对称
D. 若,,是的三边,则
第II卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分。
12.函数称为函数,表示不超过实数的最大整数,例如:,若函数,则 .
13.已知是圆心在原点,半径为的圆上一点,点从开始,在圆上按逆时针方向做匀速圆周运动,角速度为,则时点的坐标为 .
14.正实数,满足,则的最小值为
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
若,求的值
计算:.
16.本小题分
已知.
若,求的值
已知的三个内角分别为,,,且,若,求的值.
17.本小题分
已知函数.
若函数的定义域为,求实数的取值范围
当时,判断函数在区间上的零点个数并证明.
18.本小题分
矩形的周长为,设.
求矩形面积的最大值及此时的值
当矩形为正方形时,将矩形分割成如图所示的四个全等的直角三角形和一个正方形,若正方形的边长为,求
若,如图,把矩形沿某条直线折叠,使得,重合,记为,折叠后,折痕与原矩形边,分别交于点,,的面积为,求的最小值.
19.本小题分
中国桥梁建筑的奇迹四渡河大桥位于湖北省恩施土家族苗族自治州巴东县,该桥主桥是一座特大单跨双铰钢桁架加劲梁悬索桥,两座桥墩之间的钢索构成的曲线形态在数学上被称为悬链线,悬链线在建筑和工程等领域有着广泛的应用悬链线是生活中常见的一种曲线,如沾满露珠自然下垂的蜘蛛丝、两根电线杆之间的电线、横跨深涧的观光索道的电缆等,这类悬链线对应的函数表达式为是非零常数,无理数
当,时,悬链线对应的函数又称为双曲正弦函数,记为当时,悬链线对应的函数又称为双曲余弦函数,记为求证:.
若为偶函数且在上单调递增,请写出一组符合条件的,的值,并说明理由.
在的条件下,关于的不等式的解集,求实数的取值范围.
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】解:,
,
,
;
原式
.
16.【答案】解:.
因为,所以,
.
因为的三个内角分别为,,,所以,
所以,即,
又因为,所以,
所以.
17.【答案】解:显然当,即时,不符合题意,所以,
要使的定义域为,则对于函数,
则,
解得,
所以实数的取值范围为.
在区间上有唯一一个零点,证明如下:
当时,,
令,所以函数在区间上单调递增.
又因为在区间上单调递增,
所以在区间上单调递增,
而,又,,所以,
而,又,
,,所以,
所以,
所以,结合在区间上单调递增.
所以在区间上有唯一一个零点.
18.【答案】解:设,由题意,,,,
所以矩形的面积,当且仅当时,等号成立,
所以矩形面积的最大值为,此时.
设,,由题意,,
即,又,
所以,,
所以.
因为,所以,设,,
所以,即,
易知直线过矩形中心,所以梯形的面积为,
所以,
所以
,
当且仅当,即时,等号成立.
故的最小值为.
19.【答案】解:证明:由题意,,,
所以
,证毕
因为为偶函数,所以,,
即,
所以,,所以,即,
此时,任取,且,
所以,
因为,所以,,,
所以,所以,
要使在上单调递增,
则,可以取答案不唯一
由可知,,,
所以原不等式可化为
,
又因为是单调递增的函数,且,
所以原不等式可化为,
由题意,,即,
当时,上式恒成立,即不等式的解集为,不符合题意
当时,解得,
即不等式的解集,
因为,所以,
所以或,
所以实数的取值范围为
第1页,共1页
第I卷(选择题)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.设集合,,则( )
A. B. C. D.
2.设命题,,则的否定为( )
A. , B. ,
C. , D. ,
3.已知,,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4.已知关于的不等式的解集为,则关于的不等式的解集为( )
A. B.
C. D.
5.已知函数,则函数的大致图象是( )
A.
B.
C.
D.
6.当生物死亡后,机体内原有的碳含量会按确定的比率称为衰减率衰减,大约每经过年衰减为原来的一半,这个时间称为“半衰期”如果是某生物刚死亡时机体内碳的质量,那么经过年后,其机体内碳所剩的质量考古学家经常利用生物机体内碳的含量来推断古生物死亡的大致时间现考古发现某生物机体内碳的含量是刚死亡时的,根据以上知识推断该生物的死亡时间距今约 参考数据:,
A. 年 B. 年 C. 年 D. 年
7.已知函数的定义域为,,,,当时,恒有若,,,则,,的大小关系是( )
A. B. C. D.
8.已知函数且,,且,,则实数的取值范围是( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列选项正确的是( )
A.
B. 若扇形的圆心角为,弧长为,则该扇形的面积为
C. 若是第二象限角,则是第一或第四象限角
D. 若,则
10.已知函数,则下列选项正确的是( )
A. ,
B. 若方程有两个不等实根,则
C. 若方程有四个不等实根,,,,则
D. 方程所有实数根的和为
11.已知函数,,则下列选项正确的是( )
A. 若,则函数的最小值为
B. 若,且,则
C. 函数的图象关于点中心对称
D. 若,,是的三边,则
第II卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分。
12.函数称为函数,表示不超过实数的最大整数,例如:,若函数,则 .
13.已知是圆心在原点,半径为的圆上一点,点从开始,在圆上按逆时针方向做匀速圆周运动,角速度为,则时点的坐标为 .
14.正实数,满足,则的最小值为
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
若,求的值
计算:.
16.本小题分
已知.
若,求的值
已知的三个内角分别为,,,且,若,求的值.
17.本小题分
已知函数.
若函数的定义域为,求实数的取值范围
当时,判断函数在区间上的零点个数并证明.
18.本小题分
矩形的周长为,设.
求矩形面积的最大值及此时的值
当矩形为正方形时,将矩形分割成如图所示的四个全等的直角三角形和一个正方形,若正方形的边长为,求
若,如图,把矩形沿某条直线折叠,使得,重合,记为,折叠后,折痕与原矩形边,分别交于点,,的面积为,求的最小值.
19.本小题分
中国桥梁建筑的奇迹四渡河大桥位于湖北省恩施土家族苗族自治州巴东县,该桥主桥是一座特大单跨双铰钢桁架加劲梁悬索桥,两座桥墩之间的钢索构成的曲线形态在数学上被称为悬链线,悬链线在建筑和工程等领域有着广泛的应用悬链线是生活中常见的一种曲线,如沾满露珠自然下垂的蜘蛛丝、两根电线杆之间的电线、横跨深涧的观光索道的电缆等,这类悬链线对应的函数表达式为是非零常数,无理数
当,时,悬链线对应的函数又称为双曲正弦函数,记为当时,悬链线对应的函数又称为双曲余弦函数,记为求证:.
若为偶函数且在上单调递增,请写出一组符合条件的,的值,并说明理由.
在的条件下,关于的不等式的解集,求实数的取值范围.
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】解:,
,
,
;
原式
.
16.【答案】解:.
因为,所以,
.
因为的三个内角分别为,,,所以,
所以,即,
又因为,所以,
所以.
17.【答案】解:显然当,即时,不符合题意,所以,
要使的定义域为,则对于函数,
则,
解得,
所以实数的取值范围为.
在区间上有唯一一个零点,证明如下:
当时,,
令,所以函数在区间上单调递增.
又因为在区间上单调递增,
所以在区间上单调递增,
而,又,,所以,
而,又,
,,所以,
所以,
所以,结合在区间上单调递增.
所以在区间上有唯一一个零点.
18.【答案】解:设,由题意,,,,
所以矩形的面积,当且仅当时,等号成立,
所以矩形面积的最大值为,此时.
设,,由题意,,
即,又,
所以,,
所以.
因为,所以,设,,
所以,即,
易知直线过矩形中心,所以梯形的面积为,
所以,
所以
,
当且仅当,即时,等号成立.
故的最小值为.
19.【答案】解:证明:由题意,,,
所以
,证毕
因为为偶函数,所以,,
即,
所以,,所以,即,
此时,任取,且,
所以,
因为,所以,,,
所以,所以,
要使在上单调递增,
则,可以取答案不唯一
由可知,,,
所以原不等式可化为
,
又因为是单调递增的函数,且,
所以原不等式可化为,
由题意,,即,
当时,上式恒成立,即不等式的解集为,不符合题意
当时,解得,
即不等式的解集,
因为,所以,
所以或,
所以实数的取值范围为
第1页,共1页
同课章节目录
