湘教版(2024)七下4.4.2 平行线的判定 同步探究学案
文档属性
| 名称 | 湘教版(2024)七下4.4.2 平行线的判定 同步探究学案 |  | |
| 格式 | docx | ||
| 文件大小 | 278.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-17 15:25:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
4.4.2 平行线的判定
学习目标与重难点
学习目标:
1.学习平行线判定方法2和判定方法3,并了解学习各方法在具体题目中的实际运用;
2.掌握平行线判定方法的推理证明过程,进一步学习推理,证明的方法、格式等;
3.通过简单的推理过程的学习,培养学生进行数学推理的习惯和方法,同时培养提高学生“观察-分析-推理-论证”的能力.
学习重点:平行线判定方法2和判定方法3的推理过程及几何解题的基本格式;
学习难点:判定定理的形成过程中的逻辑推理思路及用数学语言描述、书写的格式等.
预习自测
一、单选题
1.如图,要得到,则需要条件( )
A. B.
C. D.
二、填空题
2.把两块形状、大小相同的三角尺按照如图所示的样子放置,则,理由是 .
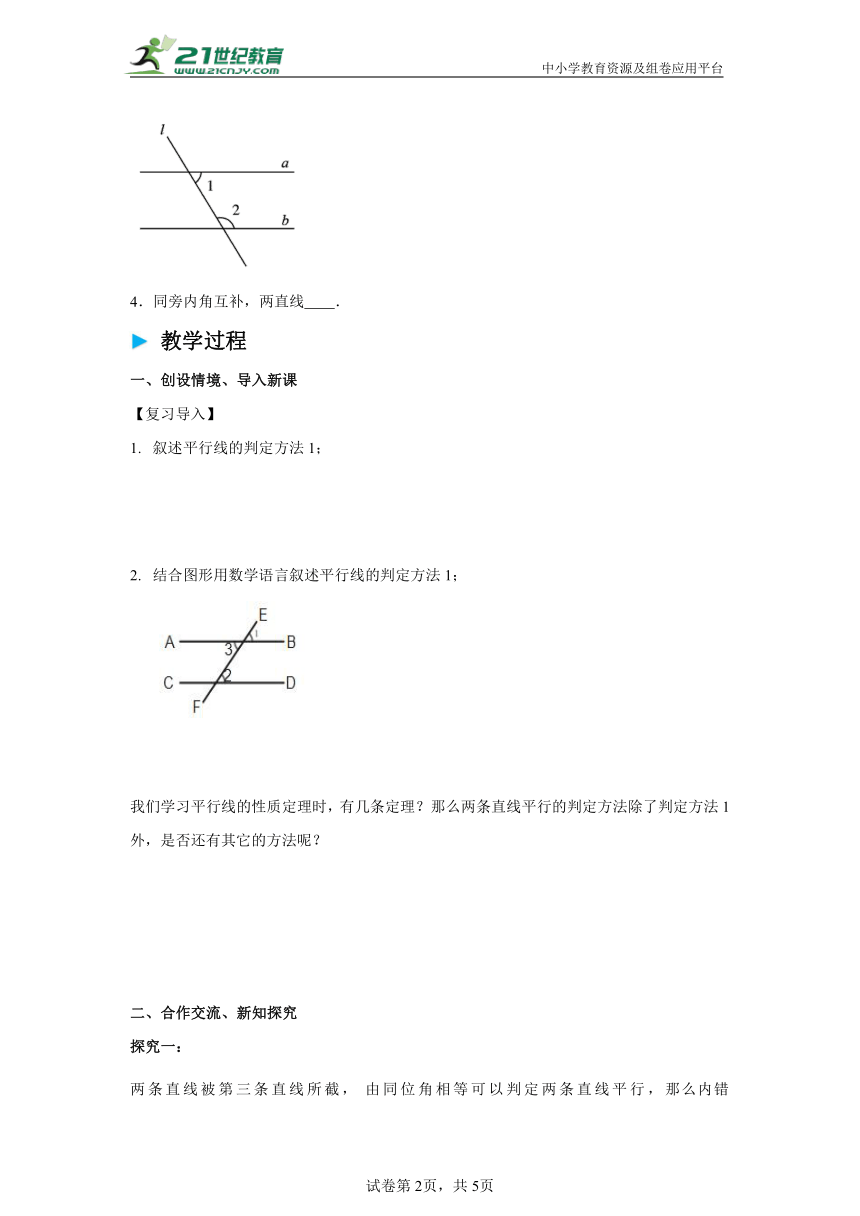
3.如图,已知直线分别与直线,相交,,那么与的位置关系是 .
4.同旁内角互补,两直线 .
教学过程
一、创设情境、导入新课
【复习导入】
叙述平行线的判定方法1;
结合图形用数学语言叙述平行线的判定方法1;
我们学习平行线的性质定理时,有几条定理?那么两条直线平行的判定方法除了判定方法1外,是否还有其它的方法呢?
二、合作交流、新知探究
探究一:
两条直线被第三条直线所截, 由同位角相等可以判定两条直线平行,那么内错角相等可以判定两条直线平行吗? 同旁内角互补呢?
探究二:
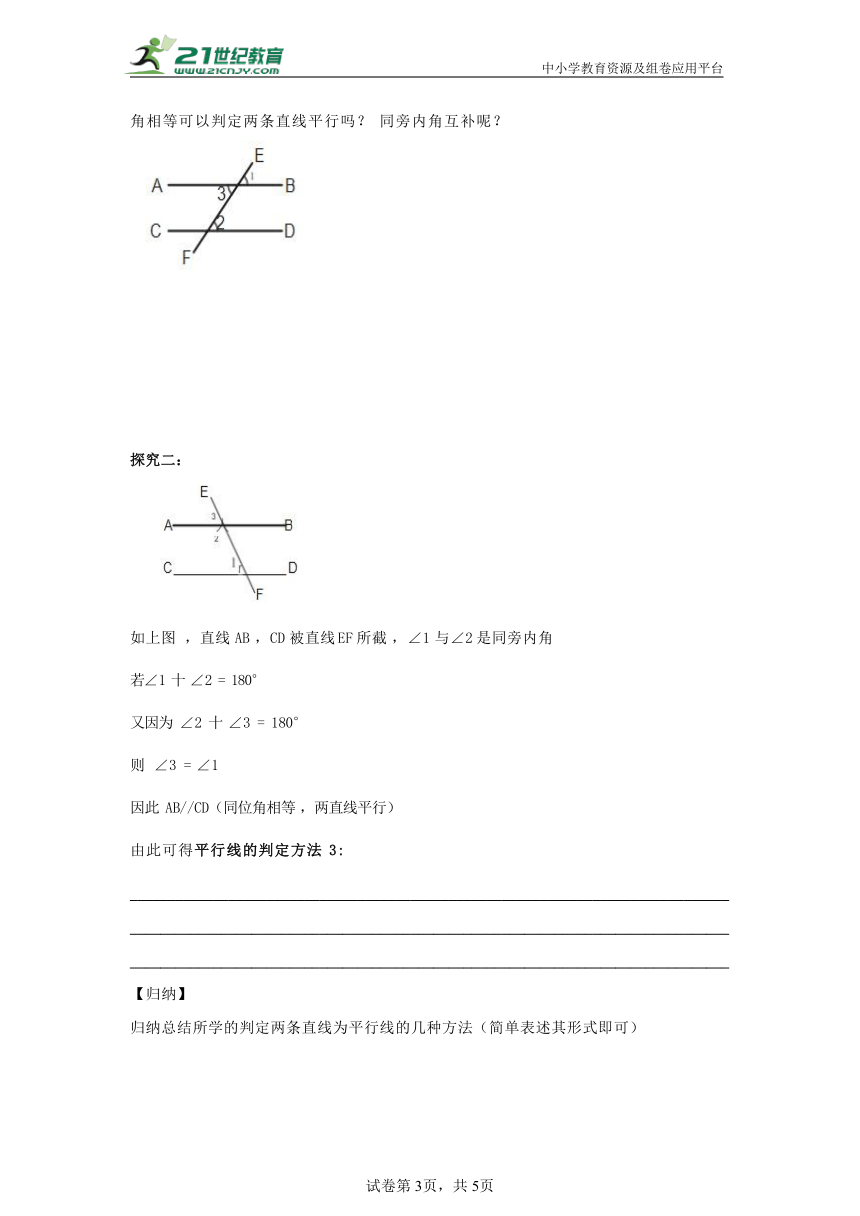
如上图 ,直线AB ,CD 被直线 EF 所截 ,∠1 与∠2 是同旁内角
若∠1 十 ∠2 = 180°
又因为 ∠2 十 ∠3 = 180°
则 ∠3 = ∠1
因此 AB//CD(同位角相等 ,两直线平行)
由此可得平行线的判定方法 3:
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
【归纳】
归纳总结所学的判定两条直线为平行线的几种方法(简单表述其形式即可)
【例题详解】
例 3 如图,AB// DC ,∠BAD = ∠BCD.那么AD// BC 吗?
例 4 如图 ,∠1 = ∠2,AD// BC ,那么AB//DC 吗
三、自主检测
一、单选题
1.如图,点E在延长线上,下列条件:①,②,③,④,不能判定的有( )
A.1个 B.2个 C.3个 D.4个
2.如图,对于下列条件:①;②;③;④,其中一定能得到的条件有( )
A.①② B.②③ C.②④ D.③④
3.如图,下列条件:①,②,③,④,⑤中能判断直线的有( )
A.5个 B.4个 C.3个 D.2个
4.将一直角三角尺与纸条按如图方式放置,下列条件:①;②;③;④.其中能说明纸条两边平行的个数有( )
A.1个 B.2个 C.3个 D.4个
二、解答题
5.光线从空气中射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.如图是光线从空气中射入水中,再从水中射入空气中的示意图.已知,.请你用所学知识来判断c与d是否平行?并说明理由.
中小学教育资源及组卷应用平台
试卷第1页,共3页
试卷第1页,共3页
知识点总结
1.平行线的判定方法 2:
两条直线被第三条直线所截, 如果内错角相等, 那么这两条直线平行 .
通常简单说成: 内错角相等, 两直线平行
2.平行线的判定方法 3:
两条直线被第三条直线所截, 如果同旁内角互补, 那么这两条直线平行
通常简单说成: 同旁内角互补, 两直线平行
答案
预习:
1.C
【分析】本题考查平行线的判定,掌握内错角相等,两直线平行是解题的关键.
【详解】解:∵,
∴,
故选C.
2.内错角相等,两直线平行
【分析】由两个三角尺的形状、大小相同可得,由内错角相等,两直线平行可得,即可得到答案.
【详解】解:由题意可得:,
(内错角相等,两直线平行),
故答案为:内错角相等,两直线平行.
【点睛】本题主要考查了平行线的判定,熟练掌握内错角相等,两直线平行,是解题的关键.
3.
【分析】本题主要考查了平行线的判定,熟知同旁内角互补,两直线平行是解题的关键.
【详解】解:∵,
∴(同旁内角互补,两直线平行),
故答案为:.
4.平行
自主:
1.A
【分析】本题考查了平行线的判定.根据平行线的判定方法直接判定.
【详解】①与是直线、被所截形成的内错角,因为,所以应是,故错误;
②,∴ (内错角相等,两直线平行),故正确;
③,∴ (内错角相等,两直线平行),故正确;
④,∴(同旁内角互补,两直线平行),故正确;
故选:A.
2.B
【分析】本题考查了平行线的判定,根据平行线的判定定理逐项判断即可.
【详解】解:,
,不能判断出,故①不符合题意;
,
,故②符合题意;
,
,故③符合题意;
,
,不能判断出,故④不符合题意;
综上所述,②③能得到,
故选:B.
3.B
【分析】本题考查平行线的判定,根据平行线的判定方法逐一进行判断即可.
【详解】解:∵,
∴(内错角相等,两直线平行);故①符合题意;
∵,
∴(同旁内角互补,两直线平行);故②符合题意;
∵,
∴(同位角相等,两直线平行);故③符合题意;
无法判断,故④不符合题意;
∵,
∴,
∴(内错角相等,两直线平行);故⑤符合题意;
综上:正确的有4个;
故选B.
4.C
【分析】本题主要考查平行线的判定,熟悉平行线的判定定理是解题的关键;根据平行线的判定定理逐个判断即可.
【详解】解:∵,
∴纸条两边平行(同位角相等,两直线平行),故①正确;
∵,
∴纸条两边平行(内错角相等,两直线平行),故②正确;
∵,
∴纸条两边平行(同旁内角互补,两直线平行),
故④正确.
∴有3个.
故选:C.
5.平行,理由见解析
【分析】本题考查平行线的判定定理,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行,想要证明,结合图形只要先证明,再利用内错角相等,两直线平行即可.
【详解】解:,理由如下:
∵,,
∴,
∵,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.4.2 平行线的判定
学习目标与重难点
学习目标:
1.学习平行线判定方法2和判定方法3,并了解学习各方法在具体题目中的实际运用;
2.掌握平行线判定方法的推理证明过程,进一步学习推理,证明的方法、格式等;
3.通过简单的推理过程的学习,培养学生进行数学推理的习惯和方法,同时培养提高学生“观察-分析-推理-论证”的能力.
学习重点:平行线判定方法2和判定方法3的推理过程及几何解题的基本格式;
学习难点:判定定理的形成过程中的逻辑推理思路及用数学语言描述、书写的格式等.
预习自测
一、单选题
1.如图,要得到,则需要条件( )
A. B.
C. D.
二、填空题
2.把两块形状、大小相同的三角尺按照如图所示的样子放置,则,理由是 .
3.如图,已知直线分别与直线,相交,,那么与的位置关系是 .
4.同旁内角互补,两直线 .
教学过程
一、创设情境、导入新课
【复习导入】
叙述平行线的判定方法1;
结合图形用数学语言叙述平行线的判定方法1;
我们学习平行线的性质定理时,有几条定理?那么两条直线平行的判定方法除了判定方法1外,是否还有其它的方法呢?
二、合作交流、新知探究
探究一:
两条直线被第三条直线所截, 由同位角相等可以判定两条直线平行,那么内错角相等可以判定两条直线平行吗? 同旁内角互补呢?
探究二:
如上图 ,直线AB ,CD 被直线 EF 所截 ,∠1 与∠2 是同旁内角
若∠1 十 ∠2 = 180°
又因为 ∠2 十 ∠3 = 180°
则 ∠3 = ∠1
因此 AB//CD(同位角相等 ,两直线平行)
由此可得平行线的判定方法 3:
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
【归纳】
归纳总结所学的判定两条直线为平行线的几种方法(简单表述其形式即可)
【例题详解】
例 3 如图,AB// DC ,∠BAD = ∠BCD.那么AD// BC 吗?
例 4 如图 ,∠1 = ∠2,AD// BC ,那么AB//DC 吗
三、自主检测
一、单选题
1.如图,点E在延长线上,下列条件:①,②,③,④,不能判定的有( )
A.1个 B.2个 C.3个 D.4个
2.如图,对于下列条件:①;②;③;④,其中一定能得到的条件有( )
A.①② B.②③ C.②④ D.③④
3.如图,下列条件:①,②,③,④,⑤中能判断直线的有( )
A.5个 B.4个 C.3个 D.2个
4.将一直角三角尺与纸条按如图方式放置,下列条件:①;②;③;④.其中能说明纸条两边平行的个数有( )
A.1个 B.2个 C.3个 D.4个
二、解答题
5.光线从空气中射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.如图是光线从空气中射入水中,再从水中射入空气中的示意图.已知,.请你用所学知识来判断c与d是否平行?并说明理由.
中小学教育资源及组卷应用平台
试卷第1页,共3页
试卷第1页,共3页
知识点总结
1.平行线的判定方法 2:
两条直线被第三条直线所截, 如果内错角相等, 那么这两条直线平行 .
通常简单说成: 内错角相等, 两直线平行
2.平行线的判定方法 3:
两条直线被第三条直线所截, 如果同旁内角互补, 那么这两条直线平行
通常简单说成: 同旁内角互补, 两直线平行
答案
预习:
1.C
【分析】本题考查平行线的判定,掌握内错角相等,两直线平行是解题的关键.
【详解】解:∵,
∴,
故选C.
2.内错角相等,两直线平行
【分析】由两个三角尺的形状、大小相同可得,由内错角相等,两直线平行可得,即可得到答案.
【详解】解:由题意可得:,
(内错角相等,两直线平行),
故答案为:内错角相等,两直线平行.
【点睛】本题主要考查了平行线的判定,熟练掌握内错角相等,两直线平行,是解题的关键.
3.
【分析】本题主要考查了平行线的判定,熟知同旁内角互补,两直线平行是解题的关键.
【详解】解:∵,
∴(同旁内角互补,两直线平行),
故答案为:.
4.平行
自主:
1.A
【分析】本题考查了平行线的判定.根据平行线的判定方法直接判定.
【详解】①与是直线、被所截形成的内错角,因为,所以应是,故错误;
②,∴ (内错角相等,两直线平行),故正确;
③,∴ (内错角相等,两直线平行),故正确;
④,∴(同旁内角互补,两直线平行),故正确;
故选:A.
2.B
【分析】本题考查了平行线的判定,根据平行线的判定定理逐项判断即可.
【详解】解:,
,不能判断出,故①不符合题意;
,
,故②符合题意;
,
,故③符合题意;
,
,不能判断出,故④不符合题意;
综上所述,②③能得到,
故选:B.
3.B
【分析】本题考查平行线的判定,根据平行线的判定方法逐一进行判断即可.
【详解】解:∵,
∴(内错角相等,两直线平行);故①符合题意;
∵,
∴(同旁内角互补,两直线平行);故②符合题意;
∵,
∴(同位角相等,两直线平行);故③符合题意;
无法判断,故④不符合题意;
∵,
∴,
∴(内错角相等,两直线平行);故⑤符合题意;
综上:正确的有4个;
故选B.
4.C
【分析】本题主要考查平行线的判定,熟悉平行线的判定定理是解题的关键;根据平行线的判定定理逐个判断即可.
【详解】解:∵,
∴纸条两边平行(同位角相等,两直线平行),故①正确;
∵,
∴纸条两边平行(内错角相等,两直线平行),故②正确;
∵,
∴纸条两边平行(同旁内角互补,两直线平行),
故④正确.
∴有3个.
故选:C.
5.平行,理由见解析
【分析】本题考查平行线的判定定理,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行,想要证明,结合图形只要先证明,再利用内错角相等,两直线平行即可.
【详解】解:,理由如下:
∵,,
∴,
∵,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
