河北省邯郸市大名县、永年县、磁县、邯郸县四县2015-2016学年高一下学期期中联考数学试题
文档属性
| 名称 | 河北省邯郸市大名县、永年县、磁县、邯郸县四县2015-2016学年高一下学期期中联考数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 193.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-22 07:03:40 | ||
图片预览


文档简介
2015—2016学年度第二学期期中联考
高一数学试卷
时间:120分钟 总分:150分
第I卷
一 、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 某校高二年级有10个班,若每个班有 ( http: / / www.21cnjy.com )50名同学,均随机编号1,2,…50,为了了解他们对体育运动的兴趣,要求每班第15号同学留下来进行问卷调查,这里运用的抽样方法是( )
A.抽签法 B.系统抽样 C.随机数表法 D.分层抽样
2.某数学兴趣小组有3名男生和2名女生,从中任选出2名同学参加数学竞赛,那么对立的两个事件是( )
A.恰有1名男生与恰有2名女生 B.至少有1名男生与全是男生
C.至少有1名男生与至少有1名女生 D.至少有1名男生与全是女生
3.下列叙述随机事件的频率与概率的关系中正确的是( )
A.频率就是概率 B.频率是客观存在的,与试验次数无关
C.随着试验次数的增加,频率一般会稳定在一个常数附近
D.概率是随机的,在试验前不能确定
4.方程表示的曲线关于成轴对称图形,则 ( )
A. D+E=0 B. D+F=0
C. E+F=0 D. D+E+F=0
5.如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,其中茎为十位数,叶为个位数,甲、乙两人得分的中位数为则下列判断正确的是( )
A.X乙﹣X甲=5,甲比乙得分稳定 B.X乙﹣X甲=5,乙比甲得分稳定
C.X乙﹣X甲=10,甲比乙得分稳定 D.X乙﹣X甲=10,乙比甲得分稳定
6.点与圆上任一点连线的中点轨迹方程是( )
A. B.
C. D.
7.如图一个边长为4的正方形及其内切圆,若随机向正方形内
丢一粒豆子,则豆子落入圆内的概率是( )
A. B. C. D.
8. 已知直线与圆相切,则三条边长分别为的三角形是 ( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不存在
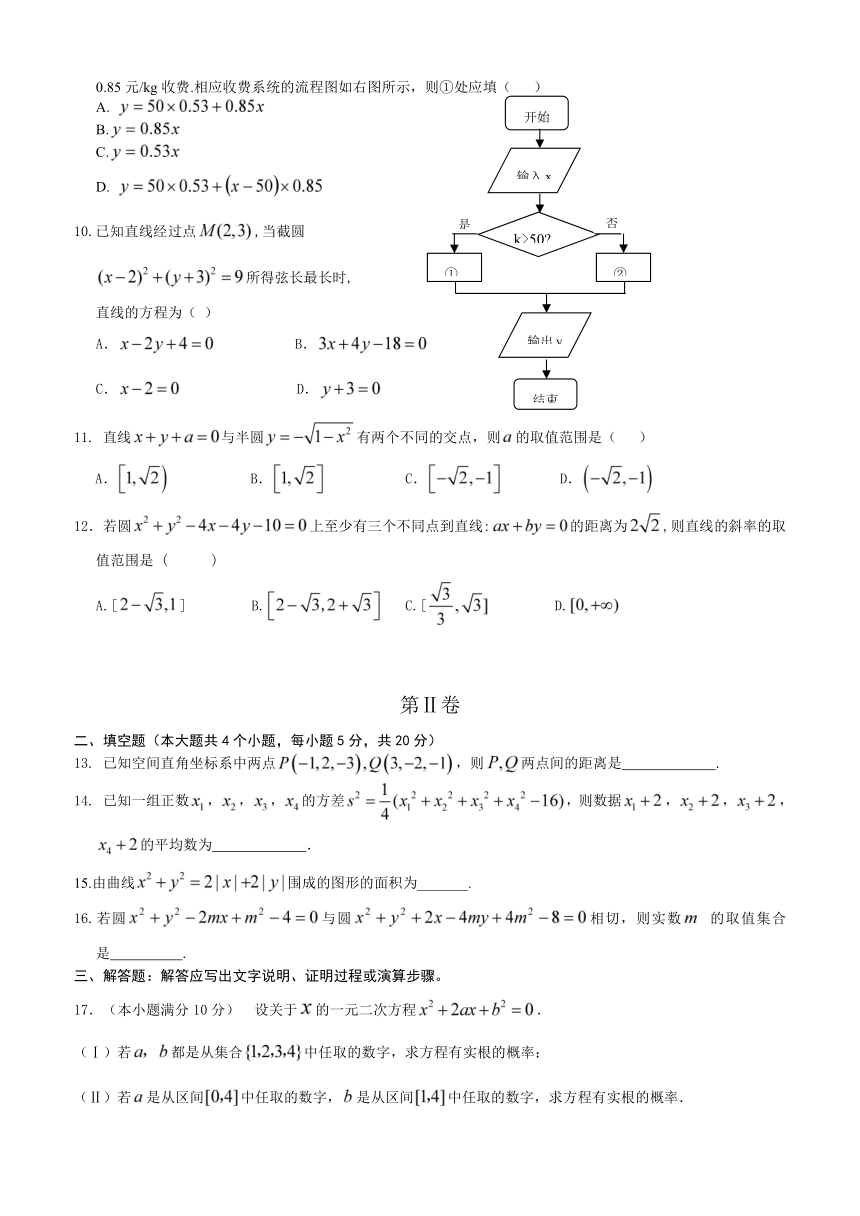
9.某铁路客运部门规定甲、乙两地之间旅客托 ( http: / / www.21cnjy.com )运行李的费用:不超过50kg按0.53元/kg收费,超过50kg的部分按0.85元/kg收费.相应收费系统的流程图如右图所示,则①处应填( )
A.
B.
C.
D.
10.已知直线经过点,当截圆
所得弦长最长时,
直线的方程为( )
A. B.
C. D.
11. 直线与半圆有两个不同的交点,则的取值范围是( )
A. B. C. D.
12.若圆上至少有三个不同点到直线:的距离为,则直线的斜率的取值范围是 ( )
A.[] B. C.[ D.
第Ⅱ卷
二、填空题(本大题共4个小题,每小题5分,共20分)
13. 已知空间直角坐标系中两点,则两点间的距离是 .
14. 已知一组正数,,,的方差,则数据,,,的平均数为 .
15.由曲线围成的图形的面积为_______.
16.若圆与圆相切,则实数 的取值集合是 .
三、解答题:解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分) 设关于的一元二次方程.
(Ⅰ)若都是从集合中任取的数字,求方程有实根的概率;
(Ⅱ)若是从区间中任取的数字,是从区间中任取的数字,求方程有实根的概率.
18.(本小题满分12分) 某学校在2015年的自主招生考试成绩中随机抽取100名学生的笔试成
绩,按成绩分组:第1组[ ( http: / / www.21cnjy.com )160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],
得到的频率分布直方图如图所示.
(1)求第3,4,5组的频率;
(2)为了能选拔出最优秀的学生,该校决 ( http: / / www.21cnjy.com )定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,则第3,4,5组每组各抽取多少名学生进入第二轮面试
(3)在第二问的前提下,学校决定在这6名学生中随机抽取2名学生接受考官甲的面试,求:第4组至少有一名学生被考官甲面试的概率
19.(本小题满分12分)
某地植被面积 (公顷)与当地气温下降的度数()之间有如下的对应数据:
(公顷) 20 40 50 60 80
() 3 4 4 4 5
⑴ 请用最小二乘法求出关于的线性回归方程;
⑵ 根据(1)中所求线性回归方程,如果植被面积为200公顷,那么下降的气温大约是多少?
参考公式:
20.(本小题满分12分)
甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
(1)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(2)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
21.(本小题满分12分) 已知圆.
(1)若圆的切线在轴和轴上的截距相等,且截距不为零,求此切线的方程;
(2)从圆外一点向该圆引一条切线,切点为,为坐标原点,且有,求使得取得最小值的点的坐标.
.22.(本小题满分12分)
已知圆:,直线被圆C所截得的弦的中点为.
(1)求直线的方程.
(2)若直线:与圆相交,求的取值范围.
(3)是否存在常数,使得直线被圆所截得的弦的中点落在直线上?若存在,求出的值;若不存在,说明理由.
2015—2016学年第二学期期中联考
高一数学试题答案
一 、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.B 2.D 3.C 4.A 5.D 6.A 7.C 8.B 9.D 10.C 11.A 12.B
二、填空题(本大题共4个小题,每小题5分,共20分)
13. 6 14. 4 15. 16.
三、解答题:解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
解:(I)设事件A为“方程有实根”,
记为取到的一组数,则所有的情况有:
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4).
一共16种且每种情况被取到的可能性相同.
∵关于的一元二次方程有实根,
∴
∴事件A包含的基本事件有:
(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),(4,1),(4,2),
(4,3),(4,4)共10种.
∴
∴方程有实根的概率是.
(Ⅱ)设事件B=“方程有实根”,记为取到的一组数.
∵是从区间[0,4]中任取的数字,是从区间[1,4]中任取的数字,
∴点所在区域是长为4,宽为3的矩形区域.
又∵满足的点的区域是如图所示的阴影部分.
∴P(B)==.
∴方程有实根的概率是.
( http: / / www.21cnjy.com )
18. (本小题满分12分)
解:(1)由题设可知,第3组的频率为0.06×5=0.3,第4组的频率为0.04×5=0.2, 第5组的频率为0.02×5=0.1.
(2) 第3组的人数为0.3×100=30,第4组的人数为0.2×100=20,第5组的人数为0.1×100=10.
因为3,4,5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组抽取的人数分别为:第3组:,第4组,第5组:
所以第3,4,5组分别抽取3人、2人、1人.
(3)设第3组的三位同学为A1,A2,A3,第4组的两位同学为B1,B2,第5组的一位同学为C1,则从六位同学中抽两位同学有:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1)共15种可能.
其中第4组的2位同学B1,B2至少有一位同学入选的有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2), (B1,C1),(B2,C1)共9种可能,
所以第4组至少有一名学生被甲考官面试的概率为
19. (本小题满分12分)
解:⑴ ,
.
,
.
所以 ,
.
故关于的线性回归方程.
⑵ 由⑴得:当时,.
所以植被面积为200公顷时,下降的气温大约是.
20.(本小题满分12分)
解:(1)从甲校和乙校报名的教师中各任选1名,所有可能的结果为(甲男1,乙男)、(甲男2,乙男)、(甲男1,乙女1)、(甲男1,乙女2)、(甲男2,乙女1)、(甲男2,乙女2)、(甲女,乙女1)、(甲女,乙女2)、(甲女,乙男),共9种;选出的2名教师性别相同的结果有(甲男1,乙男)、(甲男2,乙男)、(甲女,乙女1)、(甲女,乙女2)共4种,所以选出的2名教师性别相同的概率为。
(2)从报名的6名教师中任选2名所有可能的结果为(甲男1,乙男)、(甲男2,乙男)、(甲男1,乙女1)、(甲男1,乙女2)、(甲男2,乙女1)、(甲男2,乙女2)、(甲女,乙女1)、(甲女,乙女2)、(甲女,乙男)、(甲男1,甲男2)、(甲男1,甲女)、(甲男2,甲女)、(乙男,乙女1)、(乙男,乙女2)、(乙女1,乙女2)共15种,选出的2名教师来自同一学校的所有可能结果为(甲男1,甲男2)、(甲男1,甲女)、(甲男2,甲女)、(乙男,乙女1)、(乙男,乙女2)、(乙女1,乙女2),共6种结果,选出的2名教师来自同一学校的概率为
21.(本小题满分12分)
解:(1)∵切线在两坐标轴上的截距相等且截距不为零,
∴设切线方程为,
又∵圆,∴圆心到切线的距离等于圆的半径,
∴,或,则所求切线的方程为或.
(2)∵切线与半径垂直,∴,
∴,
∴,∴动点的轨迹是直线.
的最小值就是的最小值,而的最小值为到直线的距离.此时点坐标为.
22.(本小题满分12分)
解:(1)圆的方程化为标准方程:,
则其圆心,半径.
若设直线的斜率为,则.
∴直线的方程为,即.
(2)∵圆的半径,
∴要使直线与圆相交,则须有.
∴.
于是的取值范围是.
(3)设直线被圆截得的弦的中点为,
则直线与垂直,于是有=1,整理可得.
又∵点在直线上,∴.
( http: / / www.21cnjy.com )
代入直线的方程,得,
于是,
故存在满足条件的常数.
输出y
是
开始
输入x
k>50
结束
否
①
②
高一数学试卷
时间:120分钟 总分:150分
第I卷
一 、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 某校高二年级有10个班,若每个班有 ( http: / / www.21cnjy.com )50名同学,均随机编号1,2,…50,为了了解他们对体育运动的兴趣,要求每班第15号同学留下来进行问卷调查,这里运用的抽样方法是( )
A.抽签法 B.系统抽样 C.随机数表法 D.分层抽样
2.某数学兴趣小组有3名男生和2名女生,从中任选出2名同学参加数学竞赛,那么对立的两个事件是( )
A.恰有1名男生与恰有2名女生 B.至少有1名男生与全是男生
C.至少有1名男生与至少有1名女生 D.至少有1名男生与全是女生
3.下列叙述随机事件的频率与概率的关系中正确的是( )
A.频率就是概率 B.频率是客观存在的,与试验次数无关
C.随着试验次数的增加,频率一般会稳定在一个常数附近
D.概率是随机的,在试验前不能确定
4.方程表示的曲线关于成轴对称图形,则 ( )
A. D+E=0 B. D+F=0
C. E+F=0 D. D+E+F=0
5.如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,其中茎为十位数,叶为个位数,甲、乙两人得分的中位数为则下列判断正确的是( )
A.X乙﹣X甲=5,甲比乙得分稳定 B.X乙﹣X甲=5,乙比甲得分稳定
C.X乙﹣X甲=10,甲比乙得分稳定 D.X乙﹣X甲=10,乙比甲得分稳定
6.点与圆上任一点连线的中点轨迹方程是( )
A. B.
C. D.
7.如图一个边长为4的正方形及其内切圆,若随机向正方形内
丢一粒豆子,则豆子落入圆内的概率是( )
A. B. C. D.
8. 已知直线与圆相切,则三条边长分别为的三角形是 ( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不存在
9.某铁路客运部门规定甲、乙两地之间旅客托 ( http: / / www.21cnjy.com )运行李的费用:不超过50kg按0.53元/kg收费,超过50kg的部分按0.85元/kg收费.相应收费系统的流程图如右图所示,则①处应填( )
A.
B.
C.
D.
10.已知直线经过点,当截圆
所得弦长最长时,
直线的方程为( )
A. B.
C. D.
11. 直线与半圆有两个不同的交点,则的取值范围是( )
A. B. C. D.
12.若圆上至少有三个不同点到直线:的距离为,则直线的斜率的取值范围是 ( )
A.[] B. C.[ D.
第Ⅱ卷
二、填空题(本大题共4个小题,每小题5分,共20分)
13. 已知空间直角坐标系中两点,则两点间的距离是 .
14. 已知一组正数,,,的方差,则数据,,,的平均数为 .
15.由曲线围成的图形的面积为_______.
16.若圆与圆相切,则实数 的取值集合是 .
三、解答题:解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分) 设关于的一元二次方程.
(Ⅰ)若都是从集合中任取的数字,求方程有实根的概率;
(Ⅱ)若是从区间中任取的数字,是从区间中任取的数字,求方程有实根的概率.
18.(本小题满分12分) 某学校在2015年的自主招生考试成绩中随机抽取100名学生的笔试成
绩,按成绩分组:第1组[ ( http: / / www.21cnjy.com )160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],
得到的频率分布直方图如图所示.
(1)求第3,4,5组的频率;
(2)为了能选拔出最优秀的学生,该校决 ( http: / / www.21cnjy.com )定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,则第3,4,5组每组各抽取多少名学生进入第二轮面试
(3)在第二问的前提下,学校决定在这6名学生中随机抽取2名学生接受考官甲的面试,求:第4组至少有一名学生被考官甲面试的概率
19.(本小题满分12分)
某地植被面积 (公顷)与当地气温下降的度数()之间有如下的对应数据:
(公顷) 20 40 50 60 80
() 3 4 4 4 5
⑴ 请用最小二乘法求出关于的线性回归方程;
⑵ 根据(1)中所求线性回归方程,如果植被面积为200公顷,那么下降的气温大约是多少?
参考公式:
20.(本小题满分12分)
甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
(1)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(2)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
21.(本小题满分12分) 已知圆.
(1)若圆的切线在轴和轴上的截距相等,且截距不为零,求此切线的方程;
(2)从圆外一点向该圆引一条切线,切点为,为坐标原点,且有,求使得取得最小值的点的坐标.
.22.(本小题满分12分)
已知圆:,直线被圆C所截得的弦的中点为.
(1)求直线的方程.
(2)若直线:与圆相交,求的取值范围.
(3)是否存在常数,使得直线被圆所截得的弦的中点落在直线上?若存在,求出的值;若不存在,说明理由.
2015—2016学年第二学期期中联考
高一数学试题答案
一 、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.B 2.D 3.C 4.A 5.D 6.A 7.C 8.B 9.D 10.C 11.A 12.B
二、填空题(本大题共4个小题,每小题5分,共20分)
13. 6 14. 4 15. 16.
三、解答题:解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
解:(I)设事件A为“方程有实根”,
记为取到的一组数,则所有的情况有:
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4).
一共16种且每种情况被取到的可能性相同.
∵关于的一元二次方程有实根,
∴
∴事件A包含的基本事件有:
(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),(4,1),(4,2),
(4,3),(4,4)共10种.
∴
∴方程有实根的概率是.
(Ⅱ)设事件B=“方程有实根”,记为取到的一组数.
∵是从区间[0,4]中任取的数字,是从区间[1,4]中任取的数字,
∴点所在区域是长为4,宽为3的矩形区域.
又∵满足的点的区域是如图所示的阴影部分.
∴P(B)==.
∴方程有实根的概率是.
( http: / / www.21cnjy.com )
18. (本小题满分12分)
解:(1)由题设可知,第3组的频率为0.06×5=0.3,第4组的频率为0.04×5=0.2, 第5组的频率为0.02×5=0.1.
(2) 第3组的人数为0.3×100=30,第4组的人数为0.2×100=20,第5组的人数为0.1×100=10.
因为3,4,5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组抽取的人数分别为:第3组:,第4组,第5组:
所以第3,4,5组分别抽取3人、2人、1人.
(3)设第3组的三位同学为A1,A2,A3,第4组的两位同学为B1,B2,第5组的一位同学为C1,则从六位同学中抽两位同学有:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1)共15种可能.
其中第4组的2位同学B1,B2至少有一位同学入选的有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2), (B1,C1),(B2,C1)共9种可能,
所以第4组至少有一名学生被甲考官面试的概率为
19. (本小题满分12分)
解:⑴ ,
.
,
.
所以 ,
.
故关于的线性回归方程.
⑵ 由⑴得:当时,.
所以植被面积为200公顷时,下降的气温大约是.
20.(本小题满分12分)
解:(1)从甲校和乙校报名的教师中各任选1名,所有可能的结果为(甲男1,乙男)、(甲男2,乙男)、(甲男1,乙女1)、(甲男1,乙女2)、(甲男2,乙女1)、(甲男2,乙女2)、(甲女,乙女1)、(甲女,乙女2)、(甲女,乙男),共9种;选出的2名教师性别相同的结果有(甲男1,乙男)、(甲男2,乙男)、(甲女,乙女1)、(甲女,乙女2)共4种,所以选出的2名教师性别相同的概率为。
(2)从报名的6名教师中任选2名所有可能的结果为(甲男1,乙男)、(甲男2,乙男)、(甲男1,乙女1)、(甲男1,乙女2)、(甲男2,乙女1)、(甲男2,乙女2)、(甲女,乙女1)、(甲女,乙女2)、(甲女,乙男)、(甲男1,甲男2)、(甲男1,甲女)、(甲男2,甲女)、(乙男,乙女1)、(乙男,乙女2)、(乙女1,乙女2)共15种,选出的2名教师来自同一学校的所有可能结果为(甲男1,甲男2)、(甲男1,甲女)、(甲男2,甲女)、(乙男,乙女1)、(乙男,乙女2)、(乙女1,乙女2),共6种结果,选出的2名教师来自同一学校的概率为
21.(本小题满分12分)
解:(1)∵切线在两坐标轴上的截距相等且截距不为零,
∴设切线方程为,
又∵圆,∴圆心到切线的距离等于圆的半径,
∴,或,则所求切线的方程为或.
(2)∵切线与半径垂直,∴,
∴,
∴,∴动点的轨迹是直线.
的最小值就是的最小值,而的最小值为到直线的距离.此时点坐标为.
22.(本小题满分12分)
解:(1)圆的方程化为标准方程:,
则其圆心,半径.
若设直线的斜率为,则.
∴直线的方程为,即.
(2)∵圆的半径,
∴要使直线与圆相交,则须有.
∴.
于是的取值范围是.
(3)设直线被圆截得的弦的中点为,
则直线与垂直,于是有=1,整理可得.
又∵点在直线上,∴.
( http: / / www.21cnjy.com )
代入直线的方程,得,
于是,
故存在满足条件的常数.
输出y
是
开始
输入x
k>50
结束
否
①
②
同课章节目录
