27.3 位似 同步练习 2024--2025学年初中数学人教版九年级下册
文档属性
| 名称 | 27.3 位似 同步练习 2024--2025学年初中数学人教版九年级下册 | 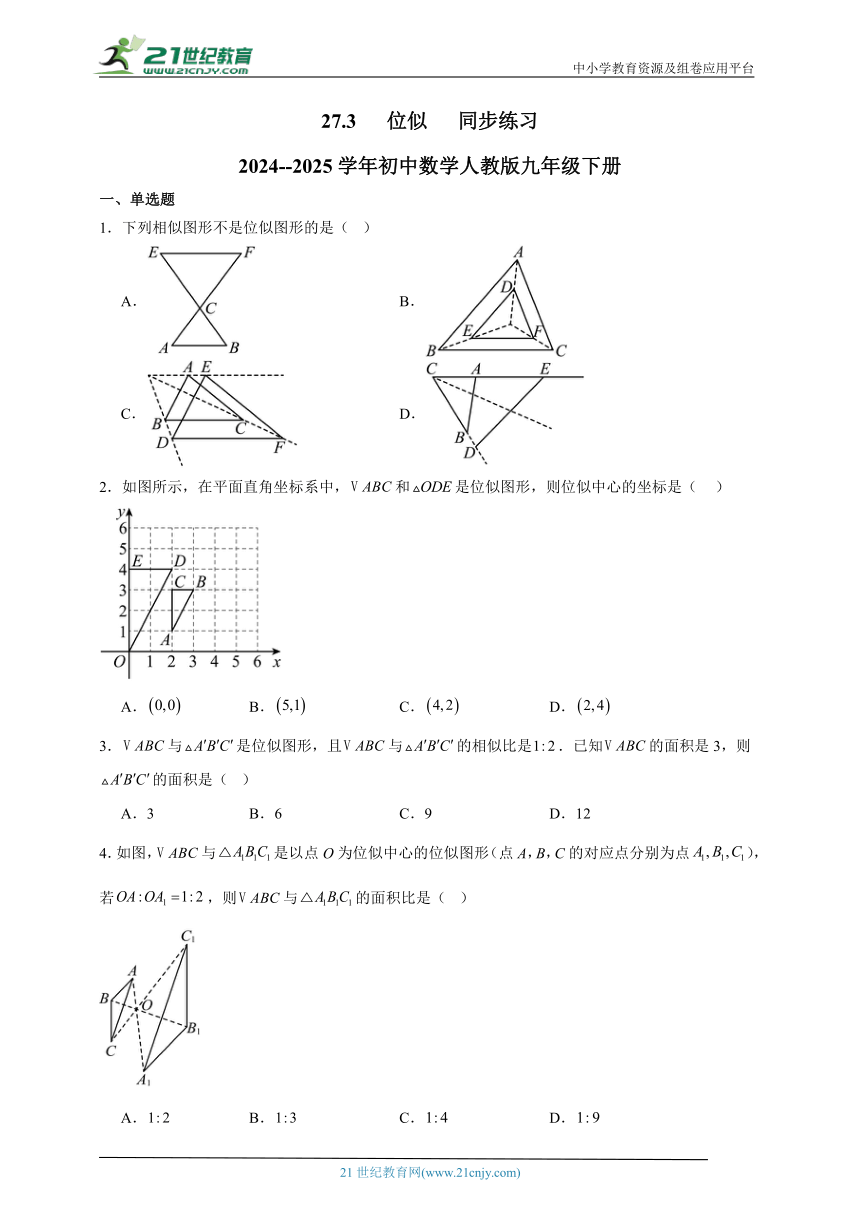 | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-18 09:59:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
27.3 位似 同步练习
2024--2025学年初中数学人教版九年级下册
一、单选题
1.下列相似图形不是位似图形的是( )
A. B.
C. D.
2.如图所示,在平面直角坐标系中,和是位似图形,则位似中心的坐标是( )
A. B. C. D.
3.与是位似图形,且与的相似比是.已知的面积是3,则的面积是( )
A.3 B.6 C.9 D.12
4.如图,与是以点O为位似中心的位似图形(点A,B,C的对应点分别为点),若,则与的面积比是( )
A. B. C. D.
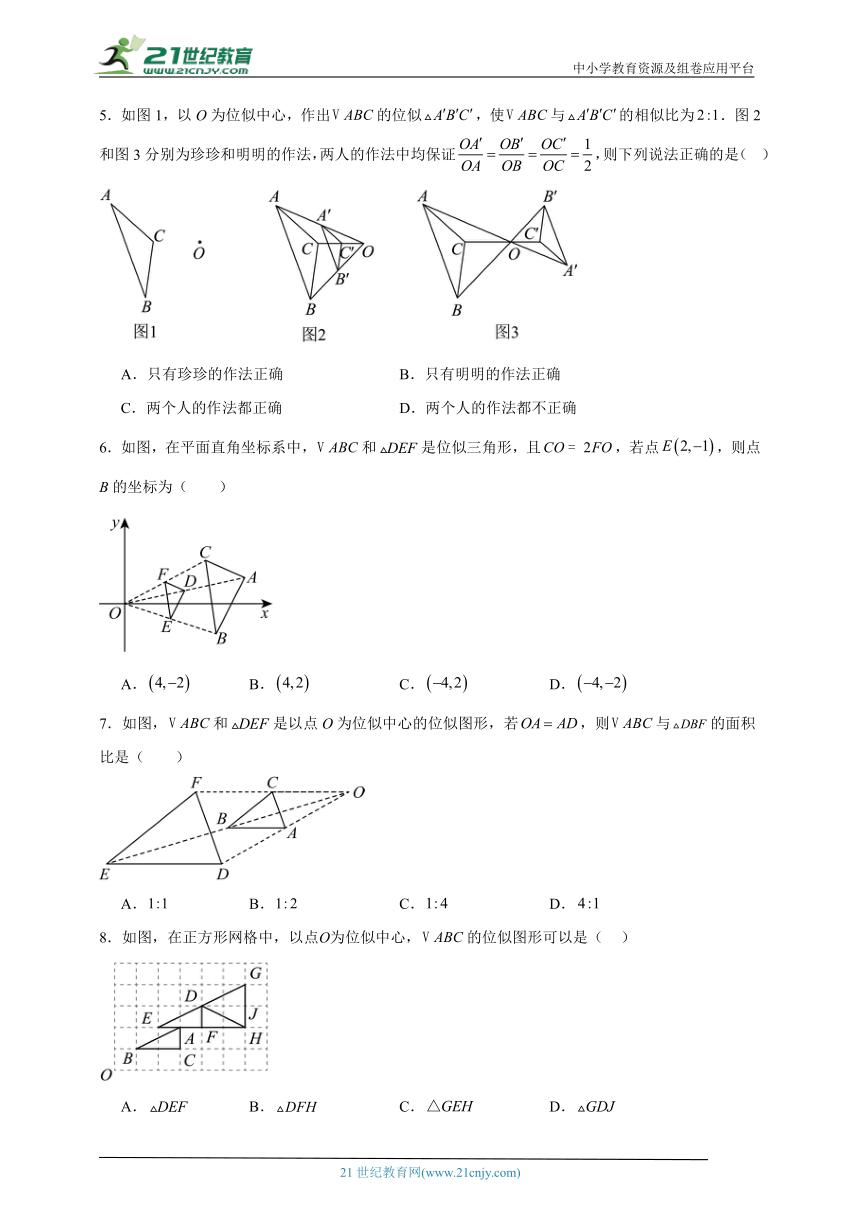
5.如图1,以O为位似中心,作出的位似,使与的相似比为.图2和图3分别为珍珍和明明的作法,两人的作法中均保证,则下列说法正确的是( )
A.只有珍珍的作法正确 B.只有明明的作法正确
C.两个人的作法都正确 D.两个人的作法都不正确
6.如图,在平面直角坐标系中,和是位似三角形,且,若点,则点B的坐标为( )
A. B. C. D.
7.如图,和是以点O为位似中心的位似图形,若,则与的面积比是( )
A. B. C. D.
8.如图,在正方形网格中,以点О为位似中心,的位似图形可以是( )
A. B. C. D.
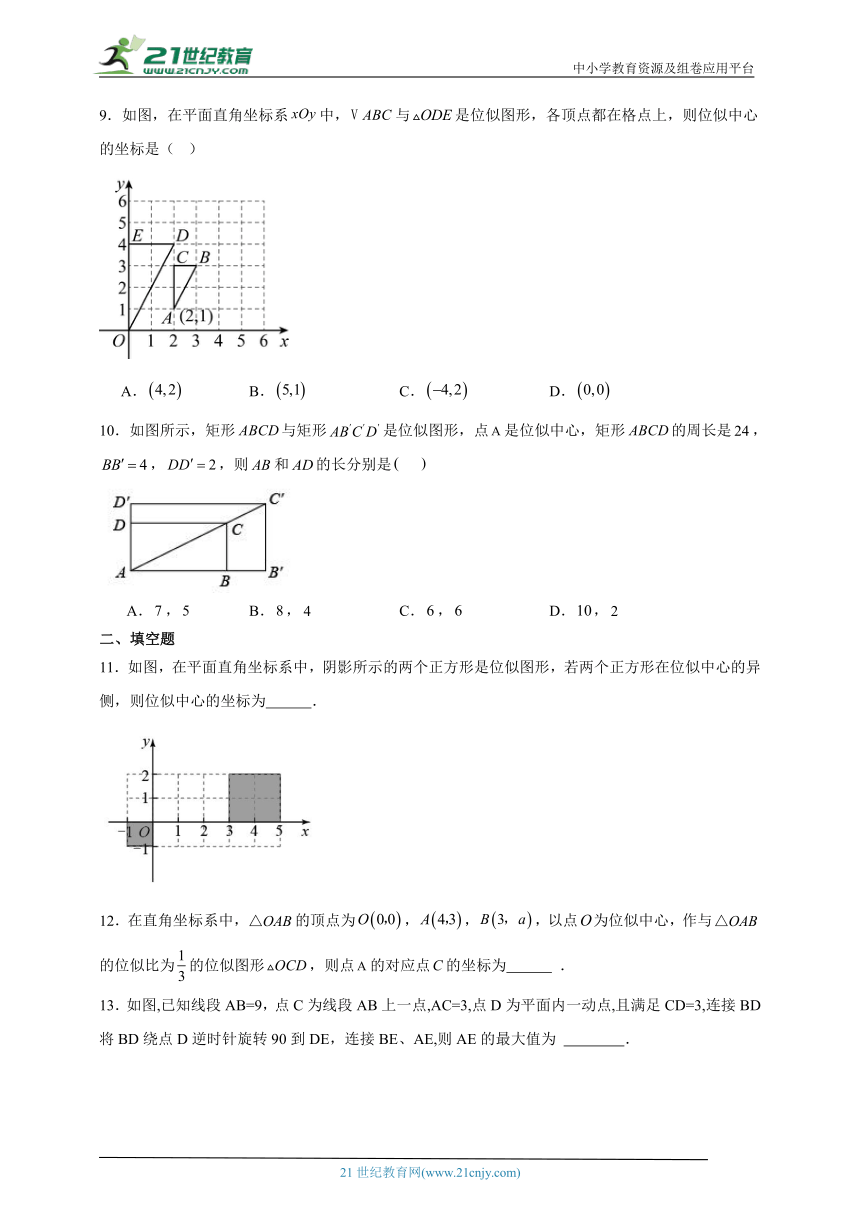
9.如图,在平面直角坐标系中,与是位似图形,各顶点都在格点上,则位似中心的坐标是( )
A. B. C. D.
10.如图所示,矩形与矩形是位似图形,点是位似中心,矩形的周长是,,,则和的长分别是
A., B., C., D.,
二、填空题
11.如图,在平面直角坐标系中,阴影所示的两个正方形是位似图形,若两个正方形在位似中心的异侧,则位似中心的坐标为 .
12.在直角坐标系中,的顶点为,,,以点为位似中心,作与的位似比为的位似图形,则点的对应点的坐标为 .
13.如图,已知线段AB=9,点C为线段AB上一点,AC=3,点D为平面内一动点,且满足CD=3,连接BD将BD绕点D逆时针旋转90到DE,连接BE、AE,则AE的最大值为 .
14.如图,平面直角坐标系中有正方形和正方形,若点和点的坐标分别为,,则两个正方形的位似中心的坐标是 .
三、解答题
15.如图,在由边长为1的小正方形组成的网格图中,已知点O及的顶点均为网格线的交点.
(1)将绕着点B顺时针旋转90°,得到,请在网格中画出;
(2)以点O为位似中心,将放大为原来的三倍,得到,请在网格中画出.
16.如图是一个的正方形网格和平面直角坐标系,网格的每个小正方形边长为l,顶点都为格点的三角形我们称作格点三角形.如图是格点三角形.
(1)将绕点顺时针旋转90°,得到对应图形;
(2)在网格中,以为位似中心,同侧将按2:1放大,对应得到,画出,直接写出点坐标.
17.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点(顶点是网格线的交点).
(1)以点为位似中心,在网格中画出,使与的位似比为;
(2)将向右平移7格,再向下平移2格,得到,画出;
(3)借助网格,在上选一点,使得平分的面积(保留确定关键点的画法),画出线段.
18.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣2,4),B(4,4),C(6,0).
(1)请以原点O为位似中心,画出△A'B'C',使它与△ABC的相似比为1:2,变换后点A、B的对应点分别为点A'、B',点B'在第一象限,并写出点A'的坐标 ;
(2)若P(a,b)为线段BC上的任一点,则变换后点P的对应点P'的坐标为 .
19.如图,在的网格中,每个小正方形的边长均为1,点O和的顶点均为格点,请你仅用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:
(1)如图1,在的内部作,使和位似,且位似中心为点O,位似比为;
(2)连接图1中的,则线段的长度是______.
(3)如图2,在AC上取点P,使得,连接AO,作出点P关于AO的对称点Q.
参考答案
1.D
解:根据位似图形的定义,选项A,B,C是位似图形,位似中心是交点,不符合题意;
选项D中,对应边、不平行,故不是位似图形,符合题意.
2.C
解:如图,分别连接、、,其所在直线交于点
则点G为所求的位似中心,
3.D
解:∵与是位似图形,与位似比是,
∴,且与相似比是,
∴与面积比是,
∵,
∴,
4.C
解:∵与是以点O为位似中心的位似图形,,
∴,
∵
,
∴
和的相似比为,
和的面积之比为,
5.C
解:确定位似中心;分别连接并延长位似中心和顶点;根据相似比,确定对应点的位似图形的点;顺次连接各点,得到位视图形;而珍珍和明明画的位似图形,对应边满足比值等于位似比,则珍珍和明明都正确.
6.A
解:和是位似三角形,且,则位似比为,点,
∴点B的坐标为,
7.C
解:,
,
和是以点为位似中心的位似图形,
,,
,,
,
,
与的面积比为:,
8.C
解:连接,,,并延长如图所示,
,
∴的位似图形是,
9.A
如图所示:位似中心的坐标是.
故选:A.
10.B
解:∵矩形ABCD的周长是24,
∴,
∴,
∵,,
∴,
∵矩形ABCD与矩形是位似图形,
∴,
∴,,
∴,即,
解得,,
则,
11.
解:如图,点为位似中心,.
故答案为:.
12.或
解:以点为位似中心,作与的位似比为的位似图形,
而,
或,
即或,
故答案为:或.
13.
解:以BC为直角边在BC上方作等腰直角三角形BOC,如图,连接AO、OE.
则,
∵∠EBD=∠OBC,
∴∠EBO=∠DBC,
∴△EBO∽△DBC.
∴.
∵D点运动轨迹是以C为圆心,CD=3为半径的圆,
∴E点运动的轨迹是以O为圆心,OE=为半径的圆.
∵AE≤AO+OE,AO=,OE=.
∴AE最大值为:.
故答案为.
14. 或
解:∵平面直角坐标系中有正方形和正方形,点和点的坐标分别为,,
∴,,,
(1)当点和是对应顶点,和是对应顶点时,位似中心就是与的交点,
如图所示:连接,交轴于点,
点即为两个正方形的位似中心,
设所在直线解析式为:,把,代入得:
故,
解得:,
故;
当时,即,解得,即点坐标为,,
两个正方形的位似中心的坐标是:,.
(2)当点和是对应顶点,和是对应顶点时,位似中心就是与的交点,
如图所示:连接,,,并延长交于点,
设所在直线解析式为:,把,代入得:
故,
解得:,
故;
设所在直线解析式为:,把,代入得:
,
故,
联立直线BH、AG得方程组:
,
解得:,
故,
综上所述:两个正方形的位似中心的坐标是:,或.
故答案为:,或.
15.(1)如图见解析;(2)如图见解析.
(1)如图所示,即为所求,
(2)如图所示,即为所求
16.(1)作图见解析
(2)作图见解析,点C2坐标为
(1)解:如图所示
(2)解:如图所示
由图可知点C2的坐标为
17.(1)见解析
(2)见解析
(3)见解析
(1)解:如图所示:即为所求;
(2)如图所示:即为所求;
(3)如图所示:线段即为所求.
18.(1)图见解析,(-1,2);(2)(,).
解:(1)如图所示:△A'B'C'即为所求,点A'的坐标(-1,2);
(2)若P(a,b)为线段BC上的任一点,则变换后点P的对应点P'的坐标为:(,).
故答案为:(,).
19.(1)将详解
(2)
(3)见详解
(1)如图1所示,即为所求,
(2)由图可知;
(3)如图2所示,点P,点Q即为所求,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
27.3 位似 同步练习
2024--2025学年初中数学人教版九年级下册
一、单选题
1.下列相似图形不是位似图形的是( )
A. B.
C. D.
2.如图所示,在平面直角坐标系中,和是位似图形,则位似中心的坐标是( )
A. B. C. D.
3.与是位似图形,且与的相似比是.已知的面积是3,则的面积是( )
A.3 B.6 C.9 D.12
4.如图,与是以点O为位似中心的位似图形(点A,B,C的对应点分别为点),若,则与的面积比是( )
A. B. C. D.
5.如图1,以O为位似中心,作出的位似,使与的相似比为.图2和图3分别为珍珍和明明的作法,两人的作法中均保证,则下列说法正确的是( )
A.只有珍珍的作法正确 B.只有明明的作法正确
C.两个人的作法都正确 D.两个人的作法都不正确
6.如图,在平面直角坐标系中,和是位似三角形,且,若点,则点B的坐标为( )
A. B. C. D.
7.如图,和是以点O为位似中心的位似图形,若,则与的面积比是( )
A. B. C. D.
8.如图,在正方形网格中,以点О为位似中心,的位似图形可以是( )
A. B. C. D.
9.如图,在平面直角坐标系中,与是位似图形,各顶点都在格点上,则位似中心的坐标是( )
A. B. C. D.
10.如图所示,矩形与矩形是位似图形,点是位似中心,矩形的周长是,,,则和的长分别是
A., B., C., D.,
二、填空题
11.如图,在平面直角坐标系中,阴影所示的两个正方形是位似图形,若两个正方形在位似中心的异侧,则位似中心的坐标为 .
12.在直角坐标系中,的顶点为,,,以点为位似中心,作与的位似比为的位似图形,则点的对应点的坐标为 .
13.如图,已知线段AB=9,点C为线段AB上一点,AC=3,点D为平面内一动点,且满足CD=3,连接BD将BD绕点D逆时针旋转90到DE,连接BE、AE,则AE的最大值为 .
14.如图,平面直角坐标系中有正方形和正方形,若点和点的坐标分别为,,则两个正方形的位似中心的坐标是 .
三、解答题
15.如图,在由边长为1的小正方形组成的网格图中,已知点O及的顶点均为网格线的交点.
(1)将绕着点B顺时针旋转90°,得到,请在网格中画出;
(2)以点O为位似中心,将放大为原来的三倍,得到,请在网格中画出.
16.如图是一个的正方形网格和平面直角坐标系,网格的每个小正方形边长为l,顶点都为格点的三角形我们称作格点三角形.如图是格点三角形.
(1)将绕点顺时针旋转90°,得到对应图形;
(2)在网格中,以为位似中心,同侧将按2:1放大,对应得到,画出,直接写出点坐标.
17.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点(顶点是网格线的交点).
(1)以点为位似中心,在网格中画出,使与的位似比为;
(2)将向右平移7格,再向下平移2格,得到,画出;
(3)借助网格,在上选一点,使得平分的面积(保留确定关键点的画法),画出线段.
18.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣2,4),B(4,4),C(6,0).
(1)请以原点O为位似中心,画出△A'B'C',使它与△ABC的相似比为1:2,变换后点A、B的对应点分别为点A'、B',点B'在第一象限,并写出点A'的坐标 ;
(2)若P(a,b)为线段BC上的任一点,则变换后点P的对应点P'的坐标为 .
19.如图,在的网格中,每个小正方形的边长均为1,点O和的顶点均为格点,请你仅用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:
(1)如图1,在的内部作,使和位似,且位似中心为点O,位似比为;
(2)连接图1中的,则线段的长度是______.
(3)如图2,在AC上取点P,使得,连接AO,作出点P关于AO的对称点Q.
参考答案
1.D
解:根据位似图形的定义,选项A,B,C是位似图形,位似中心是交点,不符合题意;
选项D中,对应边、不平行,故不是位似图形,符合题意.
2.C
解:如图,分别连接、、,其所在直线交于点
则点G为所求的位似中心,
3.D
解:∵与是位似图形,与位似比是,
∴,且与相似比是,
∴与面积比是,
∵,
∴,
4.C
解:∵与是以点O为位似中心的位似图形,,
∴,
∵
,
∴
和的相似比为,
和的面积之比为,
5.C
解:确定位似中心;分别连接并延长位似中心和顶点;根据相似比,确定对应点的位似图形的点;顺次连接各点,得到位视图形;而珍珍和明明画的位似图形,对应边满足比值等于位似比,则珍珍和明明都正确.
6.A
解:和是位似三角形,且,则位似比为,点,
∴点B的坐标为,
7.C
解:,
,
和是以点为位似中心的位似图形,
,,
,,
,
,
与的面积比为:,
8.C
解:连接,,,并延长如图所示,
,
∴的位似图形是,
9.A
如图所示:位似中心的坐标是.
故选:A.
10.B
解:∵矩形ABCD的周长是24,
∴,
∴,
∵,,
∴,
∵矩形ABCD与矩形是位似图形,
∴,
∴,,
∴,即,
解得,,
则,
11.
解:如图,点为位似中心,.
故答案为:.
12.或
解:以点为位似中心,作与的位似比为的位似图形,
而,
或,
即或,
故答案为:或.
13.
解:以BC为直角边在BC上方作等腰直角三角形BOC,如图,连接AO、OE.
则,
∵∠EBD=∠OBC,
∴∠EBO=∠DBC,
∴△EBO∽△DBC.
∴.
∵D点运动轨迹是以C为圆心,CD=3为半径的圆,
∴E点运动的轨迹是以O为圆心,OE=为半径的圆.
∵AE≤AO+OE,AO=,OE=.
∴AE最大值为:.
故答案为.
14. 或
解:∵平面直角坐标系中有正方形和正方形,点和点的坐标分别为,,
∴,,,
(1)当点和是对应顶点,和是对应顶点时,位似中心就是与的交点,
如图所示:连接,交轴于点,
点即为两个正方形的位似中心,
设所在直线解析式为:,把,代入得:
故,
解得:,
故;
当时,即,解得,即点坐标为,,
两个正方形的位似中心的坐标是:,.
(2)当点和是对应顶点,和是对应顶点时,位似中心就是与的交点,
如图所示:连接,,,并延长交于点,
设所在直线解析式为:,把,代入得:
故,
解得:,
故;
设所在直线解析式为:,把,代入得:
,
故,
联立直线BH、AG得方程组:
,
解得:,
故,
综上所述:两个正方形的位似中心的坐标是:,或.
故答案为:,或.
15.(1)如图见解析;(2)如图见解析.
(1)如图所示,即为所求,
(2)如图所示,即为所求
16.(1)作图见解析
(2)作图见解析,点C2坐标为
(1)解:如图所示
(2)解:如图所示
由图可知点C2的坐标为
17.(1)见解析
(2)见解析
(3)见解析
(1)解:如图所示:即为所求;
(2)如图所示:即为所求;
(3)如图所示:线段即为所求.
18.(1)图见解析,(-1,2);(2)(,).
解:(1)如图所示:△A'B'C'即为所求,点A'的坐标(-1,2);
(2)若P(a,b)为线段BC上的任一点,则变换后点P的对应点P'的坐标为:(,).
故答案为:(,).
19.(1)将详解
(2)
(3)见详解
(1)如图1所示,即为所求,
(2)由图可知;
(3)如图2所示,点P,点Q即为所求,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
