10.1相交线(含答案)
图片预览
文档简介
中小学教育资源及组卷应用平台
10.1相交线
一、填空题
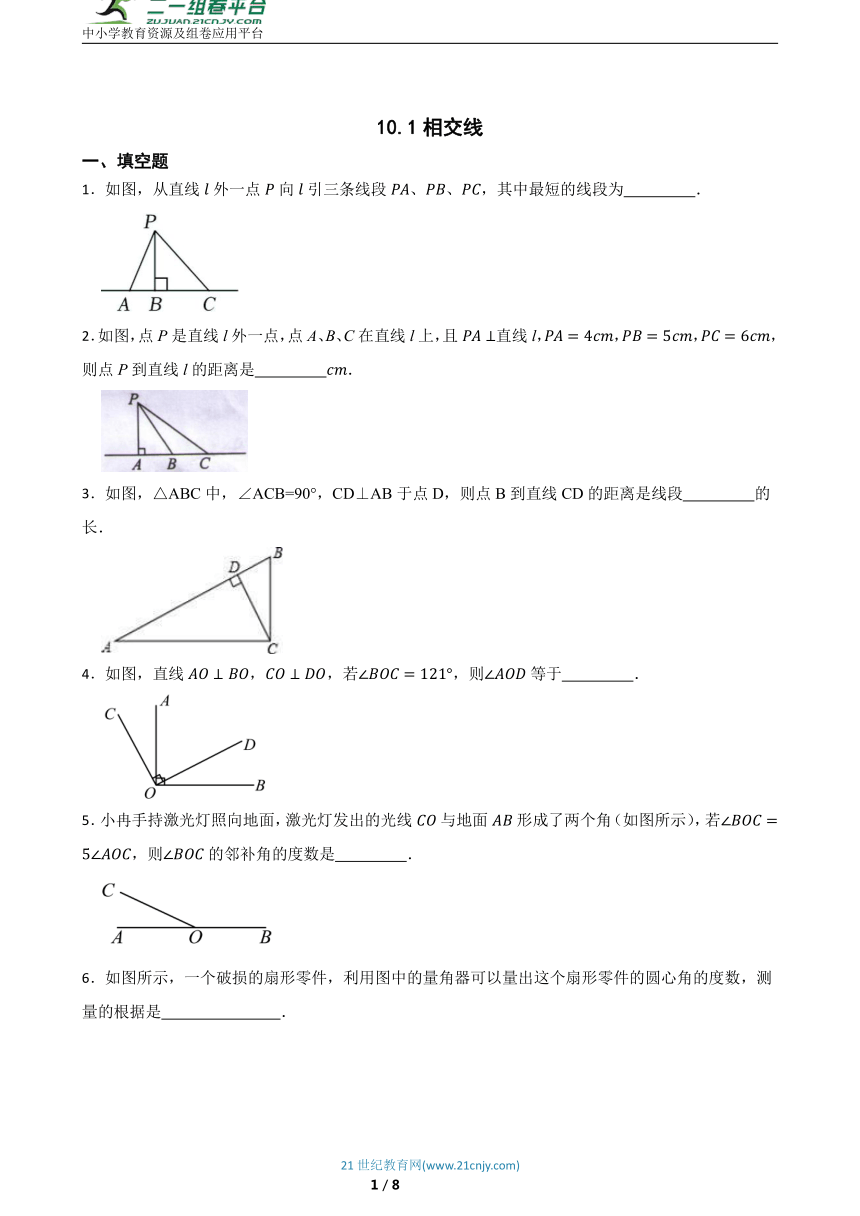
1.如图,从直线外一点向引三条线段、、,其中最短的线段为 .
2.如图,点P是直线l外一点,点A、B、C在直线l上,且直线l,,,,则点P到直线l的距离是 .
3.如图,△ABC中,∠ACB=90°,CD⊥AB于点D,则点B到直线CD的距离是线段 的长.
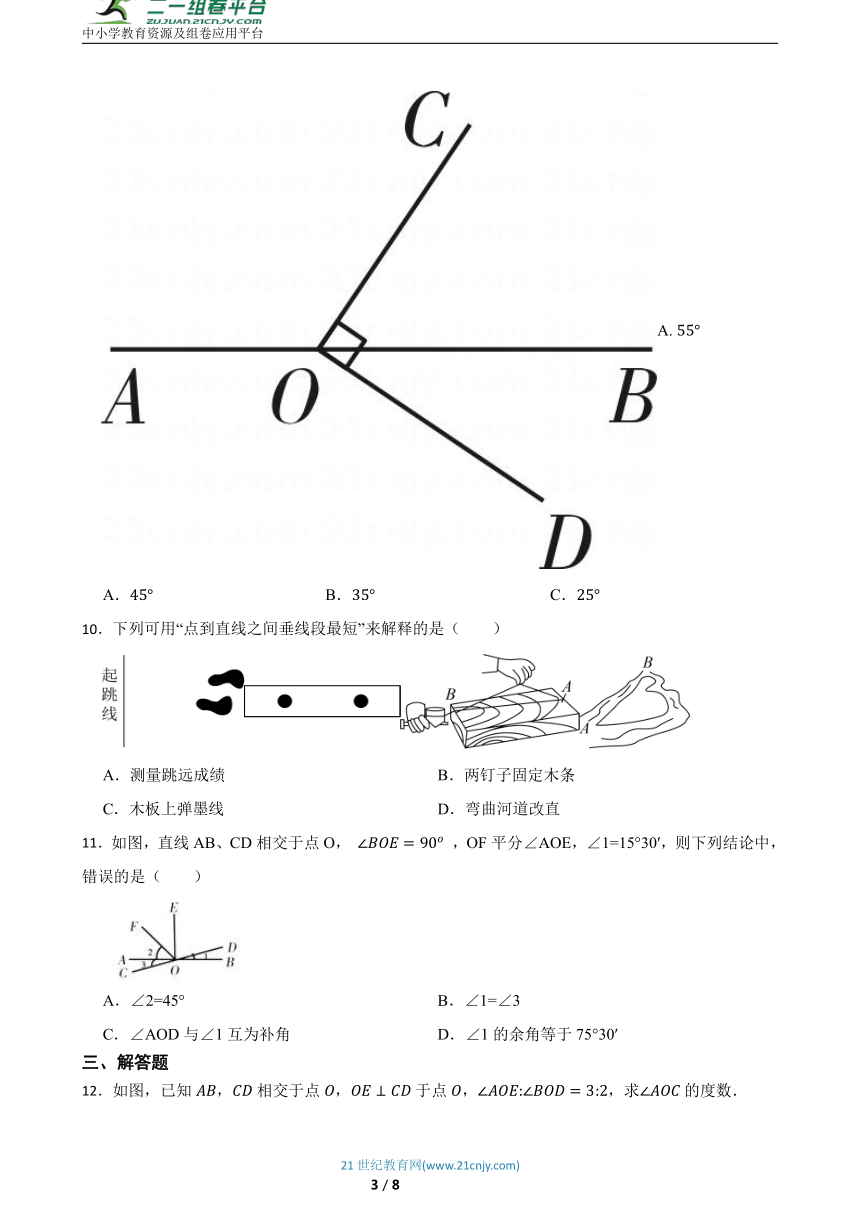
4.如图,直线,,若,则等于 .
5.小冉手持激光灯照向地面,激光灯发出的光线与地面形成了两个角(如图所示),若,则的邻补角的度数是 .
6.如图所示,一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数,测量的根据是 .
二、单选题
7.下面四幅图中,与是对顶角的是( )
A. B.
C. D.
8.如图,昭通将向“县县通高铁”的目标进发,着力构建“四横八纵两联多专用”铁路网,在铁路上修建一个站点,设计了A、B、C、D四个,为了县城P到站点的距离近,我们应选择哪个站( )
A.站点A B.站点B C.站点C D.站点D
9.如图,点在直线上,若,则等于( )
A.
A. B. C.
10.下列可用“点到直线之间垂线段最短”来解释的是( )
A.测量跳远成绩 B.两钉子固定木条
C.木板上弹墨线 D.弯曲河道改直
11.如图,直线AB、CD相交于点O, ,OF平分∠AOE,∠1=15°30′,则下列结论中,错误的是( )
A.∠2=45° B.∠1=∠3
C.∠AOD与∠1互为补角 D.∠1的余角等于75°30′
三、解答题
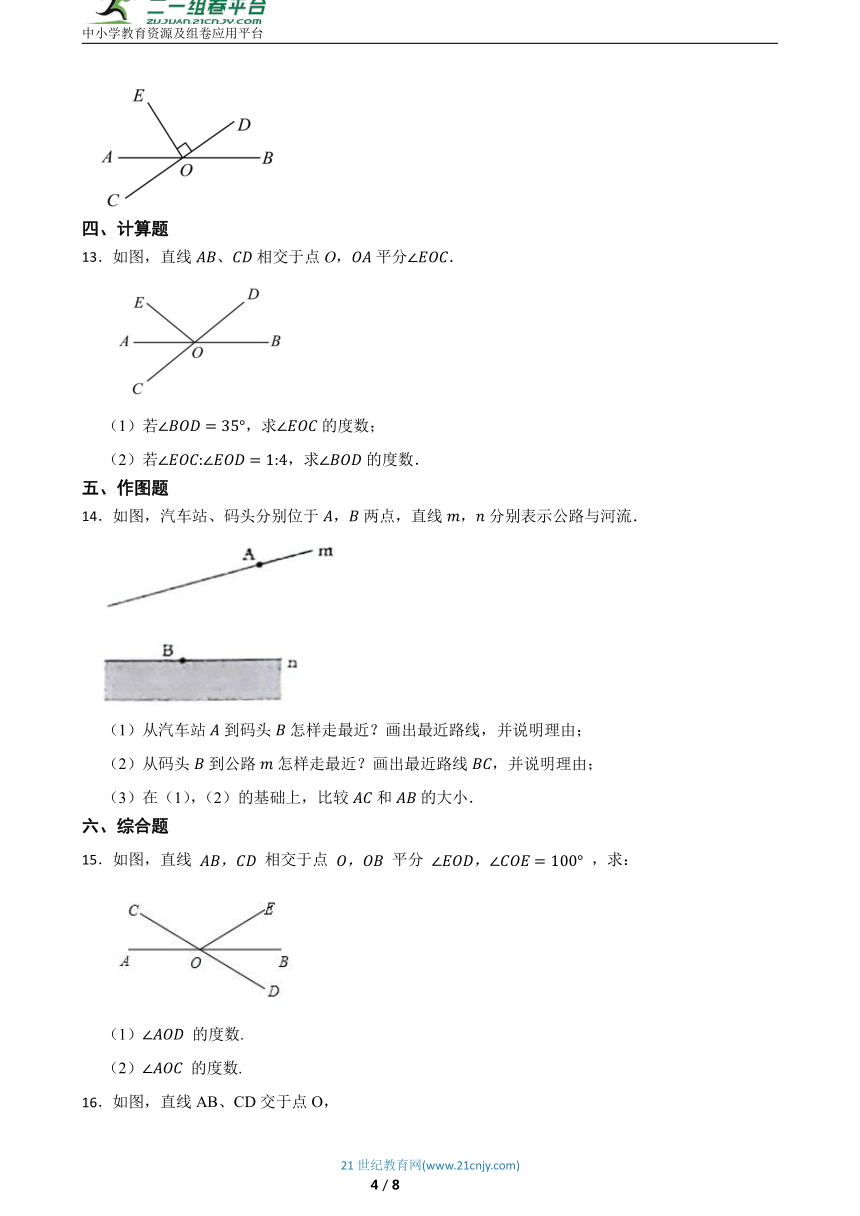
12.如图,已知,相交于点,于点,,求的度数.
四、计算题
13.如图,直线、相交于点O,平分.
(1)若,求的度数;
(2)若,求的度数.
五、作图题
14.如图,汽车站、码头分别位于,两点,直线,分别表示公路与河流.
(1)从汽车站到码头怎样走最近?画出最近路线,并说明理由;
(2)从码头到公路怎样走最近?画出最近路线,并说明理由;
(3)在(1),(2)的基础上,比较和的大小.
六、综合题
15.如图,直线 相交于点 平分 ,求:
(1) 的度数.
(2) 的度数.
16.如图,直线AB、CD交于点O,
(1)若∠AOC=90°,则AB CD.
(2)若AB⊥CD,则∠AOC= = = = 度.
17.如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE.
(1)写出∠BOE的余角;
(2)若∠COF的度数为29°,求∠BOE的度数.
七、实践探究题
18.如图,点P是直线l外的一点,画PO⊥l于O,线段PO称为点P到直线l的垂线段.点P与直线l.上所有各点之间的距离中,哪一个距离最小?你能设计一个实验来验证你的判断吗?
答案解析部分
1.【答案】PB
【知识点】垂线段最短及其应用
2.【答案】4
【知识点】点到直线的距离
3.【答案】BD
【知识点】点到直线的距离
4.【答案】
【知识点】角的运算;垂线的概念
5.【答案】
【知识点】邻补角
6.【答案】对顶角相等
【知识点】对顶角及其性质
7.【答案】A
【知识点】对顶角及其性质
8.【答案】C
【知识点】垂线段最短及其应用;点到直线的距离
9.【答案】B
【知识点】垂线的概念;邻补角
10.【答案】A
【知识点】垂线段最短及其应用
11.【答案】D
【知识点】余角、补角及其性质;对顶角及其性质;角平分线的概念
12.【答案】
【知识点】角的运算;垂线的概念;对顶角及其性质
13.【答案】(1)解:∵直线、相交于点O,,
∴,
∵平分,
∴
(2)解:∵,,
∴,
∴,
∵平分,,
∴.
【知识点】余角、补角及其性质;对顶角及其性质;角平分线的概念
14.【答案】(1)解:图见解析,连接;两点之间,线段最短
(2)解:图见解析,过点作,垂足为;垂线段最短
(3)解:
【知识点】两点之间线段最短;垂线段最短及其应用;尺规作图-直线、射线、线段
15.【答案】(1)解:∵∠ ,
∴ ,
∵OB平分 ,
∴ ,
∴
(2)解:∵ ,
∴
【知识点】对顶角及其性质;邻补角
16.【答案】(1)⊥
(2)∠COB;∠BOD;∠AOD;90
【知识点】垂线的概念
17.【答案】(1)解:∵直线AB和CD相交于点O,∠COE=90°,
∴∠BOD=∠AOC,∠DOE=90°,
∴∠BOE+∠BOD=90°,
∴∠BOE+∠AOC=90°,
∴∠BOE的余角是∠BOD和∠AOC;
(2)解:∵∠COF=29°,∠COE=90°,
∴∠EOF=90°﹣29°=61°,
又OF平分∠AOE,
∴∠AOE=122°,
∵∠BOE+∠AOE=180°,
∴∠BOE=180°﹣∠AOE=58°.
【知识点】余角、补角及其性质;对顶角及其性质;邻补角;角平分线的概念
18.【答案】解:P、O两点的距离最小;验证方法:以点P为圆心,PO为半径作圆弧,圆弧都交PA1、PA2、PA3、······、PB1、PB2、······这些线段于内部.
【知识点】垂线段最短及其应用
21世纪教育网(www.21cnjy.com)
1 / 8
10.1相交线
一、填空题
1.如图,从直线外一点向引三条线段、、,其中最短的线段为 .
2.如图,点P是直线l外一点,点A、B、C在直线l上,且直线l,,,,则点P到直线l的距离是 .
3.如图,△ABC中,∠ACB=90°,CD⊥AB于点D,则点B到直线CD的距离是线段 的长.
4.如图,直线,,若,则等于 .
5.小冉手持激光灯照向地面,激光灯发出的光线与地面形成了两个角(如图所示),若,则的邻补角的度数是 .
6.如图所示,一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数,测量的根据是 .
二、单选题
7.下面四幅图中,与是对顶角的是( )
A. B.
C. D.
8.如图,昭通将向“县县通高铁”的目标进发,着力构建“四横八纵两联多专用”铁路网,在铁路上修建一个站点,设计了A、B、C、D四个,为了县城P到站点的距离近,我们应选择哪个站( )
A.站点A B.站点B C.站点C D.站点D
9.如图,点在直线上,若,则等于( )
A.
A. B. C.
10.下列可用“点到直线之间垂线段最短”来解释的是( )
A.测量跳远成绩 B.两钉子固定木条
C.木板上弹墨线 D.弯曲河道改直
11.如图,直线AB、CD相交于点O, ,OF平分∠AOE,∠1=15°30′,则下列结论中,错误的是( )
A.∠2=45° B.∠1=∠3
C.∠AOD与∠1互为补角 D.∠1的余角等于75°30′
三、解答题
12.如图,已知,相交于点,于点,,求的度数.
四、计算题
13.如图,直线、相交于点O,平分.
(1)若,求的度数;
(2)若,求的度数.
五、作图题
14.如图,汽车站、码头分别位于,两点,直线,分别表示公路与河流.
(1)从汽车站到码头怎样走最近?画出最近路线,并说明理由;
(2)从码头到公路怎样走最近?画出最近路线,并说明理由;
(3)在(1),(2)的基础上,比较和的大小.
六、综合题
15.如图,直线 相交于点 平分 ,求:
(1) 的度数.
(2) 的度数.
16.如图,直线AB、CD交于点O,
(1)若∠AOC=90°,则AB CD.
(2)若AB⊥CD,则∠AOC= = = = 度.
17.如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE.
(1)写出∠BOE的余角;
(2)若∠COF的度数为29°,求∠BOE的度数.
七、实践探究题
18.如图,点P是直线l外的一点,画PO⊥l于O,线段PO称为点P到直线l的垂线段.点P与直线l.上所有各点之间的距离中,哪一个距离最小?你能设计一个实验来验证你的判断吗?
答案解析部分
1.【答案】PB
【知识点】垂线段最短及其应用
2.【答案】4
【知识点】点到直线的距离
3.【答案】BD
【知识点】点到直线的距离
4.【答案】
【知识点】角的运算;垂线的概念
5.【答案】
【知识点】邻补角
6.【答案】对顶角相等
【知识点】对顶角及其性质
7.【答案】A
【知识点】对顶角及其性质
8.【答案】C
【知识点】垂线段最短及其应用;点到直线的距离
9.【答案】B
【知识点】垂线的概念;邻补角
10.【答案】A
【知识点】垂线段最短及其应用
11.【答案】D
【知识点】余角、补角及其性质;对顶角及其性质;角平分线的概念
12.【答案】
【知识点】角的运算;垂线的概念;对顶角及其性质
13.【答案】(1)解:∵直线、相交于点O,,
∴,
∵平分,
∴
(2)解:∵,,
∴,
∴,
∵平分,,
∴.
【知识点】余角、补角及其性质;对顶角及其性质;角平分线的概念
14.【答案】(1)解:图见解析,连接;两点之间,线段最短
(2)解:图见解析,过点作,垂足为;垂线段最短
(3)解:
【知识点】两点之间线段最短;垂线段最短及其应用;尺规作图-直线、射线、线段
15.【答案】(1)解:∵∠ ,
∴ ,
∵OB平分 ,
∴ ,
∴
(2)解:∵ ,
∴
【知识点】对顶角及其性质;邻补角
16.【答案】(1)⊥
(2)∠COB;∠BOD;∠AOD;90
【知识点】垂线的概念
17.【答案】(1)解:∵直线AB和CD相交于点O,∠COE=90°,
∴∠BOD=∠AOC,∠DOE=90°,
∴∠BOE+∠BOD=90°,
∴∠BOE+∠AOC=90°,
∴∠BOE的余角是∠BOD和∠AOC;
(2)解:∵∠COF=29°,∠COE=90°,
∴∠EOF=90°﹣29°=61°,
又OF平分∠AOE,
∴∠AOE=122°,
∵∠BOE+∠AOE=180°,
∴∠BOE=180°﹣∠AOE=58°.
【知识点】余角、补角及其性质;对顶角及其性质;邻补角;角平分线的概念
18.【答案】解:P、O两点的距离最小;验证方法:以点P为圆心,PO为半径作圆弧,圆弧都交PA1、PA2、PA3、······、PB1、PB2、······这些线段于内部.
【知识点】垂线段最短及其应用
21世纪教育网(www.21cnjy.com)
1 / 8
