10.3平行线的性质(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
10.3平行线的性质
一、单选题
1.如图,,,则的度数为( )
A. B. C. D.
2.如图,直线与直线相交,已知,则的度数为( )
A. B. C. D.
3.下列说法中正确的是( )
A.过直线外一点有且只有一条直线与已知直线平行
B.相等的两个角一定是对顶角
C.在同一平面内,垂直于同一条直线的两直线互相垂直
D.同旁内角相等,两直线平行
4.如图,若,,则的度数为( )
A. B. C. D.
5.如图,a∥b,∠1=,则等于( )
A. B. C. D.
二、填空题
6.如图,DA⊥CE于点A,CD∥AB,∠1=30°,则∠D= .
7.如图,点B,C,D在同一条直线上,CE∥AB,,如果,那么 .
8.如图,直线a,b被直线c所截,,,则的度数为 .
9.如图,直线a∥b,直线m与a,b均相交,若∠1=38°,则∠2= .
10.如图,直线,,,则 .
11.已知:如图,点D是射线AB上一动点,连接CD,过点D作交直线AC于点E,若,,则的度数为 .
三、解答题
12.如图,在墙面上安装某一管道需经两次拐弯,拐弯后的管道与拐弯前的管道平行.若第一个弯道处∠B=142°,则第二个弯道处∠C的度数为 °.
四、计算题
13.如图, , , ,求 、 的度数.
14.如图,直线分别交直线于点G,H,射线分别在和的内部,且.
(1)若和互补.
①求的度数;
②当,且时,求的度数;
(2)设,.若,求m,n满足的等量关系.
15.在四边形ABCD中,∠BAD=∠BCD,AB∥DC,点E是射线CD上一个动点(不与C,D重合),过点E作EF∥AD,交直线AC于点F.
(1)如图,当点E在线段CD上时,求证:∠DEF=∠DCB.
(2)若点E在线段CD的延长线上,用等式表示∠DEF与∠DCB之间的数量关系是 .
五、作图题
16.请补全证明过程及推理依据.已知:如图,点,,分别是三角形的边,,上的点,若,.求证:.
证明:∵,
∴ .( )
∵,
∴,( )
∴,( )
∴.
六、综合题
17.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2) CD与EF平行吗?为什么?
(3)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
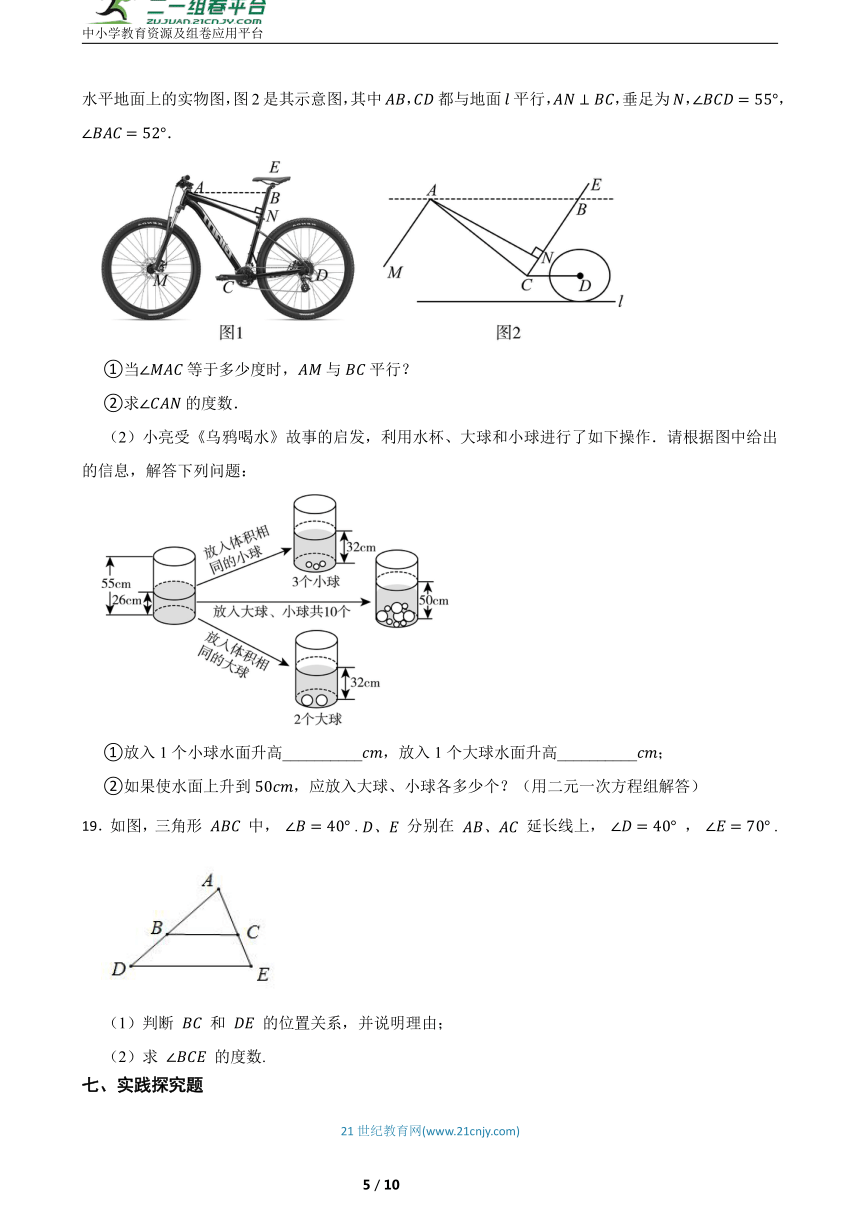
18.(1)为了方便市民绿色出行和锻炼身体,政府倡导大家使用共享单车.图1是一辆共享单车放在水平地面上的实物图,图2是其示意图,其中,都与地面平行,,垂足为,,.
①当等于多少度时,与平行?
②求的度数.
(2)小亮受《乌鸦喝水》故事的启发,利用水杯、大球和小球进行了如下操作.请根据图中给出的信息,解答下列问题:
①放入1个小球水面升高__________,放入1个大球水面升高__________;
②如果使水面上升到,应放入大球、小球各多少个?(用二元一次方程组解答)
19.如图,三角形 中, . 分别在 延长线上, , .
(1)判断 和 的位置关系,并说明理由;
(2)求 的度数.
七、实践探究题
20.综合与实践
数学课上,老师提出问题:如图,钓板上存在三条互相平行的直线,,,图1中弹性皮筋两端点用钉子固定在点,处,拉住皮筋中部的一点至点处固定,点在直线上,.若,求的度数.
数学思考:(1)完成老师提出的问题.
深入探究:(2)老师让同学们在图1的基础上,通过移动点的位置或添加皮筋的方式增设条件来提出新的问题.
①“善思小组”提出问题:如图2,在图1的基础上,将另一根弹性皮筋的一端固定在点处,另一端用钉子固定在点处.若,求的值.
②“智慧小组”提出问题:如图3,在与的交点处用钉子固定点,在与的交点处用钉子固定点,将点移动到点处(点在直线上).若,请直接写出的值.
答案解析部分
1.【答案】D
【知识点】平行线的性质;邻补角
2.【答案】D
【知识点】平行线的判定与性质
3.【答案】A
【知识点】平行线的判定与性质;对顶角及其性质
4.【答案】A
【知识点】平行线的性质;对顶角及其性质
5.【答案】C
【知识点】平行线的性质;对顶角及其性质
6.【答案】60°
【知识点】平行线的性质
7.【答案】53°或53度
【知识点】平行线的性质
8.【答案】
【知识点】常用角的度量单位及换算;角的运算;平行线的性质
9.【答案】142°
【知识点】平行线的性质
10.【答案】
【知识点】垂线的概念;平行公理及推论;平行线的性质
11.【答案】104°
【知识点】平行线的性质
12.【答案】142
【知识点】平行线的性质
13.【答案】解: ,
.
,
,
.
的度数为 , 的度数为 .
【知识点】平行线的性质
14.【答案】(1)解:①和互补,
.
,
,
;
②由①得,
,
,
又,
,
.
,
,
;
(2)解:,
.
设,
,,
,
,
又,
,
,
,
即m,n满足的等量关系为.
【知识点】角的运算;平行线的性质;邻补角
15.【答案】(1)证明:∵AB∥DC,
∴∠B+∠BCD=180°,
∵∠BAD=∠BCD,
∴∠B+∠BAD=180°,
∴AD∥BC,
∵EF∥AD,
∴EF∥BC,
∴∠DEF=∠DCB.
(2)∠DEF+∠DCB=180°
【知识点】平行线的判定与性质
16.【答案】∠B;两直线平行,同位角相等;等量代换;内错角相等,两直线平行.
【知识点】平行线的判定与性质
17.【答案】(1)解:CD与EF平行.理由如下:
CD⊥AB,EF⊥AB,
∴∠CDB=∠EFB=90°
∴EF∥CD
(2)解:CD与EF平行.理由如下:
CD⊥AB,EF⊥AB,
∴∠CDB=∠EFB=90°
∴EF∥CD
(3)解:如图:
EF∥CD,
∴∠2=∠BCD
又 ∠1=∠2,
∴∠1=∠BCD
∴DG∥BC,
∴∠ACB=∠3=115°.
【知识点】垂线的概念;平行线的判定与性质
18.【答案】(1)①,②;(2)①2,3;②放入小球6个,放入大球4个
【知识点】余角、补角及其性质;平行线的性质;二元一次方程组的实际应用-方案选择题问题
19.【答案】(1)解: .
理由如下:
,
(2)解:由(1)知, ,
∵
【知识点】平行线的判定与性质
20.【答案】(1);(2) ①,②;
【知识点】平行线的性质
21世纪教育网(www.21cnjy.com)
2 / 10
10.3平行线的性质
一、单选题
1.如图,,,则的度数为( )
A. B. C. D.
2.如图,直线与直线相交,已知,则的度数为( )
A. B. C. D.
3.下列说法中正确的是( )
A.过直线外一点有且只有一条直线与已知直线平行
B.相等的两个角一定是对顶角
C.在同一平面内,垂直于同一条直线的两直线互相垂直
D.同旁内角相等,两直线平行
4.如图,若,,则的度数为( )
A. B. C. D.
5.如图,a∥b,∠1=,则等于( )
A. B. C. D.
二、填空题
6.如图,DA⊥CE于点A,CD∥AB,∠1=30°,则∠D= .
7.如图,点B,C,D在同一条直线上,CE∥AB,,如果,那么 .
8.如图,直线a,b被直线c所截,,,则的度数为 .
9.如图,直线a∥b,直线m与a,b均相交,若∠1=38°,则∠2= .
10.如图,直线,,,则 .
11.已知:如图,点D是射线AB上一动点,连接CD,过点D作交直线AC于点E,若,,则的度数为 .
三、解答题
12.如图,在墙面上安装某一管道需经两次拐弯,拐弯后的管道与拐弯前的管道平行.若第一个弯道处∠B=142°,则第二个弯道处∠C的度数为 °.
四、计算题
13.如图, , , ,求 、 的度数.
14.如图,直线分别交直线于点G,H,射线分别在和的内部,且.
(1)若和互补.
①求的度数;
②当,且时,求的度数;
(2)设,.若,求m,n满足的等量关系.
15.在四边形ABCD中,∠BAD=∠BCD,AB∥DC,点E是射线CD上一个动点(不与C,D重合),过点E作EF∥AD,交直线AC于点F.
(1)如图,当点E在线段CD上时,求证:∠DEF=∠DCB.
(2)若点E在线段CD的延长线上,用等式表示∠DEF与∠DCB之间的数量关系是 .
五、作图题
16.请补全证明过程及推理依据.已知:如图,点,,分别是三角形的边,,上的点,若,.求证:.
证明:∵,
∴ .( )
∵,
∴,( )
∴,( )
∴.
六、综合题
17.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2) CD与EF平行吗?为什么?
(3)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
18.(1)为了方便市民绿色出行和锻炼身体,政府倡导大家使用共享单车.图1是一辆共享单车放在水平地面上的实物图,图2是其示意图,其中,都与地面平行,,垂足为,,.
①当等于多少度时,与平行?
②求的度数.
(2)小亮受《乌鸦喝水》故事的启发,利用水杯、大球和小球进行了如下操作.请根据图中给出的信息,解答下列问题:
①放入1个小球水面升高__________,放入1个大球水面升高__________;
②如果使水面上升到,应放入大球、小球各多少个?(用二元一次方程组解答)
19.如图,三角形 中, . 分别在 延长线上, , .
(1)判断 和 的位置关系,并说明理由;
(2)求 的度数.
七、实践探究题
20.综合与实践
数学课上,老师提出问题:如图,钓板上存在三条互相平行的直线,,,图1中弹性皮筋两端点用钉子固定在点,处,拉住皮筋中部的一点至点处固定,点在直线上,.若,求的度数.
数学思考:(1)完成老师提出的问题.
深入探究:(2)老师让同学们在图1的基础上,通过移动点的位置或添加皮筋的方式增设条件来提出新的问题.
①“善思小组”提出问题:如图2,在图1的基础上,将另一根弹性皮筋的一端固定在点处,另一端用钉子固定在点处.若,求的值.
②“智慧小组”提出问题:如图3,在与的交点处用钉子固定点,在与的交点处用钉子固定点,将点移动到点处(点在直线上).若,请直接写出的值.
答案解析部分
1.【答案】D
【知识点】平行线的性质;邻补角
2.【答案】D
【知识点】平行线的判定与性质
3.【答案】A
【知识点】平行线的判定与性质;对顶角及其性质
4.【答案】A
【知识点】平行线的性质;对顶角及其性质
5.【答案】C
【知识点】平行线的性质;对顶角及其性质
6.【答案】60°
【知识点】平行线的性质
7.【答案】53°或53度
【知识点】平行线的性质
8.【答案】
【知识点】常用角的度量单位及换算;角的运算;平行线的性质
9.【答案】142°
【知识点】平行线的性质
10.【答案】
【知识点】垂线的概念;平行公理及推论;平行线的性质
11.【答案】104°
【知识点】平行线的性质
12.【答案】142
【知识点】平行线的性质
13.【答案】解: ,
.
,
,
.
的度数为 , 的度数为 .
【知识点】平行线的性质
14.【答案】(1)解:①和互补,
.
,
,
;
②由①得,
,
,
又,
,
.
,
,
;
(2)解:,
.
设,
,,
,
,
又,
,
,
,
即m,n满足的等量关系为.
【知识点】角的运算;平行线的性质;邻补角
15.【答案】(1)证明:∵AB∥DC,
∴∠B+∠BCD=180°,
∵∠BAD=∠BCD,
∴∠B+∠BAD=180°,
∴AD∥BC,
∵EF∥AD,
∴EF∥BC,
∴∠DEF=∠DCB.
(2)∠DEF+∠DCB=180°
【知识点】平行线的判定与性质
16.【答案】∠B;两直线平行,同位角相等;等量代换;内错角相等,两直线平行.
【知识点】平行线的判定与性质
17.【答案】(1)解:CD与EF平行.理由如下:
CD⊥AB,EF⊥AB,
∴∠CDB=∠EFB=90°
∴EF∥CD
(2)解:CD与EF平行.理由如下:
CD⊥AB,EF⊥AB,
∴∠CDB=∠EFB=90°
∴EF∥CD
(3)解:如图:
EF∥CD,
∴∠2=∠BCD
又 ∠1=∠2,
∴∠1=∠BCD
∴DG∥BC,
∴∠ACB=∠3=115°.
【知识点】垂线的概念;平行线的判定与性质
18.【答案】(1)①,②;(2)①2,3;②放入小球6个,放入大球4个
【知识点】余角、补角及其性质;平行线的性质;二元一次方程组的实际应用-方案选择题问题
19.【答案】(1)解: .
理由如下:
,
(2)解:由(1)知, ,
∵
【知识点】平行线的判定与性质
20.【答案】(1);(2) ①,②;
【知识点】平行线的性质
21世纪教育网(www.21cnjy.com)
2 / 10
