7.2 离散型随机变量及其分布列 课件(共22张PPT)
文档属性
| 名称 | 7.2 离散型随机变量及其分布列 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第七章 随机变量及其分布
7.2 离散型随机变量及其分布列
1.通过实例,了解离散型随机变量的概念.
2.掌握离散型随机变量分布列的表示方法和性质.
3.掌握两点分布列有关知识及应用.
随机试验是指满足下列三 个条件的试验:
试验可以在相同 的情形下重复进行;
试验的所有可能结果是明确可知的 , 并 且不只一个;
每次试验总是恰好出现这些可能结果中的一个 ,但是在一次试验之前却不能肯定这次试验会出现哪一个结果。
问:什么是随机试验?
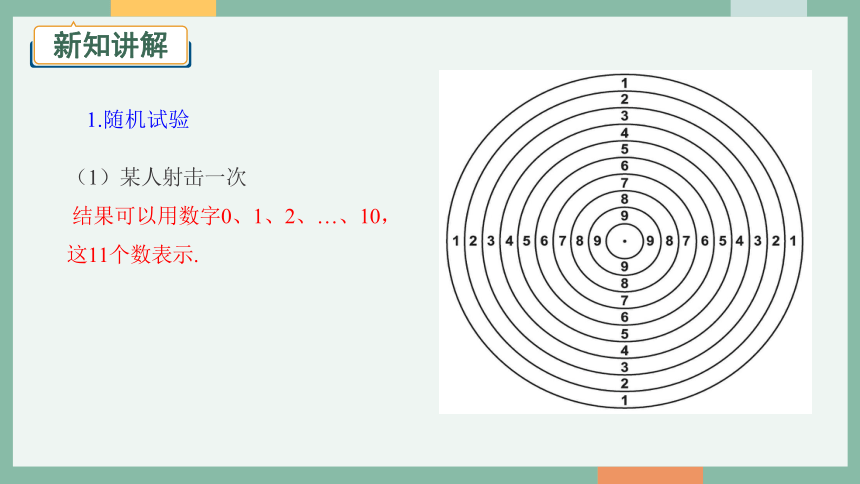
(1)某人射击一次
结果可以用数字0、1、2、… 、10,
这11个数表示.
1.随机试验
(2)抛掷一枚骰子 , 出现的点数
出现的结果可以用数字1 、2 、3 、4 、5 、6来表示.
1.随机试验
(3)工厂生产的一批产品里有次品和正品,随机抽取一件产品, 抽出的结果是否也可以用数字来表示呢?
0
1
1.随机试验
抽到次品
抽到正品
试验的结果 向上点数为1 向上点数为2 向上点数为3 向上点数为4 向上点数为5
向上点数为6
数字 1 2 3 4 5
6
试验的结果 命中0环 命中1环 命中2环 …
命中10环
数字 0 1 2 …
10
一般地,对于随机试验样本空间Ω中的每个样本点ω , 都有唯一的实数 X(ω ) 与之对 应,我们称X为随机变量.
试验的结果 抽到次品
抽到正品
数字 0
1
2.随机变量
抽产品
随机变量的概念是俄国数学家切比雪夫(Chebyshev , 1821-1894)在19世纪中叶建立和提倡使用的。
一般地,对于随机试验样本空间Ω中的每个样本点ω , 都有唯一的实数 X(ω ) 与之对 应,我们称X为随机变量.
(1)从10张已编号的卡片(从1号到10号)中任取1张, 被取出的卡片的号数X ;
(2)抛掷两个骰子,所得点数之和Y;
(3)某城市1天之中发生的火警次数X;
(4)某品牌的电灯泡的寿命X;
(5)某林场树木最高达30米,最低是0.5米,则此林场任意一棵树木的高度X .
写出下列各随机变量可能的取值 , 并说明它们各自所表示的随机试验的结果:
练一练
思考
前3个随机变量与最后两个有什么区别?
[0.5 ,30]
[0 ,+∞)
( X = 0 、1 、2 、3 、 ···)
( Y=2 、3 、 · · · 、12)
( X =1 、2 、3 、 · · · 、10)
1.如果随机变量可能取值为有限个或可以一一列举的随机变量就叫做离散型随机变量.(如掷骰子的结果 , 城市每天火警的次数等等)
2.若随机变量可以取某个区间内的一切值 , 那么这样的随机变量叫做连续型随机变量。(如灯泡的寿命 , 树木的高度等等)
寿命< 1000小时
寿命 ≥ 1000小时
0,
Y = {
1,
3.离散型随机变量
注 意
(1) 随机变量不止两种 , 我们只研究离散型随机变量;
(2) 变量离散与否与变量的选取有关;
比如: 对灯泡的寿命问题 , 可定义如下离散型随机变量.
引例:抛掷一枚质地均匀的骰子,向上一面的点数的分布列:
方法一:列表法
4.离散型随机变量的分布列
X 1 2 3 4 5
6
P 1 6 1 6 1 6 1 6 1 6
1
6
方法二:解析式法
方法三:图象法
一般地 , 若离散型随机变量X 可能取值为:x1,x2 , , xi , , xn
我们称X取每一个值xi (i= 1 , 2 , , n)的概率
P(X=xi)=Pi , i= 1 , 2 , , n
为X的概率分布列 , 简称分布列 , 以表格的表示如下:
X x1 x2 … xi
…
P P1 P2 … Pi …
分布列的性质:
(1)pi ≥ 0, i = 1, 2, . . . ; (2) pi = p1 + p2 + . . . + pn = 1
i = 1
知识归纳
D
1. 下列表中可以作为离散型随机变量的分布列是( )
X 0 1
P 2a 3a
2. 若离散型随机变量 X 的分布列如下,则a= ____.
我们称X服从两点分布或0-1分布.实际上,X为在一次实验中成功(事件A发生)的次数(0或1).像购买的彩券是否中奖,新生婴儿的性别,投放投篮是否命中等,都可以用两点分布来描述.
X 0 1
P 1-P P
两点分布
对于只有两个可能结果的随机试验,用A表示“成功 ”, A表示“失败 ”,
定义 X ={1, A发生; 如果,那么
0,A不发生
例1.一批笔记本电脑共有10台,其中A品牌3台,B品牌7台.如果从中 随机挑选2台,求这2台电脑中A品牌台数的分布列.
解: 设挑选的2台电脑中A品牌的台数为X,
则X的可能取值为0, 1 , 2.
用表格表示X的分布列,如下表所示,
例题讲解
求离散型随机变量分布列的基本步骤:
(1)确定随机变量的所有可能的值xi
( 2 )求出各取值的概率P(X=xi)=pi
( 3 )写出分布列.
定值 求概率 列表
方法归纳
例2.一袋中装有6个同样大小的小球,编号为1、2、3、4、5、6,现从中随机取出3个小球,以X表示取出球的最大号码,求X的分布列.
解:X的所有取值为:3 、4 、5 、6 .
所以随机变量X的分布列为
例题讲解
X 3 4 5
6
P 1 20 3 20 3 10
1
2
Y1 -1 1 2 0 1 2 1
3
2
P 1 12 1 4 1 3 1 12 1 6
1
12
X -2 -1 0 1 2
3
P 1 12 1 4 1 3 1 12 1 6
1
12
Y2 0 1 4
9
P 1 3 1 3 1 4
1
12
分别求出随机变量⑴ Y1 = X ;⑵ Y2 = X2 的分布列.
例3 已知随机变量X的分布列如下:
Y2 的分布列为:
解:Y1 的分布列为:
例题讲解
3.两点分布:只有两个可能结果的随机试验
4.求解离散型随机变量分布列的一般步骤
2.离散型随机变量的分布列及其性质
1.随机变量的概念
随机试验样本空间Ω中的每个样本点,都有唯一的实数X与之对应.
1. 袋中装着标有数字1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,用X表示取出的3个小球上的最大数字.
(1)取出的3个小球上的数字互不相同的概率;
(2)随机变量X的概率分布列;
(3)计算介于20分到40分之间的概率
所以随机变量X 的概率分布列为
第七章 随机变量及其分布
7.2 离散型随机变量及其分布列
1.通过实例,了解离散型随机变量的概念.
2.掌握离散型随机变量分布列的表示方法和性质.
3.掌握两点分布列有关知识及应用.
随机试验是指满足下列三 个条件的试验:
试验可以在相同 的情形下重复进行;
试验的所有可能结果是明确可知的 , 并 且不只一个;
每次试验总是恰好出现这些可能结果中的一个 ,但是在一次试验之前却不能肯定这次试验会出现哪一个结果。
问:什么是随机试验?
(1)某人射击一次
结果可以用数字0、1、2、… 、10,
这11个数表示.
1.随机试验
(2)抛掷一枚骰子 , 出现的点数
出现的结果可以用数字1 、2 、3 、4 、5 、6来表示.
1.随机试验
(3)工厂生产的一批产品里有次品和正品,随机抽取一件产品, 抽出的结果是否也可以用数字来表示呢?
0
1
1.随机试验
抽到次品
抽到正品
试验的结果 向上点数为1 向上点数为2 向上点数为3 向上点数为4 向上点数为5
向上点数为6
数字 1 2 3 4 5
6
试验的结果 命中0环 命中1环 命中2环 …
命中10环
数字 0 1 2 …
10
一般地,对于随机试验样本空间Ω中的每个样本点ω , 都有唯一的实数 X(ω ) 与之对 应,我们称X为随机变量.
试验的结果 抽到次品
抽到正品
数字 0
1
2.随机变量
抽产品
随机变量的概念是俄国数学家切比雪夫(Chebyshev , 1821-1894)在19世纪中叶建立和提倡使用的。
一般地,对于随机试验样本空间Ω中的每个样本点ω , 都有唯一的实数 X(ω ) 与之对 应,我们称X为随机变量.
(1)从10张已编号的卡片(从1号到10号)中任取1张, 被取出的卡片的号数X ;
(2)抛掷两个骰子,所得点数之和Y;
(3)某城市1天之中发生的火警次数X;
(4)某品牌的电灯泡的寿命X;
(5)某林场树木最高达30米,最低是0.5米,则此林场任意一棵树木的高度X .
写出下列各随机变量可能的取值 , 并说明它们各自所表示的随机试验的结果:
练一练
思考
前3个随机变量与最后两个有什么区别?
[0.5 ,30]
[0 ,+∞)
( X = 0 、1 、2 、3 、 ···)
( Y=2 、3 、 · · · 、12)
( X =1 、2 、3 、 · · · 、10)
1.如果随机变量可能取值为有限个或可以一一列举的随机变量就叫做离散型随机变量.(如掷骰子的结果 , 城市每天火警的次数等等)
2.若随机变量可以取某个区间内的一切值 , 那么这样的随机变量叫做连续型随机变量。(如灯泡的寿命 , 树木的高度等等)
寿命< 1000小时
寿命 ≥ 1000小时
0,
Y = {
1,
3.离散型随机变量
注 意
(1) 随机变量不止两种 , 我们只研究离散型随机变量;
(2) 变量离散与否与变量的选取有关;
比如: 对灯泡的寿命问题 , 可定义如下离散型随机变量.
引例:抛掷一枚质地均匀的骰子,向上一面的点数的分布列:
方法一:列表法
4.离散型随机变量的分布列
X 1 2 3 4 5
6
P 1 6 1 6 1 6 1 6 1 6
1
6
方法二:解析式法
方法三:图象法
一般地 , 若离散型随机变量X 可能取值为:x1,x2 , , xi , , xn
我们称X取每一个值xi (i= 1 , 2 , , n)的概率
P(X=xi)=Pi , i= 1 , 2 , , n
为X的概率分布列 , 简称分布列 , 以表格的表示如下:
X x1 x2 … xi
…
P P1 P2 … Pi …
分布列的性质:
(1)pi ≥ 0, i = 1, 2, . . . ; (2) pi = p1 + p2 + . . . + pn = 1
i = 1
知识归纳
D
1. 下列表中可以作为离散型随机变量的分布列是( )
X 0 1
P 2a 3a
2. 若离散型随机变量 X 的分布列如下,则a= ____.
我们称X服从两点分布或0-1分布.实际上,X为在一次实验中成功(事件A发生)的次数(0或1).像购买的彩券是否中奖,新生婴儿的性别,投放投篮是否命中等,都可以用两点分布来描述.
X 0 1
P 1-P P
两点分布
对于只有两个可能结果的随机试验,用A表示“成功 ”, A表示“失败 ”,
定义 X ={1, A发生; 如果,那么
0,A不发生
例1.一批笔记本电脑共有10台,其中A品牌3台,B品牌7台.如果从中 随机挑选2台,求这2台电脑中A品牌台数的分布列.
解: 设挑选的2台电脑中A品牌的台数为X,
则X的可能取值为0, 1 , 2.
用表格表示X的分布列,如下表所示,
例题讲解
求离散型随机变量分布列的基本步骤:
(1)确定随机变量的所有可能的值xi
( 2 )求出各取值的概率P(X=xi)=pi
( 3 )写出分布列.
定值 求概率 列表
方法归纳
例2.一袋中装有6个同样大小的小球,编号为1、2、3、4、5、6,现从中随机取出3个小球,以X表示取出球的最大号码,求X的分布列.
解:X的所有取值为:3 、4 、5 、6 .
所以随机变量X的分布列为
例题讲解
X 3 4 5
6
P 1 20 3 20 3 10
1
2
Y1 -1 1 2 0 1 2 1
3
2
P 1 12 1 4 1 3 1 12 1 6
1
12
X -2 -1 0 1 2
3
P 1 12 1 4 1 3 1 12 1 6
1
12
Y2 0 1 4
9
P 1 3 1 3 1 4
1
12
分别求出随机变量⑴ Y1 = X ;⑵ Y2 = X2 的分布列.
例3 已知随机变量X的分布列如下:
Y2 的分布列为:
解:Y1 的分布列为:
例题讲解
3.两点分布:只有两个可能结果的随机试验
4.求解离散型随机变量分布列的一般步骤
2.离散型随机变量的分布列及其性质
1.随机变量的概念
随机试验样本空间Ω中的每个样本点,都有唯一的实数X与之对应.
1. 袋中装着标有数字1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,用X表示取出的3个小球上的最大数字.
(1)取出的3个小球上的数字互不相同的概率;
(2)随机变量X的概率分布列;
(3)计算介于20分到40分之间的概率
所以随机变量X 的概率分布列为
