6.3.1 二项式定理 课件(共21张PPT)
文档属性
| 名称 | 6.3.1 二项式定理 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 18:02:41 | ||
图片预览







文档简介
(共21张PPT)
6.3.1 二项式定理
学习目标
1.利用计数原理分析二项式的展开过程,归纳、猜想出二项式定理,并用
计数原理加以证明;
2.会应用二项式定理求解二项展开式;
3.通过经历二项式定理的探究过程,体验“归纳、猜想、证明”的数学发
现过程,提高自己观察、分析、概括的能力,以及 “从特殊到一般”、
“从一般到特殊”等数学思想的应用能力;
4.感受二项式定理体现出的数学的内在和谐、对称美,了解相关数学史内容.
新知引入
杨辉三角
早在11世纪中国杨辉发现二项式定理,比西方早近500年左右。
在人类科学历史中,根据英国人李约瑟教授的研究,中国在人类中早期的1000多年中,在科学技术上就已经取得1000多个世界第一。
这是中国的辉煌与荣耀,也是中国快速发展崛起的重要基础。
新知引入
二项式定理,又称牛顿二项式定理,由艾萨克·牛顿于1664、1665年间提出.
牛顿善于在日常生活中思考,他取得了科学史上一个又一个重要的发现,有一次,他在向一位姑娘求婚时思想又开了小差,他脑海中只剩下了无穷量的二项式定理,他抓住了姑娘的手,错误地把它当成通烟斗的通条,硬往烟斗里塞,痛的姑娘大叫,离他而去
二项式定理在组合理论、开高次方、高阶等差数列求和,以及差分法中都有广泛的应用.
新知引入
不要盲目运算
寻找展开式规律
请同学们从项数、次数、每一项的结构特点及其系数等角度,观察上述三个展开式有什么特点?
新知引入
新知学习
可以看到,是2个相乘,只要从一个中选一项(选或),再从另一个中选一项(选或),相乘就得到展开式的一项,于是,由分步乘法计数原理,在合并同类项之前,的展开式共有=项,而且每一项都是( =0,1,2)的形式.
我们先来分析(a+b)2的展开过程,根据多项式乘法法则,
新知引入
新知学习
探究
两个盒里都有大小相同,质地相同的a、b两小球,每个盒分别取一个球,将两个球字母相乘,有几种结果?请试用分类加法计数原理进行分析.
第一类:选择0个b,结果为_______,有______个;
第二类:选择1个b,结果为_______,有______个;
第三类:选择2个b,结果为_______,有______个。
第一类:
选择0个b
第二类:
选择1个b
第三类:
选择2个b
则(a+b)2=(a+b)(a+b)
=____a2+____ab+____b2
新知引入
新知学习
类比
取
0
个
b
项
系数
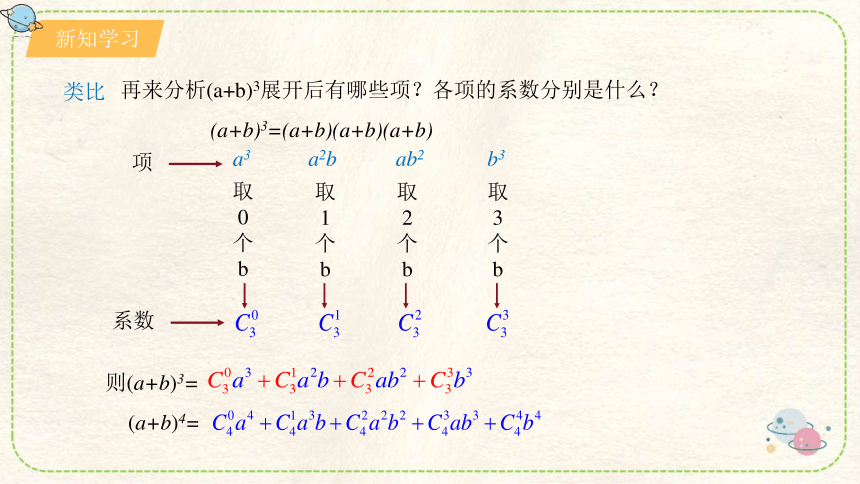
再来分析(a+b)3展开后有哪些项?各项的系数分别是什么?
取
1
个
b
取
2
个
b
取
3
个
b
(a+b)3=(a+b)(a+b)(a+b)
a3
a2b
ab2
b3
则(a+b)3=
(a+b)4=
新知引入
新知学习
仿照:
都
不
取
b
项
系数
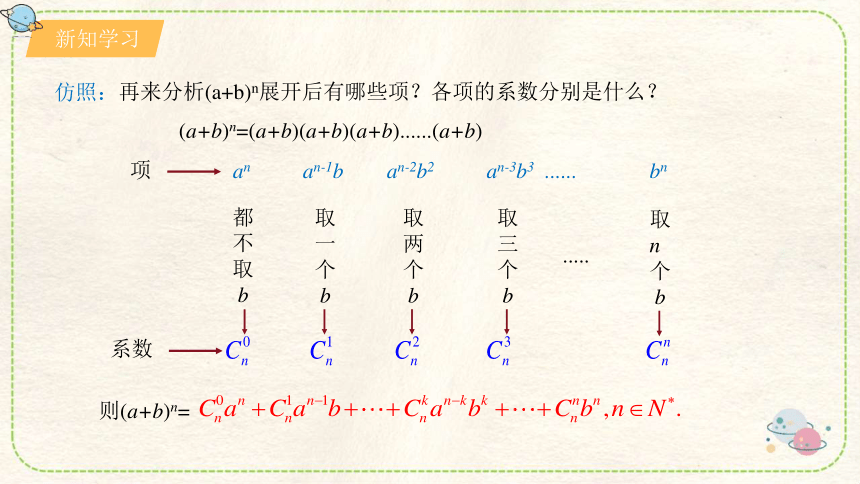
再来分析(a+b)n展开后有哪些项?各项的系数分别是什么?
取
一
个
b
取
两
个
b
取
三
个
b
取
n
个
b
(a+b)n=(a+b)(a+b)(a+b)......(a+b)
an
an-1b
an-2b2
an-3b3 ......
bn
则(a+b)n=
.....
归纳总结
追问:每一项a与b的指数和为?a的指数按什么顺序排列?b 的呢?
(a+b)n=_______________________________________________________,(1)
总结:公式(1)叫做______________,右边的多项式叫做(a+b)n的______________,
展开式中一共有______项.
其中各项的系数(k=0,1,2,…,n)叫做______________.
(a+b)n展开式的第_______项叫做二项展开式的通项,记Tk+1=_____________.
n+1
k+1
二项式定理
二项式系数
k表示?
→k表示b的指数
二项式展开式
新知引入
新知学习
二项式定理形式上的特点
(1)二项展开式有n+1项,而不是n项.
(2)二项式系数都是(k=0,1,2,…,n),它与二项展开式中某一项的系数不一定相等.
(3)二项展开式中的二项式系数的和等于2n,即.
(4)在排列方式上,按照字母a的降幂排列,从第一项起,次数由n次逐项减少1次直到0次,同时字母b按升幂排列,次数由0次逐项增加1次直到n次.
(5) 二项式定理对任意的数a, b都成立,若设a=1, b=x,则有
归纳总结
1.判断(正确的打“√”,错误的打“×”)
(1)(a+b)n展开式中共有n项. ( )
(2)在公式中,交换a,b的顺序对各项没有影响. ( )
(3)an-kbk是(a+b)n展开式中的第k项. ( )
(4)(a-b)n与(a+b)n的二项式展开式的二项式系数相同. ( )
×
×
×
√
练一练
例1
新知学习
求的展开式.
解:根据二项式定理
+
新知学习
练习1
化简.
解:
=+
==
新知学习
归纳总结
二项式定理的双向功能
(1)正用:将(a+b)n展开,得到一个多项式,即二项式定理从左到右使用是展开.对较复杂的式子,先化简再用二项式定理展开.
(2)逆用:将展开式合并成(a+b)n的形式,即二项式定理从右到左使用是合并,对于化简、求和、证明等问题的求解,要熟悉公式的特点、项数、各项幂指数的规律以及各项系数的规律.
新知学习
例2
(1)求的展开式的第4项的系数;
(2)求的展开式中的二项式系数的系数.
解:(1)的展开式的第4项是
解:(2)的展开式的通项是根据题意,得
因此,的二项式系数为:=6的系数是.
新知学习
练习1
(1)求二项式的展开式中第6项的二项式系数和第6项的系数;
(2)求的展开式中的系数.
解:(1)由已知得二项展开式的通项为,
所以第6项的二项式系数为,第6项的系数为.
解:(2)设展开式中的第项含的项,
则,
令,得,即展开式中第四项含,其系数为.
新知学习
归纳总结
要注意区分二项式系数与指定某一项的系数的差异,前者只与二项式的指数及项数有关,与二项式无关,它是一个组合数,后者与二项式、二项式的指数及项的字母和系数均有关.
随堂练习
解:
1.求 (2a+3b)6 的展开式的第3项.
2.求 的展开式的第r+1项.
解:
3.在 (x-1)(x-2)(x-3)(x-4)(x-5)的展开式中,含x4的项的系数是 .
-15
随堂练习
4. (1)求 (1+2x)7 的展开式的第4项;
(2)求 (1+2x)7 的展开式的第4项的系数;
(3)求 (1+2x)7 的展开式的第4项的二项式系数.
解:
(1)
(2)求 (1+2x)7 的展开式的第4项的系数为280.
(3)求 (1+2x)7 的展开式的第4项的二项式系数为 .
课堂小结
二项式定理
()
二项展开 公式右边的多项式
二项式系数
二项展开式的通项
注:应用通项公式的注意点
(1)是展开式中的第项,而不是第项;
(2)公式中的指数和为,且不能随便颠倒位置;
(3)要将通项中的系数和字母分离开,以便于解决问题;
(4)对二项式展开式的通项公式要特别注意符号问题.
6.3.1 二项式定理
学习目标
1.利用计数原理分析二项式的展开过程,归纳、猜想出二项式定理,并用
计数原理加以证明;
2.会应用二项式定理求解二项展开式;
3.通过经历二项式定理的探究过程,体验“归纳、猜想、证明”的数学发
现过程,提高自己观察、分析、概括的能力,以及 “从特殊到一般”、
“从一般到特殊”等数学思想的应用能力;
4.感受二项式定理体现出的数学的内在和谐、对称美,了解相关数学史内容.
新知引入
杨辉三角
早在11世纪中国杨辉发现二项式定理,比西方早近500年左右。
在人类科学历史中,根据英国人李约瑟教授的研究,中国在人类中早期的1000多年中,在科学技术上就已经取得1000多个世界第一。
这是中国的辉煌与荣耀,也是中国快速发展崛起的重要基础。
新知引入
二项式定理,又称牛顿二项式定理,由艾萨克·牛顿于1664、1665年间提出.
牛顿善于在日常生活中思考,他取得了科学史上一个又一个重要的发现,有一次,他在向一位姑娘求婚时思想又开了小差,他脑海中只剩下了无穷量的二项式定理,他抓住了姑娘的手,错误地把它当成通烟斗的通条,硬往烟斗里塞,痛的姑娘大叫,离他而去
二项式定理在组合理论、开高次方、高阶等差数列求和,以及差分法中都有广泛的应用.
新知引入
不要盲目运算
寻找展开式规律
请同学们从项数、次数、每一项的结构特点及其系数等角度,观察上述三个展开式有什么特点?
新知引入
新知学习
可以看到,是2个相乘,只要从一个中选一项(选或),再从另一个中选一项(选或),相乘就得到展开式的一项,于是,由分步乘法计数原理,在合并同类项之前,的展开式共有=项,而且每一项都是( =0,1,2)的形式.
我们先来分析(a+b)2的展开过程,根据多项式乘法法则,
新知引入
新知学习
探究
两个盒里都有大小相同,质地相同的a、b两小球,每个盒分别取一个球,将两个球字母相乘,有几种结果?请试用分类加法计数原理进行分析.
第一类:选择0个b,结果为_______,有______个;
第二类:选择1个b,结果为_______,有______个;
第三类:选择2个b,结果为_______,有______个。
第一类:
选择0个b
第二类:
选择1个b
第三类:
选择2个b
则(a+b)2=(a+b)(a+b)
=____a2+____ab+____b2
新知引入
新知学习
类比
取
0
个
b
项
系数
再来分析(a+b)3展开后有哪些项?各项的系数分别是什么?
取
1
个
b
取
2
个
b
取
3
个
b
(a+b)3=(a+b)(a+b)(a+b)
a3
a2b
ab2
b3
则(a+b)3=
(a+b)4=
新知引入
新知学习
仿照:
都
不
取
b
项
系数
再来分析(a+b)n展开后有哪些项?各项的系数分别是什么?
取
一
个
b
取
两
个
b
取
三
个
b
取
n
个
b
(a+b)n=(a+b)(a+b)(a+b)......(a+b)
an
an-1b
an-2b2
an-3b3 ......
bn
则(a+b)n=
.....
归纳总结
追问:每一项a与b的指数和为?a的指数按什么顺序排列?b 的呢?
(a+b)n=_______________________________________________________,(1)
总结:公式(1)叫做______________,右边的多项式叫做(a+b)n的______________,
展开式中一共有______项.
其中各项的系数(k=0,1,2,…,n)叫做______________.
(a+b)n展开式的第_______项叫做二项展开式的通项,记Tk+1=_____________.
n+1
k+1
二项式定理
二项式系数
k表示?
→k表示b的指数
二项式展开式
新知引入
新知学习
二项式定理形式上的特点
(1)二项展开式有n+1项,而不是n项.
(2)二项式系数都是(k=0,1,2,…,n),它与二项展开式中某一项的系数不一定相等.
(3)二项展开式中的二项式系数的和等于2n,即.
(4)在排列方式上,按照字母a的降幂排列,从第一项起,次数由n次逐项减少1次直到0次,同时字母b按升幂排列,次数由0次逐项增加1次直到n次.
(5) 二项式定理对任意的数a, b都成立,若设a=1, b=x,则有
归纳总结
1.判断(正确的打“√”,错误的打“×”)
(1)(a+b)n展开式中共有n项. ( )
(2)在公式中,交换a,b的顺序对各项没有影响. ( )
(3)an-kbk是(a+b)n展开式中的第k项. ( )
(4)(a-b)n与(a+b)n的二项式展开式的二项式系数相同. ( )
×
×
×
√
练一练
例1
新知学习
求的展开式.
解:根据二项式定理
+
新知学习
练习1
化简.
解:
=+
==
新知学习
归纳总结
二项式定理的双向功能
(1)正用:将(a+b)n展开,得到一个多项式,即二项式定理从左到右使用是展开.对较复杂的式子,先化简再用二项式定理展开.
(2)逆用:将展开式合并成(a+b)n的形式,即二项式定理从右到左使用是合并,对于化简、求和、证明等问题的求解,要熟悉公式的特点、项数、各项幂指数的规律以及各项系数的规律.
新知学习
例2
(1)求的展开式的第4项的系数;
(2)求的展开式中的二项式系数的系数.
解:(1)的展开式的第4项是
解:(2)的展开式的通项是根据题意,得
因此,的二项式系数为:=6的系数是.
新知学习
练习1
(1)求二项式的展开式中第6项的二项式系数和第6项的系数;
(2)求的展开式中的系数.
解:(1)由已知得二项展开式的通项为,
所以第6项的二项式系数为,第6项的系数为.
解:(2)设展开式中的第项含的项,
则,
令,得,即展开式中第四项含,其系数为.
新知学习
归纳总结
要注意区分二项式系数与指定某一项的系数的差异,前者只与二项式的指数及项数有关,与二项式无关,它是一个组合数,后者与二项式、二项式的指数及项的字母和系数均有关.
随堂练习
解:
1.求 (2a+3b)6 的展开式的第3项.
2.求 的展开式的第r+1项.
解:
3.在 (x-1)(x-2)(x-3)(x-4)(x-5)的展开式中,含x4的项的系数是 .
-15
随堂练习
4. (1)求 (1+2x)7 的展开式的第4项;
(2)求 (1+2x)7 的展开式的第4项的系数;
(3)求 (1+2x)7 的展开式的第4项的二项式系数.
解:
(1)
(2)求 (1+2x)7 的展开式的第4项的系数为280.
(3)求 (1+2x)7 的展开式的第4项的二项式系数为 .
课堂小结
二项式定理
()
二项展开 公式右边的多项式
二项式系数
二项展开式的通项
注:应用通项公式的注意点
(1)是展开式中的第项,而不是第项;
(2)公式中的指数和为,且不能随便颠倒位置;
(3)要将通项中的系数和字母分离开,以便于解决问题;
(4)对二项式展开式的通项公式要特别注意符号问题.
