6.3.2 二项式系数的性质 课件(共26张PPT)
文档属性
| 名称 | 6.3.2 二项式系数的性质 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
6.3.2 二项式系数的性质
学习目标
1.理解二项式系数的性质.
2.会用赋值法求展开式系数的和.
3.会用二项式定理及其性质解决有关的简单问题.
1.二项式定理
2.二项展开式的通项
3.二项式系数:
复习引入
同学们根据二项式定理写出(a+b)n(n=1,2,3,4,5,6)的二项式系数.
这个表在我国宋代数学家杨辉1261年所著的《详解九章算法》一书里就出现了,所不同的只是这里的表是用阿拉伯数字表示,在那本书里用汉字表示的,这个表称为“杨辉三角”.在欧洲,这个表被认为是法国数学家帕斯卡发现的,杨辉三角的发现比欧洲早500年左右,由此可见我国古代在数学方面的成就.
复习引入
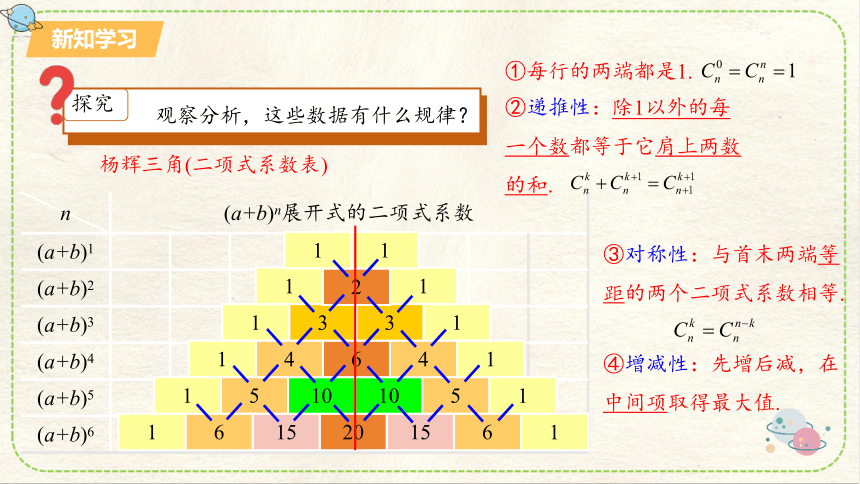
探究
观察分析,这些数据有什么规律?
n (a+b)n展开式的二项式系数 (a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
1
6
15
20
15
6
1
1
5
10
10
5
1
1
4
6
4
1
1
3
3
1
1
2
1
1
1
①每行的两端都是1.
②递推性:除1以外的每一个数都等于它肩上两数的和.
③对称性:与首末两端等距的两个二项式系数相等.
④增减性:先增后减,在中间项取得最大值.
杨辉三角(二项式系数表)
新知学习
探究
观察分析,这些数据有什么规律?
对于 展开式的二项式系数
从函数角度看, 可看成是以r为自变量的函数 ,
其定义域是
下面从函数角度分析二项式系数:
对于确定的n,我们还可以画出它的图象. 例如,当n=6时,函数 的图象是右图中的7个孤立点.
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
新知学习
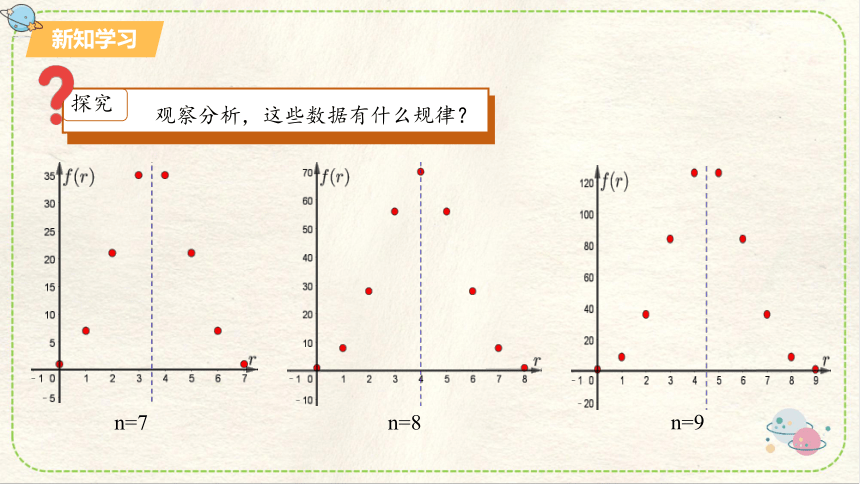
探究
观察分析,这些数据有什么规律?
n=7
n=8
n=9
新知学习
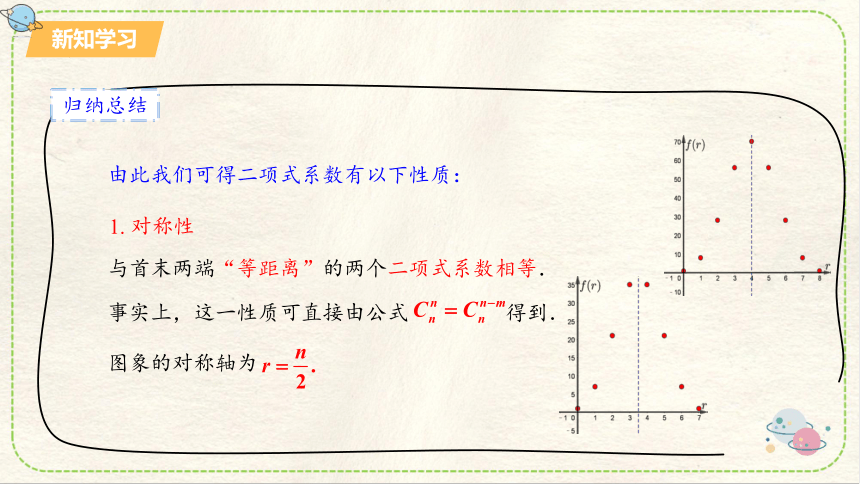
归纳总结
1. 对称性
由此我们可得二项式系数有以下性质:
与首末两端“等距离”的两个二项式系数相等.
事实上,这一性质可直接由公式 得到.
图象的对称轴为
新知学习
(1)当n为偶数时,正中间一项的二项式系数 最大;
例如:当 n=8 时, 其图象是9个孤立点,在n=4时二项式系数最大
归纳总结
2. 增减性与最大值
(2)当n为奇数时,中间两项的二项式系数 相等,且同时取得最大值.
例如:当 n=7 时, 其图象是8个孤立点,在n=3,n=4时二项式系数且最大
新知学习
所以在中间项取得最大值.
2. 增减性与最大值
归纳总结
新知学习
归纳总结
3. 各二项式系数的和
(a+b)n的展开式的各二项式系数的和等于
即
(赋值法)
证明:
新知学习
证明:
3. 各二项式系数的和
推论:
新知学习
归纳总结
一般地, 的展开式的二项式系数有如下性质:
(1)
(2)
(3)当 时,
当 时,
(4)
新知学习
练一练
例1
(1)求证:1110 -1 能被100整除;(2) 求7777-7 被19除所得的余数.
(1)证明:∵
∴ 1110 -1 能被100整除.
(2)解:
∴ 7777-7被19除所得的余数是 19-6=13.
典例解析
练习1
9192 被100除所得的余数为( )
A.1 B.81 C.-81 D.992
前91项均能被100整除,剩下两项为92×90+1=8 281,显然8 281除以100所得余数为81.
故9192被100除所得的余数为81.
解析:(90+1)92=C92(0)×9092+C92(1)×9091+…+C92(90)×902+C92(91)×90+C92(92).
练习2
设a∈Z,且0≤a<13,若512 021+a能被13整除,则a=______.
解析:∵512 021+a=(52-1)2 021+a
=522 021-522 020+522 019-…+521-1+a
所以若512 021+a能被13整除,则-1+a能被13整除,又0≤a<13,故a=1.
归纳总结
整除或余数问题的处理方法
把底数写成与除数有关的二项式,再用二项式展开式,只考虑后面的项即可,要注意余数为非负数,且小于除数.
例2
设(1-2x)2 023=a0+a1x+a2x2+…+a2 023x2 023(x∈R).
(1)求a0的值; (2)求a1+a2+a3+…+a2 023的值; (3)求a1+a3+…+a2 023的值.
解 ∵(1-2x)2 023=a0+a1x+a2x2+…+a2 023x2 023,
(1)令x=0,得(1-0)2 023=a0,因此a0=1.
(2)令x=1,得(1-2)2 023=a0+a1+a2+…+a2 023,∴a0+a1+a2+…+a2 023=-1,
因此a1+a2+…+a2 023=-2.
(3)分别令x=-1,x=1,
由②-①,得-1-32 023=2(a1+a3+…+a2 023).
典例解析
练习1
若(3x-1)7=a7x7+a6x6+…+a1x+a0.
求:(1)a1+a2+…+a7;(2)a1+a3+a5+a7; (3)|a0|+|a1|+…+|a7|.
解:(1)令x=0,则a0=-1.
令x=1,则a0+a1+…+a7=27=128,① ∴a1+a2+…+a7=129.
(2)令x=-1,得a0-a1+…+a6-a7=(-4)7,②
由①-②得,2(a1+a3+a5+a7)=128-(-4)7,∴a1+a3+a5+a7=8 256.
∴|a0|+|a1|+…+|a7|=-a0+a1-a2+a3-…-a6+a7=47=16 384.
例3
(1)求展开式中二项式系数最大的项;(2)求展开式中系数最大的项.
解: (1)令x=1,则展开式中各项系数的和为f(1)=(1+3)n=4n,
又展开式中各项的二项式系数之和为2n,
由题意知,4n-2n=992,∴(2n)2-2n-992=0,∴(2n+31)(2n-32)=0,
∴2n=-31(舍去)或2n=32,∴n=5.
由于n=5为奇数,∴展开式中二项式系数最大的项为中间的两项,
例3
(1)求展开式中二项式系数最大的项;(2)求展开式中系数最大的项.
假设Tk+1项系数最大,
∴展开式中系数最大的项为
典例解析
练习1
(1)求二项式系数最大的项;(2)系数的绝对值最大的项是第几项?(3)求系数最大的项与系数最小的项.
二项式系数最大的项为中间项,即第5项,
(2)设第r+1项系数的绝对值最大,
故系数的绝对值最大的项是第6项和第7项.
(3)由(2)知,展开式中的第6项和第7项系数的绝对值最大,第6项的系数为负,第7项的系数为正.
归纳总结
(1)二项式系数的最大项的求法
求二项式系数的最大项,根据二项式系数的性质对(a+b)n中的n进行讨论.
①当n为奇数时,中间两项的二项式系数最大.
②当n为偶数时,中间一项的二项式系数最大.
(2)展开式中系数的最大项的求法
1.已知(1+x)n的展开式中第5项和第7项的二项式系数相等,则奇数项的二项式系数和为( )
A.29 B.210 C.211 D.212
解析:由题意知=,由组合数性质得n=10,则奇数项的二项式系数和为 2n-1=29.
2.今天是星期一,今天是第1天,那么第810天是星期( )
A.一 B.二 C.三 D.四
解析:求第810天是星期几,实质是求810除以7的余数.
因为810=(7+1)10=710+×79+…+×7+1=7M+1(M∈N*),
所以第810天相当于第1天,故为星期一.
3.已知n展开式的二项式系数之和为128,求其展开式中含x3项的系数.
解:n展开式的二项式系数之和为128,所以2n=128,解得n=7.
令7-r=3,解得r=3.
随堂练习
性
质
对称性
增减性与最大值
二项式系数的和
当k<时,二项式系数是递增的
当n为奇数时,中间两项的二项式系数相等且最大
当n为偶数时,中间一项的二项式系数最大
当k>时,二项式系数时递减的
与首末两端等距的两个二项式系数相等,即
课堂小结
6.3.2 二项式系数的性质
学习目标
1.理解二项式系数的性质.
2.会用赋值法求展开式系数的和.
3.会用二项式定理及其性质解决有关的简单问题.
1.二项式定理
2.二项展开式的通项
3.二项式系数:
复习引入
同学们根据二项式定理写出(a+b)n(n=1,2,3,4,5,6)的二项式系数.
这个表在我国宋代数学家杨辉1261年所著的《详解九章算法》一书里就出现了,所不同的只是这里的表是用阿拉伯数字表示,在那本书里用汉字表示的,这个表称为“杨辉三角”.在欧洲,这个表被认为是法国数学家帕斯卡发现的,杨辉三角的发现比欧洲早500年左右,由此可见我国古代在数学方面的成就.
复习引入
探究
观察分析,这些数据有什么规律?
n (a+b)n展开式的二项式系数 (a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
1
6
15
20
15
6
1
1
5
10
10
5
1
1
4
6
4
1
1
3
3
1
1
2
1
1
1
①每行的两端都是1.
②递推性:除1以外的每一个数都等于它肩上两数的和.
③对称性:与首末两端等距的两个二项式系数相等.
④增减性:先增后减,在中间项取得最大值.
杨辉三角(二项式系数表)
新知学习
探究
观察分析,这些数据有什么规律?
对于 展开式的二项式系数
从函数角度看, 可看成是以r为自变量的函数 ,
其定义域是
下面从函数角度分析二项式系数:
对于确定的n,我们还可以画出它的图象. 例如,当n=6时,函数 的图象是右图中的7个孤立点.
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
新知学习
探究
观察分析,这些数据有什么规律?
n=7
n=8
n=9
新知学习
归纳总结
1. 对称性
由此我们可得二项式系数有以下性质:
与首末两端“等距离”的两个二项式系数相等.
事实上,这一性质可直接由公式 得到.
图象的对称轴为
新知学习
(1)当n为偶数时,正中间一项的二项式系数 最大;
例如:当 n=8 时, 其图象是9个孤立点,在n=4时二项式系数最大
归纳总结
2. 增减性与最大值
(2)当n为奇数时,中间两项的二项式系数 相等,且同时取得最大值.
例如:当 n=7 时, 其图象是8个孤立点,在n=3,n=4时二项式系数且最大
新知学习
所以在中间项取得最大值.
2. 增减性与最大值
归纳总结
新知学习
归纳总结
3. 各二项式系数的和
(a+b)n的展开式的各二项式系数的和等于
即
(赋值法)
证明:
新知学习
证明:
3. 各二项式系数的和
推论:
新知学习
归纳总结
一般地, 的展开式的二项式系数有如下性质:
(1)
(2)
(3)当 时,
当 时,
(4)
新知学习
练一练
例1
(1)求证:1110 -1 能被100整除;(2) 求7777-7 被19除所得的余数.
(1)证明:∵
∴ 1110 -1 能被100整除.
(2)解:
∴ 7777-7被19除所得的余数是 19-6=13.
典例解析
练习1
9192 被100除所得的余数为( )
A.1 B.81 C.-81 D.992
前91项均能被100整除,剩下两项为92×90+1=8 281,显然8 281除以100所得余数为81.
故9192被100除所得的余数为81.
解析:(90+1)92=C92(0)×9092+C92(1)×9091+…+C92(90)×902+C92(91)×90+C92(92).
练习2
设a∈Z,且0≤a<13,若512 021+a能被13整除,则a=______.
解析:∵512 021+a=(52-1)2 021+a
=522 021-522 020+522 019-…+521-1+a
所以若512 021+a能被13整除,则-1+a能被13整除,又0≤a<13,故a=1.
归纳总结
整除或余数问题的处理方法
把底数写成与除数有关的二项式,再用二项式展开式,只考虑后面的项即可,要注意余数为非负数,且小于除数.
例2
设(1-2x)2 023=a0+a1x+a2x2+…+a2 023x2 023(x∈R).
(1)求a0的值; (2)求a1+a2+a3+…+a2 023的值; (3)求a1+a3+…+a2 023的值.
解 ∵(1-2x)2 023=a0+a1x+a2x2+…+a2 023x2 023,
(1)令x=0,得(1-0)2 023=a0,因此a0=1.
(2)令x=1,得(1-2)2 023=a0+a1+a2+…+a2 023,∴a0+a1+a2+…+a2 023=-1,
因此a1+a2+…+a2 023=-2.
(3)分别令x=-1,x=1,
由②-①,得-1-32 023=2(a1+a3+…+a2 023).
典例解析
练习1
若(3x-1)7=a7x7+a6x6+…+a1x+a0.
求:(1)a1+a2+…+a7;(2)a1+a3+a5+a7; (3)|a0|+|a1|+…+|a7|.
解:(1)令x=0,则a0=-1.
令x=1,则a0+a1+…+a7=27=128,① ∴a1+a2+…+a7=129.
(2)令x=-1,得a0-a1+…+a6-a7=(-4)7,②
由①-②得,2(a1+a3+a5+a7)=128-(-4)7,∴a1+a3+a5+a7=8 256.
∴|a0|+|a1|+…+|a7|=-a0+a1-a2+a3-…-a6+a7=47=16 384.
例3
(1)求展开式中二项式系数最大的项;(2)求展开式中系数最大的项.
解: (1)令x=1,则展开式中各项系数的和为f(1)=(1+3)n=4n,
又展开式中各项的二项式系数之和为2n,
由题意知,4n-2n=992,∴(2n)2-2n-992=0,∴(2n+31)(2n-32)=0,
∴2n=-31(舍去)或2n=32,∴n=5.
由于n=5为奇数,∴展开式中二项式系数最大的项为中间的两项,
例3
(1)求展开式中二项式系数最大的项;(2)求展开式中系数最大的项.
假设Tk+1项系数最大,
∴展开式中系数最大的项为
典例解析
练习1
(1)求二项式系数最大的项;(2)系数的绝对值最大的项是第几项?(3)求系数最大的项与系数最小的项.
二项式系数最大的项为中间项,即第5项,
(2)设第r+1项系数的绝对值最大,
故系数的绝对值最大的项是第6项和第7项.
(3)由(2)知,展开式中的第6项和第7项系数的绝对值最大,第6项的系数为负,第7项的系数为正.
归纳总结
(1)二项式系数的最大项的求法
求二项式系数的最大项,根据二项式系数的性质对(a+b)n中的n进行讨论.
①当n为奇数时,中间两项的二项式系数最大.
②当n为偶数时,中间一项的二项式系数最大.
(2)展开式中系数的最大项的求法
1.已知(1+x)n的展开式中第5项和第7项的二项式系数相等,则奇数项的二项式系数和为( )
A.29 B.210 C.211 D.212
解析:由题意知=,由组合数性质得n=10,则奇数项的二项式系数和为 2n-1=29.
2.今天是星期一,今天是第1天,那么第810天是星期( )
A.一 B.二 C.三 D.四
解析:求第810天是星期几,实质是求810除以7的余数.
因为810=(7+1)10=710+×79+…+×7+1=7M+1(M∈N*),
所以第810天相当于第1天,故为星期一.
3.已知n展开式的二项式系数之和为128,求其展开式中含x3项的系数.
解:n展开式的二项式系数之和为128,所以2n=128,解得n=7.
令7-r=3,解得r=3.
随堂练习
性
质
对称性
增减性与最大值
二项式系数的和
当k<时,二项式系数是递增的
当n为奇数时,中间两项的二项式系数相等且最大
当n为偶数时,中间一项的二项式系数最大
当k>时,二项式系数时递减的
与首末两端等距的两个二项式系数相等,即
课堂小结
