7.2 离散型随机变量及其分布列 课件(共22张PPT)
文档属性
| 名称 | 7.2 离散型随机变量及其分布列 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 980.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
7.2 离散型随机变量及其分布列
第七章 随机变量及其分布
1.理解随机变量及离散型随机变量的含义.
2.掌握离散型随机变量分布列的表示方法和性质.
3.掌握两点分布列的有关知识及应用.
1.随机试验
随机试验是指满足下列三个条件的试验:
(1)试验可以在相同条件下重复进行;
(2)每次试验的所有可能结果都是明确可知的,并且不止一个;
(3)每次试验总是恰好出现这些结果中的一个,但在一次试验之前却不能肯定这次试验会出现哪一个结果。
我们把随机试验E的每个可能的基本结果称为样本点,全体样本点的集合称为试验E的样本空间. 我们用Ω表示样本空间,用ω表示样本点.
2.样本点与样本空间的概念
复习回顾
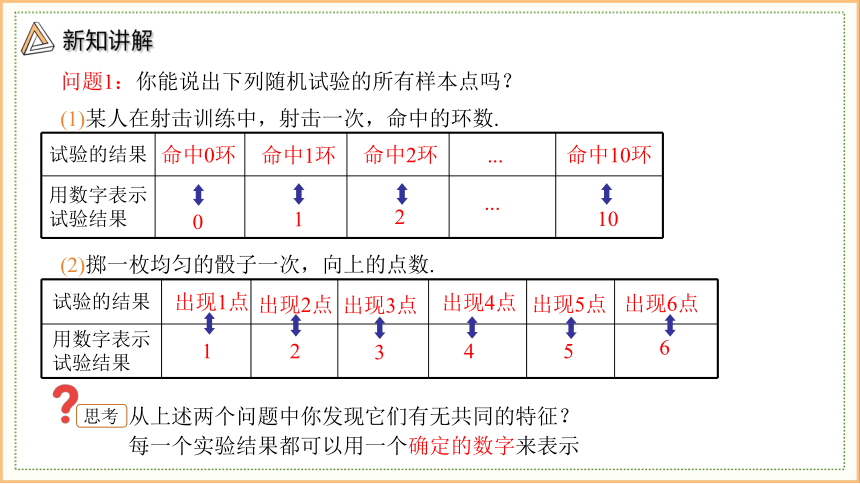
问题1:你能说出下列随机试验的所有样本点吗?
(1)某人在射击训练中,射击一次,命中的环数.
试验的结果
用数字表示试验结果
命中0环
命中1环
命中2环
命中10环
0
1
2
10
...
...
(2)掷一枚均匀的骰子一次,向上的点数.
试验的结果
用数字表示试验结果
出现1点
出现2点
出现3点
出现4点
出现5点
1
2
3
4
5
出现6点
6
从上述两个问题中你发现它们有无共同的特征?
每一个实验结果都可以用一个确定的数字来表示
思考
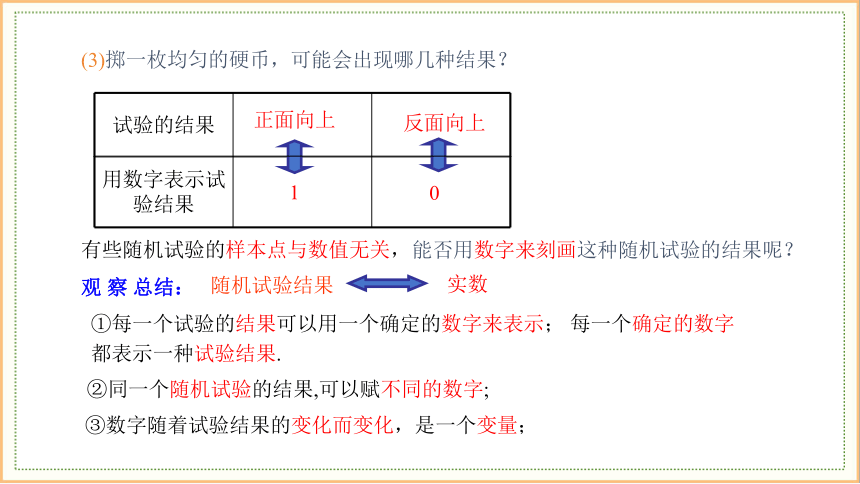
(3)掷一枚均匀的硬币,可能会出现哪几种结果?
试验的结果
正面向上
反面向上
能否用数字来刻画这种随机试验的结果呢?
有些随机试验的样本点与数值无关,
用数字表示试验结果
1
0
观 察 总结:
随机试验结果
实数
①每一个试验的结果可以用一个确定的数字来表示; 每一个确定的数字都表示一种试验结果.
②同一个随机试验的结果,可以赋不同的数字;
③数字随着试验结果的变化而变化,是一个变量;
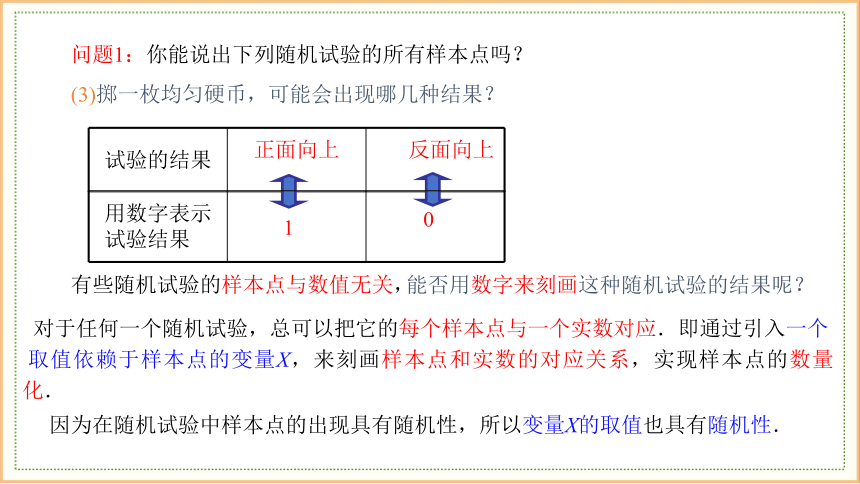
问题1:你能说出下列随机试验的所有样本点吗?
(3)掷一枚均匀硬币,可能会出现哪几种结果?
试验的结果
正面向上
反面向上
能否用数字来刻画这种随机试验的结果呢?
有些随机试验的样本点与数值无关,
用数字表示试验结果
1
0
对于任何一个随机试验,总可以把它的每个样本点与一个实数对应.即通过引入一个
取值依赖于样本点的变量X,来刻画样本点和实数的对应关系,实现样本点的数量化.
因为在随机试验中样本点的出现具有随机性,所以变量X的取值也具有随机性.
问题2:你能说出下列随机试验中引入的变量的取值吗?
试验1:从100个电子元件(至少含3个以上次品)中随机抽取三个进行检验,变量X表示三个元件中的次品数;
试验2:抛掷一枚硬币直到出现正面为止,变量Y表示需要的抛掷次数.
X=0,1,2,3
Y=1,2,3,4,…
问题3: 以上两个试验中的变量X,Y 有哪些共同的特征
在上面两个随机试验中,每个样本点都有唯一的一个实数与之对应.
变量X,Y 有如下共同点:
(1)取值依赖于样本点;
(2)所有可能取值是明确的.
一般地,对于随机试验样本空间Ω中的每个样本点w,都有唯一的实数X(w)与之对应,则称X为随机变量.
(1)随机变量的特点:①取值依赖于样本点;②所有可能取值是明确的.
(2)随机变量的表示:大写英文字母如X, Y, Z
(3)随机变量的作用:对随机试验的结果 “数量化” 。
随机变量的取值用小写英文字母如m, x, y, z
一、随机变量
二.离散型随机变量
试验1:从100个电子元件(至少含3个以上次品)中随机抽取三个进行检验,变量X表示三个元件中的次品数;
试验2:抛掷一枚硬币直到出现正面为止,变量Y表示需要的抛掷次数.
X=0,1,2,3
Y=1,2,3,4,…
试验 1 中随机变量X 的可能取值为 0, 1, 2, 3,共有 4 个值;
试验 2 中随机变量 Y 的可能取值为 1, 2, 3,,有无限个取值,但可以一一列举出来.
像这样,可能取值为有限个或可以一一列举的随机变量,我们称为离散型随机变量.
问题4: 某一自动装置无故障运转的时间X.
问题5: 某林场树木最高达 30 m,则此林场树木的高度Y,
Y是一个随机变量,它可以取区间 (0,30]内的一切值.
在问题4的无故障运转时间、问题5的树木高度等例子中,随机变量可以取某一区间内的一切值.
三.连续型随机变量
可能取值充满了某个区间、不能一一列举的随机变量称为连续型随机变量。
本节我们只研究取有限个值的离散型随机变量.
X 是一个随机变量,它可以取区间 (0,+∞)内的一切值.
问题6:若用X表示掷一枚质地均匀的骰子所掷出的点数,请确定X的可能取值及相应的概率,填入下表.
问题7:依据上表求下列事件发生的概率.
(1){X是偶数}; (2) {X≤2};
X
P
1 2 3 4 5 6
若离散型随机变量X的可能取值为:x1,x2,…,xi,…,xn,则称X取每一个xi (i=1,2,…,n)的概率P(X=xi)=pi,i=1,2,…,n为X的(概率)分布列.
X x1 x2 … xi … xn
P p1 p2 … pi … pn
离散型随机变量X的(概率)分布列也可以用表格或图形表示:
X的可能取值
每个取值的概率
离散型随机变量分布列的性质:
四、(概率)分布列
例1. 一批产品中的次品率为5%,随机抽取1件,定义,求的分布列.
解:依题意得,X的分布列为:P(X=0)=0.95,P(X=1)=0.05.
还可用表格表示为:
对于只有两个可能结果的随机试验,用表示“成功”,表示“失败”,定义
如果,,则的分布列如表所示.
我们称服从两点分布或分布.
像购买的彩券是否中奖,新生婴儿的性别,投篮是否命中等,
都可以用两点分布来描述.
在有多个结果的随机试验中,如果我们只关心一个随机事件是否发生,
就可以利用两点分布来研究它.
五、两点分布或0-1分布
例2.某学校高二年级有200名学生,他们的体育综合测试成绩分5个等级,每个等级对应的分数和人数如表所示.从这200名学生中任意选取1人,求所选同学分数X的分布列,以及P(X≥4).
等级 不及格 及格 中等 良 优
分数 1 2 3 4 5
人数 20 50 60 40 30
解:令{X=1}=“不及格”,{X=2}=“及格”,{X=3}=“中等”,{X=4}=“良”,{X=5}=“优”,则X的可能取值为1,2,3,4,5.
根据古典概型的知识,可得X的分布列如下:
例3.一批笔记本电脑共有10台,其中A品牌3台,B品牌7台. 如果从中随机挑选2台,求这两台电脑中A品牌台数的分布列.
解:设挑选的2台电脑中A品牌的台数为X,则X的可能取值为0,1,2.
根据古典概型的知识,可得X的分布列为:
用表格表示的分布列如下:
(1)确定的所有可能取值以及每个取值的意义;
(2)利用概率的相关知识,求出每个取值相应的概率;
(3)写出分布列(可用表格);
(4)根据分布列的性质对结果进行检验.
归纳总结
求离散型随机变量分布列的步骤
[练习1]一袋中装有6个同样大小的黑球,编号为1,2,3,4,5,6,现从中随机取出3个球,以X表示取出球的最大号码.
(1)求X的分布列; (2)求X的取值不小于4的概率.
解:(1)设随机变量的可能取值为3,4,5,6,,
∴随机变量的分布列如右图所示:
(2)的取值不小于4的概率为
.
[练习2]袋中有1个白球和4个黑球,每次从中任取一个球,每次取出的黑球不再放回,直到取出白球为止,求取球次数X的分布列.
解:的可能取值为1,2,3,4,5.
则第1次取到白球的概率为,
第2次取到白球的概率为,
第3次取到白球的概率为,
第4次取到白球的概率为,
5次取到白球的概率为.
∴的分布列为:
练习3:老师要从10篇课文中随机抽3篇不同的课文让同学背诵,规定至少要背出其中2篇才能及格.某位同学只能背诵其中的6篇,求:
(1)抽到他能背诵的课文的数量的分布列;(2)他能及格的概率.
解:设随机抽3篇中抽到他能背诵的课文的数量为X,
则X的可能取值为0,1,2,3,
∴X的分布列为:
练习4:某种资格证考试,每位考生一年内最多有3次考试机会.一旦某次考试通过,便可领取资格证书,不再参加以后的考试,否则就继续参加考试,直到用完3次机会.李明决定参加考试,如果他每次参加考试通过的概率依次为0.6,0.7,0.8,且每次考试是否通过相互独立,试求:
(1)李明在一年内参加考试次数X的分布列;(2)李明在一年内领到资格证书的概率.
解:X的可能取值为1,2,3,记Ai=“李明第i次考试通过(i=1,2)”,则A1与A2相互独立.
∴X的分布列为:
3.两点分布:只有两个可能结果的随机试验
4.求解离散型随机变量分布列的一般步骤
2.离散型随机变量的分布列及其性质
1.随机变量的概念
随机试验样本空间Ω中的每个样本点,都有唯一的实数X与之对应.
本节课你学到了哪些知识?
7.2 离散型随机变量及其分布列
第七章 随机变量及其分布
1.理解随机变量及离散型随机变量的含义.
2.掌握离散型随机变量分布列的表示方法和性质.
3.掌握两点分布列的有关知识及应用.
1.随机试验
随机试验是指满足下列三个条件的试验:
(1)试验可以在相同条件下重复进行;
(2)每次试验的所有可能结果都是明确可知的,并且不止一个;
(3)每次试验总是恰好出现这些结果中的一个,但在一次试验之前却不能肯定这次试验会出现哪一个结果。
我们把随机试验E的每个可能的基本结果称为样本点,全体样本点的集合称为试验E的样本空间. 我们用Ω表示样本空间,用ω表示样本点.
2.样本点与样本空间的概念
复习回顾
问题1:你能说出下列随机试验的所有样本点吗?
(1)某人在射击训练中,射击一次,命中的环数.
试验的结果
用数字表示试验结果
命中0环
命中1环
命中2环
命中10环
0
1
2
10
...
...
(2)掷一枚均匀的骰子一次,向上的点数.
试验的结果
用数字表示试验结果
出现1点
出现2点
出现3点
出现4点
出现5点
1
2
3
4
5
出现6点
6
从上述两个问题中你发现它们有无共同的特征?
每一个实验结果都可以用一个确定的数字来表示
思考
(3)掷一枚均匀的硬币,可能会出现哪几种结果?
试验的结果
正面向上
反面向上
能否用数字来刻画这种随机试验的结果呢?
有些随机试验的样本点与数值无关,
用数字表示试验结果
1
0
观 察 总结:
随机试验结果
实数
①每一个试验的结果可以用一个确定的数字来表示; 每一个确定的数字都表示一种试验结果.
②同一个随机试验的结果,可以赋不同的数字;
③数字随着试验结果的变化而变化,是一个变量;
问题1:你能说出下列随机试验的所有样本点吗?
(3)掷一枚均匀硬币,可能会出现哪几种结果?
试验的结果
正面向上
反面向上
能否用数字来刻画这种随机试验的结果呢?
有些随机试验的样本点与数值无关,
用数字表示试验结果
1
0
对于任何一个随机试验,总可以把它的每个样本点与一个实数对应.即通过引入一个
取值依赖于样本点的变量X,来刻画样本点和实数的对应关系,实现样本点的数量化.
因为在随机试验中样本点的出现具有随机性,所以变量X的取值也具有随机性.
问题2:你能说出下列随机试验中引入的变量的取值吗?
试验1:从100个电子元件(至少含3个以上次品)中随机抽取三个进行检验,变量X表示三个元件中的次品数;
试验2:抛掷一枚硬币直到出现正面为止,变量Y表示需要的抛掷次数.
X=0,1,2,3
Y=1,2,3,4,…
问题3: 以上两个试验中的变量X,Y 有哪些共同的特征
在上面两个随机试验中,每个样本点都有唯一的一个实数与之对应.
变量X,Y 有如下共同点:
(1)取值依赖于样本点;
(2)所有可能取值是明确的.
一般地,对于随机试验样本空间Ω中的每个样本点w,都有唯一的实数X(w)与之对应,则称X为随机变量.
(1)随机变量的特点:①取值依赖于样本点;②所有可能取值是明确的.
(2)随机变量的表示:大写英文字母如X, Y, Z
(3)随机变量的作用:对随机试验的结果 “数量化” 。
随机变量的取值用小写英文字母如m, x, y, z
一、随机变量
二.离散型随机变量
试验1:从100个电子元件(至少含3个以上次品)中随机抽取三个进行检验,变量X表示三个元件中的次品数;
试验2:抛掷一枚硬币直到出现正面为止,变量Y表示需要的抛掷次数.
X=0,1,2,3
Y=1,2,3,4,…
试验 1 中随机变量X 的可能取值为 0, 1, 2, 3,共有 4 个值;
试验 2 中随机变量 Y 的可能取值为 1, 2, 3,,有无限个取值,但可以一一列举出来.
像这样,可能取值为有限个或可以一一列举的随机变量,我们称为离散型随机变量.
问题4: 某一自动装置无故障运转的时间X.
问题5: 某林场树木最高达 30 m,则此林场树木的高度Y,
Y是一个随机变量,它可以取区间 (0,30]内的一切值.
在问题4的无故障运转时间、问题5的树木高度等例子中,随机变量可以取某一区间内的一切值.
三.连续型随机变量
可能取值充满了某个区间、不能一一列举的随机变量称为连续型随机变量。
本节我们只研究取有限个值的离散型随机变量.
X 是一个随机变量,它可以取区间 (0,+∞)内的一切值.
问题6:若用X表示掷一枚质地均匀的骰子所掷出的点数,请确定X的可能取值及相应的概率,填入下表.
问题7:依据上表求下列事件发生的概率.
(1){X是偶数}; (2) {X≤2};
X
P
1 2 3 4 5 6
若离散型随机变量X的可能取值为:x1,x2,…,xi,…,xn,则称X取每一个xi (i=1,2,…,n)的概率P(X=xi)=pi,i=1,2,…,n为X的(概率)分布列.
X x1 x2 … xi … xn
P p1 p2 … pi … pn
离散型随机变量X的(概率)分布列也可以用表格或图形表示:
X的可能取值
每个取值的概率
离散型随机变量分布列的性质:
四、(概率)分布列
例1. 一批产品中的次品率为5%,随机抽取1件,定义,求的分布列.
解:依题意得,X的分布列为:P(X=0)=0.95,P(X=1)=0.05.
还可用表格表示为:
对于只有两个可能结果的随机试验,用表示“成功”,表示“失败”,定义
如果,,则的分布列如表所示.
我们称服从两点分布或分布.
像购买的彩券是否中奖,新生婴儿的性别,投篮是否命中等,
都可以用两点分布来描述.
在有多个结果的随机试验中,如果我们只关心一个随机事件是否发生,
就可以利用两点分布来研究它.
五、两点分布或0-1分布
例2.某学校高二年级有200名学生,他们的体育综合测试成绩分5个等级,每个等级对应的分数和人数如表所示.从这200名学生中任意选取1人,求所选同学分数X的分布列,以及P(X≥4).
等级 不及格 及格 中等 良 优
分数 1 2 3 4 5
人数 20 50 60 40 30
解:令{X=1}=“不及格”,{X=2}=“及格”,{X=3}=“中等”,{X=4}=“良”,{X=5}=“优”,则X的可能取值为1,2,3,4,5.
根据古典概型的知识,可得X的分布列如下:
例3.一批笔记本电脑共有10台,其中A品牌3台,B品牌7台. 如果从中随机挑选2台,求这两台电脑中A品牌台数的分布列.
解:设挑选的2台电脑中A品牌的台数为X,则X的可能取值为0,1,2.
根据古典概型的知识,可得X的分布列为:
用表格表示的分布列如下:
(1)确定的所有可能取值以及每个取值的意义;
(2)利用概率的相关知识,求出每个取值相应的概率;
(3)写出分布列(可用表格);
(4)根据分布列的性质对结果进行检验.
归纳总结
求离散型随机变量分布列的步骤
[练习1]一袋中装有6个同样大小的黑球,编号为1,2,3,4,5,6,现从中随机取出3个球,以X表示取出球的最大号码.
(1)求X的分布列; (2)求X的取值不小于4的概率.
解:(1)设随机变量的可能取值为3,4,5,6,,
∴随机变量的分布列如右图所示:
(2)的取值不小于4的概率为
.
[练习2]袋中有1个白球和4个黑球,每次从中任取一个球,每次取出的黑球不再放回,直到取出白球为止,求取球次数X的分布列.
解:的可能取值为1,2,3,4,5.
则第1次取到白球的概率为,
第2次取到白球的概率为,
第3次取到白球的概率为,
第4次取到白球的概率为,
5次取到白球的概率为.
∴的分布列为:
练习3:老师要从10篇课文中随机抽3篇不同的课文让同学背诵,规定至少要背出其中2篇才能及格.某位同学只能背诵其中的6篇,求:
(1)抽到他能背诵的课文的数量的分布列;(2)他能及格的概率.
解:设随机抽3篇中抽到他能背诵的课文的数量为X,
则X的可能取值为0,1,2,3,
∴X的分布列为:
练习4:某种资格证考试,每位考生一年内最多有3次考试机会.一旦某次考试通过,便可领取资格证书,不再参加以后的考试,否则就继续参加考试,直到用完3次机会.李明决定参加考试,如果他每次参加考试通过的概率依次为0.6,0.7,0.8,且每次考试是否通过相互独立,试求:
(1)李明在一年内参加考试次数X的分布列;(2)李明在一年内领到资格证书的概率.
解:X的可能取值为1,2,3,记Ai=“李明第i次考试通过(i=1,2)”,则A1与A2相互独立.
∴X的分布列为:
3.两点分布:只有两个可能结果的随机试验
4.求解离散型随机变量分布列的一般步骤
2.离散型随机变量的分布列及其性质
1.随机变量的概念
随机试验样本空间Ω中的每个样本点,都有唯一的实数X与之对应.
本节课你学到了哪些知识?
