高中数学新课标人教A版选修2-1:2.3.2 双曲线的简单几何性质 第2课时 双曲线方程及性质的应用 课件(共20张ppt)
文档属性
| 名称 | 高中数学新课标人教A版选修2-1:2.3.2 双曲线的简单几何性质 第2课时 双曲线方程及性质的应用 课件(共20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 664.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-22 11:39:44 | ||
图片预览








文档简介
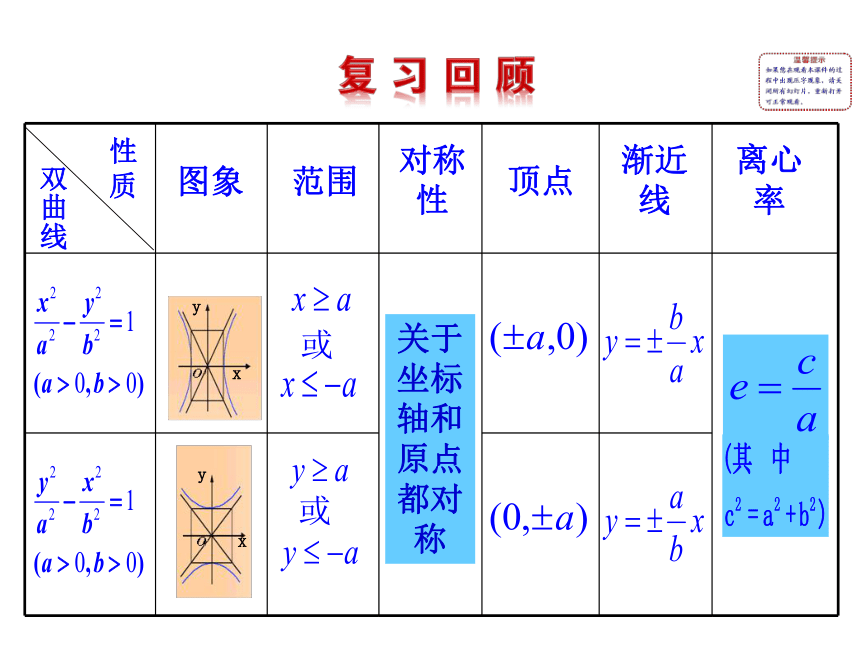
课件20张PPT。第2课时 双曲线方程及性质的应用 或或关于坐标
轴和
原点
都对
称性质双曲线范围对称
性 顶点 渐近
线离心
率图象xyxy1.了解双曲线的几何性质,并会应用于实际问
题之中.(重点)
2.会利用双曲线的定义、标准方程、几何性质
及图形四者之间的内在联系,分析和解决实
际问题.(重点、难点)探究点1 由双曲线的性质求双曲线方程已知双曲线的几何性质,求其标准方程的方法步骤:
(1)确定焦点所在的位置,以确定双曲线方程的形式;
(2)确立关于a,b,c的方程(组),求出参数a,b,c;
(3)写出标准方程.【提升总结】解:【例2】点M(x,y)与定点F(5,0)的距离和它到定
直线 的距离的比是常数 ,求点M的轨迹.xy..FOM.双曲线中应注意的几个问题:
(1)双曲线是两支曲线,而椭圆是一条封闭的曲线;
(2)双曲线的两条渐近线是区别于其他圆锥曲线所特有的;
(3)双曲线只有两个顶点,离心率e>1;
(5)注意双曲线中a,b,c,e的等量关系与椭圆中a,b,c,e的不同.【提升总结】种类: 相离; 相切; 相交(一个交点, 两个交点)探究点2 直线与双曲线的位置关系1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与双曲线的方程,
消元得到一元二次方程(当二次项系数不为0时)
(1)△>0?直线与双曲线相交?有两个公共点;
(2)△=0 ?直线与双曲线相切?有且只有一个
公共点;
(3)△<0 ?直线与双曲线相离?无公共点.通法【提升总结】直线与双曲线的位置关系:解:由双曲线的方程得,两焦点分别为F1(-3,0),F2(3,0). 因为直线AB的倾斜角是30°,且直线经过右焦点F2,所以,直线AB的方程为【提升总结】这里我们也可以利用弦长公式求解.弦长公式:或算一算,看结果一样吗?【变式练习】解析:因为F1的坐标是(-3,0),所以92.过双曲线的一个焦点F2作垂直于实轴的弦PQ,点
F1是另一个焦点,若∠PF1Q=90°,则双曲线的离
心率等于________.C4.求一条渐近线方程是3x+4y=0,一个焦点是(4,0)的双曲线标准方程.
解析:因为双曲线的一条渐近线方程为3x+4y=0,1.双曲线的简单几何性质,利用性质求方程,解决与性质相关的综合性问题;
2.掌握直线与双曲线的位置关系及弦长公式. 泪水和汗水的化学成分相似,但前者只能为你换来同情,后者却可以为你赢得成功.
轴和
原点
都对
称性质双曲线范围对称
性 顶点 渐近
线离心
率图象xyxy1.了解双曲线的几何性质,并会应用于实际问
题之中.(重点)
2.会利用双曲线的定义、标准方程、几何性质
及图形四者之间的内在联系,分析和解决实
际问题.(重点、难点)探究点1 由双曲线的性质求双曲线方程已知双曲线的几何性质,求其标准方程的方法步骤:
(1)确定焦点所在的位置,以确定双曲线方程的形式;
(2)确立关于a,b,c的方程(组),求出参数a,b,c;
(3)写出标准方程.【提升总结】解:【例2】点M(x,y)与定点F(5,0)的距离和它到定
直线 的距离的比是常数 ,求点M的轨迹.xy..FOM.双曲线中应注意的几个问题:
(1)双曲线是两支曲线,而椭圆是一条封闭的曲线;
(2)双曲线的两条渐近线是区别于其他圆锥曲线所特有的;
(3)双曲线只有两个顶点,离心率e>1;
(5)注意双曲线中a,b,c,e的等量关系与椭圆中a,b,c,e的不同.【提升总结】种类: 相离; 相切; 相交(一个交点, 两个交点)探究点2 直线与双曲线的位置关系1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与双曲线的方程,
消元得到一元二次方程(当二次项系数不为0时)
(1)△>0?直线与双曲线相交?有两个公共点;
(2)△=0 ?直线与双曲线相切?有且只有一个
公共点;
(3)△<0 ?直线与双曲线相离?无公共点.通法【提升总结】直线与双曲线的位置关系:解:由双曲线的方程得,两焦点分别为F1(-3,0),F2(3,0). 因为直线AB的倾斜角是30°,且直线经过右焦点F2,所以,直线AB的方程为【提升总结】这里我们也可以利用弦长公式求解.弦长公式:或算一算,看结果一样吗?【变式练习】解析:因为F1的坐标是(-3,0),所以92.过双曲线的一个焦点F2作垂直于实轴的弦PQ,点
F1是另一个焦点,若∠PF1Q=90°,则双曲线的离
心率等于________.C4.求一条渐近线方程是3x+4y=0,一个焦点是(4,0)的双曲线标准方程.
解析:因为双曲线的一条渐近线方程为3x+4y=0,1.双曲线的简单几何性质,利用性质求方程,解决与性质相关的综合性问题;
2.掌握直线与双曲线的位置关系及弦长公式. 泪水和汗水的化学成分相似,但前者只能为你换来同情,后者却可以为你赢得成功.
