四川省昭觉中学人教版高一数学必修三(课件)3.3.2均匀随机数的产生(共34张PPT)
文档属性
| 名称 | 四川省昭觉中学人教版高一数学必修三(课件)3.3.2均匀随机数的产生(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 538.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-22 00:00:00 | ||
图片预览











文档简介
课件34张PPT。3.3.2 均匀随机数的产生 复习1、几何概型的含义是什么?它有哪两个基本特点?含义:每个事件发生的概率只与构成该事件区域的的长度(面积或体积)成比例的概率模型.特点:(1)可能出现的结果有无限多个;
(2)每个结果发生的可能性相等.2、在几何概型中,事件A的概率的计算公式: 我们常用的是[0,1]上的均匀随机数,可以利用计算器来产生.如何利用计算器产生0~1之间的均匀随机数(实数)?注意:每次结果会有不同. (2)选定Al格,点击复制,然后选定要产生随机数的格,比如A2~A100,点击粘贴,则在A1~A100的数都是[0,1]上的均匀随机数.这样我们就很快就得到了100个0~1之间的均匀随机数,相当于做了100次随机试验. (1)选定Al格,键人“=RAND()”,按Enter键,则在此格中的数是随机产生的[0,1]上的均匀随机数;用Excel演示. 试验的结果是区间[0,1]上的任何一个实数,而且出现任何一个实数是等可能的,因此,就可以用上面的方法产生的0~1之间的均匀随机数进行随机模拟. 我们可以利用计算器或计算机产生整数值随机数,还可以通过随机模拟方法求古典概型的概率近似值,对于几何概型,我们也可以进行上述工作. 思考:计算机只能产生[0,1]上的均匀随机数,如果试验的结果是区间[a,b]上等可能出现的任何一个值,如何产生[a,b]上的均匀随机数? 首先利用计算器或计算机产生[0,1]上的均匀随机数X=RAND, 然后利用伸缩和平移变换:
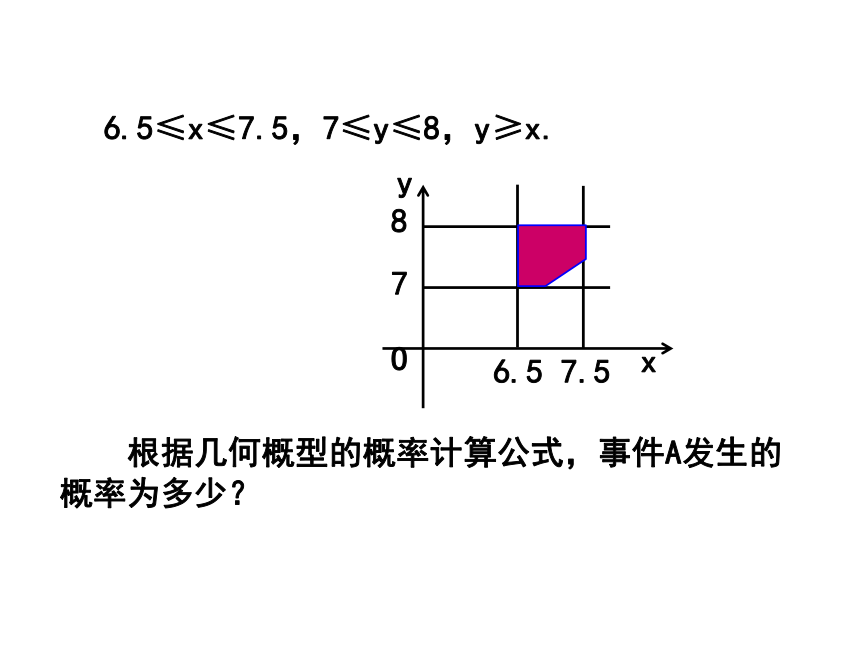
计算Y的值,则Y为[a,b]上的均匀随机数. 练习:怎样利用计算机产生100个[2,5]上的均匀随机数? (1)在A1~A100产生100个0~1之间的均匀随机数; (2)选定Bl格,键人“=A1*3+2”,按Enter键,则在此格中的数是随机产生的[2,5]上的均匀随机数; (3)选定Bl格,拖动至B100,则在B1~B100的数都是[2,5]上的均匀随机数. 例1:假设你家订了一份报纸,送报人可能在早上6:30~7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00~8:00之间,问你父亲在离开家前能得到报纸的概率是多少?随机事件 1、如果把“父亲在离开家之前能得到报纸”称为事件A,那么事件A是哪种类型的事件?分析: 2、我们有两种方法计算该事件的概率:⑴利用几何概型的公式;⑵用随机模拟的方法. 例1:假设你家订了一份报纸,送报人可能在早上6:30~7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00~8:00之间,问你父亲在离开家前能得到报纸的概率是多少?⑴利用几何概型的公式; 设送报人到达你家的时间为x,父亲离开家的时间为y,若事件A发生,则x、y应满足什么关系? 6.5≤x≤7.5,7≤y≤8,y≥x. 你能画出上述不等式组表示的平面区域吗? 根据几何概型的概率计算公式,事件A发生的概率为多少? 6.5≤x≤7.5,7≤y≤8,y≥x. 6.5≤x≤7.5,7≤y≤8,y≥x. 试验的全部结果所构成的区域为
?={(x,y)| 6.5≤x≤7.5,7≤y≤8 },这是一个正方形区域,面积为1. 6.5≤x≤7.5,7≤y≤8,y≥x. 事件A表示父亲在离开家前能得到报纸,所构成的区域A={(x,y)| 6.5≤x≤7.5,7≤y≤8, y≥x },
即图中的阴影部分,面积为这是一个几何概型,所以 思考:你能设计一种随机模拟的方法,近似计算上面事件A发生的概率吗? 例1:假设你家订了一份报纸,送报人可能在早上6:30~7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00~8:00之间,问你父亲在离开家前能得到报纸的概率是多少?⑵用随机模拟的方法. 设X、Y为[0,1]上的均匀随机数,6.5+X表示送报人到达你家的时间,7+Y表示父亲离开家的时间,若父亲在离开家之前能得到报纸,则X、Y应满足: 7+Y >6.5+X,即Y>X-0.5. (2)选定D1格,键入“=A1-B1”,按Enter键. 再选定Dl格,拖动至D50,则在D1~D50的数为Y-X的值; (3)选定E1格,键入
“=FREQUENCY(D1:D50,-0.5)”,
统计D列中小于-0.5的数的频数; 利用计算机做50次模拟试验,计算事件A发生的频率,从而估计事件A发生的概率. (1)在A1~A50,B1~B50产生两组[0,1]上的均匀随机数; 例2:在下图的正方形中随机撒一把豆子,
如何用随机模拟的方法估计
圆周率的值.(1)圆面积︰正方形面积
≈落在圆中的豆子数︰落在正方形中的豆子数.(2)设正方形的边长为2,则
圆面积︰正方形面积=?/(2×2)= ?/4.(3)由于落在每个区域的豆子数是可以数出来的,所以 ?≈落在圆中的豆子数︰落在正方形中的豆子数×4.这样就得到了?的近似值. 例2:在下图的正方形中随机撒一把豆子,
如何用随机模拟的方法估计
圆周率的值. 另外,我们可以用计算器或计算机模拟上述过程,步骤如下:⑴产生两组0-1之间的均匀随机数,a1=RAND,b1=RAND;⑵经平移和伸缩变换,a=2(a1﹣0.5),
b=2(b1﹣0.5);⑶数出落在圆内x2+y2<1的点(a,b)的个数N1,计算?=4N1/N(N代表落在正方形中的点(a,b)的个数).可以发现,随着试验次数的增加,得到的?的近似值的精度会越来越高. 本例启发我们,利用几何概型,并通过随机模拟方法可以近似计算不规则图形的面积. 例3:利用随机模拟方法计算由y=1和y=x2 所围成的图形的面积. 以直线x=1,x=-1,y=0,y=1为边界作矩形,
用随机模拟方法可以得到它的面积的近似值. 例3:利用随机模拟方法计算由y=1和y=x2 所围成的图形的面积.解:⑴产生两组0-1区间的均匀随机数,a1=RAND,b=RAND;⑵进行平移和伸缩变换,a=2(a1﹣0.5);⑶数出落在阴影内的样本点数N1,用几何概型公式计算阴影部分的面积.例4:两人约定在12∶00到1∶00之间相见,并且先到者必须等迟到者40分钟方可离去,如果两人出发是各自独立的,在12∶00至1∶00各时刻相见的可能性是相等的,求两人在约定时间内相见的概率.
两人不论谁先到都要等迟到者40分钟,即 小时,设两人分别于x时和y时到达约见地点,要使两人在约定时间范围内相见,当且仅当— ≤x—y≤ ,因此转化成面积问题,利用几何概型求解.【解】 设两人分别于x时和y时到达约见地点,要使两人能在约定时间范围内相见,
当且仅当
两人到达约见地点所有时刻(x,y)的各种可能结果可用图中的单位正方形内(包括边界)的点来表示,两人能在约定的时间范围内相见的所有时刻(x,y)的各种可能结果可用图中的阴影部分(包括边界)来表示.
因此阴影部分与单位正方形的面积比就反映了两人在约定时间范围内相遇的可能性的大小,因此所求的概率为
例5:甲、乙两人约定上午7∶00至8∶00之间到某站乘公共汽
车,在这段时间内有3班公共汽车,它们开车时刻分别为
7∶20,7∶40,8∶00,如果他们约定,见车就乘,求甲、
乙同乘一车的概率.
解:设甲到达汽车站的时刻为x,乙到达
汽车站的时刻为y,则7≤x≤8,7≤y≤8,即
甲乙两人到达汽车站的时刻(x,y)所对
应的区域在平面直角坐标系中画出(如图所示)是大正方形.将三班车到站的时刻在图形中画出,则甲乙两人要想同乘一班车,必须满足即(x,y)必须落在图形中的三个带阴影的小正方形内,
所以由几何概型的计算公式得,P=
即甲、乙同乘一车的概率为练习:甲乙两人约定在6时到7时之间在某处会面,并约定先到者应等候另一个人一刻钟,到时即可离去,求两人能会面的概率.小结 1、利用计算机和线性变换Y=X× (b-a)+a,可以产生任意区间[a,b]上的均匀随机数. 2、利用几何概型的概率公式,结合随机模拟试验,可以解决求概率、面积、参数值等一系列问题,体现了数学知识的应用价值. 3、均匀随机数在日常生活中,有着广泛的应用,我们可以利用计算器或计算机来产生均匀随机数,从而来模拟随机试验,其具体方法是:建立一个概率模型,它与某些我们感兴趣的量(如概率值、常数)有关,然后设计适当的试验,并通过这个试验的结果来确定这些量 .
(2)每个结果发生的可能性相等.2、在几何概型中,事件A的概率的计算公式: 我们常用的是[0,1]上的均匀随机数,可以利用计算器来产生.如何利用计算器产生0~1之间的均匀随机数(实数)?注意:每次结果会有不同. (2)选定Al格,点击复制,然后选定要产生随机数的格,比如A2~A100,点击粘贴,则在A1~A100的数都是[0,1]上的均匀随机数.这样我们就很快就得到了100个0~1之间的均匀随机数,相当于做了100次随机试验. (1)选定Al格,键人“=RAND()”,按Enter键,则在此格中的数是随机产生的[0,1]上的均匀随机数;用Excel演示. 试验的结果是区间[0,1]上的任何一个实数,而且出现任何一个实数是等可能的,因此,就可以用上面的方法产生的0~1之间的均匀随机数进行随机模拟. 我们可以利用计算器或计算机产生整数值随机数,还可以通过随机模拟方法求古典概型的概率近似值,对于几何概型,我们也可以进行上述工作. 思考:计算机只能产生[0,1]上的均匀随机数,如果试验的结果是区间[a,b]上等可能出现的任何一个值,如何产生[a,b]上的均匀随机数? 首先利用计算器或计算机产生[0,1]上的均匀随机数X=RAND, 然后利用伸缩和平移变换:
计算Y的值,则Y为[a,b]上的均匀随机数. 练习:怎样利用计算机产生100个[2,5]上的均匀随机数? (1)在A1~A100产生100个0~1之间的均匀随机数; (2)选定Bl格,键人“=A1*3+2”,按Enter键,则在此格中的数是随机产生的[2,5]上的均匀随机数; (3)选定Bl格,拖动至B100,则在B1~B100的数都是[2,5]上的均匀随机数. 例1:假设你家订了一份报纸,送报人可能在早上6:30~7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00~8:00之间,问你父亲在离开家前能得到报纸的概率是多少?随机事件 1、如果把“父亲在离开家之前能得到报纸”称为事件A,那么事件A是哪种类型的事件?分析: 2、我们有两种方法计算该事件的概率:⑴利用几何概型的公式;⑵用随机模拟的方法. 例1:假设你家订了一份报纸,送报人可能在早上6:30~7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00~8:00之间,问你父亲在离开家前能得到报纸的概率是多少?⑴利用几何概型的公式; 设送报人到达你家的时间为x,父亲离开家的时间为y,若事件A发生,则x、y应满足什么关系? 6.5≤x≤7.5,7≤y≤8,y≥x. 你能画出上述不等式组表示的平面区域吗? 根据几何概型的概率计算公式,事件A发生的概率为多少? 6.5≤x≤7.5,7≤y≤8,y≥x. 6.5≤x≤7.5,7≤y≤8,y≥x. 试验的全部结果所构成的区域为
?={(x,y)| 6.5≤x≤7.5,7≤y≤8 },这是一个正方形区域,面积为1. 6.5≤x≤7.5,7≤y≤8,y≥x. 事件A表示父亲在离开家前能得到报纸,所构成的区域A={(x,y)| 6.5≤x≤7.5,7≤y≤8, y≥x },
即图中的阴影部分,面积为这是一个几何概型,所以 思考:你能设计一种随机模拟的方法,近似计算上面事件A发生的概率吗? 例1:假设你家订了一份报纸,送报人可能在早上6:30~7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00~8:00之间,问你父亲在离开家前能得到报纸的概率是多少?⑵用随机模拟的方法. 设X、Y为[0,1]上的均匀随机数,6.5+X表示送报人到达你家的时间,7+Y表示父亲离开家的时间,若父亲在离开家之前能得到报纸,则X、Y应满足: 7+Y >6.5+X,即Y>X-0.5. (2)选定D1格,键入“=A1-B1”,按Enter键. 再选定Dl格,拖动至D50,则在D1~D50的数为Y-X的值; (3)选定E1格,键入
“=FREQUENCY(D1:D50,-0.5)”,
统计D列中小于-0.5的数的频数; 利用计算机做50次模拟试验,计算事件A发生的频率,从而估计事件A发生的概率. (1)在A1~A50,B1~B50产生两组[0,1]上的均匀随机数; 例2:在下图的正方形中随机撒一把豆子,
如何用随机模拟的方法估计
圆周率的值.(1)圆面积︰正方形面积
≈落在圆中的豆子数︰落在正方形中的豆子数.(2)设正方形的边长为2,则
圆面积︰正方形面积=?/(2×2)= ?/4.(3)由于落在每个区域的豆子数是可以数出来的,所以 ?≈落在圆中的豆子数︰落在正方形中的豆子数×4.这样就得到了?的近似值. 例2:在下图的正方形中随机撒一把豆子,
如何用随机模拟的方法估计
圆周率的值. 另外,我们可以用计算器或计算机模拟上述过程,步骤如下:⑴产生两组0-1之间的均匀随机数,a1=RAND,b1=RAND;⑵经平移和伸缩变换,a=2(a1﹣0.5),
b=2(b1﹣0.5);⑶数出落在圆内x2+y2<1的点(a,b)的个数N1,计算?=4N1/N(N代表落在正方形中的点(a,b)的个数).可以发现,随着试验次数的增加,得到的?的近似值的精度会越来越高. 本例启发我们,利用几何概型,并通过随机模拟方法可以近似计算不规则图形的面积. 例3:利用随机模拟方法计算由y=1和y=x2 所围成的图形的面积. 以直线x=1,x=-1,y=0,y=1为边界作矩形,
用随机模拟方法可以得到它的面积的近似值. 例3:利用随机模拟方法计算由y=1和y=x2 所围成的图形的面积.解:⑴产生两组0-1区间的均匀随机数,a1=RAND,b=RAND;⑵进行平移和伸缩变换,a=2(a1﹣0.5);⑶数出落在阴影内的样本点数N1,用几何概型公式计算阴影部分的面积.例4:两人约定在12∶00到1∶00之间相见,并且先到者必须等迟到者40分钟方可离去,如果两人出发是各自独立的,在12∶00至1∶00各时刻相见的可能性是相等的,求两人在约定时间内相见的概率.
两人不论谁先到都要等迟到者40分钟,即 小时,设两人分别于x时和y时到达约见地点,要使两人在约定时间范围内相见,当且仅当— ≤x—y≤ ,因此转化成面积问题,利用几何概型求解.【解】 设两人分别于x时和y时到达约见地点,要使两人能在约定时间范围内相见,
当且仅当
两人到达约见地点所有时刻(x,y)的各种可能结果可用图中的单位正方形内(包括边界)的点来表示,两人能在约定的时间范围内相见的所有时刻(x,y)的各种可能结果可用图中的阴影部分(包括边界)来表示.
因此阴影部分与单位正方形的面积比就反映了两人在约定时间范围内相遇的可能性的大小,因此所求的概率为
例5:甲、乙两人约定上午7∶00至8∶00之间到某站乘公共汽
车,在这段时间内有3班公共汽车,它们开车时刻分别为
7∶20,7∶40,8∶00,如果他们约定,见车就乘,求甲、
乙同乘一车的概率.
解:设甲到达汽车站的时刻为x,乙到达
汽车站的时刻为y,则7≤x≤8,7≤y≤8,即
甲乙两人到达汽车站的时刻(x,y)所对
应的区域在平面直角坐标系中画出(如图所示)是大正方形.将三班车到站的时刻在图形中画出,则甲乙两人要想同乘一班车,必须满足即(x,y)必须落在图形中的三个带阴影的小正方形内,
所以由几何概型的计算公式得,P=
即甲、乙同乘一车的概率为练习:甲乙两人约定在6时到7时之间在某处会面,并约定先到者应等候另一个人一刻钟,到时即可离去,求两人能会面的概率.小结 1、利用计算机和线性变换Y=X× (b-a)+a,可以产生任意区间[a,b]上的均匀随机数. 2、利用几何概型的概率公式,结合随机模拟试验,可以解决求概率、面积、参数值等一系列问题,体现了数学知识的应用价值. 3、均匀随机数在日常生活中,有着广泛的应用,我们可以利用计算器或计算机来产生均匀随机数,从而来模拟随机试验,其具体方法是:建立一个概率模型,它与某些我们感兴趣的量(如概率值、常数)有关,然后设计适当的试验,并通过这个试验的结果来确定这些量 .
