2025年中考数学一模猜题卷(安徽省专用)—2025年全国各地市最新中考数学模拟考试(含答案)
文档属性
| 名称 | 2025年中考数学一模猜题卷(安徽省专用)—2025年全国各地市最新中考数学模拟考试(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 20:48:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
机密★启用前
2025 年 安 徽 省 中 考 一 模 猜 题 卷
数 学
注意事项:
I.你拿到的试卷满分为150 分, 考试时间为120 分钟。
2.本试卷包括“ 试题卷" 和“ 答题" 两部分。“ 试卷“ 共4 页答题卷“ 共6 页。
3.请务必在“ 答题卷" 上答题, 在“ 试卷" 上答題是无效的。
4.考试结束后, 将“ 试地卷" 和“ 答卷" 一并交回。
一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
1.下列各组数中,数值相等的是( )
A.和 B.和
C.和 D.和
2. 2024 年浙江经济第一季度 GDP为201370000万元,其中201370000用科学记数法表示为 ( )
A. B.
C. D.
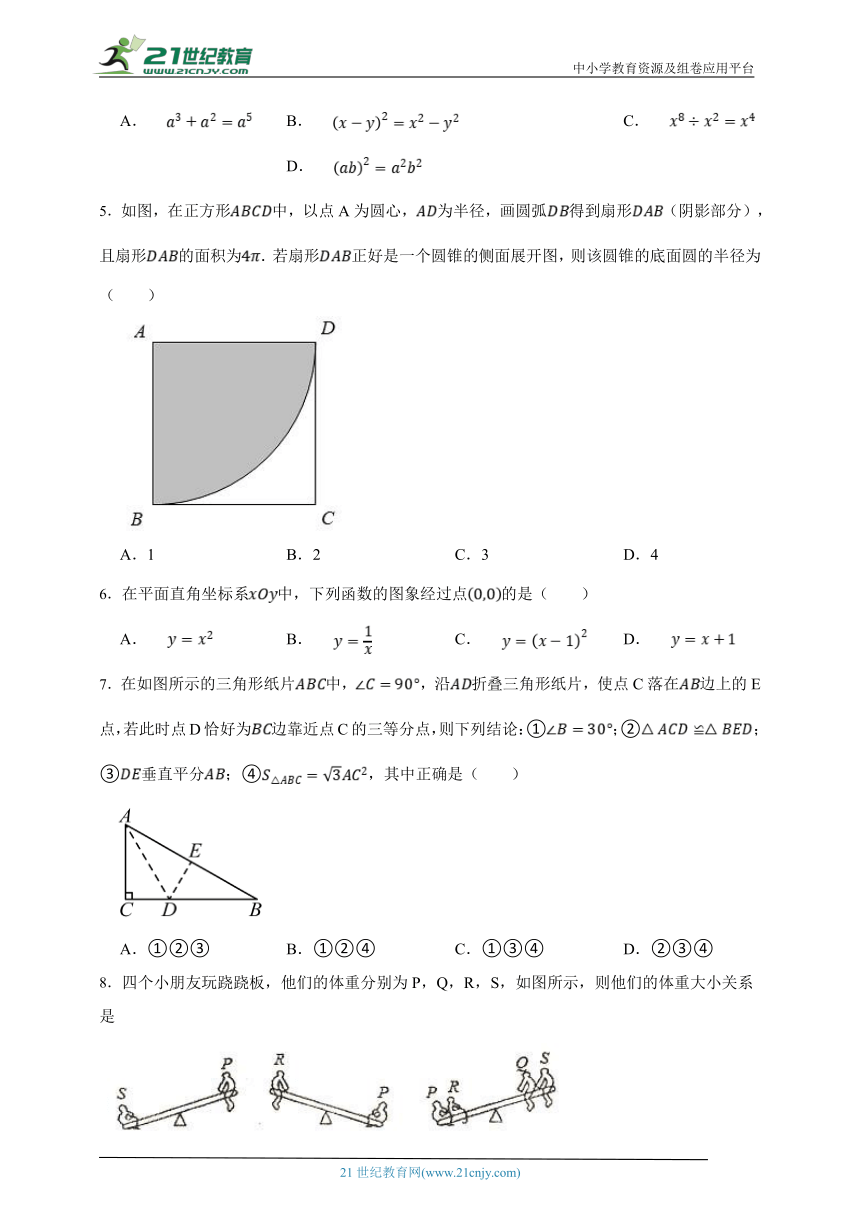
3.如图,这是一个由两个等高的几何体组成的图形的三视图,则这个组合图形摆放正确的是( )
A. B.
C. D.
4.下列运算,其中正确的是( )
A. B. C. D.
5.如图,在正方形中,以点A为圆心,为半径,画圆弧得到扇形(阴影部分),且扇形的面积为.若扇形正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径为( )
A.1 B.2 C.3 D.4
6.在平面直角坐标系中,下列函数的图象经过点的是( )
A. B. C. D.
7.在如图所示的三角形纸片中,,沿折叠三角形纸片,使点C落在边上的E点,若此时点D恰好为边靠近点C的三等分点,则下列结论:①;②;③垂直平分;④,其中正确是( )
A.①②③ B.①②④ C.①③④ D.②③④
8.四个小朋友玩跷跷板,他们的体重分别为P,Q,R,S,如图所示,则他们的体重大小关系是
A.P>R>S>Q B.Q>S>P>R C.S>P>Q>R D.S>P>R>Q
9.如图,在、上各取一点E、D,使,连接、相交于点O,再连接、,若,则图中全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
10.把两个全等的等腰直角三角形透明纸片如图1放置(点与点重合),若将绕点在平面内旋转,分别交边于点(点均不与点重合).设,在旋转过程中,与的函数关系图象如图2所示,则下列结论中正确的是( )
A. B.
C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若分式有意义,则x满足的条件 .
12. 写出一个比 大的整数, 可以是 .
13.扬州市义务教育学业质量监测实施方案如下:3、4、5年级在语文、数学、英语3个科目中各抽1个科目进行测试,各年级测试科目不同,对于4年级学生,抽到数学科目的概率为
14.如图,在正方形ABCD的对角线AC上取一点E,使得,连接BE,将沿BE翻折得到,连接DF.若,则DF的长为 .
三、(本大题共2小题,每小题8分,满分16分)
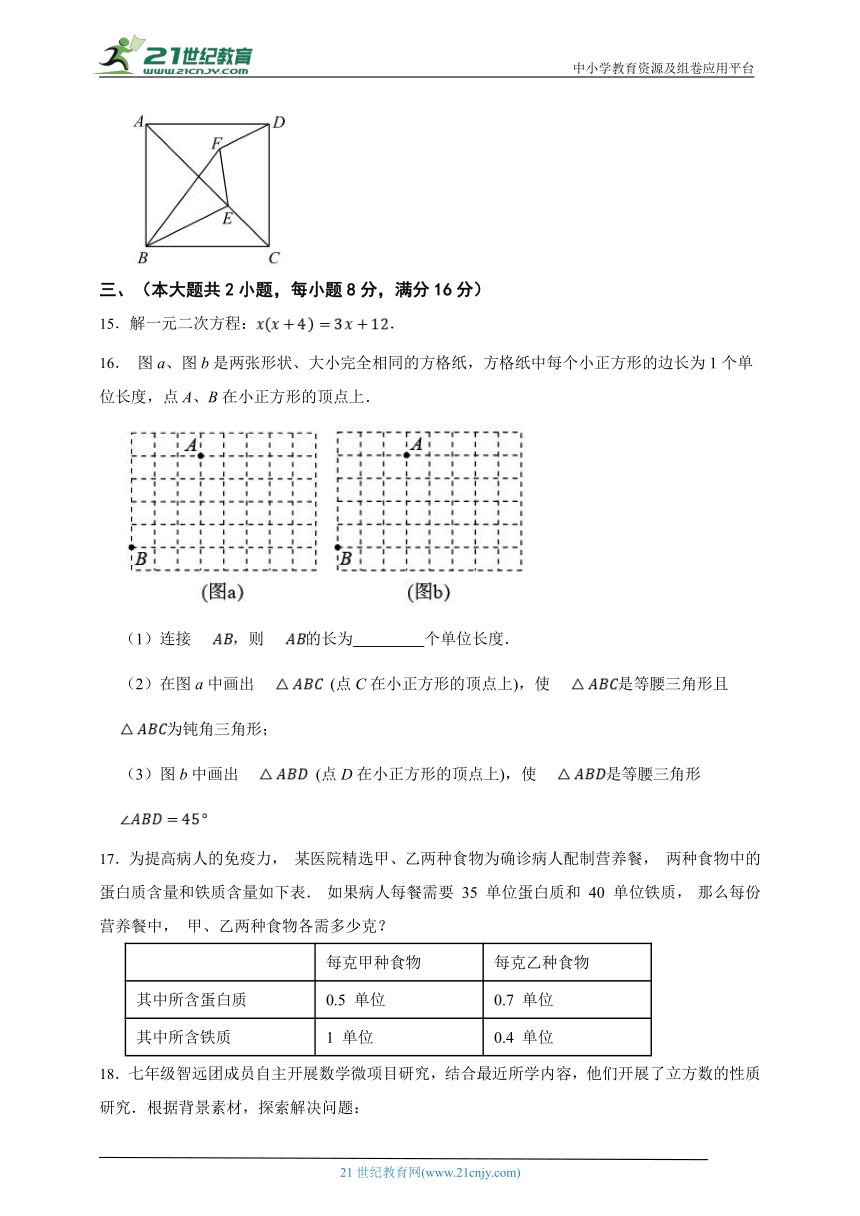
15.解一元二次方程:.
16. 图a、图b是两张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长为1个单位长度,点A、B在小正方形的顶点上.
(1)连接,则的长为 个单位长度.
(2)在图a中画出 (点C在小正方形的顶点上),使是等腰三角形且为钝角三角形;
(3)图b中画出 (点D在小正方形的顶点上),使是等腰三角形
17.为提高病人的免疫力, 某医院精选甲、乙两种食物为确诊病人配制营养餐, 两种食物中的蛋白质含量和铁质含量如下表. 如果病人每餐需要 35 单位蛋白质和 40 单位铁质, 那么每份营养餐中, 甲、乙两种食物各需多少克?
每克甲种食物 每克乙种食物
其中所含蛋白质 0.5 单位 0.7 单位
其中所含铁质 1 单位 0.4 单位
18.七年级智远团成员自主开展数学微项目研究,结合最近所学内容,他们开展了立方数的性质研究.根据背景素材,探索解决问题:
探索立方数的性质
素材 古希腊数学家发现:一个正整数k的三次幂总能表示成k个连续奇数之和. 举例论证:13=123=3+533=7+9+11①请按规律写出:43= ▲ .
归纳数学规律 ②如果k3表示成k个连续奇数之和时,其中有一个奇数是35,k= ▲ ③当k=10时,等号右边的式子的中间两个数(即第5个数和第6个数)是 ▲ .
应用数学规律 ④利用这个结论计算:13+23+33+…+103+113
四、(本大题共2小题,每小题10分,满分20分)
19.如图,为了测量河对岸两点A,B之间的距离,在河岸这边取点C,D.测得,,,,,设A,B,C,D在同一平面内,求A,B两点之间的距离.(参考数据:.)
20.如图,在中,,,.O为边上一点,以O为圆心,为半径作半圆,分别于与边交于点D、E,连接.
(1) °;
(2)当时,求的长;
(3)过点E作半圆O的切线,当切线与边相交时,设交点为F.求证:.
五、(本题满分12分)
21. 综合与实践
【问题情境】数学活动课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动.
【实践发现】同学们随机收集芒果树、荔枝树的树叶各 10 片,通过测量得到这些树叶的长 (单位: ), 宽 (单位: )的数据后, 分别计算长宽比, 整理数据如下.
1 2 3 4 5 6 7 8 9 10
芒果树叶的长宽比 3.8 3.7 3.5 3.4 3.8 4.0 3.6 4.0 3.6 4.0
荔枝树叶的长宽比 2.0 2.0 2.0 2.4 1.8 1.9 1.8 2.0 1.3 1.9
【实践探究】分析数据如下.
平均数 中位数 众数 方差
芒果树叶的长宽比 3.74 4.0 0.0424
荔枝树叶的长宽比 1.91 1.95 0.0669
【问题解决】
(1)上述表格中: ,
(2) ① 同学说: “从树叶的长宽比的方差来看, 我认为芒果树叶的形状差别大.”
② 同学说:“从树叶的长宽比的平均数、中位数和众数来看, 我发现荔枝树叶的长约为宽的两倍. ”
上面两名同学的说法中,合理的是 (填序号).
(3) 现有一片长 11 , 宽 的树叶, 请判断这片树叶更可能来自芒果、荔枝中的哪种树?并给出你的理由.
22.如图①,在正方形中,点,分别在,边上,,,垂足为,过点作,交于点.
(1)求证:;
(2)求的值(用含的代数式表示);
(3)如图②,当时,连接并延长,交于点,求证:.
六、(本题满分14分)
23.在平面直角坐标系中,抛物线与轴交于点,将点向右平移个单位长度,得到点.
(1)若,点在抛物线上,求抛物线的解析式及对称轴;
(2)若抛物线与线段恰有一个公共点,结合函数图象,求的取值范围.
答案解析部分
1.D
2.D
3.B
4.D
5.A
6.A
7.A
8.D
9.D
10.D
11.
12.2(答案不唯一)
13.
14.
15.,
16.(1)5
(2)解:如图,即为所求,
;
(3)解:如图,即为所求,
.
17.解:设甲、乙两种食物各需 克, 克,则
答: 每份营养餐中,甲、乙两种食物各需 28 克, 30 克.
18.解:①13+15+17+19;
②6;
③99,101;
④13+23+33+…+93+103+113
=1+(3+5)+(7+9+11)+……+(111+113+115+117+119+121+123+125+127+129+131)
=×66×(1+131)
=4356;
19.52m
20.(1)90
(2)解:∵,,,
在中,根据勾股定理,得.
∵为直径,
∴,
∴.
又∵,
∴.
∴,
即,
∴;
(3)证明:连接,
∵为半圆O的切线,
∴,
∴,
∵,
∴,
∵,
∴,
又∵,
∴,
∴,
∴.
21.(1)3.75;2.0
(2)②
(3)解:∵11÷5.6≈1.96≈2,
∴这片树叶更可能是荔枝树叶.
22.(1)证明:∵,
∴,
∴.
∵在正方形中,,,
∴,
∴,
∴,
∴;
(2)解:延长交于点,
在正方形中,,,
又∵,
∴四边形是平行四边形,,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴;
(3)证明:
∵,,
∴,
设正方形的边长为,则,
∴在中,由勾股定理得,
∵在正方形中,,
∴,
∵,
∴,
∵,
∴,
∴,,
∴,,
∴,
∴,
∴,
∴,
∵在正方形中,,
∴,,
∴,
∴,
∴,
∴,
∴,
∴.
23.(1)解:若,则抛物线为,
点在抛物线上,
,
,
抛物线为,
抛物线的对称轴为直线;
(2)解:当时,如图.
抛物线的对称轴为直线,
将点向右平移个单位长度,得到点,抛物线与线段恰有一个公共点,
,
;
当时,如图.
抛物线的对称轴为直线,
抛物线与线段只有一个公共点,
,
综上所述,的取值范围是:或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
机密★启用前
2025 年 安 徽 省 中 考 一 模 猜 题 卷
数 学
注意事项:
I.你拿到的试卷满分为150 分, 考试时间为120 分钟。
2.本试卷包括“ 试题卷" 和“ 答题" 两部分。“ 试卷“ 共4 页答题卷“ 共6 页。
3.请务必在“ 答题卷" 上答题, 在“ 试卷" 上答題是无效的。
4.考试结束后, 将“ 试地卷" 和“ 答卷" 一并交回。
一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
1.下列各组数中,数值相等的是( )
A.和 B.和
C.和 D.和
2. 2024 年浙江经济第一季度 GDP为201370000万元,其中201370000用科学记数法表示为 ( )
A. B.
C. D.
3.如图,这是一个由两个等高的几何体组成的图形的三视图,则这个组合图形摆放正确的是( )
A. B.
C. D.
4.下列运算,其中正确的是( )
A. B. C. D.
5.如图,在正方形中,以点A为圆心,为半径,画圆弧得到扇形(阴影部分),且扇形的面积为.若扇形正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径为( )
A.1 B.2 C.3 D.4
6.在平面直角坐标系中,下列函数的图象经过点的是( )
A. B. C. D.
7.在如图所示的三角形纸片中,,沿折叠三角形纸片,使点C落在边上的E点,若此时点D恰好为边靠近点C的三等分点,则下列结论:①;②;③垂直平分;④,其中正确是( )
A.①②③ B.①②④ C.①③④ D.②③④
8.四个小朋友玩跷跷板,他们的体重分别为P,Q,R,S,如图所示,则他们的体重大小关系是
A.P>R>S>Q B.Q>S>P>R C.S>P>Q>R D.S>P>R>Q
9.如图,在、上各取一点E、D,使,连接、相交于点O,再连接、,若,则图中全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
10.把两个全等的等腰直角三角形透明纸片如图1放置(点与点重合),若将绕点在平面内旋转,分别交边于点(点均不与点重合).设,在旋转过程中,与的函数关系图象如图2所示,则下列结论中正确的是( )
A. B.
C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若分式有意义,则x满足的条件 .
12. 写出一个比 大的整数, 可以是 .
13.扬州市义务教育学业质量监测实施方案如下:3、4、5年级在语文、数学、英语3个科目中各抽1个科目进行测试,各年级测试科目不同,对于4年级学生,抽到数学科目的概率为
14.如图,在正方形ABCD的对角线AC上取一点E,使得,连接BE,将沿BE翻折得到,连接DF.若,则DF的长为 .
三、(本大题共2小题,每小题8分,满分16分)
15.解一元二次方程:.
16. 图a、图b是两张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长为1个单位长度,点A、B在小正方形的顶点上.
(1)连接,则的长为 个单位长度.
(2)在图a中画出 (点C在小正方形的顶点上),使是等腰三角形且为钝角三角形;
(3)图b中画出 (点D在小正方形的顶点上),使是等腰三角形
17.为提高病人的免疫力, 某医院精选甲、乙两种食物为确诊病人配制营养餐, 两种食物中的蛋白质含量和铁质含量如下表. 如果病人每餐需要 35 单位蛋白质和 40 单位铁质, 那么每份营养餐中, 甲、乙两种食物各需多少克?
每克甲种食物 每克乙种食物
其中所含蛋白质 0.5 单位 0.7 单位
其中所含铁质 1 单位 0.4 单位
18.七年级智远团成员自主开展数学微项目研究,结合最近所学内容,他们开展了立方数的性质研究.根据背景素材,探索解决问题:
探索立方数的性质
素材 古希腊数学家发现:一个正整数k的三次幂总能表示成k个连续奇数之和. 举例论证:13=123=3+533=7+9+11①请按规律写出:43= ▲ .
归纳数学规律 ②如果k3表示成k个连续奇数之和时,其中有一个奇数是35,k= ▲ ③当k=10时,等号右边的式子的中间两个数(即第5个数和第6个数)是 ▲ .
应用数学规律 ④利用这个结论计算:13+23+33+…+103+113
四、(本大题共2小题,每小题10分,满分20分)
19.如图,为了测量河对岸两点A,B之间的距离,在河岸这边取点C,D.测得,,,,,设A,B,C,D在同一平面内,求A,B两点之间的距离.(参考数据:.)
20.如图,在中,,,.O为边上一点,以O为圆心,为半径作半圆,分别于与边交于点D、E,连接.
(1) °;
(2)当时,求的长;
(3)过点E作半圆O的切线,当切线与边相交时,设交点为F.求证:.
五、(本题满分12分)
21. 综合与实践
【问题情境】数学活动课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动.
【实践发现】同学们随机收集芒果树、荔枝树的树叶各 10 片,通过测量得到这些树叶的长 (单位: ), 宽 (单位: )的数据后, 分别计算长宽比, 整理数据如下.
1 2 3 4 5 6 7 8 9 10
芒果树叶的长宽比 3.8 3.7 3.5 3.4 3.8 4.0 3.6 4.0 3.6 4.0
荔枝树叶的长宽比 2.0 2.0 2.0 2.4 1.8 1.9 1.8 2.0 1.3 1.9
【实践探究】分析数据如下.
平均数 中位数 众数 方差
芒果树叶的长宽比 3.74 4.0 0.0424
荔枝树叶的长宽比 1.91 1.95 0.0669
【问题解决】
(1)上述表格中: ,
(2) ① 同学说: “从树叶的长宽比的方差来看, 我认为芒果树叶的形状差别大.”
② 同学说:“从树叶的长宽比的平均数、中位数和众数来看, 我发现荔枝树叶的长约为宽的两倍. ”
上面两名同学的说法中,合理的是 (填序号).
(3) 现有一片长 11 , 宽 的树叶, 请判断这片树叶更可能来自芒果、荔枝中的哪种树?并给出你的理由.
22.如图①,在正方形中,点,分别在,边上,,,垂足为,过点作,交于点.
(1)求证:;
(2)求的值(用含的代数式表示);
(3)如图②,当时,连接并延长,交于点,求证:.
六、(本题满分14分)
23.在平面直角坐标系中,抛物线与轴交于点,将点向右平移个单位长度,得到点.
(1)若,点在抛物线上,求抛物线的解析式及对称轴;
(2)若抛物线与线段恰有一个公共点,结合函数图象,求的取值范围.
答案解析部分
1.D
2.D
3.B
4.D
5.A
6.A
7.A
8.D
9.D
10.D
11.
12.2(答案不唯一)
13.
14.
15.,
16.(1)5
(2)解:如图,即为所求,
;
(3)解:如图,即为所求,
.
17.解:设甲、乙两种食物各需 克, 克,则
答: 每份营养餐中,甲、乙两种食物各需 28 克, 30 克.
18.解:①13+15+17+19;
②6;
③99,101;
④13+23+33+…+93+103+113
=1+(3+5)+(7+9+11)+……+(111+113+115+117+119+121+123+125+127+129+131)
=×66×(1+131)
=4356;
19.52m
20.(1)90
(2)解:∵,,,
在中,根据勾股定理,得.
∵为直径,
∴,
∴.
又∵,
∴.
∴,
即,
∴;
(3)证明:连接,
∵为半圆O的切线,
∴,
∴,
∵,
∴,
∵,
∴,
又∵,
∴,
∴,
∴.
21.(1)3.75;2.0
(2)②
(3)解:∵11÷5.6≈1.96≈2,
∴这片树叶更可能是荔枝树叶.
22.(1)证明:∵,
∴,
∴.
∵在正方形中,,,
∴,
∴,
∴,
∴;
(2)解:延长交于点,
在正方形中,,,
又∵,
∴四边形是平行四边形,,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴;
(3)证明:
∵,,
∴,
设正方形的边长为,则,
∴在中,由勾股定理得,
∵在正方形中,,
∴,
∵,
∴,
∵,
∴,
∴,,
∴,,
∴,
∴,
∴,
∴,
∵在正方形中,,
∴,,
∴,
∴,
∴,
∴,
∴,
∴.
23.(1)解:若,则抛物线为,
点在抛物线上,
,
,
抛物线为,
抛物线的对称轴为直线;
(2)解:当时,如图.
抛物线的对称轴为直线,
将点向右平移个单位长度,得到点,抛物线与线段恰有一个公共点,
,
;
当时,如图.
抛物线的对称轴为直线,
抛物线与线段只有一个公共点,
,
综上所述,的取值范围是:或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
