2025年中考数学一模猜题卷(河北专用)—2025年全国各地市最新中考数学模拟考试(含答案)
文档属性
| 名称 | 2025年中考数学一模猜题卷(河北专用)—2025年全国各地市最新中考数学模拟考试(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 20:54:43 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
机密★启用前
2025 年 河 北 中 考 一 模 猜 题 卷
数 学
〈全卷满分120 分, 考试时间120 分钟)
注意事项
1.答题前, 考生务必将姓名、准考证号填写在试卷和答题卡上·
2 .考生作答时, 请在答题卡上作答〈答题注意事项见答题卡), 在本试卷、草稿纸上作答无效。
3 .不能使用计算器。
4 .考试结束后, 将本试卷和答题卡一并交回·
一、选择题(本大题共16个小题,共38分.1~6小题各3分,7~16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.1,0,,四个数中,最大的数是( )
A.1 B.0 C. D.
2.下列计算正确的是( )
A. B.
C. D.
3.下列命题中,假命题的是( )
A.面积相等的两个三角形全等
B.等腰三角形的顶角平分线垂直于底边
C.在同一平面内,垂直于同一条直线的两条直线平行
D.三角形的一个外角大于任何一个与它不相邻的内角
4.若二次根式有意义,则x的取值范围是( )
A. B. C. D.
5.要求画的边上的高.下列画法中,正确的是( )
A. B.
C. D.
6.五个大小相同的正方体搭成的几何体如图所示,其主视图是( )
A. B.
C. D.
7.小丽要把一篇文章录入电脑,如图是录入时间(分钟)与录字速度(字/分钟)成反比例函数的图象,该图象经过点.根据图象可知,下列说法不正确的是( )
A.这篇文章一共1500字.
B.当小丽的录字速度为75字/分钟时,录入时间为20分钟.
C.小丽在19:20开始录入,要求完成录入时不超过19:35,则小丽每分钟至少应录入90字.
D.小丽原计划每分钟录入125字,实际录入速度比原计划提高了,则小丽会比原计划提前2分钟完成任务.
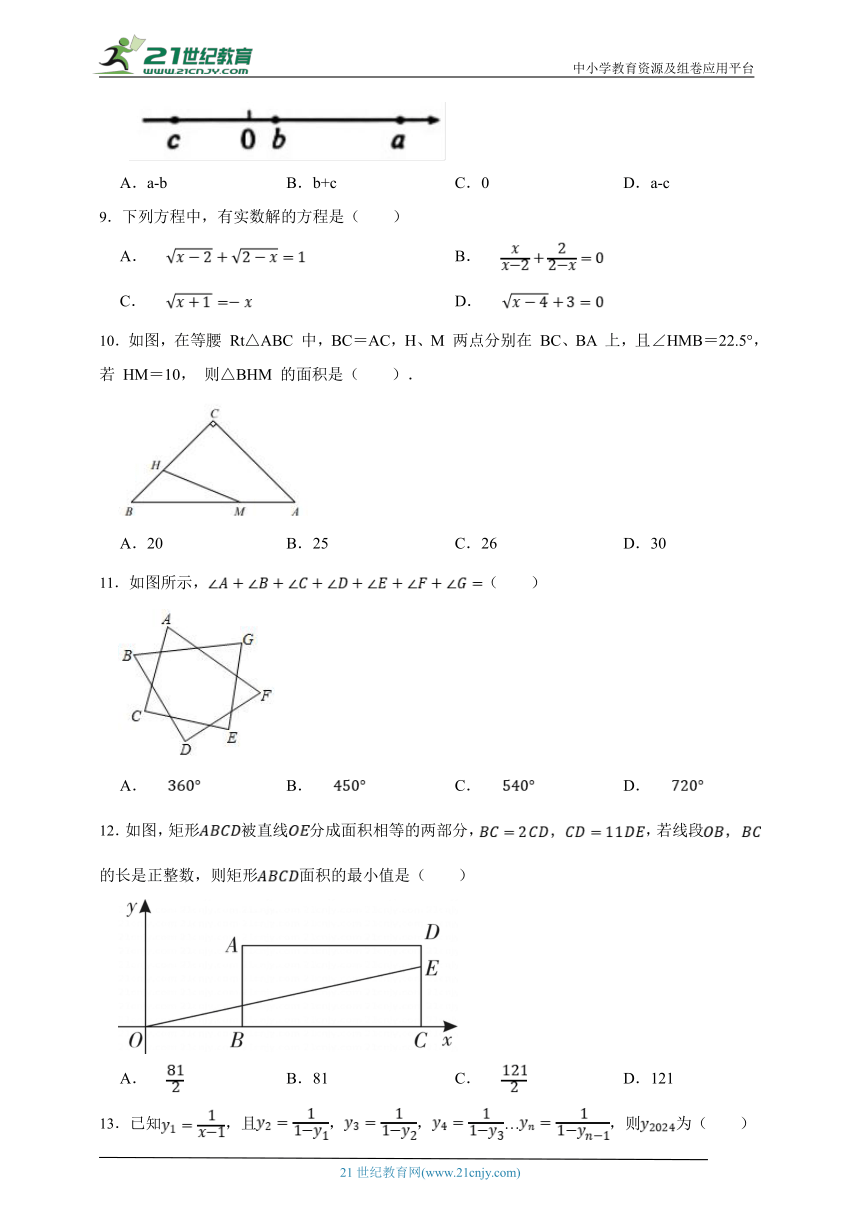
8. 已知实数a,b,c在数轴上的对应点的位置如图所示,化简|a-b|+|b-c|-|c-a|的结果是 ( )
A.a-b B.b+c C.0 D.a-c
9.下列方程中,有实数解的方程是( )
A. B.
C. D.
10.如图,在等腰 Rt△ABC 中,BC=AC,H、M 两点分别在 BC、BA 上,且∠HMB=22.5°,若 HM=10, 则△BHM 的面积是( ).
A.20 B.25 C.26 D.30
11.如图所示,( )
A. B. C. D.
12.如图,矩形被直线分成面积相等的两部分,,若线段的长是正整数,则矩形面积的最小值是( )
A. B.81 C. D.121
13.已知,且,,…,则为( )
A. B. C. D.
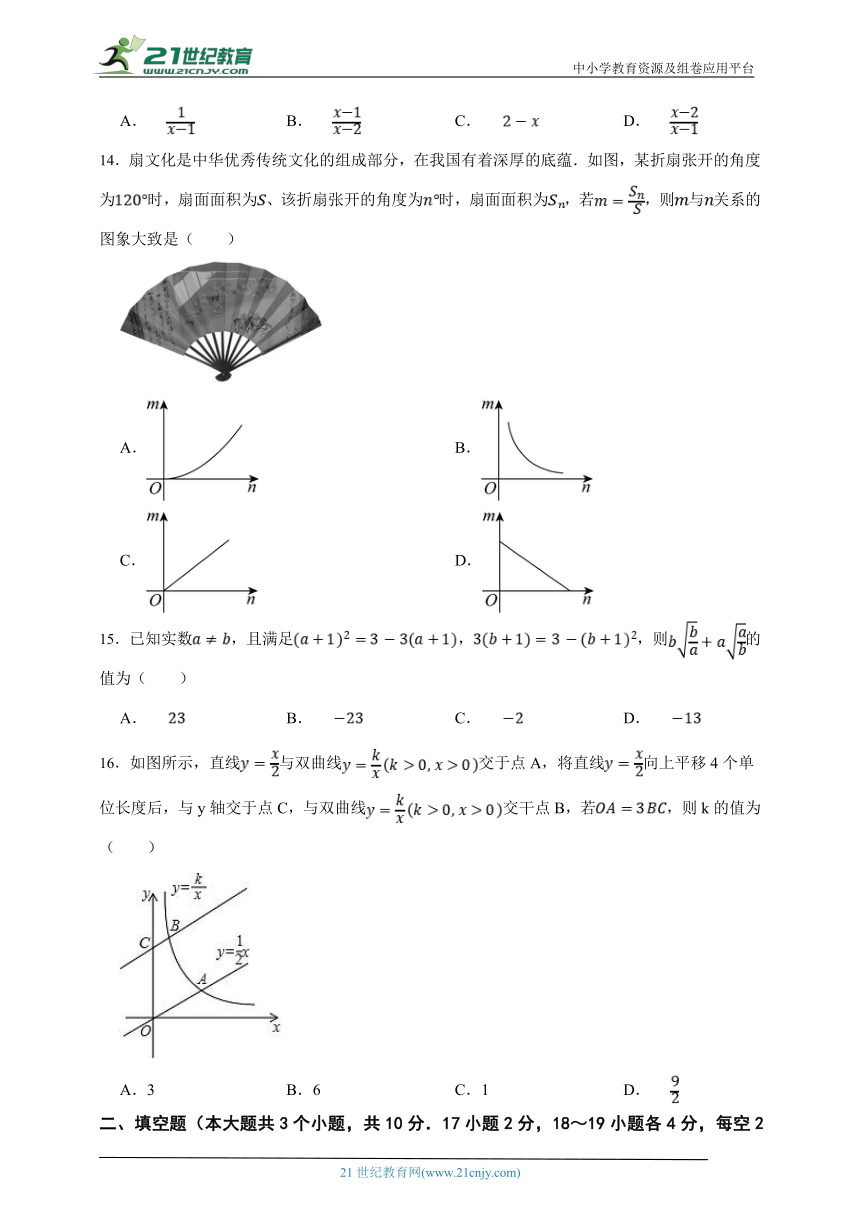
14.扇文化是中华优秀传统文化的组成部分,在我国有着深厚的底蕴.如图,某折扇张开的角度为时,扇面面积为、该折扇张开的角度为时,扇面面积为,若,则与关系的图象大致是( )
A. B.
C. D.
15.已知实数,且满足,,则的值为( )
A. B. C. D.
16.如图所示,直线与双曲线交于点A,将直线向上平移4个单位长度后,与y轴交于点C,与双曲线交干点B,若,则k的值为( )
A.3 B.6 C.1 D.
二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分)
17.“科学用眼,保护视力”是青少年珍爱生命的具体表现.某班50名同学的视力检查数据如表所示,其中有两个数据被墨汁遮盖了,以下关于视力的统计量中可以确定的是 (填写正确的序号).
视力 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 3 3 6 9 12 10
①平均数 ②众数 ③方差
18.规定用符号表示一个实数的整数部分,例如:,,按此规定的值为 .
19.勾股定理的证明方法多样.如图正方形是由小正方形和四个全等的直角三角形无缝密铺组成.延长交以为直径的圆于点(点在的上侧),连结,.分别以,为边向外作正方形,.已知的面积为2,正方形的面积为1,则正方形的面积为 .
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
20.如图,数轴上点,,对应的数分别为,,,且,将点向左移动个单位长度到达点,将点向右移动个单位长度到达点.
(1)_______,_______;
(2)若将数轴折叠,使得点与点重合,求与点重合的点表示的数.
21. 小刚和小明两位同学玩一种游戏.游戏规则为:两人各执“象、虎、鼠”三张牌,同时各出一张牌定胜负,其中象胜虎、虎胜鼠、鼠胜象,若两人所出牌相同,则为平局.例如,小刚出象牌,小明出虎牌,则小刚胜;又如,两人同时出象牌,则两人平局.
(1)一次出牌小刚出“象”牌的概率是多少.
(2)如果用A,B,C分别表示小刚的象、虎、鼠三张牌,用A1,B1,C1分别表示小明的象、虎、鼠三张牌,那么一次出牌小刚胜小明的概率是多少 用列表法或画树状图法加以说明.
(3)你认为这个游戏对小刚和小明公平吗 为什么
22.随着数字转型世界大会的召开,引领时尚,无人机走进人们生活.周末小华利用无人机来测量汶河上,两点之间的距离(,位于同一水平地面上),如图所示,小华站在处遥控空中处的无人机,此时他的仰角为,无人机的飞行高度为,并且无人机测得河岸边处的俯角为,若小华的身高,(点,,,在同一平面内).
(1)求小华的仰角的正切值;
(2)求、两点之间的距离.
23. 如图
(1)【探索发现】如图1,正方形的对角线相交于点O,点O又是正方形的一个顶点,而且这两个正方形的边长相等,我们知道,无论正方形绕点O怎么转动,总有,连接,求证:.
(2)【类比迁移】如图2,矩形的中心O是矩形的一个顶点,与边相交于点E,与边相交于点F,连接,矩形可绕着点O旋转,判断(1)中的结论是否成立,若成立,请证明,若不成立,请说明理由;
(3)【迁移拓展】如图3,在中,,,,直角的顶点D在边的中点处,它的两条边和分别与直线相交于点E,F,可绕着点D旋转,当时,直接写出线段的长度.
24.[应用意识]某包装公司承接到 21 600 个旅行包的订单,准备将任务分配给甲、乙两个车间去完成.由于他们的设备与人数不同,甲车间每天生产的总数是乙车间每天生产总数的2倍,甲车间单独完成这项工作所需的时间比乙车间单独完成少 18 天.
(1)问甲、乙车间每天分别生产多少个旅行包
(2)若已知甲车间每人每天生产 60个旅行包,乙车间每人每天生产 40个旅行包.因另有紧急任务,公司决定在甲、乙两车间抽走相等数量的工人.为了使抽走工人后甲、乙两车间每天生产的总数之和保持不变,余下的所有工人每天的生产个数需要提高 20%,求甲、乙每个车间被抽走了的人数.
25.如图,在平面直角坐标系中,点M是第一象限内一点,过M的直线分别交x轴,y轴的正半轴于A,B两点,且M是AB的中点.以OM为直径的⊙P分别交x轴,y轴于C,D两点,交直线AB于点E(位于点M右下方),连结DE交OM于点K.
(1)若点M的坐标为(3,4),
①求A,B两点的坐标;
②求ME的长.
(2)若 =3,求∠OBA的度数.
(3)设tan∠OBA=x(0<x<1), =y,直接写出y关于x的函数解析式.
26.如图,抛物线与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,点A、B的坐标为,
图1 图2
(1)如图1,求抛物线的解析式;
(2)如图1,点D在直线BC上方的抛物线上运动(不含端点B、C),连接DC、DB,当△BCD面积最大时,求出面积最大值和点D的坐标;
(3)如图2,将(1)中的抛物线向右平移,当它恰好经过原点时,设原抛物线与平移后的抛物线交于点E,连接BE.点M为原抛物线对称轴上一点,以B、E、M为顶点的三角形是直角三角形时,写出所有符合条件的点M的坐标,并写出求解点M的坐标的其中一种情况.
答案解析部分
1.A
解:由题意可得:
-12<-2<0<1
故答案为:A
直接比较大小即可求出答案.
2.D
3.A
4.B
5.C
解:A、图中为边上的高,不符合题意;
B、图中不是高,不符合题意;
C、图中为边上的高,符合题意;
D、图中为边上的高,不符合题意;
故选:C.
根据从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高,逐项分析即可求解.
6.A
7.C
8.C
解:根据题意可得:c<0∴a-b>0,b-c>0,c-a<0,
∴|a-b|+|b-c|-|c-a|=a-b+b-c-(a-c)=a-b+b-c-a+c=0,
故答案为:C.
先根据题意及数轴判断出a-b>0,b-c>0,c-a<0,再去掉绝对值,最后合并同类项即可.
9.C
10.B
解:过点B作交MH的延长线于点E, 过点M作于点N,交BE的延长线于点K,如图,
BN=MN,
∠HMB=22.5°,
ME=ME,
在△BNK与△MNH中,
BK=HM=10,
BE=5,
故答案为:B.
过点B作交MH的延长线于点E, 过点M作于点N,交BE的延长线于点K,利用等腰直角三角形的性质得到进而得到BN=MN,利用角的和差求得利用ASA证明,再根据全等三角形的性质得到BE、KE、BK、HM的值,利用三角形的面积公式计算即可求解.
11.C
解:连接ED,如图所示:
∵,,
∴,
即,
∵,
∴,
故答案为:C
先根据四边形的内角和结合对顶角得到,,进而即可得到,即,再根据代入即可求解。
12.A
解:连接AC、BD交于点F
设DE=a,OB=m,
∵BC=2CD,CD=11DE,
∴CD=11a,BC=22a,
∴CE=11a,
∴E(m+22a,10a),F(m+11a,a).
∵矩形ABCD被直线OE分成面积相等的两部分,
∴直线OE过点F.
设直线OE的解析式为y=kx,则有k(m+22a)=10a,k(m+11a)=a,
∴,
∴m=a.
∵线段OB、BC的长为正整数,
∴当22a=9时,m=1是最小值,即a=,
∴S矩形ABCD=BC·CD=22a×11a=22××11×=.
故答案为:A.
连接AC、BD交于点F,设DE=a,OB=m,则CD=11a,BC=22a,CE=11a,E(m+22a,10a),F(m+11a,a),由题意可得直线OE过点F,设直线OE的解析式为y=kx,将点E、F的坐标代入并化简可得m=a,则当a=时,m取得最小值1,然后根据矩形的面积公式进行计算.
13.B
解:,
,
,
,
循环周期为3,
,
.
故答案为:C.
先根据分式的混合运算的运算顺序计算出,得出其循环周期为3,进而得出,即可得到答案.
14.C
15.B
解:∵,且满足,
∴是方程即的两个根,
∴,
∴,,
∴,,
∴;
故答案为:B
先根据题意得到是方程即的两个根,进而根据一元二次方程根与系数的关系得到,进而即可得到,,再根据完全平方公式结合题意即可得到,从而根据即可求解。
16.D
17.②
18.4
解:∵,
∴,
故答案为:4.
先利用估算无理数大小的方法求出,再参照题干中的定义及计算方法分析求解即可.
19.
解:如图所示,延长ID,过点C作CP⊥ID于P,则∠P=90°,∠CDP+∠DCP=90°
∵ 正方形IAKJ的面积为1
∴ AI=1,∠AID=∠P=90°
∵ 正方形ABCD
∴ AD=CD,∠ADC=90°
∴ ∠ADI+∠CDP=90°
∴ ∠ADI=∠DCP
∴
∴ ID=CP,AI=DP=1,
∵ 正方形EFGH
∴ ∠HGF=∠DGC=90°
∵的面积为2,
∴ID·CP=IC·GD=2
∴ ID=CP=2,IP=ID+DP=2+1=3
∴ AD=DC=, IC=
∴ GD=
∵ 正方形是由小正方形和四个全等的直角三角形无缝密铺组成.
∴GD=FC=,GC=
∴GF=CG-GD=
∴ 正方形EFGH的面积= GF2=()2=
本题考查正方形的性质,三角形全等的判定与性质,勾股定理等知识,熟练掌握以上知识,构造“一线三垂直”证三角形全等,得线段长是解题关键。延长ID,过点C作CP⊥ID于P,则∠P=90°,∠CDP+∠DCP=90°,根据正方形IAKJ面积为1得AI=1,证得 ID=CP,AI=DP=1,根据的面积为2,得ID·CP=IC·GD=2, ID=CP=2,IP=3,AD=DC=,
IC=,GD=FC=,GC=得GF=,得正方形EFGH面积为.
20.(1);
(2)
21.(1)解:根据题意,得共3张牌,随机出牌,
∴P(一次出牌小刚出“象”牌)=.
(2)解:在一次出牌小刚胜小明的概率为.
画树状图如图所示.
由树状图可知,可能出现的结果有9种,而且每种结果出现的可能性相同,其中小刚胜小明的结果有3种.
∴P(一次出牌小刚胜小明)=.
(3)解:公平.理由如下:
由树状图可求得P(一次出牌小明胜小刚)=.
∴P(一次出牌小刚胜小明)=P(一次出牌小明胜小刚),即两人获胜的概率相等.
∴这个游戏对小刚和小明公平.
(1)共有3张牌,小刚抽出每张牌的可能性是一样的,故抽出“象”的概率是;
(2)先利用树状图列出所有可能出现的结果,再找出所有符合条件的结果即可求解;
(3)由树状图可求得P(一次出牌小明胜小刚)=,故可判断游戏公平.
22.(1)小华的仰角的正切值为;
(2)两点之间的距离.
23.(1)证明:如图,
∵四边形ABCD、A1B1C1O都是正方形,
∴,,
∴,
∴,
∴,
∴,
在Rt△BEF中,,
∴;
(2)解:仍然成立;
证明:连接AC,
∵O是矩形ABCD的中心,
∴O在AC上,且,
延长EO交CD于G,连接FG,
∵四边形ABCD是矩形,
∴,
∴,
∴,
∴,
又∵矩形A1B1C1O中,,
∴OF垂直平分EG,
∴,
在直角三角形FCG中,,
∴;
(3)解:cm或cm.
解(3)设CE的长为x,
①当点E在线段AC上时,如如:
∵
∴
∵在中,
即,
∵由(2)得:
∴
∴
解得:
∴
②当点E在AC延长线上时,如图:
同理得:
∴
在中,
∴,
解得:
∴,
综上所述: 的长度为cm或cm.
(1)根据正方形的性质及同角的余角相等得∠AOE=∠BOF,从而用ASA证△AOE≌△BOF,得到BE=CF,在Rt△BEF中利用勾股定理即可得证;
(2)连接AC,延长EO交CD于G,连接FG,根据矩形的性质得到∠BAO=∠DCO,∠AEO=∠CGO,用AAS证明△AOE≌△COG,得到AE=CG,OE=OG,最后根据垂直平分线的性质得EF=GF,在Rt△FCG中利用勾股定理即可求解;
(3)分两种情况讨论:①当点E在线段AC上时;②当点E在AC延长线上时;分别利用勾股定理即可求解.
24.(1)解:设乙车间每天生产x个旅行包,则甲车间每天生产2x个旅行包,
∴
∴甲车间每天生产1200个旅行包,乙车间每天生产 600个旅行包.
(2)解:由题意知:甲车间共有:
乙车间共有:
设甲、乙每个车间被抽走了的人数为a,
∴
∴甲、乙每个车间被抽走了的人数为3人.
(1)设乙车间每天生产x个旅行包,则甲车间每天生产2x个旅行包,根据题干"甲车间单独完成这项工作所需的时间比乙车间单独完成少18天",据此列出方程解此方程即可求解;
(2)由题意知:甲车间共有:乙车间共有:设甲、乙每个车间被抽走了的人数为a,根据题干"使抽走工人后甲、乙两车间每天生产的总数之和保持不变",据此列方程解此方程即可求解.
25.(1)解:①连接DM、MC,如图1.
∵OM是⊙P的直径,
∴∠MDO=∠MCO=90°.
∵∠AOB=90°,
∴四边形OCMD是矩形,
∴MD∥OA,MC∥OB,
∴ , .
∵点M是AB的中点,即BM=AM,
∴BD=DO,AC=OC.
∵点M的坐标为(3,4),
∴OB=2OD=8,OA=2OC=6,
∴点B的坐标为(0,8),点A的坐标为(6,0);
②在Rt△AOB中,OA=6,OB=8,
∴AB= =10.
∴BM= AB=5.
∵∠OBM=∠EBD,∠BOM=∠BED,
∴△OBM∽△EBD,
∴ = ,
∴ = ,
∴BE= ,
∴ME=BE﹣BM= ﹣5=
(2)解:连接DP、PE,如图2.
∵ =3,
∴OK=3MK,
∴OM=4MK,PM=2MK,
∴PK=MK.
∵OD=BD,OP=MP,
∴DP∥BM,
∴∠PDK=∠MEK,∠DPK=∠EMK.
在△DPK和△EMK中,
,
∴△DPK≌△EMK,
∴DK=EK.
∵PD=PE,
∴PK⊥DE,
∴cos∠DPK= = ,
∴∠DPK=60°,
∴∠DOM=30°.
∵∠AOB=90°,AM=BM,
∴OM=BM,
∴∠OBA=∠DOM=30°
(3)解:y关于x的函数解析式为y= .
提示:连接PD、OE,如图3.
设MK=t,则有OK=yt,OM=(y+1)t,
BM=OM=(y+1)t,DP=PM= ,
PK= ﹣t= .
由DP∥BM可得△DKP∽△EKM,
则有 = ,可得ME= t.
∵OM是⊙P的直径,
∴∠OEM=90°,
∴OE2=OM2﹣ME2=[(y+1)t]2﹣[ t]2= (y2﹣2y),
即OE= ,
BE=BM+ME=(y+1)t+ t= ,
∴x=tan∠OBA= = ,
∴x2= =1﹣ ,
整理得:y= .
(1)①连接DM、MC,如图1,易证四边形OCMD是矩形,从而得到MD∥OA,MC∥OB,由点M是AB的中点即可得到BD=DO,AC=OC,然后利用点M的坐标就可解决问题;②根据勾股定理可求出AB的长,从而得到BM的长,要求ME的长,只需求BE的长,只需证△OBM∽△EBD,然后运用相似三角形的性质即可;(2)连接DP、PE,如图2,由 =3可得OK=3MK,进而得到OM=4MK,PM=2MK,PK=MK.易证△DPK≌△EMK,则有DK=EK.由PD=PE可得PK⊥DE,从而可得cos∠DPK= = ,则有∠DPK=60°,根据圆周角定理可得∠DOM=30°.由∠AOB=90°,AM=BM可得OM=BM,即可得到∠OBA=∠DOM=30°;(3)连接PD、OE,如图3,设MK=t,则有OK=yt,OM=(y+1)t,BM=OM=(y+1)t,DP=PM= ,PK= .由DP∥BM可得△DKP∽△EKM,则有 = ,由此可得ME= t,从而可求得OE= ,BE= ,则有x=tan∠OBA= = ,即x2= =1﹣ ,整理得y= .
26.(1)解:把,代入,得
解这个方程组,得
所以该抛物线得表达式为
(2)解:
过D作轴交BC于H,由,易知:BC解析式为:
设,则。
则
当时,DH最大值为
;此时
(3)解:
,,,
由。
点右移一格和原点重合,故平移后解析式为:
,
联立两函数求解得:,,则
设,则;,
若,则
(1)利用待定系数法求得a,b的值,即可求解;
(2)过D作轴交BC于H,由,先求得BC解析式为:,设出点D、H的坐标,进而表示出DH的表达式,利用二次函数的性质即可求解;
(3)先 由点右移一格和原点重合,求得平移后的表达式 联立两函数求解得:,,进而得到, 设,则 ,,,根据, 解得m的值,从而求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
机密★启用前
2025 年 河 北 中 考 一 模 猜 题 卷
数 学
〈全卷满分120 分, 考试时间120 分钟)
注意事项
1.答题前, 考生务必将姓名、准考证号填写在试卷和答题卡上·
2 .考生作答时, 请在答题卡上作答〈答题注意事项见答题卡), 在本试卷、草稿纸上作答无效。
3 .不能使用计算器。
4 .考试结束后, 将本试卷和答题卡一并交回·
一、选择题(本大题共16个小题,共38分.1~6小题各3分,7~16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.1,0,,四个数中,最大的数是( )
A.1 B.0 C. D.
2.下列计算正确的是( )
A. B.
C. D.
3.下列命题中,假命题的是( )
A.面积相等的两个三角形全等
B.等腰三角形的顶角平分线垂直于底边
C.在同一平面内,垂直于同一条直线的两条直线平行
D.三角形的一个外角大于任何一个与它不相邻的内角
4.若二次根式有意义,则x的取值范围是( )
A. B. C. D.
5.要求画的边上的高.下列画法中,正确的是( )
A. B.
C. D.
6.五个大小相同的正方体搭成的几何体如图所示,其主视图是( )
A. B.
C. D.
7.小丽要把一篇文章录入电脑,如图是录入时间(分钟)与录字速度(字/分钟)成反比例函数的图象,该图象经过点.根据图象可知,下列说法不正确的是( )
A.这篇文章一共1500字.
B.当小丽的录字速度为75字/分钟时,录入时间为20分钟.
C.小丽在19:20开始录入,要求完成录入时不超过19:35,则小丽每分钟至少应录入90字.
D.小丽原计划每分钟录入125字,实际录入速度比原计划提高了,则小丽会比原计划提前2分钟完成任务.
8. 已知实数a,b,c在数轴上的对应点的位置如图所示,化简|a-b|+|b-c|-|c-a|的结果是 ( )
A.a-b B.b+c C.0 D.a-c
9.下列方程中,有实数解的方程是( )
A. B.
C. D.
10.如图,在等腰 Rt△ABC 中,BC=AC,H、M 两点分别在 BC、BA 上,且∠HMB=22.5°,若 HM=10, 则△BHM 的面积是( ).
A.20 B.25 C.26 D.30
11.如图所示,( )
A. B. C. D.
12.如图,矩形被直线分成面积相等的两部分,,若线段的长是正整数,则矩形面积的最小值是( )
A. B.81 C. D.121
13.已知,且,,…,则为( )
A. B. C. D.
14.扇文化是中华优秀传统文化的组成部分,在我国有着深厚的底蕴.如图,某折扇张开的角度为时,扇面面积为、该折扇张开的角度为时,扇面面积为,若,则与关系的图象大致是( )
A. B.
C. D.
15.已知实数,且满足,,则的值为( )
A. B. C. D.
16.如图所示,直线与双曲线交于点A,将直线向上平移4个单位长度后,与y轴交于点C,与双曲线交干点B,若,则k的值为( )
A.3 B.6 C.1 D.
二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分)
17.“科学用眼,保护视力”是青少年珍爱生命的具体表现.某班50名同学的视力检查数据如表所示,其中有两个数据被墨汁遮盖了,以下关于视力的统计量中可以确定的是 (填写正确的序号).
视力 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 3 3 6 9 12 10
①平均数 ②众数 ③方差
18.规定用符号表示一个实数的整数部分,例如:,,按此规定的值为 .
19.勾股定理的证明方法多样.如图正方形是由小正方形和四个全等的直角三角形无缝密铺组成.延长交以为直径的圆于点(点在的上侧),连结,.分别以,为边向外作正方形,.已知的面积为2,正方形的面积为1,则正方形的面积为 .
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
20.如图,数轴上点,,对应的数分别为,,,且,将点向左移动个单位长度到达点,将点向右移动个单位长度到达点.
(1)_______,_______;
(2)若将数轴折叠,使得点与点重合,求与点重合的点表示的数.
21. 小刚和小明两位同学玩一种游戏.游戏规则为:两人各执“象、虎、鼠”三张牌,同时各出一张牌定胜负,其中象胜虎、虎胜鼠、鼠胜象,若两人所出牌相同,则为平局.例如,小刚出象牌,小明出虎牌,则小刚胜;又如,两人同时出象牌,则两人平局.
(1)一次出牌小刚出“象”牌的概率是多少.
(2)如果用A,B,C分别表示小刚的象、虎、鼠三张牌,用A1,B1,C1分别表示小明的象、虎、鼠三张牌,那么一次出牌小刚胜小明的概率是多少 用列表法或画树状图法加以说明.
(3)你认为这个游戏对小刚和小明公平吗 为什么
22.随着数字转型世界大会的召开,引领时尚,无人机走进人们生活.周末小华利用无人机来测量汶河上,两点之间的距离(,位于同一水平地面上),如图所示,小华站在处遥控空中处的无人机,此时他的仰角为,无人机的飞行高度为,并且无人机测得河岸边处的俯角为,若小华的身高,(点,,,在同一平面内).
(1)求小华的仰角的正切值;
(2)求、两点之间的距离.
23. 如图
(1)【探索发现】如图1,正方形的对角线相交于点O,点O又是正方形的一个顶点,而且这两个正方形的边长相等,我们知道,无论正方形绕点O怎么转动,总有,连接,求证:.
(2)【类比迁移】如图2,矩形的中心O是矩形的一个顶点,与边相交于点E,与边相交于点F,连接,矩形可绕着点O旋转,判断(1)中的结论是否成立,若成立,请证明,若不成立,请说明理由;
(3)【迁移拓展】如图3,在中,,,,直角的顶点D在边的中点处,它的两条边和分别与直线相交于点E,F,可绕着点D旋转,当时,直接写出线段的长度.
24.[应用意识]某包装公司承接到 21 600 个旅行包的订单,准备将任务分配给甲、乙两个车间去完成.由于他们的设备与人数不同,甲车间每天生产的总数是乙车间每天生产总数的2倍,甲车间单独完成这项工作所需的时间比乙车间单独完成少 18 天.
(1)问甲、乙车间每天分别生产多少个旅行包
(2)若已知甲车间每人每天生产 60个旅行包,乙车间每人每天生产 40个旅行包.因另有紧急任务,公司决定在甲、乙两车间抽走相等数量的工人.为了使抽走工人后甲、乙两车间每天生产的总数之和保持不变,余下的所有工人每天的生产个数需要提高 20%,求甲、乙每个车间被抽走了的人数.
25.如图,在平面直角坐标系中,点M是第一象限内一点,过M的直线分别交x轴,y轴的正半轴于A,B两点,且M是AB的中点.以OM为直径的⊙P分别交x轴,y轴于C,D两点,交直线AB于点E(位于点M右下方),连结DE交OM于点K.
(1)若点M的坐标为(3,4),
①求A,B两点的坐标;
②求ME的长.
(2)若 =3,求∠OBA的度数.
(3)设tan∠OBA=x(0<x<1), =y,直接写出y关于x的函数解析式.
26.如图,抛物线与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,点A、B的坐标为,
图1 图2
(1)如图1,求抛物线的解析式;
(2)如图1,点D在直线BC上方的抛物线上运动(不含端点B、C),连接DC、DB,当△BCD面积最大时,求出面积最大值和点D的坐标;
(3)如图2,将(1)中的抛物线向右平移,当它恰好经过原点时,设原抛物线与平移后的抛物线交于点E,连接BE.点M为原抛物线对称轴上一点,以B、E、M为顶点的三角形是直角三角形时,写出所有符合条件的点M的坐标,并写出求解点M的坐标的其中一种情况.
答案解析部分
1.A
解:由题意可得:
-12<-2<0<1
故答案为:A
直接比较大小即可求出答案.
2.D
3.A
4.B
5.C
解:A、图中为边上的高,不符合题意;
B、图中不是高,不符合题意;
C、图中为边上的高,符合题意;
D、图中为边上的高,不符合题意;
故选:C.
根据从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高,逐项分析即可求解.
6.A
7.C
8.C
解:根据题意可得:c<0
∴|a-b|+|b-c|-|c-a|=a-b+b-c-(a-c)=a-b+b-c-a+c=0,
故答案为:C.
先根据题意及数轴判断出a-b>0,b-c>0,c-a<0,再去掉绝对值,最后合并同类项即可.
9.C
10.B
解:过点B作交MH的延长线于点E, 过点M作于点N,交BE的延长线于点K,如图,
BN=MN,
∠HMB=22.5°,
ME=ME,
在△BNK与△MNH中,
BK=HM=10,
BE=5,
故答案为:B.
过点B作交MH的延长线于点E, 过点M作于点N,交BE的延长线于点K,利用等腰直角三角形的性质得到进而得到BN=MN,利用角的和差求得利用ASA证明,再根据全等三角形的性质得到BE、KE、BK、HM的值,利用三角形的面积公式计算即可求解.
11.C
解:连接ED,如图所示:
∵,,
∴,
即,
∵,
∴,
故答案为:C
先根据四边形的内角和结合对顶角得到,,进而即可得到,即,再根据代入即可求解。
12.A
解:连接AC、BD交于点F
设DE=a,OB=m,
∵BC=2CD,CD=11DE,
∴CD=11a,BC=22a,
∴CE=11a,
∴E(m+22a,10a),F(m+11a,a).
∵矩形ABCD被直线OE分成面积相等的两部分,
∴直线OE过点F.
设直线OE的解析式为y=kx,则有k(m+22a)=10a,k(m+11a)=a,
∴,
∴m=a.
∵线段OB、BC的长为正整数,
∴当22a=9时,m=1是最小值,即a=,
∴S矩形ABCD=BC·CD=22a×11a=22××11×=.
故答案为:A.
连接AC、BD交于点F,设DE=a,OB=m,则CD=11a,BC=22a,CE=11a,E(m+22a,10a),F(m+11a,a),由题意可得直线OE过点F,设直线OE的解析式为y=kx,将点E、F的坐标代入并化简可得m=a,则当a=时,m取得最小值1,然后根据矩形的面积公式进行计算.
13.B
解:,
,
,
,
循环周期为3,
,
.
故答案为:C.
先根据分式的混合运算的运算顺序计算出,得出其循环周期为3,进而得出,即可得到答案.
14.C
15.B
解:∵,且满足,
∴是方程即的两个根,
∴,
∴,,
∴,,
∴;
故答案为:B
先根据题意得到是方程即的两个根,进而根据一元二次方程根与系数的关系得到,进而即可得到,,再根据完全平方公式结合题意即可得到,从而根据即可求解。
16.D
17.②
18.4
解:∵,
∴,
故答案为:4.
先利用估算无理数大小的方法求出,再参照题干中的定义及计算方法分析求解即可.
19.
解:如图所示,延长ID,过点C作CP⊥ID于P,则∠P=90°,∠CDP+∠DCP=90°
∵ 正方形IAKJ的面积为1
∴ AI=1,∠AID=∠P=90°
∵ 正方形ABCD
∴ AD=CD,∠ADC=90°
∴ ∠ADI+∠CDP=90°
∴ ∠ADI=∠DCP
∴
∴ ID=CP,AI=DP=1,
∵ 正方形EFGH
∴ ∠HGF=∠DGC=90°
∵的面积为2,
∴ID·CP=IC·GD=2
∴ ID=CP=2,IP=ID+DP=2+1=3
∴ AD=DC=, IC=
∴ GD=
∵ 正方形是由小正方形和四个全等的直角三角形无缝密铺组成.
∴GD=FC=,GC=
∴GF=CG-GD=
∴ 正方形EFGH的面积= GF2=()2=
本题考查正方形的性质,三角形全等的判定与性质,勾股定理等知识,熟练掌握以上知识,构造“一线三垂直”证三角形全等,得线段长是解题关键。延长ID,过点C作CP⊥ID于P,则∠P=90°,∠CDP+∠DCP=90°,根据正方形IAKJ面积为1得AI=1,证得 ID=CP,AI=DP=1,根据的面积为2,得ID·CP=IC·GD=2, ID=CP=2,IP=3,AD=DC=,
IC=,GD=FC=,GC=得GF=,得正方形EFGH面积为.
20.(1);
(2)
21.(1)解:根据题意,得共3张牌,随机出牌,
∴P(一次出牌小刚出“象”牌)=.
(2)解:在一次出牌小刚胜小明的概率为.
画树状图如图所示.
由树状图可知,可能出现的结果有9种,而且每种结果出现的可能性相同,其中小刚胜小明的结果有3种.
∴P(一次出牌小刚胜小明)=.
(3)解:公平.理由如下:
由树状图可求得P(一次出牌小明胜小刚)=.
∴P(一次出牌小刚胜小明)=P(一次出牌小明胜小刚),即两人获胜的概率相等.
∴这个游戏对小刚和小明公平.
(1)共有3张牌,小刚抽出每张牌的可能性是一样的,故抽出“象”的概率是;
(2)先利用树状图列出所有可能出现的结果,再找出所有符合条件的结果即可求解;
(3)由树状图可求得P(一次出牌小明胜小刚)=,故可判断游戏公平.
22.(1)小华的仰角的正切值为;
(2)两点之间的距离.
23.(1)证明:如图,
∵四边形ABCD、A1B1C1O都是正方形,
∴,,
∴,
∴,
∴,
∴,
在Rt△BEF中,,
∴;
(2)解:仍然成立;
证明:连接AC,
∵O是矩形ABCD的中心,
∴O在AC上,且,
延长EO交CD于G,连接FG,
∵四边形ABCD是矩形,
∴,
∴,
∴,
∴,
又∵矩形A1B1C1O中,,
∴OF垂直平分EG,
∴,
在直角三角形FCG中,,
∴;
(3)解:cm或cm.
解(3)设CE的长为x,
①当点E在线段AC上时,如如:
∵
∴
∵在中,
即,
∵由(2)得:
∴
∴
解得:
∴
②当点E在AC延长线上时,如图:
同理得:
∴
在中,
∴,
解得:
∴,
综上所述: 的长度为cm或cm.
(1)根据正方形的性质及同角的余角相等得∠AOE=∠BOF,从而用ASA证△AOE≌△BOF,得到BE=CF,在Rt△BEF中利用勾股定理即可得证;
(2)连接AC,延长EO交CD于G,连接FG,根据矩形的性质得到∠BAO=∠DCO,∠AEO=∠CGO,用AAS证明△AOE≌△COG,得到AE=CG,OE=OG,最后根据垂直平分线的性质得EF=GF,在Rt△FCG中利用勾股定理即可求解;
(3)分两种情况讨论:①当点E在线段AC上时;②当点E在AC延长线上时;分别利用勾股定理即可求解.
24.(1)解:设乙车间每天生产x个旅行包,则甲车间每天生产2x个旅行包,
∴
∴甲车间每天生产1200个旅行包,乙车间每天生产 600个旅行包.
(2)解:由题意知:甲车间共有:
乙车间共有:
设甲、乙每个车间被抽走了的人数为a,
∴
∴甲、乙每个车间被抽走了的人数为3人.
(1)设乙车间每天生产x个旅行包,则甲车间每天生产2x个旅行包,根据题干"甲车间单独完成这项工作所需的时间比乙车间单独完成少18天",据此列出方程解此方程即可求解;
(2)由题意知:甲车间共有:乙车间共有:设甲、乙每个车间被抽走了的人数为a,根据题干"使抽走工人后甲、乙两车间每天生产的总数之和保持不变",据此列方程解此方程即可求解.
25.(1)解:①连接DM、MC,如图1.
∵OM是⊙P的直径,
∴∠MDO=∠MCO=90°.
∵∠AOB=90°,
∴四边形OCMD是矩形,
∴MD∥OA,MC∥OB,
∴ , .
∵点M是AB的中点,即BM=AM,
∴BD=DO,AC=OC.
∵点M的坐标为(3,4),
∴OB=2OD=8,OA=2OC=6,
∴点B的坐标为(0,8),点A的坐标为(6,0);
②在Rt△AOB中,OA=6,OB=8,
∴AB= =10.
∴BM= AB=5.
∵∠OBM=∠EBD,∠BOM=∠BED,
∴△OBM∽△EBD,
∴ = ,
∴ = ,
∴BE= ,
∴ME=BE﹣BM= ﹣5=
(2)解:连接DP、PE,如图2.
∵ =3,
∴OK=3MK,
∴OM=4MK,PM=2MK,
∴PK=MK.
∵OD=BD,OP=MP,
∴DP∥BM,
∴∠PDK=∠MEK,∠DPK=∠EMK.
在△DPK和△EMK中,
,
∴△DPK≌△EMK,
∴DK=EK.
∵PD=PE,
∴PK⊥DE,
∴cos∠DPK= = ,
∴∠DPK=60°,
∴∠DOM=30°.
∵∠AOB=90°,AM=BM,
∴OM=BM,
∴∠OBA=∠DOM=30°
(3)解:y关于x的函数解析式为y= .
提示:连接PD、OE,如图3.
设MK=t,则有OK=yt,OM=(y+1)t,
BM=OM=(y+1)t,DP=PM= ,
PK= ﹣t= .
由DP∥BM可得△DKP∽△EKM,
则有 = ,可得ME= t.
∵OM是⊙P的直径,
∴∠OEM=90°,
∴OE2=OM2﹣ME2=[(y+1)t]2﹣[ t]2= (y2﹣2y),
即OE= ,
BE=BM+ME=(y+1)t+ t= ,
∴x=tan∠OBA= = ,
∴x2= =1﹣ ,
整理得:y= .
(1)①连接DM、MC,如图1,易证四边形OCMD是矩形,从而得到MD∥OA,MC∥OB,由点M是AB的中点即可得到BD=DO,AC=OC,然后利用点M的坐标就可解决问题;②根据勾股定理可求出AB的长,从而得到BM的长,要求ME的长,只需求BE的长,只需证△OBM∽△EBD,然后运用相似三角形的性质即可;(2)连接DP、PE,如图2,由 =3可得OK=3MK,进而得到OM=4MK,PM=2MK,PK=MK.易证△DPK≌△EMK,则有DK=EK.由PD=PE可得PK⊥DE,从而可得cos∠DPK= = ,则有∠DPK=60°,根据圆周角定理可得∠DOM=30°.由∠AOB=90°,AM=BM可得OM=BM,即可得到∠OBA=∠DOM=30°;(3)连接PD、OE,如图3,设MK=t,则有OK=yt,OM=(y+1)t,BM=OM=(y+1)t,DP=PM= ,PK= .由DP∥BM可得△DKP∽△EKM,则有 = ,由此可得ME= t,从而可求得OE= ,BE= ,则有x=tan∠OBA= = ,即x2= =1﹣ ,整理得y= .
26.(1)解:把,代入,得
解这个方程组,得
所以该抛物线得表达式为
(2)解:
过D作轴交BC于H,由,易知:BC解析式为:
设,则。
则
当时,DH最大值为
;此时
(3)解:
,,,
由。
点右移一格和原点重合,故平移后解析式为:
,
联立两函数求解得:,,则
设,则;,
若,则
(1)利用待定系数法求得a,b的值,即可求解;
(2)过D作轴交BC于H,由,先求得BC解析式为:,设出点D、H的坐标,进而表示出DH的表达式,利用二次函数的性质即可求解;
(3)先 由点右移一格和原点重合,求得平移后的表达式 联立两函数求解得:,,进而得到, 设,则 ,,,根据, 解得m的值,从而求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
