2025年中考数学一模猜题卷(吉林省专用)—2025年全国各地市最新中考数学模拟考试(含答案)
文档属性
| 名称 | 2025年中考数学一模猜题卷(吉林省专用)—2025年全国各地市最新中考数学模拟考试(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 20:55:40 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
机密★启用前
2025 年 吉 林 省 中 考 一 模 猜 题 卷
数 学
数试卷共7 页,包括六道大题,共26 道小题,全卷满分120分·考试时间为120分钟,考试结束后,将本试卷和答题卡一并交回,
注意事项:
1.答题前考生务必将姓名、准考证号填写在答题卡上, 并将条形码准确粘贴在条形码区域内。
2.答题时, 考生务必按照考试要求在答题卡上的指定区域内作答, 在草稿纸、试卷上答题无效。
一、单项选择题(每小题2分,共12分)
1.如图,下列结论正确的是( )
A. B.
C. D.
2. 2023年3月27日,国际学术期刊《自然·地球科学》刊发的一一篇文章称,中英学者在嫦娥五号月球样品中,测量到撞击玻璃珠中的水,科研团队结合月球全球尺度月壤厚度分析,推测出月壤的储水量最高约 270000000000 吨.数 270000000000用科学记数法表示为( )
A. B. C. D.
3.要制作一个“爱我中华”的展板,如图所示,用板制作的“中”字的俯视图是( )
A. B.
C. D.
4.关于的一元二次方程的一个根是,则的值为( )
A. B. C.或 D.
5.如图,矩形的顶点A、B分别在轴,轴上,,将矩形绕点顺时针旋转,每次旋转,则第2024次旋转结束时,点的坐标为( )
A. B. C. D.
6.如图,四边形内接于,如果它的一个外角,那么( )
A. B. C. D.
二、填空题(每小题3分,共24分)
7.已知,满足,则的值为 .
8.因式分解:t3s﹣ts= .
9.若关于x的不等式组的解集为,且关于m,n方程组的解满足,则所有满足条件的整数a的值之积为 .
10.如图,在矩形中,,,点在上且点为的中点,点为边上的一个动点,为的中点,则的最小值为 .
11.“香渡栏干屈曲,红妆映、薄绮疏棂.”图1窗棂的外边框为正六边形(如图2),则该正六边形的每个内角为 .
12.图,在正方形ABCD中,点E是对角线AC上一点,且AE=2CE,点H为边AB上一点,且BH=2AH,连接DH与AC相交于点G,过点E作EF⊥DH于点F,若AB的长为6,则EF的长为 。
13.南宋数学家杨辉所著《田亩比类乘除捷法》中记载:“直田积八百六十四步,只云长阔共六十步,问长及阔各几步.”译文:一块矩形田地的面积是864平方步,它的长和宽共60步,问它的长和宽各是多少步?设这块矩形田地的长为步,根据题意可列方程为 .
14.如图,在正方形中,,以为圆心,为半径作圆弧,交的延长线于点,连结.则图中阴影部分的面积为 .
三、解答题(每小题5分,共20分)
15.(1) 先化简, 再求值: , 其中 , .
已知 , 求代数式 的值.
16.一个盒子里装有3个只有颜色不同的球,其中2个红球,1个白球.
(1)若只从盒子里摸出一个球,直接写出摸出一个白球的概率是________.
(2)若从盒子里摸出一个球,记下颜色后放回,并搅匀,再摸出一个球,求两次摸出都是红球的概率.
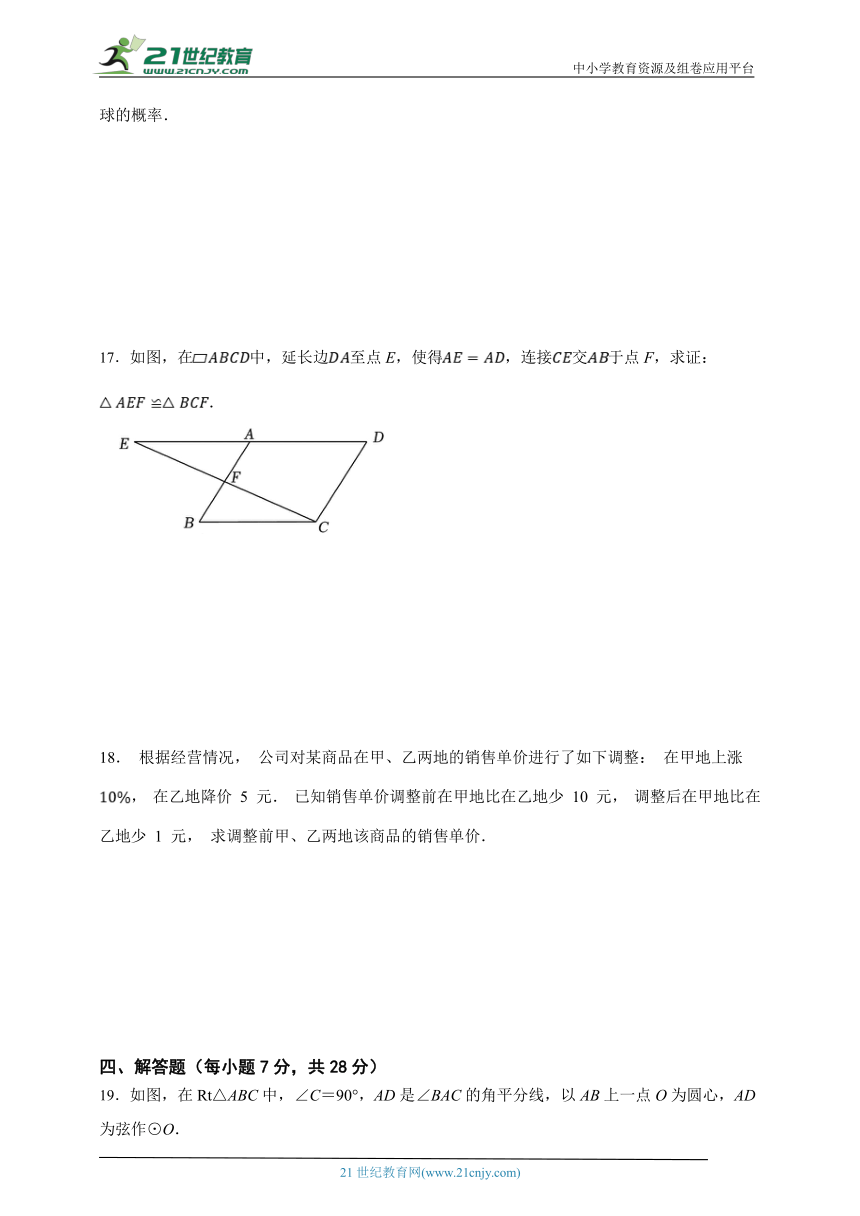
17.如图,在中,延长边至点E,使得,连接交于点F,求证:.
根据经营情况, 公司对某商品在甲、乙两地的销售单价进行了如下调整: 在甲地上涨 , 在乙地降价 5 元. 已知销售单价调整前在甲地比在乙地少 10 元, 调整后在甲地比在乙地少 1 元, 求调整前甲、乙两地该商品的销售单价.
四、解答题(每小题7分,共28分)
19.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.
(1)尺规作图:作出⊙O(不写作法与证明,保留作图痕迹);
(2)求证:BC为⊙O的切线.
20.科学课上,同学用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度是关于液体的密度的反比例函数,当密度计悬浮在密度为的水中时,.
(1)求关于的函数解析式.
(2)当密度计悬浮在另一种液体中时,,求该液体的密度.
21.社会消费品零售总额按消费类型可划分为商品零售和餐饮收入,它是表现国内消费需求最直接的数据,也是研究国内零售市场变动情况、反映经济景气程度的重要指标.如图所示是我国2019年1-2月—2023年1-2月按消费类型分零售额同比增速以及社会消费品零售总额的统计图.
请根据以上信息,解答下列问题:
(1)2019年1-2月—2023年1-2月我国社会消费品零售总额的中位数是 亿元;
(2)根据国家统计局数据显示,2022年1-2月我国商品零售66708亿元,求2023年1-2月我国的餐饮收入;(结果保留整数)
(3)写出一条关于我国2019年1-2月—2023年1-2月期间我国社会消费品零售总额变化趋势的信息.
22.如图,热气球的探测器显示,从热气球底部A处看一栋高楼顶部的仰角为30° ,看这栋楼底部的俯角为60° ,热气球A处与高楼的水平距离为120m.
(1)求∠ABC的角度;
(2)这栋高楼有多高?(结果保留根号)
五、解答题(每小题8分,共16分)
23.综合与实践:有一科技小组进行了机器人行走性能试验.在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分钟的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图像,回答下列问题:
(1)A、B两点之间的距离是 米,甲机器人前2分钟的速度为 米/分;
(2)已知线段轴,前3分钟甲机器人的速度不变.
①在3~4分钟的这段时间,甲机器人的速度为 ▲ 米/分.
②请直接写出在整个运动过程中,两机器人相距时x的值.
24.定义:把斜边重合,且直角顶点不重合的两个直角三角形叫做共边直角三角形.
(1)概念理解:如图1.在和中,,,,,,说明和是共边直角三角形.
(2)问题探究:如图2,和是共边直角三角形,E、F分别是BC、AD的中点,连接EF,求证.
(3)拓展延伸:如图3,和是共边直角三角形,且,连接AD,求证:平分.
六、解答题(每小题10分,共20分)
25.如图,已知矩形ABCD的边长,.某一时刻,动点M从A点出发沿AB方向以的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.
26.根据以下素材,探索完成任务。
运用二次函数研究电缆架设问题
素材1 电缆在空中架设时,两端挂起的电缆下垂都可以近似地看成抛物线的形状.如图,在一个斜坡 BD上按水平距离间隔90m架设两个塔柱,每个塔柱固定电缆的位置离地面高度为20m(AB=CD=20m),按如图所示的方式建立平面直角坐标系(x轴在水平方向上).点A,O,E 在同一水平线上,经测量,AO=60m,斜坡BD的坡比为1:10.
素材2 若电缆下垂的安全高度是13.5m,即电缆距离坡面铅直高度的最小值不小于13.5m时,符合安全要求,否则存在安全隐患.(说明:直线GH⊥x轴且分别与直线BD和抛物线相交于点H,G.点G 距离坡面的铅直高度为GH 的长)
任务1 确定电缆形状 求点 D 的坐标及下垂电缆的抛物线的函数表达式.
任务2 判断电缆安全 上述这种电缆的架设是否符合安全要求? 请说明理由.
任务3 探究安装方法 工程队想在坡比为1:8的斜坡上架设电缆,两个塔柱的高度仍为20m,电缆抛物线的形状与任务1相同.若电缆下垂恰好符合安全高度要求,则两个塔柱的水平距离应为多少米?
答案解析部分
1.B
解:由数轴可得:,,,
∴,,
∴,,,.
故选:B.
本题考查数轴上数的表示,根据数轴上右侧的数大于左侧的数,得到,,,进而得到,,结合选项,逐项分析判定,即可得到答案.
2.B
解:
故答案为:B.
本题主要考查科学记数法,科学记数法嗯表示形式为:,n为整数,在确定n时,要根据把原来的数,变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,且当原数绝对值10时,n是正数;当原数绝对值时,n为负数,属于基础题型.
3.C
解:由题意可知,该图形的俯视图为:
故选:C
从上往下看展板得到俯视图即可,注意看不见用虚线表示.
4.B
5.C
6.A
7.
8.ts(t+1)(t-1)
解:原式=ts(t2-1)
=ts(t+1)(t-1),
故答案为:ts(t+1)(t-1) .
先提公因式后,然后根据平方差公式因式分解即可.
9.
10.
11.120°
解:∵正六边形各个内角的度数相同,
故该正六边形的每个内角为.
故答案为:120°.
根据多边形的内角和公式求出内角和,再利用正六边形的性质求每个内角度数即可.
12.
解:过E作于M,连结,如图所示:
∵,
∴,
∵四边形为正方形,
∴,
∴,
∴,
∴,
∴,
在中,,
∵,
∴,
在中, ,
∵,
∴,
∵,
∴,
∴,
∴,
∵为正方形的对角线,,
∵,
∴,
∴,
在中,,
解得:,
在中,,
设,
∵,
∴,
即,
解得,
在中,.
故答案为:
过E作于M,连结,先根据正方形的性质得到,进而根据等腰三角形的性质结合平行线的性质得到,再根据相似三角形的判定与性质证明得到,从而得到,根据勾股定理求出DH,进而求出AC,再根据题意表示出AM,EM,AE,从而根据勾股定理即可求出EM,再求出EH,设,根据勾股定理结合题意进行线段的运算即可求解。
13.
解:设矩形田地的长为x步,则宽为60-x步,根据题意,可得:x(60-x)=864
本题考查一元二次方程的实际应用古代数学问题。结合题意,找准数量关系,列出一元二次方程即可。
14.
15.(1)解:
=
=
,
(2)解:
=
=
=
(1)利用平方差公式,整式的混合运算化简为,然后代数求值即可;
(2)利用完全平方公式,整式的混合运算化简为,由题意,即可得到答案.
16.(1)
(2)
17.证明:在中,∵,,
∴,
∵,
∴,
在与中,
∴.
根据平行线的性质求出 , 再求出AE=BC,最后利用AAS证明三角形全等即可。
18.解:设调整前甲地该商品的销售单价为x元,乙地该商品的销售单价为y元,
根据题意可知,
解得,
答:调整前甲地该商品的销售单价为40元,乙地该商品的销售单价为50元
设调整前甲地该商品的销售单价为x元,乙地该商品的销售单价为y元,则调整后甲地的单价为(1+10%)x元,乙地的价格为(Y+5)元,根据销售单价调整前在甲地比在乙地少10元, 调整后在甲地比在乙地少1元,即可列出关于x,y的二元一次方程组,解方程组即可得到答案.
19.(1)解:如图所示,⊙O即为所求;
(2)证明:连接OD.
∵OA=OD,
∴∠OAD=∠ODA,
∵AD是∠BAC的角平分线,
∴∠CAD=∠OAD,
∴∠ODA=∠CAD,
∴OD∥AC.
又∵∠C=90°,
∴∠ODB=90°,
∴BC是⊙O的切线.
(1)作AD垂直平分线交AB于点O,点O即为圆心,即可求解;
(2)连接OD,根据等腰三角形的性质得到然后根据角平分线的定义得到,进而可证明即可证明BC为⊙O的切线.
20.(1)解:设h关于的函数解析式为,
将代入解析式,
可得:k=1×20=20,
∴h关于的函数解析式为 .
(2)解:将代入,
可得:,
解得:.
答:该液体的密度为 .
(1)结合题干中的数据,利用待定系数法求出函数解析式即可;
(2)将代入, 再求出即可.
21.(1)69737
(2)解:由图②可知2022年1-2月社会消费品总额为74426亿元.
∵2022年1-2月我国商品零售66708亿元,
∴2022年1-2月我国餐饮收入为
74426-66708=7718(亿元).
∵由图①可知2023年1-2月餐饮收入增长率为9.2%,
∴2023年1-2月我国的餐饮收入为
7718×(1+9.2%)=8428.056≈8428(亿元).
(3)解:2019年1-2月—2020年1-2月我国社会消费品零售总额有所降低,之后几年都在增高.
解:(1)将我国社会消费品零售总额按从小到大的顺序排列为52130,66064,69737,74426,77067,
∴中位数是69737亿元,
故答案为:69737;
(1)根据题意将数据从小到大排列,进而取最中间的数即可得到中位数;
(2)由图②可知2022年1-2月社会消费品总额为74426亿元,进而即可求出2022年1-2月我国餐饮收入,再根据图①即可求解;
(3)根据折线统计图即可求解.
22.(1)解:过点A作AD⊥BC,垂足为D.
(2)解:在RtΔABD中,
在Rt中,
(1)过点A作AD⊥BC,垂足为D,根据题意进行角的运算得到∠ABC的度数;
(2)根据正切函数即可得到BD,进而根据特殊角的三角函数值结合正切函数即可求出CD,再根据BC=BD+CD即可求解。
23.(1)70;95
(2)解:①60;②1.2分或2.8分或4.6分
解:(1)由图像可知,A、B两点之间的距离是70米,
甲机器人前2分钟的速度为:(米/分),
故答案为:70,95;
(2)①∵,乙机器人始终以60米/分钟的速度行走,
∴甲、乙机器人的速度都是60米/分钟;
故答案为:60,
②当时,
解得,,
当时,
,
当时,设甲、乙两机器人之间的距离y米与他们的行走时间x分钟之间函数解析式为,
将点和点代入,得
解得,,
即函数解析式为,
令,得,
,
即两机器人出发1.2分钟,2.8分钟,4.6分钟时相距28米.
(1)找出图象的最高点对应的纵坐标的值即为A、B两点之间的距离,结合图形可得甲机器人前2分钟的路程为(70+60×2)米,然后根据路程÷时间=速度进行解答;
(2)①由图形可得乙机器人始终以60米/分钟的速度行走,据此解答;
②当0≤x≤2时,根据70-甲、乙x分钟的路程差=28建立方程,求解即可;当224.(1)证明:∵在中,,,,∴
∵,
∴
∴是直角三角形,
和是共边直角三角形;
(2)证明:如图,连接AE,DE,
∵E点是BC中点,
∴AE,DE分别是和斜边上的中线,
∴,∴
∴是等腰三角形,
∵F点是AD中点,∴
(3)解:取BC中点Q,连结AQ,DQ
∵
∴
设
则
∵, ,Q为BC中点,∴
∴
∴
∴
∴∴∴AD平分
(1)由勾股定理求出BC=5,然后根据勾股定理逆定理得到是直角三角形,即可得到答案;
(2)连接AE,DE,根据直角三角形斜边上的中线等于斜边的一半,得,然后根据等腰三角形三线合一的性质即可求解;
(3)取BC中点Q,连结AQ,DQ,由题意得,设,则,, ,推出,由可推出,即可得到答案.
25.存在.当或时,以、、为顶点的三角形与相似
26.解:任务1:如图,作,易证四边形ABFE是矩形,
,
, 斜坡BD的坡比为1:10 ,
,,
,
,
,
,
设抛物线关系式为,
得,解得,
抛物线关系式为,
点D(30,-11),下垂电缆的抛物线的函数表达式为.
任务2:设直线BD的关系式为,
得,解得,
直线BD的关系式为,
设,
,
当时,,
这种电缆的架设不符合安全要求.
任务3:如图,建立直角坐标系,
设,
,
直线BD的关系式为,
,
,
抛物线关系式为,
设,
,
电缆下垂恰好符合安全高度要求,
,解得,
抛物线关系式为,
代入点,得,
解得,
,
两个塔柱的水平距离应为米.
任务1:作,易证四边形ABFE是矩形,利用矩形的性质分别求得各点坐标,再通过待定系数法求得抛物线关系式.
任务2:设直线BD的关系式为,通过待定系数法求得直线BD的关系式,设,用x表示出GH的长度,再利用二次函数的性质求得当时,GH有最小值小于13.5m,故这种电缆的架设不符合安全要求.
任务3:如图,以点B为原点重新建立直角坐标系,设,则,从而得到直线BD的关系式为,及点A、C的坐标,又电缆抛物线的形状与任务1相同,可得抛物线关系式为,设,表示出GH的长度,再利用二次函数的性质求得GH的最小值,进而解得a的值,最后求得两个塔柱的水平距离.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
机密★启用前
2025 年 吉 林 省 中 考 一 模 猜 题 卷
数 学
数试卷共7 页,包括六道大题,共26 道小题,全卷满分120分·考试时间为120分钟,考试结束后,将本试卷和答题卡一并交回,
注意事项:
1.答题前考生务必将姓名、准考证号填写在答题卡上, 并将条形码准确粘贴在条形码区域内。
2.答题时, 考生务必按照考试要求在答题卡上的指定区域内作答, 在草稿纸、试卷上答题无效。
一、单项选择题(每小题2分,共12分)
1.如图,下列结论正确的是( )
A. B.
C. D.
2. 2023年3月27日,国际学术期刊《自然·地球科学》刊发的一一篇文章称,中英学者在嫦娥五号月球样品中,测量到撞击玻璃珠中的水,科研团队结合月球全球尺度月壤厚度分析,推测出月壤的储水量最高约 270000000000 吨.数 270000000000用科学记数法表示为( )
A. B. C. D.
3.要制作一个“爱我中华”的展板,如图所示,用板制作的“中”字的俯视图是( )
A. B.
C. D.
4.关于的一元二次方程的一个根是,则的值为( )
A. B. C.或 D.
5.如图,矩形的顶点A、B分别在轴,轴上,,将矩形绕点顺时针旋转,每次旋转,则第2024次旋转结束时,点的坐标为( )
A. B. C. D.
6.如图,四边形内接于,如果它的一个外角,那么( )
A. B. C. D.
二、填空题(每小题3分,共24分)
7.已知,满足,则的值为 .
8.因式分解:t3s﹣ts= .
9.若关于x的不等式组的解集为,且关于m,n方程组的解满足,则所有满足条件的整数a的值之积为 .
10.如图,在矩形中,,,点在上且点为的中点,点为边上的一个动点,为的中点,则的最小值为 .
11.“香渡栏干屈曲,红妆映、薄绮疏棂.”图1窗棂的外边框为正六边形(如图2),则该正六边形的每个内角为 .
12.图,在正方形ABCD中,点E是对角线AC上一点,且AE=2CE,点H为边AB上一点,且BH=2AH,连接DH与AC相交于点G,过点E作EF⊥DH于点F,若AB的长为6,则EF的长为 。
13.南宋数学家杨辉所著《田亩比类乘除捷法》中记载:“直田积八百六十四步,只云长阔共六十步,问长及阔各几步.”译文:一块矩形田地的面积是864平方步,它的长和宽共60步,问它的长和宽各是多少步?设这块矩形田地的长为步,根据题意可列方程为 .
14.如图,在正方形中,,以为圆心,为半径作圆弧,交的延长线于点,连结.则图中阴影部分的面积为 .
三、解答题(每小题5分,共20分)
15.(1) 先化简, 再求值: , 其中 , .
已知 , 求代数式 的值.
16.一个盒子里装有3个只有颜色不同的球,其中2个红球,1个白球.
(1)若只从盒子里摸出一个球,直接写出摸出一个白球的概率是________.
(2)若从盒子里摸出一个球,记下颜色后放回,并搅匀,再摸出一个球,求两次摸出都是红球的概率.
17.如图,在中,延长边至点E,使得,连接交于点F,求证:.
根据经营情况, 公司对某商品在甲、乙两地的销售单价进行了如下调整: 在甲地上涨 , 在乙地降价 5 元. 已知销售单价调整前在甲地比在乙地少 10 元, 调整后在甲地比在乙地少 1 元, 求调整前甲、乙两地该商品的销售单价.
四、解答题(每小题7分,共28分)
19.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.
(1)尺规作图:作出⊙O(不写作法与证明,保留作图痕迹);
(2)求证:BC为⊙O的切线.
20.科学课上,同学用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度是关于液体的密度的反比例函数,当密度计悬浮在密度为的水中时,.
(1)求关于的函数解析式.
(2)当密度计悬浮在另一种液体中时,,求该液体的密度.
21.社会消费品零售总额按消费类型可划分为商品零售和餐饮收入,它是表现国内消费需求最直接的数据,也是研究国内零售市场变动情况、反映经济景气程度的重要指标.如图所示是我国2019年1-2月—2023年1-2月按消费类型分零售额同比增速以及社会消费品零售总额的统计图.
请根据以上信息,解答下列问题:
(1)2019年1-2月—2023年1-2月我国社会消费品零售总额的中位数是 亿元;
(2)根据国家统计局数据显示,2022年1-2月我国商品零售66708亿元,求2023年1-2月我国的餐饮收入;(结果保留整数)
(3)写出一条关于我国2019年1-2月—2023年1-2月期间我国社会消费品零售总额变化趋势的信息.
22.如图,热气球的探测器显示,从热气球底部A处看一栋高楼顶部的仰角为30° ,看这栋楼底部的俯角为60° ,热气球A处与高楼的水平距离为120m.
(1)求∠ABC的角度;
(2)这栋高楼有多高?(结果保留根号)
五、解答题(每小题8分,共16分)
23.综合与实践:有一科技小组进行了机器人行走性能试验.在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分钟的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图像,回答下列问题:
(1)A、B两点之间的距离是 米,甲机器人前2分钟的速度为 米/分;
(2)已知线段轴,前3分钟甲机器人的速度不变.
①在3~4分钟的这段时间,甲机器人的速度为 ▲ 米/分.
②请直接写出在整个运动过程中,两机器人相距时x的值.
24.定义:把斜边重合,且直角顶点不重合的两个直角三角形叫做共边直角三角形.
(1)概念理解:如图1.在和中,,,,,,说明和是共边直角三角形.
(2)问题探究:如图2,和是共边直角三角形,E、F分别是BC、AD的中点,连接EF,求证.
(3)拓展延伸:如图3,和是共边直角三角形,且,连接AD,求证:平分.
六、解答题(每小题10分,共20分)
25.如图,已知矩形ABCD的边长,.某一时刻,动点M从A点出发沿AB方向以的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.
26.根据以下素材,探索完成任务。
运用二次函数研究电缆架设问题
素材1 电缆在空中架设时,两端挂起的电缆下垂都可以近似地看成抛物线的形状.如图,在一个斜坡 BD上按水平距离间隔90m架设两个塔柱,每个塔柱固定电缆的位置离地面高度为20m(AB=CD=20m),按如图所示的方式建立平面直角坐标系(x轴在水平方向上).点A,O,E 在同一水平线上,经测量,AO=60m,斜坡BD的坡比为1:10.
素材2 若电缆下垂的安全高度是13.5m,即电缆距离坡面铅直高度的最小值不小于13.5m时,符合安全要求,否则存在安全隐患.(说明:直线GH⊥x轴且分别与直线BD和抛物线相交于点H,G.点G 距离坡面的铅直高度为GH 的长)
任务1 确定电缆形状 求点 D 的坐标及下垂电缆的抛物线的函数表达式.
任务2 判断电缆安全 上述这种电缆的架设是否符合安全要求? 请说明理由.
任务3 探究安装方法 工程队想在坡比为1:8的斜坡上架设电缆,两个塔柱的高度仍为20m,电缆抛物线的形状与任务1相同.若电缆下垂恰好符合安全高度要求,则两个塔柱的水平距离应为多少米?
答案解析部分
1.B
解:由数轴可得:,,,
∴,,
∴,,,.
故选:B.
本题考查数轴上数的表示,根据数轴上右侧的数大于左侧的数,得到,,,进而得到,,结合选项,逐项分析判定,即可得到答案.
2.B
解:
故答案为:B.
本题主要考查科学记数法,科学记数法嗯表示形式为:,n为整数,在确定n时,要根据把原来的数,变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,且当原数绝对值10时,n是正数;当原数绝对值时,n为负数,属于基础题型.
3.C
解:由题意可知,该图形的俯视图为:
故选:C
从上往下看展板得到俯视图即可,注意看不见用虚线表示.
4.B
5.C
6.A
7.
8.ts(t+1)(t-1)
解:原式=ts(t2-1)
=ts(t+1)(t-1),
故答案为:ts(t+1)(t-1) .
先提公因式后,然后根据平方差公式因式分解即可.
9.
10.
11.120°
解:∵正六边形各个内角的度数相同,
故该正六边形的每个内角为.
故答案为:120°.
根据多边形的内角和公式求出内角和,再利用正六边形的性质求每个内角度数即可.
12.
解:过E作于M,连结,如图所示:
∵,
∴,
∵四边形为正方形,
∴,
∴,
∴,
∴,
∴,
在中,,
∵,
∴,
在中, ,
∵,
∴,
∵,
∴,
∴,
∴,
∵为正方形的对角线,,
∵,
∴,
∴,
在中,,
解得:,
在中,,
设,
∵,
∴,
即,
解得,
在中,.
故答案为:
过E作于M,连结,先根据正方形的性质得到,进而根据等腰三角形的性质结合平行线的性质得到,再根据相似三角形的判定与性质证明得到,从而得到,根据勾股定理求出DH,进而求出AC,再根据题意表示出AM,EM,AE,从而根据勾股定理即可求出EM,再求出EH,设,根据勾股定理结合题意进行线段的运算即可求解。
13.
解:设矩形田地的长为x步,则宽为60-x步,根据题意,可得:x(60-x)=864
本题考查一元二次方程的实际应用古代数学问题。结合题意,找准数量关系,列出一元二次方程即可。
14.
15.(1)解:
=
=
,
(2)解:
=
=
=
(1)利用平方差公式,整式的混合运算化简为,然后代数求值即可;
(2)利用完全平方公式,整式的混合运算化简为,由题意,即可得到答案.
16.(1)
(2)
17.证明:在中,∵,,
∴,
∵,
∴,
在与中,
∴.
根据平行线的性质求出 , 再求出AE=BC,最后利用AAS证明三角形全等即可。
18.解:设调整前甲地该商品的销售单价为x元,乙地该商品的销售单价为y元,
根据题意可知,
解得,
答:调整前甲地该商品的销售单价为40元,乙地该商品的销售单价为50元
设调整前甲地该商品的销售单价为x元,乙地该商品的销售单价为y元,则调整后甲地的单价为(1+10%)x元,乙地的价格为(Y+5)元,根据销售单价调整前在甲地比在乙地少10元, 调整后在甲地比在乙地少1元,即可列出关于x,y的二元一次方程组,解方程组即可得到答案.
19.(1)解:如图所示,⊙O即为所求;
(2)证明:连接OD.
∵OA=OD,
∴∠OAD=∠ODA,
∵AD是∠BAC的角平分线,
∴∠CAD=∠OAD,
∴∠ODA=∠CAD,
∴OD∥AC.
又∵∠C=90°,
∴∠ODB=90°,
∴BC是⊙O的切线.
(1)作AD垂直平分线交AB于点O,点O即为圆心,即可求解;
(2)连接OD,根据等腰三角形的性质得到然后根据角平分线的定义得到,进而可证明即可证明BC为⊙O的切线.
20.(1)解:设h关于的函数解析式为,
将代入解析式,
可得:k=1×20=20,
∴h关于的函数解析式为 .
(2)解:将代入,
可得:,
解得:.
答:该液体的密度为 .
(1)结合题干中的数据,利用待定系数法求出函数解析式即可;
(2)将代入, 再求出即可.
21.(1)69737
(2)解:由图②可知2022年1-2月社会消费品总额为74426亿元.
∵2022年1-2月我国商品零售66708亿元,
∴2022年1-2月我国餐饮收入为
74426-66708=7718(亿元).
∵由图①可知2023年1-2月餐饮收入增长率为9.2%,
∴2023年1-2月我国的餐饮收入为
7718×(1+9.2%)=8428.056≈8428(亿元).
(3)解:2019年1-2月—2020年1-2月我国社会消费品零售总额有所降低,之后几年都在增高.
解:(1)将我国社会消费品零售总额按从小到大的顺序排列为52130,66064,69737,74426,77067,
∴中位数是69737亿元,
故答案为:69737;
(1)根据题意将数据从小到大排列,进而取最中间的数即可得到中位数;
(2)由图②可知2022年1-2月社会消费品总额为74426亿元,进而即可求出2022年1-2月我国餐饮收入,再根据图①即可求解;
(3)根据折线统计图即可求解.
22.(1)解:过点A作AD⊥BC,垂足为D.
(2)解:在RtΔABD中,
在Rt中,
(1)过点A作AD⊥BC,垂足为D,根据题意进行角的运算得到∠ABC的度数;
(2)根据正切函数即可得到BD,进而根据特殊角的三角函数值结合正切函数即可求出CD,再根据BC=BD+CD即可求解。
23.(1)70;95
(2)解:①60;②1.2分或2.8分或4.6分
解:(1)由图像可知,A、B两点之间的距离是70米,
甲机器人前2分钟的速度为:(米/分),
故答案为:70,95;
(2)①∵,乙机器人始终以60米/分钟的速度行走,
∴甲、乙机器人的速度都是60米/分钟;
故答案为:60,
②当时,
解得,,
当时,
,
当时,设甲、乙两机器人之间的距离y米与他们的行走时间x分钟之间函数解析式为,
将点和点代入,得
解得,,
即函数解析式为,
令,得,
,
即两机器人出发1.2分钟,2.8分钟,4.6分钟时相距28米.
(1)找出图象的最高点对应的纵坐标的值即为A、B两点之间的距离,结合图形可得甲机器人前2分钟的路程为(70+60×2)米,然后根据路程÷时间=速度进行解答;
(2)①由图形可得乙机器人始终以60米/分钟的速度行走,据此解答;
②当0≤x≤2时,根据70-甲、乙x分钟的路程差=28建立方程,求解即可;当2
∵,
∴
∴是直角三角形,
和是共边直角三角形;
(2)证明:如图,连接AE,DE,
∵E点是BC中点,
∴AE,DE分别是和斜边上的中线,
∴,∴
∴是等腰三角形,
∵F点是AD中点,∴
(3)解:取BC中点Q,连结AQ,DQ
∵
∴
设
则
∵, ,Q为BC中点,∴
∴
∴
∴
∴∴∴AD平分
(1)由勾股定理求出BC=5,然后根据勾股定理逆定理得到是直角三角形,即可得到答案;
(2)连接AE,DE,根据直角三角形斜边上的中线等于斜边的一半,得,然后根据等腰三角形三线合一的性质即可求解;
(3)取BC中点Q,连结AQ,DQ,由题意得,设,则,, ,推出,由可推出,即可得到答案.
25.存在.当或时,以、、为顶点的三角形与相似
26.解:任务1:如图,作,易证四边形ABFE是矩形,
,
, 斜坡BD的坡比为1:10 ,
,,
,
,
,
,
设抛物线关系式为,
得,解得,
抛物线关系式为,
点D(30,-11),下垂电缆的抛物线的函数表达式为.
任务2:设直线BD的关系式为,
得,解得,
直线BD的关系式为,
设,
,
当时,,
这种电缆的架设不符合安全要求.
任务3:如图,建立直角坐标系,
设,
,
直线BD的关系式为,
,
,
抛物线关系式为,
设,
,
电缆下垂恰好符合安全高度要求,
,解得,
抛物线关系式为,
代入点,得,
解得,
,
两个塔柱的水平距离应为米.
任务1:作,易证四边形ABFE是矩形,利用矩形的性质分别求得各点坐标,再通过待定系数法求得抛物线关系式.
任务2:设直线BD的关系式为,通过待定系数法求得直线BD的关系式,设,用x表示出GH的长度,再利用二次函数的性质求得当时,GH有最小值小于13.5m,故这种电缆的架设不符合安全要求.
任务3:如图,以点B为原点重新建立直角坐标系,设,则,从而得到直线BD的关系式为,及点A、C的坐标,又电缆抛物线的形状与任务1相同,可得抛物线关系式为,设,表示出GH的长度,再利用二次函数的性质求得GH的最小值,进而解得a的值,最后求得两个塔柱的水平距离.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
