2025年中考数学一模猜题卷(江西省专用)—2025年全国各地市最新中考数学模拟考试(含答案)
文档属性
| 名称 | 2025年中考数学一模猜题卷(江西省专用)—2025年全国各地市最新中考数学模拟考试(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 20:58:54 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
机密★启用前 姓名___________ 准考证号____________
2025 年 江 西 省 中 考 一 模 猜 题 卷
数 学
说明: 1. 本试卷满分] 20 分, 考试时间1 分钟。
2 、请试序号在答题卡相应位置作答答在试题卷或其它位置无效。
一、单项选择题(本大题共6小题,每小题3分,共18分)在每小题列出的四个备选项中只有一项是最符合题目要求的,请将其代码填涂在答题卡相应位置.错选、多选或未选均不得分.
1.的相反数是( )
A.7 B.﹣7 C.- D.
2.我国2024年春节档电影票房达80.16亿元,创造了新的春节档票房纪录,其中数据80.16亿用科学记数法表示为( )
A.80.16x108 B.8.016x109 C.0.8016x1010 D.80.16x1010
3.《清朝野史大观 清代述异》称:"中国讲求熟茶,以闽之汀、漳、泉三府,粵之潮州府功夫茶为最。"如图是喝功夫茶的一个茶杯,关于该茶杯的三视图,下列说法正确的是( )
A.主视图与左视图相同 B.主视图与俯视图相同
C.左视图与俯视图相同 D.三视图都相同
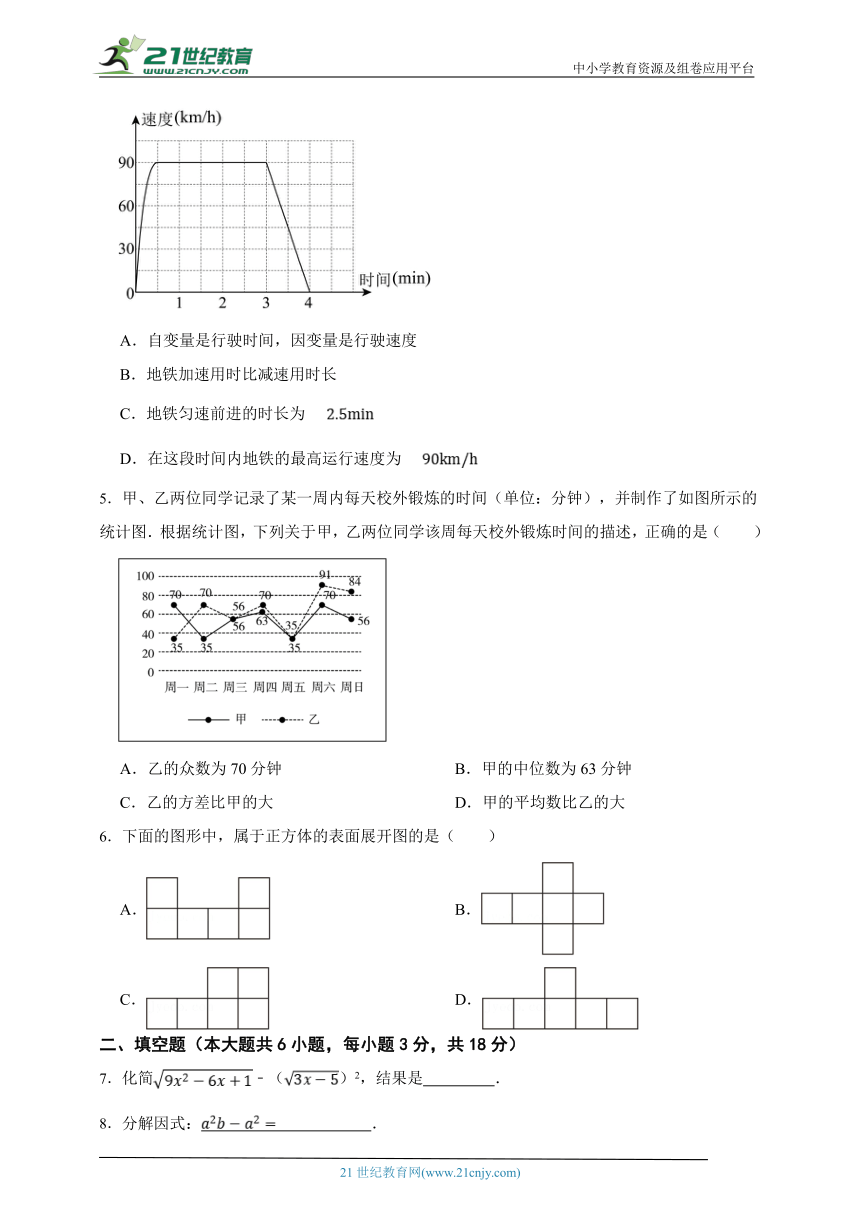
4.深圳地铁号线,也称“深圳地铁东部快线”,它起于福田区岗厦北交通枢纽,途至坪山区沙田,采用自动化无人驾驶技术,全长,最高运行速度可达.如图,为地铁号线从黄木岗站到罗湖北站行驶的速度时间图象,根据图象,下列分析错误的是( )
A.自变量是行驶时间,因变量是行驶速度
B.地铁加速用时比减速用时长
C.地铁匀速前进的时长为
D.在这段时间内地铁的最高运行速度为
5.甲、乙两位同学记录了某一周内每天校外锻炼的时间(单位:分钟),并制作了如图所示的统计图.根据统计图,下列关于甲,乙两位同学该周每天校外锻炼时间的描述,正确的是( )
A.乙的众数为70分钟 B.甲的中位数为63分钟
C.乙的方差比甲的大 D.甲的平均数比乙的大
6.下面的图形中,属于正方体的表面展开图的是( )
A. B.
C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
7.化简﹣()2,结果是 .
8.分解因式: .
9.在探究“反比例函数的图象与性质”时,小明先将直角边长为5个单位长度的等腰直角三角板ABC摆放在平面直角坐标系中,使其两条直角边AC,BC分别落在x轴负半轴、y轴正半轴上(如图所示),然后将三角板向右平移a个单位长度,再向下平移a个单位长度后,小明发现A,B两点恰好都落在函数的图象上,则a的值为 .
10.一个容器装有1L水,按照如下要求把水倒出:第1次倒出水,第2次倒出的水量是的,第3次倒出的水量是的,第4次倒出的水量是的……,则第n次倒出后,倒出的水的总量为 L.
11. 如图,的面积为4,点P在对角线上,E、F分别在、上,且,,连接,图中阴影部分的面积为 .
12.如图示,半圆的直径,弦,将半圆沿着过点A的直线折叠,折叠后使得弦恰好落在直径上,则折痕的长为 .
三、解答题(本大题共5小题,每小题6分,共30分)
13.(1)计算:;
化简:.
14.如图,四边形ABCD的对角线AC,BD相交于点O,AO=CO,EF过点O且与AD, BC分别相交于点E,F,OE=OF.
(1)求证:四边形ABCD是平行四边形;
(2)连结AF,若EF⊥AC,△ABF的周长是15 ,求四边形ABCD的周长.
15.一只不透明的袋子里共有个球,其中个白球,个红球,它们除颜色外均相同.
(1)从袋子中随机摸出一个球是白球的概率是多少?
(2)从袋子中随机摸出一个球,不放回袋子,摇匀袋子后再摸一个球,请用列表或画树状图的方法,求出两次摸出的球都是白球的概率.
16.如图,一次函数y1=mx+n(m≠0)的图象与反比例函数y2=(k≠0)的图象相交于A(a,-1),B(-1,3)两点,且一次函数的图象交x轴于点C,交y轴于点D.
(1)求一次函数和反比例函数的表达式.
(2)第四象限的反比例图象上有一点P,使得S△OCP=4S△OBD,请求出点P的坐标.
(3)对于反比例函数y2=(k≠0),当y≤3时,直接写出x的取值范围.
17.如图,在中,,,以为直径的与相交于点,为上一点,且.
(1)求的长;
(2)若,求证:为的切线.
四、解答题(本大题共3小题,每小题8分,共24分)
18.遵义茶历史悠久,早从夜郎古国的茶马古道开始,遵义茶便从崇山峻岭中走出来,某茶叶店准备购买湄潭翠芽和湄江翠片两种茶叶进行销售,已知购买4千克湄潭翠芽和3千克湄江翠片需要2500元;购买2千克湄潭翠芽和5千克湄江翠片需要2300元.
(1)求湄潭翠芽、湄江翠片两种茶叶的单价分别为多少?
(2)该茶叶店计划购买湄潭翠芽、湄江翠片两种茶叶共80千克,总费用不超过26000元,并且要求湄潭翠芽数量不能低于10千克,最少费用为多少元?
19.如图, 在 中, 为线段 的中点, 延长 交 的延长线于点 , 连结 .
(1)求证: 四边形 是矩形.
(2) 连结 , 若 , 求 的长.
20.在中,是的中线,AE是的平分线,交AE的延长线于.
(1)若,求的度数;
(2)求证:是等腰三角形.
五、解答题(本大题共2小题,每小题9分,共18分)
21.某中学随机抽取了一部分九年级女同学进行1分钟跳绳抽测,将测得的成绩绘制成如下的频数表及统计图:
跳绳抽测成绩的频数
级别 成绩(次) 频数
A 130B 140C 150D 160E 170跳绳级别扇形统计图
请回答下列问题:
(1)本次抽取了 人;
(2)请补全E组频数为 .
(3)若规定D,E两个级别的成绩为“优秀”,全校七年级女生共有200名,请估计该校跳绳优秀的七年级女生人数.
22.如图,从地面竖直向上抛出一小球,小球的高度单位:与小球的运动时间单位:之间的关系式是.
(1)当小球运动的时间是多少时,小球回落到地面处?
(2)求小球在运动过程中的最大高度.
六、解答题(本大题共12分)
23.【问题情境】
在综合实践活动课上,李老师让同桌两位同学用相同的两块含的三角板开展数学探究活动.两块三角板分别记作和,设AB.
【操作探究】
如图(1),先将和的边重合,再将绕着点按顺时针方向旋转,旋转角为,旋转过程中保持不动,连接BC.
(1)当时, ;当时,
(2)当时,画出图形,并求两块三角板重叠部分图形的面积;
(3)如图(2),取BC的中点,将绕着点旋转一周,点的运动路径长为 .
答案解析部分
1.C
解:的相反数是-.
故答案为:C.
0的相反数是0,只有符号不同的两个数互为相反数。根据相反数的定义作答即可。
2.B
解:
故答案为:B.
根据科学记数法的通常形式为,其中 是一个不小于1但小于10的实数, 是一个整数.
3.A
解:这个茶杯的主视图与左视图相同,俯视图与主视图和左视图不相同.
故答案为:A.
掌握三视图的概念是解题关键.
4.B
解:A、由图像可知:自变量是行驶时间,因变量是行驶速度,选项正确,不符合题意;
B、地铁加速时间是从0min到0.5min用时0.5min,减速时间是3min到4min用时1min,故地铁加速用时比减速用时短,选项错误,符合题意;
C、地铁匀速前进是从0.5min到3min这一段时间,时长3-0.5=2.5min,选项正确,不符合题意;
D、这段时间内因变量最大值为90km/h,故地铁的最高运行速度为90km/h,选项正确,不符合题意;
故答案为:B.
本题考查运用图象表示时间与速度之间的关系,通过图象进行判断;同时要注意题干提问方式,本题是要求选出错误选项.
5.C
6.B
解:正方体的表面展开图有141型,222型,132型,B符合141型,
故答案为:B.
结合立体图形和平面展开图的关系作答即可.
7.4
8.
解:a2b-a2=a2(b-1).
故答案为:a2(b-1).
把公因式a2提出来,将多项式化成两个因式乘积的形式即可.
9.2或3
解:设平移后点A,B对应的点为C,D,
根据题意,得OA=OB=5,
∴A(-5,0),B(0,5),
∴C(-5+a,-a),D(a,5-a),
∵C,D在函数的图象上,
∴-a(-5+a)=6
解得:a1=2,a2=3,
故答案为:2或3.
设平移后点A,B对应的点为C,D,根据题意得A,B的坐标,然后利用坐标的平移规律得点C,D的坐标,接下来根据反比例函数上点的坐标特征得关于a的方程,解方程求出a的值即可.
10.
解:第1次倒出升水,
第2次倒出水量是升的,
第3次倒出水量是升的,
第4次倒出水量是升的,
…,
第n次倒出水量是升的,
则第n次倒出水后,倒出的水量为:
;
故答案为:.
根据题目信息可推得第n次倒出水量是升的,将前n次倒出的水量相加即可求解.
11.2
解:如图,
∵平行四边形ABCD,
∴AD∥BC,AB∥DC,
∵PE∥BC,PF∥CD,
∴AE∥PF,AF∥PE,
∴四边形AEPF是平行四边形,
易证△AOE≌△POF(SAS),
∴S△AOE≌S△POF,
∴S阴影部分=S△ACD=S平行四边形ABCD=×4=2.
故答案为:2.
利用平行四边形的性质可证AD∥BC,AB∥DC,可推出AE∥PF,AF∥PE,利用有两组对边分别平行的四边形是平行四边形,可证得四边形AEPF是平行四边形,利用SAS可证得△AOE≌△POF,可得到S△AOE≌S△POF,由此可证得S阴影部分=S△ACD=S平行四边形ABCD,据此可求出阴影部分的面积.
12.
13.(1)解:原式=1+5
=6;
(2)解:原式==1.
14.(1)证明∵AO=CO,∠AOE=∠COF,OE=OF,
∴△AOE≌△COF(SAS),
∴∠OAE=∠OCF,
∵AD∥BC,∴∠EDO= ∠FBO.
又∵OE=OF,∠EOD= ∠FOB,
∴△EOD≌△FOB(AAS),
∴OD=OB.
∵OA=OC,∴四边形ABCD是平行四边形.
(2)解:∵EF⊥AC,AO=CO,
∴AF=FC,
∴AB+BF+AF=AB+BF+FC=15,
即AB+BC=15,
∴ABCD的周长= 2(AB+BC)= 2×15=30.
(1)由可证,可得,由可证,可得,根据对角线互相平分的四边形是平行四边形,即可证明四边形是平行四边形;
(2)由线段中垂线的性质可得,可得,即可求四边形的周长.
15.(1)解:∵不透明的袋子里共有个球,其中个白球,个红球,
∴摸出一个球是白球;
(2)解:画树形图如下:
共有12种等可能的结果,其中两次摸出的球是白球的有6种,
∴两次摸出的求都是白球.
(1)根据摸出一个球是白球即可求解;
(2)先根据题意画出树状图,进而即可得到 共有12种等可能的结果,其中两次摸出的球是白球的有6种, 再运用等可能事件的概率结合题意即可求解。
16.(1)解:反比例函数的图象过点,
∴,
∴,
∵在双曲线上.
∴,
∴,
∴,
∵一次函数的图象经过、,
∴,解得,
∴一次函数的解析式为;
(2)解:在中,当时,;当时,则,
∴,,
∴,
∴,
∵,
∴,即,
∴,
∵点P在第四象限,
∴,
代入得,,
解得,
∴点P的坐标为;
(3)解:观察图象可知,对于反比例函数,当时,x的取值范围是或.
【分式】(1)利用待定系数法求得,进而得,然后利用待定系数法即可求得一次函数的解析式;
(2)由直线解析式求得,,进而求得,由题意得到,即,即可求得点P的坐标为;
(3)通过图象观察就可以直接看出当时的取值范围.
17.(1)解:如图,连接,
,
,
,
,
半径长是3,
的长;
答:的长为.
(2)证明:
,
,
,
,
直径,
为的切线.
(1)根据圆周角的性质可得,从而可求出,半径为3,在由弧长公式“”即可求出的度;
(2)由圆周角的性质得出,从而求出,再由三角形的内角和定理得出∠ABC=90°,即可说明为的切线.
18.(1)解:设湄潭翠芽的单价为x元,湄江翠片的单价为y元,根据题意可知,
,
即,
答:湄潭翠芽的单价为400元,湄江翠片的单价为300元;
(2)解:设购买湄潭翠芽m千克,则湄江翠片购买了(80-m)千克,总费用为w元,
根据题意可知,400m+300(80-m)≤26000,
即m≤20,
∵湄潭翠芽数量不能低于10千克,
∴m的取值范围为10≤m≤20,
∴w=400m+(80-m)=100m+24000,
∵100>0,
∴w随m的增大而增大,
∴当m=10时,w最小,最小值为25000,
∴最少费用为25000元.
(1)设湄潭翠芽的单价为x元,湄江翠片的单价为y元,根据题意列出方程组,解方程组即可得到答案;
(2)设购买湄潭翠芽m千克,则湄江翠片购买了(80-m)千克,总费用为w元,根据题意列出不等式,求出m的取值范围为10≤m≤20,再列出w关于m的关系式,求出w的最小值即可得到答案.
19.(1)证明: ∵O是线段 AD 的中点,
∴OA=OD.
四边形 是平行四边形,
即
,
四边形 是平行四边形.
,
,
平行四边形 是矩形
(2)如图,过点O作OF⊥DE,垂足为F,如图所示,
在矩形ABDE中,AB=DE=2,
,
,
,
,
∴OF 为 的中位线,
.
四边形 是平行四边形,
在 Rt 中, 由勾股定理得,
即 的长为
(1)根据平行四边形的性质准备条件,根据ASA证明△AOB和△DOE全等,得AB=DE,再根据平行四边形的判定和矩形的判定证明即可;
(2)根据矩形的性质和直角三角形斜边中线的性质求出OF的长,根据平行四边形的性质求出CF的长,根据勾股定理求出OC的长。
20.(1)解:∵AB=AC,AD是△ABC的中线
∴∠BAD=∠BAC=60°;
(2)证明:∵AE是∠BAD的平分线
∴∠BAF=∠DAF
∵AB∥DF
∴∠BAF=∠AFD
∴∠DAF=∠AFD
∴△ADF是等腰三角形
(1)根据等腰三角形的三线合一直接求解即可;
(2)根据角平分线的定义得∠BAF=∠DAF,根据二直线平行,内错角相等,得∠BAF=∠AFD,则∠DAF=∠AFD,从而根据有两个角相等的三角形就是等腰三角形可得结论.
21.(1)40
(2)5
(3)解: (人)
故该校跳绳成绩优秀的女同学人数大概为85人.
解:(1)7÷17.5%=40(人)
故答案为:40.
(2)40-2-7-14-12=5(人)
故答案为:5.
补全频数表如图:
级别 成绩(次) 频数
A 130B 140C 150D 160E 170(1)用B组人数÷所占百分比即可得到总人数;
(2)用总人数减其他已知的各组频数,即可得到E组的频数,再补全频数表即可;
(3)用200ד优秀”的人数的占比,即可估计估算出全校的优秀女生人数.
22.(1)解:当时,,
解得或,
答:当小球运动的时间是时,小球回落到地面处;
(2)解:,
当时,最大.
答:小球在运动过程中的最大高度为.
(1)将h=0代入关系式,解方程即可求出答案.
(2)将关系式转换为顶点式,再根据二次函数的性质即可求出答案.
23.(1)2;30或210
(2)解:当时,如图(1),
设分别与BD,AB交于点E,F,AC与BD交于点,
∴四边形AGEF为两块三角板重叠部分的面积,
∵∠D'=∠DAD'=∠D=90°,
∴四边形是正方形,
∴AD=AD',
,
∴,
,
,
∴∠DAG=30°,
∴,
∴,
,
∴∠BEF=∠D'FA=60°,
∴,
∴,
;
(3)2π
解:(1)如图,
∵∠ABD=∠A'CD'=30°,∠ADC=∠A'D'C=90°,
∴∠BAD=∠D'A'C=60°,
∴当α=60°时,点D'在AB上,A、D、C三点共线,
∵AB=AC,
∴是等边三角形,
∴BC=AB,
∵AB=2,
∴BC=2,
如图,过点A作AE⊥BC于点E,
∴∠AEB=∠AEC=90°,
∵AB=AC=2,,
∴,
在中,根据勾股定理得,,
∴AE=BE=CE,
∴∠BAE=∠CAE=45°,
∴∠BAC=90°,
∴α=60°+60°-90°=30°,
如图,
同理可得∠BAC=90°,
∴α=60°+60°+90°=210°,
综上所述,当时,α=30°或210°,
故答案为:2,30或120;
(3)如图,连接AF,
∵AB=AC,F为BC中点,
∴AF⊥BC,
∴∠AFB=90°,
∴点F的运动轨迹为以AB为直径的圆,
∵AB=2,
∴点F的运动路径长为2π,
故答案为:2π.
(1)当α=60°时,点D'在AB上,A、D、C三点共线,根据等边三角形的判定得是等边三角形,从而有BC=AB=2;分类讨论画出图形,过点A作AE⊥BC于E,根据等腰三角形”三线合一“性质得BE=CE,利用勾股定理求出AE的长,从而得AE=BE=CE,得∠BAE=∠CAE=45°,进而得∠BAC=90°,最后即可求出α=30°或210°;
(2)设分别与BD,AB交于点E,F,AC与BD交于点,易证四边形是正方形,得AD=AD',接下来利用含30°的直角三角形的性质求出AD=AD'=1,从而得正方形的面积为1,利用三角形内角和定理求出∠DAG=30°,然后利用特殊角的三角函数值解直角三角形,得DG的长,利用三角形面积公式得三角形ADG的面积,接下来求∠BEF=∠D'FA=60°,利用特殊角的三角函数值解直角三角形得D'F的值,利用三角形面积公式得三角形AD'F的面积,最后用正方形面积减去两个三角形的面积即可;
(3)连接AF,利用等腰三角形"三线合一”性质得AF⊥BC,得∠AFB=90°,可知点F的运动为“定角定弦”隐圆问题,从而得出点F的轨迹是以AB为直径的圆,最后利用圆的周长公式求出点F的运动路径长.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
机密★启用前 姓名___________ 准考证号____________
2025 年 江 西 省 中 考 一 模 猜 题 卷
数 学
说明: 1. 本试卷满分] 20 分, 考试时间1 分钟。
2 、请试序号在答题卡相应位置作答答在试题卷或其它位置无效。
一、单项选择题(本大题共6小题,每小题3分,共18分)在每小题列出的四个备选项中只有一项是最符合题目要求的,请将其代码填涂在答题卡相应位置.错选、多选或未选均不得分.
1.的相反数是( )
A.7 B.﹣7 C.- D.
2.我国2024年春节档电影票房达80.16亿元,创造了新的春节档票房纪录,其中数据80.16亿用科学记数法表示为( )
A.80.16x108 B.8.016x109 C.0.8016x1010 D.80.16x1010
3.《清朝野史大观 清代述异》称:"中国讲求熟茶,以闽之汀、漳、泉三府,粵之潮州府功夫茶为最。"如图是喝功夫茶的一个茶杯,关于该茶杯的三视图,下列说法正确的是( )
A.主视图与左视图相同 B.主视图与俯视图相同
C.左视图与俯视图相同 D.三视图都相同
4.深圳地铁号线,也称“深圳地铁东部快线”,它起于福田区岗厦北交通枢纽,途至坪山区沙田,采用自动化无人驾驶技术,全长,最高运行速度可达.如图,为地铁号线从黄木岗站到罗湖北站行驶的速度时间图象,根据图象,下列分析错误的是( )
A.自变量是行驶时间,因变量是行驶速度
B.地铁加速用时比减速用时长
C.地铁匀速前进的时长为
D.在这段时间内地铁的最高运行速度为
5.甲、乙两位同学记录了某一周内每天校外锻炼的时间(单位:分钟),并制作了如图所示的统计图.根据统计图,下列关于甲,乙两位同学该周每天校外锻炼时间的描述,正确的是( )
A.乙的众数为70分钟 B.甲的中位数为63分钟
C.乙的方差比甲的大 D.甲的平均数比乙的大
6.下面的图形中,属于正方体的表面展开图的是( )
A. B.
C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
7.化简﹣()2,结果是 .
8.分解因式: .
9.在探究“反比例函数的图象与性质”时,小明先将直角边长为5个单位长度的等腰直角三角板ABC摆放在平面直角坐标系中,使其两条直角边AC,BC分别落在x轴负半轴、y轴正半轴上(如图所示),然后将三角板向右平移a个单位长度,再向下平移a个单位长度后,小明发现A,B两点恰好都落在函数的图象上,则a的值为 .
10.一个容器装有1L水,按照如下要求把水倒出:第1次倒出水,第2次倒出的水量是的,第3次倒出的水量是的,第4次倒出的水量是的……,则第n次倒出后,倒出的水的总量为 L.
11. 如图,的面积为4,点P在对角线上,E、F分别在、上,且,,连接,图中阴影部分的面积为 .
12.如图示,半圆的直径,弦,将半圆沿着过点A的直线折叠,折叠后使得弦恰好落在直径上,则折痕的长为 .
三、解答题(本大题共5小题,每小题6分,共30分)
13.(1)计算:;
化简:.
14.如图,四边形ABCD的对角线AC,BD相交于点O,AO=CO,EF过点O且与AD, BC分别相交于点E,F,OE=OF.
(1)求证:四边形ABCD是平行四边形;
(2)连结AF,若EF⊥AC,△ABF的周长是15 ,求四边形ABCD的周长.
15.一只不透明的袋子里共有个球,其中个白球,个红球,它们除颜色外均相同.
(1)从袋子中随机摸出一个球是白球的概率是多少?
(2)从袋子中随机摸出一个球,不放回袋子,摇匀袋子后再摸一个球,请用列表或画树状图的方法,求出两次摸出的球都是白球的概率.
16.如图,一次函数y1=mx+n(m≠0)的图象与反比例函数y2=(k≠0)的图象相交于A(a,-1),B(-1,3)两点,且一次函数的图象交x轴于点C,交y轴于点D.
(1)求一次函数和反比例函数的表达式.
(2)第四象限的反比例图象上有一点P,使得S△OCP=4S△OBD,请求出点P的坐标.
(3)对于反比例函数y2=(k≠0),当y≤3时,直接写出x的取值范围.
17.如图,在中,,,以为直径的与相交于点,为上一点,且.
(1)求的长;
(2)若,求证:为的切线.
四、解答题(本大题共3小题,每小题8分,共24分)
18.遵义茶历史悠久,早从夜郎古国的茶马古道开始,遵义茶便从崇山峻岭中走出来,某茶叶店准备购买湄潭翠芽和湄江翠片两种茶叶进行销售,已知购买4千克湄潭翠芽和3千克湄江翠片需要2500元;购买2千克湄潭翠芽和5千克湄江翠片需要2300元.
(1)求湄潭翠芽、湄江翠片两种茶叶的单价分别为多少?
(2)该茶叶店计划购买湄潭翠芽、湄江翠片两种茶叶共80千克,总费用不超过26000元,并且要求湄潭翠芽数量不能低于10千克,最少费用为多少元?
19.如图, 在 中, 为线段 的中点, 延长 交 的延长线于点 , 连结 .
(1)求证: 四边形 是矩形.
(2) 连结 , 若 , 求 的长.
20.在中,是的中线,AE是的平分线,交AE的延长线于.
(1)若,求的度数;
(2)求证:是等腰三角形.
五、解答题(本大题共2小题,每小题9分,共18分)
21.某中学随机抽取了一部分九年级女同学进行1分钟跳绳抽测,将测得的成绩绘制成如下的频数表及统计图:
跳绳抽测成绩的频数
级别 成绩(次) 频数
A 130
请回答下列问题:
(1)本次抽取了 人;
(2)请补全E组频数为 .
(3)若规定D,E两个级别的成绩为“优秀”,全校七年级女生共有200名,请估计该校跳绳优秀的七年级女生人数.
22.如图,从地面竖直向上抛出一小球,小球的高度单位:与小球的运动时间单位:之间的关系式是.
(1)当小球运动的时间是多少时,小球回落到地面处?
(2)求小球在运动过程中的最大高度.
六、解答题(本大题共12分)
23.【问题情境】
在综合实践活动课上,李老师让同桌两位同学用相同的两块含的三角板开展数学探究活动.两块三角板分别记作和,设AB.
【操作探究】
如图(1),先将和的边重合,再将绕着点按顺时针方向旋转,旋转角为,旋转过程中保持不动,连接BC.
(1)当时, ;当时,
(2)当时,画出图形,并求两块三角板重叠部分图形的面积;
(3)如图(2),取BC的中点,将绕着点旋转一周,点的运动路径长为 .
答案解析部分
1.C
解:的相反数是-.
故答案为:C.
0的相反数是0,只有符号不同的两个数互为相反数。根据相反数的定义作答即可。
2.B
解:
故答案为:B.
根据科学记数法的通常形式为,其中 是一个不小于1但小于10的实数, 是一个整数.
3.A
解:这个茶杯的主视图与左视图相同,俯视图与主视图和左视图不相同.
故答案为:A.
掌握三视图的概念是解题关键.
4.B
解:A、由图像可知:自变量是行驶时间,因变量是行驶速度,选项正确,不符合题意;
B、地铁加速时间是从0min到0.5min用时0.5min,减速时间是3min到4min用时1min,故地铁加速用时比减速用时短,选项错误,符合题意;
C、地铁匀速前进是从0.5min到3min这一段时间,时长3-0.5=2.5min,选项正确,不符合题意;
D、这段时间内因变量最大值为90km/h,故地铁的最高运行速度为90km/h,选项正确,不符合题意;
故答案为:B.
本题考查运用图象表示时间与速度之间的关系,通过图象进行判断;同时要注意题干提问方式,本题是要求选出错误选项.
5.C
6.B
解:正方体的表面展开图有141型,222型,132型,B符合141型,
故答案为:B.
结合立体图形和平面展开图的关系作答即可.
7.4
8.
解:a2b-a2=a2(b-1).
故答案为:a2(b-1).
把公因式a2提出来,将多项式化成两个因式乘积的形式即可.
9.2或3
解:设平移后点A,B对应的点为C,D,
根据题意,得OA=OB=5,
∴A(-5,0),B(0,5),
∴C(-5+a,-a),D(a,5-a),
∵C,D在函数的图象上,
∴-a(-5+a)=6
解得:a1=2,a2=3,
故答案为:2或3.
设平移后点A,B对应的点为C,D,根据题意得A,B的坐标,然后利用坐标的平移规律得点C,D的坐标,接下来根据反比例函数上点的坐标特征得关于a的方程,解方程求出a的值即可.
10.
解:第1次倒出升水,
第2次倒出水量是升的,
第3次倒出水量是升的,
第4次倒出水量是升的,
…,
第n次倒出水量是升的,
则第n次倒出水后,倒出的水量为:
;
故答案为:.
根据题目信息可推得第n次倒出水量是升的,将前n次倒出的水量相加即可求解.
11.2
解:如图,
∵平行四边形ABCD,
∴AD∥BC,AB∥DC,
∵PE∥BC,PF∥CD,
∴AE∥PF,AF∥PE,
∴四边形AEPF是平行四边形,
易证△AOE≌△POF(SAS),
∴S△AOE≌S△POF,
∴S阴影部分=S△ACD=S平行四边形ABCD=×4=2.
故答案为:2.
利用平行四边形的性质可证AD∥BC,AB∥DC,可推出AE∥PF,AF∥PE,利用有两组对边分别平行的四边形是平行四边形,可证得四边形AEPF是平行四边形,利用SAS可证得△AOE≌△POF,可得到S△AOE≌S△POF,由此可证得S阴影部分=S△ACD=S平行四边形ABCD,据此可求出阴影部分的面积.
12.
13.(1)解:原式=1+5
=6;
(2)解:原式==1.
14.(1)证明∵AO=CO,∠AOE=∠COF,OE=OF,
∴△AOE≌△COF(SAS),
∴∠OAE=∠OCF,
∵AD∥BC,∴∠EDO= ∠FBO.
又∵OE=OF,∠EOD= ∠FOB,
∴△EOD≌△FOB(AAS),
∴OD=OB.
∵OA=OC,∴四边形ABCD是平行四边形.
(2)解:∵EF⊥AC,AO=CO,
∴AF=FC,
∴AB+BF+AF=AB+BF+FC=15,
即AB+BC=15,
∴ABCD的周长= 2(AB+BC)= 2×15=30.
(1)由可证,可得,由可证,可得,根据对角线互相平分的四边形是平行四边形,即可证明四边形是平行四边形;
(2)由线段中垂线的性质可得,可得,即可求四边形的周长.
15.(1)解:∵不透明的袋子里共有个球,其中个白球,个红球,
∴摸出一个球是白球;
(2)解:画树形图如下:
共有12种等可能的结果,其中两次摸出的球是白球的有6种,
∴两次摸出的求都是白球.
(1)根据摸出一个球是白球即可求解;
(2)先根据题意画出树状图,进而即可得到 共有12种等可能的结果,其中两次摸出的球是白球的有6种, 再运用等可能事件的概率结合题意即可求解。
16.(1)解:反比例函数的图象过点,
∴,
∴,
∵在双曲线上.
∴,
∴,
∴,
∵一次函数的图象经过、,
∴,解得,
∴一次函数的解析式为;
(2)解:在中,当时,;当时,则,
∴,,
∴,
∴,
∵,
∴,即,
∴,
∵点P在第四象限,
∴,
代入得,,
解得,
∴点P的坐标为;
(3)解:观察图象可知,对于反比例函数,当时,x的取值范围是或.
【分式】(1)利用待定系数法求得,进而得,然后利用待定系数法即可求得一次函数的解析式;
(2)由直线解析式求得,,进而求得,由题意得到,即,即可求得点P的坐标为;
(3)通过图象观察就可以直接看出当时的取值范围.
17.(1)解:如图,连接,
,
,
,
,
半径长是3,
的长;
答:的长为.
(2)证明:
,
,
,
,
直径,
为的切线.
(1)根据圆周角的性质可得,从而可求出,半径为3,在由弧长公式“”即可求出的度;
(2)由圆周角的性质得出,从而求出,再由三角形的内角和定理得出∠ABC=90°,即可说明为的切线.
18.(1)解:设湄潭翠芽的单价为x元,湄江翠片的单价为y元,根据题意可知,
,
即,
答:湄潭翠芽的单价为400元,湄江翠片的单价为300元;
(2)解:设购买湄潭翠芽m千克,则湄江翠片购买了(80-m)千克,总费用为w元,
根据题意可知,400m+300(80-m)≤26000,
即m≤20,
∵湄潭翠芽数量不能低于10千克,
∴m的取值范围为10≤m≤20,
∴w=400m+(80-m)=100m+24000,
∵100>0,
∴w随m的增大而增大,
∴当m=10时,w最小,最小值为25000,
∴最少费用为25000元.
(1)设湄潭翠芽的单价为x元,湄江翠片的单价为y元,根据题意列出方程组,解方程组即可得到答案;
(2)设购买湄潭翠芽m千克,则湄江翠片购买了(80-m)千克,总费用为w元,根据题意列出不等式,求出m的取值范围为10≤m≤20,再列出w关于m的关系式,求出w的最小值即可得到答案.
19.(1)证明: ∵O是线段 AD 的中点,
∴OA=OD.
四边形 是平行四边形,
即
,
四边形 是平行四边形.
,
,
平行四边形 是矩形
(2)如图,过点O作OF⊥DE,垂足为F,如图所示,
在矩形ABDE中,AB=DE=2,
,
,
,
,
∴OF 为 的中位线,
.
四边形 是平行四边形,
在 Rt 中, 由勾股定理得,
即 的长为
(1)根据平行四边形的性质准备条件,根据ASA证明△AOB和△DOE全等,得AB=DE,再根据平行四边形的判定和矩形的判定证明即可;
(2)根据矩形的性质和直角三角形斜边中线的性质求出OF的长,根据平行四边形的性质求出CF的长,根据勾股定理求出OC的长。
20.(1)解:∵AB=AC,AD是△ABC的中线
∴∠BAD=∠BAC=60°;
(2)证明:∵AE是∠BAD的平分线
∴∠BAF=∠DAF
∵AB∥DF
∴∠BAF=∠AFD
∴∠DAF=∠AFD
∴△ADF是等腰三角形
(1)根据等腰三角形的三线合一直接求解即可;
(2)根据角平分线的定义得∠BAF=∠DAF,根据二直线平行,内错角相等,得∠BAF=∠AFD,则∠DAF=∠AFD,从而根据有两个角相等的三角形就是等腰三角形可得结论.
21.(1)40
(2)5
(3)解: (人)
故该校跳绳成绩优秀的女同学人数大概为85人.
解:(1)7÷17.5%=40(人)
故答案为:40.
(2)40-2-7-14-12=5(人)
故答案为:5.
补全频数表如图:
级别 成绩(次) 频数
A 130
(2)用总人数减其他已知的各组频数,即可得到E组的频数,再补全频数表即可;
(3)用200ד优秀”的人数的占比,即可估计估算出全校的优秀女生人数.
22.(1)解:当时,,
解得或,
答:当小球运动的时间是时,小球回落到地面处;
(2)解:,
当时,最大.
答:小球在运动过程中的最大高度为.
(1)将h=0代入关系式,解方程即可求出答案.
(2)将关系式转换为顶点式,再根据二次函数的性质即可求出答案.
23.(1)2;30或210
(2)解:当时,如图(1),
设分别与BD,AB交于点E,F,AC与BD交于点,
∴四边形AGEF为两块三角板重叠部分的面积,
∵∠D'=∠DAD'=∠D=90°,
∴四边形是正方形,
∴AD=AD',
,
∴,
,
,
∴∠DAG=30°,
∴,
∴,
,
∴∠BEF=∠D'FA=60°,
∴,
∴,
;
(3)2π
解:(1)如图,
∵∠ABD=∠A'CD'=30°,∠ADC=∠A'D'C=90°,
∴∠BAD=∠D'A'C=60°,
∴当α=60°时,点D'在AB上,A、D、C三点共线,
∵AB=AC,
∴是等边三角形,
∴BC=AB,
∵AB=2,
∴BC=2,
如图,过点A作AE⊥BC于点E,
∴∠AEB=∠AEC=90°,
∵AB=AC=2,,
∴,
在中,根据勾股定理得,,
∴AE=BE=CE,
∴∠BAE=∠CAE=45°,
∴∠BAC=90°,
∴α=60°+60°-90°=30°,
如图,
同理可得∠BAC=90°,
∴α=60°+60°+90°=210°,
综上所述,当时,α=30°或210°,
故答案为:2,30或120;
(3)如图,连接AF,
∵AB=AC,F为BC中点,
∴AF⊥BC,
∴∠AFB=90°,
∴点F的运动轨迹为以AB为直径的圆,
∵AB=2,
∴点F的运动路径长为2π,
故答案为:2π.
(1)当α=60°时,点D'在AB上,A、D、C三点共线,根据等边三角形的判定得是等边三角形,从而有BC=AB=2;分类讨论画出图形,过点A作AE⊥BC于E,根据等腰三角形”三线合一“性质得BE=CE,利用勾股定理求出AE的长,从而得AE=BE=CE,得∠BAE=∠CAE=45°,进而得∠BAC=90°,最后即可求出α=30°或210°;
(2)设分别与BD,AB交于点E,F,AC与BD交于点,易证四边形是正方形,得AD=AD',接下来利用含30°的直角三角形的性质求出AD=AD'=1,从而得正方形的面积为1,利用三角形内角和定理求出∠DAG=30°,然后利用特殊角的三角函数值解直角三角形,得DG的长,利用三角形面积公式得三角形ADG的面积,接下来求∠BEF=∠D'FA=60°,利用特殊角的三角函数值解直角三角形得D'F的值,利用三角形面积公式得三角形AD'F的面积,最后用正方形面积减去两个三角形的面积即可;
(3)连接AF,利用等腰三角形"三线合一”性质得AF⊥BC,得∠AFB=90°,可知点F的运动为“定角定弦”隐圆问题,从而得出点F的轨迹是以AB为直径的圆,最后利用圆的周长公式求出点F的运动路径长.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
