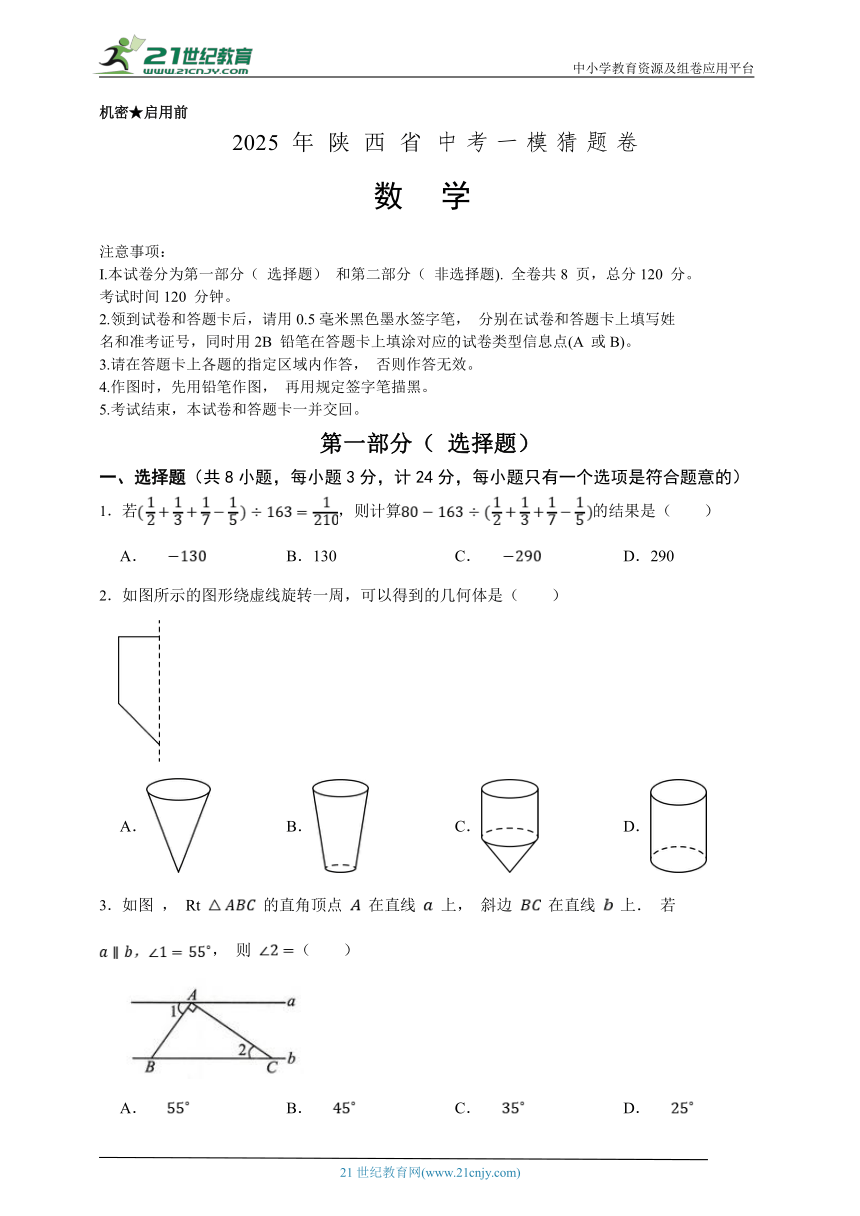
2025年中考数学一模猜题卷(陕西省专用)—2025年全国各地市最新中考数学模拟考试(含答案)
文档属性
| 名称 | 2025年中考数学一模猜题卷(陕西省专用)—2025年全国各地市最新中考数学模拟考试(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 00:00:00 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
机密★启用前
2025 年 陕 西 省 中 考 一 模 猜 题 卷
数 学
注意事项:
I.本试卷分为第一部分( 选择题) 和第二部分( 非选择题). 全卷共8 页,总分120 分。
考试时间120 分钟。
2.领到试卷和答题卡后,请用0.5毫米黑色墨水签字笔, 分别在试卷和答题卡上填写姓
名和准考证号,同时用2B 铅笔在答题卡上填涂对应的试卷类型信息点(A 或B)。
3.请在答題卡上各题的指定区域内作答, 否则作答无效。
4.作图时,先用铅笔作图, 再用规定签字笔描黑。
5.考试结束,本试卷和答题卡一并交回。
第一部分( 选择题)
一、选择题(共8小题,每小题3分,计24分,每小题只有一个选项是符合题意的)
1.若,则计算的结果是( )
A. B.130 C. D.290
2.如图所示的图形绕虚线旋转一周,可以得到的几何体是( )
A. B. C. D.
3.如图 , Rt 的直角顶点 在直线 上, 斜边 在直线 上. 若 , 则 ( )
A. B. C. D.
4.若关于x的分式方程的解为非负数,则a的取值范围是( ).
A.a≥1 B.a>1 C.a≥1且a≠4 D.a>1且a≠4
5.若一个三角形三个内角度数的比为2∶3∶5,那么这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定
6.扇文化是中华优秀传统文化的组成部分,在我国有着深厚的底蕴.如图,某折扇张开的角度为时,扇面面积为、该折扇张开的角度为时,扇面面积为,若,则与关系的图象大致是( )
A. B.
C. D.
7.如图,将正方形放在平面直角坐标系中,是原点,的坐标为,则点的坐标为( )
A. B. C. D.
8.科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一段时间后,记录下这种植物高度的增长情况(如下表):
温度x/℃ … ﹣4 ﹣2 0 2 4 6 …
植物每天高度的增长量y/mm … 41 49 49 41 25 1 …
由这些数据,科学家推测出植物每天高度的增长量y是温度x的二次函数,那么下列三个结论:
①该植物在0℃时,每天高度的增长量最大;
②该植物在﹣6℃时,每天高度的增长量能保持在25mm左右;
③该植物与大多数植物不同,6℃以上的环境下高度几乎不增长.
上述结论中,所有正确结论的序号是
①②③ B.①③ C.①② D.②③
第二部分( 非选择题)
二、填空题(共5小题,每小题3分,计15分)
9.因式分解: .
10. 如图是北京和巴黎的时差,则当巴黎时间为8:30时,北京时间为 .
11.如图,是圆的直径,弦、相交于点,点是弧的中点,若,则的值是 .
12.若点,在反比例函数的图象上,则,的大小关系用“<”连接的结果为 .
13.如图,在中,点是角平分线AD,BE的交点,若,则的值是 .
三、解答题(共13小题,计81分。解答题应写出过程)
14.计算
(1)
(1)化简:;
化简:;
先化简,再求值:,其中,.
(1)解分式方程;
先化简,再求值,从,,2中选择合适的的值代入求值.
17.如图所示,已知,,请用尺规作图法在边上确定一点,并连接,使得(保留作图痕迹,不写作法)
18.已知:如图,四边形BCDE是矩形,,求证:.
19.为庆祝中国共产党成立100周年,某中学组织全校学生参加党史知识竞赛,从中任取20名学生的竞赛成绩进行统计,绘制了不完整的统计图表:
组别 成绩范围 频数
A 60~70 2
D 70~80 m
C 80~90 9
D 90~100 n
(1)分别求m,n的值;
(2)从A组和D组的学生中随机抽取2名学生,用树状图或列表法求这2名学生都在D组的概率.
20.某工程队修一段全长6300 m的道路,甲、乙两个班组分别从南、北两端同时施工.已知甲班组比乙班组平均每天多修6m ,经过3天施工,两组共修了180 m.
(1)求甲、乙两个班组平均每天各修多少米
(2)为了方便群众出行,现决定加快进度,在剩余的工程中,甲班组平均每天能比原来多修5m,乙班组平均每天能比原来多修7 m,按此施工进度,能够比原来少用多少天完成任务
21.数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度.如图所示,炎帝塑像DE在高55m的小山EC上,在A处测得塑像底部E的仰角为34° ,再沿AC方向前进21m到达B处,测得塑像顶部D的仰角为60°,求炎帝塑像DE的高度.(精确到1m.参考数据)
22.在平面直角坐标系中,O是坐标原点,定义点A和点B的关联值如下:
若O,A,B在一条直线上;
若O,A,B不在一条直线上.
已知点A坐标为点B坐标为,回答下列问题:
(1)______;
(2)若,,则点P坐标为_______ ;
(3)在图中画出所有满足的点P.
23.习近平总书记指出“餐饮浪费现象,触目惊心,令人心痛”.为此园区某中学开展“厉行勤俭节约,反对铺张浪费”主题活动,为了解学生的参与情况,波波在全校范围内随机抽取了若干名学生就某日午饭浪费饭菜情况进行了调查.将调查内容分为四组:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据调查结果,绘制了如图所示两幅尚不完整的统计图,回答下列问题:
(1)这次被抽查的学生共有________人,扇形统计图中,“B组”所对圆心角的度数为_______;
(2)补全条形统计图;
(3)已知该中学共有学生1500人,请估计这日午饭有剩饭的学生人数,若有剩饭的学生按平均每人剩米饭计算,这日午饭将浪费多少克米饭?
24.如图,是的直径,点D在的延长线上,C、E是上的两点,且,,延长交的延长线于点F.
(1)求证:是的切线;
(2)求证:;
(3)若,,求的半径
25.根据以下素材,探索完成任务.
设计彩虹桥中彩色灯带的悬挂方
素材一 图1是一座隐藏在漳州城市中的“彩虹桥”,也是近年来比较热门的网红打卡点,它由200多个铁架和2400多个灯笼组成.如图2,每个铁架的横截面可以分为3段,其中是固定支架,分别与地面垂直,主体支架可近似看作一段抛物线,最高点离地面的距离是,,.
素材二 由于灯笼颜色比较单一,街道准备把灯笼替换成长度为的彩色灯带,沿抛物线(主体支架)安装(如图3),且相邻两条灯带安装点的水平间距为.为了安全起见,灯带底部与地面的距离不低于.灯带安装好后成轴对称分布.
问题解决
任务一 确定主体支架的形状 请在图2中以点A为原点建立平面直角坐标系,并求出抛物线的解析式.
任务二 探究安装范围 在安全前提下,在任务一的坐标系中,确定灯带安装点的横坐标取值范围.
任务三 拟定设计方案 在同一个横截面下,最多能安装几条灯带?并求出此时最右边灯带安装点的坐标.
26.问题探究如图1,AB是⊙O的直径,.
(1)求∠BAD的度数.
(2)拓展延伸如图2,若,AB与CD的交点记作E,.
①求⊙O的半径;
②如图3,若DF是⊙O的切线,且点F在BA的延长线上,求图3中阴影部分的周长.
答案解析部分
1.A
2.C
解:将所示图形分成两部分,如图:
上面部分是矩形,旋转一周可得圆柱;下面图形是直角三角形,旋转一周可得到圆锥,故组合起来如图所示:
故答案为:C.
将图形分割成常见的矩形和三角形,分别讨论旋转一周形成的几何体即可.
3.C
解:∵,
∴∠ABC=∠1=55°.
∵∠BAC=90°,
∴∠ABC+∠2=90°,
∴55°+∠2=90°,解得∠2=35°.
故答案为:C.
先利用平行线的性质,求得∠ABC,再利用直角三角形两个锐角互余,求出∠2.
4.C
解:∵关于x的分式方程的解为非负数
∴
∴
∴a≥1
∵x-2≠0
∴x≠2,即
解得:a≠4
综上所述: a≥1且a≠4
故答案为:C
去分母,将分式方程化为整式方程,解方程即可求出答案.
5.A
解:设三角形三个内角度数为2x、3x、5x,
,解得,
,
这个三角形是直角三角形.
故答案为:A.
设三角形三个内角度数为2x、3x、5x,利用三角形的内角和定理求得x的值,进而证得这个三角形是直角三角形.
6.C
7.C
8.D
①因为是二次函数,所以设y=ax2+bx+c(a≠0),
∵x= 2时,y=49,
x=0时,y=49,
x=2时,y=41,
分别代入解析式,,解得,
∴,y关于x的函数关系式为;
∵y= x2 2x+49= (x+1)2+50,
A=-1<0,抛物线开口向上,
∴当x= 1时,y有最大值为50,
即当温度为 1℃时,这种作物每天高度增长量最大;①错误.
②把x= -6代入解析式y= x2 2x+49得:y=25,②正确.
③把x= 6代入解析式y= x2 2x+49得:y=1
把x= 7代入解析式y= x2 2x+49得:y= -14<0,③正确.
故选D.
本题考查二次函数的应用 .因为是二次函数,所以设y=ax2+bx+c(a≠0),将x= 2时,y=49;x=0时,y=49;x=2时,y=41;代入二次函数的解析式可列出不等式组,解不等式组可求出a,b,c的值,再对解析式进行配方解得:y= (x+1)2+50,利用二次函数的性质可求出最大值,据此可判断说法 ① ;将x= -6代入函数解析式可求出y的值,据此可判断说法 ② ;把x= 6和x= 7代入函数解析式求出y的值,再进行比较据此可判断说法③.
9.x(2-y)
解:2x-xy=x(2-y)
故答案为:x(2-y).
利用提公因式法进行因式分解即可.
10.15:30
由题意得 巴黎和北京的时差为7小时,则北京时间为8:30+7=15:30
故答案为:15:30
根据题意可得巴黎和北京的时差为7小时,则北京时间为8:30+7=15:30。
11.
12.
解:∵点,在反比例函数 ,∴
故.
故答案为:.
本题主要考查反比例函数的性质,根据题意将点A、B代入反比函数的解析可得:即可求解.
13.
解:作于点F,
∵,AD平分∠ABC,
∴,
∵O为角平分线AD,BE的交点,,,
∴,
∴,
∵,
∴,
∴,解得,
∴.
故答案为:.
作于点F,利用等腰三角形三线合一的性质可得,,利用角平分线的性质可得,由勾股定理求出AD=8,再利用△OBD和△OBA的面积可推出,即得,据此求出OD=3,利用即可求解.
14.(1)解:原式=-0.5-2
=-2
(2)解:原式=-4+3-3+2-
=-2-
(1)先求出原式中算术平方根、立方根再进行计算即可;
(2)根据平方的意义、算术平方根的意义以及立方根的意义、绝对值的性质逐步计算即可求得答案.
15.(1)解:
;
(2)解:
;
(3)解:原式
,
当,时,原式.
(1)合并同类项即可求出答案.
(2)合并同类项即可求出答案.
(3)去括号,合并同类项,再将,代入即可求出答案.
16.(1)
(2)原式,,原式
17.解:如图,过C点作CP⊥AB于P点,则点P即为所作.
先过C点作CP⊥AB于P点,由于∠B=45°,则根据有一个角是45°的直角三角形是等腰直角三角形,等腰直角三角形的两底角所对的边相等可得PB=PC,根据勾股定理:直角三角形中两直角边的平方和等于斜边的平方可得AP2+PC2=AC2,即可得到AP2+PB2=AC2.
18.证明:∵四边形BCDE是矩形,
∴,,
∵,
∴,
∴,
∴,
∴
∴.
先根据矩形的性质得,,再根据全等三角形的判定SAS证出,得到即可.
19.(1)解: 由题意得:n=20×20%=4,
则m=20-2-9-4=5,
(2)解: A组有2名学生,D组有4名学生,
画树状图如图:
共有30种等可能的结果,抽取的2名学生都在D组的结果有12种,
∴抽取的2名学生都在D组的概率为=
(1)根据频数的计算方法结合题意即可求解;
(2)先根据题意画出树状图,进而得到共有30种等可能的结果,抽取的2名学生都在D组的结果有12种,再运用等可能事件的概率即可求解。
20.(1)解:设乙班组每天修x(m),则甲班组每天修(x+6)m.
由题意,得3x+3(x+6)=180,解得x=27,∴x+6=33.
答:甲、乙两个班组平均每天各修33 m,27 m.
(2)解:改进施工技术后,甲班组每天修33+5=38(m),乙班组每天修27+7=34(m).
原来一共需要修 (天),改进施工技术后一共需要修 =3+85=88(天), (天).
答:按此施工进度,能够比原来少用17天完成任务.
(1)通过设未知数x,分别表示出甲、乙两个组每天修路的长度,再根据条件“ 经过3天施工,两组共修了180 m ”即可累出等式,求出x的值,继而求出 甲、乙两个班组平均每天各修多少米 ;
(2)先根据条件,可求出改进施工技术后,甲乙两个组每天的施工长度,分别再算出改进施工技术前后,各需要修多少天,再把两个结果做差,即可求出答案。
21.解:,
,
,
在Rt中,,
答:炎帝塑像DE的高度约为51m.
先根据正切函数得到,进而即可求出AC,再进行线段的运算得到BC,从而根据特殊角的三角函数值即可求出CD,最后根据DE=CD-EC即可求解。
22.(1)8
(2)或
(3)一三象限角平分线或二四象限角平分线
23.解:(1)120,72°
(2)C组的人数为:120×10%=12(人),补全条形统计图如下:
(3)这日午饭有剩饭的学生人数为:1500×=450(人),
450×20=9000(克)=9(千克),
答:这日午饭将浪费了9千克米饭.
(1) 这次被抽查的学生数是:72÷60%=120(人),“B组”所对应的圆心角的度数为:360°×=72°.
故答案为:120,72°.
(1)根据扇形统计图,得到A组人数所占百分比,用A组人数除以它所占的百分比,得到调查的总人数;再求出B组所占的百分比,再乘以360°,得出“B组”所对应的圆心角的度数;
(2)根据扇形统计图,得到C组人数所占百分比,用调查的总人数乘以C组所占的百分比,得出C组的人数,进而补全条形统计图;
(3)用总人数乘以午饭有剩饭的学生人数所占的百分比,求出这日午饭有剩饭的学生人数,再乘以平均每人剩米饭的克数,即可得出午饭浪费的总克数.
24.(1)连接,如图所示,
∵是的直径,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵为圆的半径,
∴是的切线;
(2)∵,
∴,
∴,
又∵,
∴;
(3)在中,,
∴,
∵
解得:,
的半径为
本题考查切线的判定、等腰三角形的性质、全等三角形的判定和性质、勾股定理.(1)连接,根据是的直径,利用圆周角定理可得:,根据, 利用等边对等角和角的运算可得:,根据,利用等边对等角可得,再根据,可得出,利用圆的切线的判定定理可证明结论;
(2)根据,利用全等三角形的判定定理可证明,利用全等三角形的性质可得,又,利用等量代换可证明结论;
(3)在中,利用勾股定理可得:,代入数据可列出方程,解方程可求出的长.
25.任务一:;任务二:;任务三:
26.(1)解:如图1,连接BD,
∵AB是⊙O的直径,∴.
∵,∴.
(2)解:①如图2,连接OC.
∵,AB是⊙O的直径,∴,,
∴.
设⊙O的半径为r,则.
∵在Rt△COE中,,∴,即,解得.
②如图3,连接OD.
∵,∴.
由①可得⊙O的半径为,∴的长为.
∵DF是⊙O的切线,∴.
∵在Rt△ODF中,,∴,∴,
∴,
∴,
∴阴影部分的周长为.
(1)连接BD,先根据圆周角定理得到,进而结合题意进行角的运算即可求解;
(2)①连接OC,先根据圆周角定理结合等腰三角形的性质得到,,进而得到∠OEC的度数,设⊙O的半径为r,则,再根据题意解直角三角形即可求解;
②连接OD,进而根据圆周角定理得到,由①可得⊙O的半径为,进而根据弧长的计算公式得到的长,再根据切线的性质得到,再解直角三角形得到OF和AF,从而根据“阴影部分的周长为”即可求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
机密★启用前
2025 年 陕 西 省 中 考 一 模 猜 题 卷
数 学
注意事项:
I.本试卷分为第一部分( 选择题) 和第二部分( 非选择题). 全卷共8 页,总分120 分。
考试时间120 分钟。
2.领到试卷和答题卡后,请用0.5毫米黑色墨水签字笔, 分别在试卷和答题卡上填写姓
名和准考证号,同时用2B 铅笔在答题卡上填涂对应的试卷类型信息点(A 或B)。
3.请在答題卡上各题的指定区域内作答, 否则作答无效。
4.作图时,先用铅笔作图, 再用规定签字笔描黑。
5.考试结束,本试卷和答题卡一并交回。
第一部分( 选择题)
一、选择题(共8小题,每小题3分,计24分,每小题只有一个选项是符合题意的)
1.若,则计算的结果是( )
A. B.130 C. D.290
2.如图所示的图形绕虚线旋转一周,可以得到的几何体是( )
A. B. C. D.
3.如图 , Rt 的直角顶点 在直线 上, 斜边 在直线 上. 若 , 则 ( )
A. B. C. D.
4.若关于x的分式方程的解为非负数,则a的取值范围是( ).
A.a≥1 B.a>1 C.a≥1且a≠4 D.a>1且a≠4
5.若一个三角形三个内角度数的比为2∶3∶5,那么这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定
6.扇文化是中华优秀传统文化的组成部分,在我国有着深厚的底蕴.如图,某折扇张开的角度为时,扇面面积为、该折扇张开的角度为时,扇面面积为,若,则与关系的图象大致是( )
A. B.
C. D.
7.如图,将正方形放在平面直角坐标系中,是原点,的坐标为,则点的坐标为( )
A. B. C. D.
8.科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一段时间后,记录下这种植物高度的增长情况(如下表):
温度x/℃ … ﹣4 ﹣2 0 2 4 6 …
植物每天高度的增长量y/mm … 41 49 49 41 25 1 …
由这些数据,科学家推测出植物每天高度的增长量y是温度x的二次函数,那么下列三个结论:
①该植物在0℃时,每天高度的增长量最大;
②该植物在﹣6℃时,每天高度的增长量能保持在25mm左右;
③该植物与大多数植物不同,6℃以上的环境下高度几乎不增长.
上述结论中,所有正确结论的序号是
①②③ B.①③ C.①② D.②③
第二部分( 非选择题)
二、填空题(共5小题,每小题3分,计15分)
9.因式分解: .
10. 如图是北京和巴黎的时差,则当巴黎时间为8:30时,北京时间为 .
11.如图,是圆的直径,弦、相交于点,点是弧的中点,若,则的值是 .
12.若点,在反比例函数的图象上,则,的大小关系用“<”连接的结果为 .
13.如图,在中,点是角平分线AD,BE的交点,若,则的值是 .
三、解答题(共13小题,计81分。解答题应写出过程)
14.计算
(1)
(1)化简:;
化简:;
先化简,再求值:,其中,.
(1)解分式方程;
先化简,再求值,从,,2中选择合适的的值代入求值.
17.如图所示,已知,,请用尺规作图法在边上确定一点,并连接,使得(保留作图痕迹,不写作法)
18.已知:如图,四边形BCDE是矩形,,求证:.
19.为庆祝中国共产党成立100周年,某中学组织全校学生参加党史知识竞赛,从中任取20名学生的竞赛成绩进行统计,绘制了不完整的统计图表:
组别 成绩范围 频数
A 60~70 2
D 70~80 m
C 80~90 9
D 90~100 n
(1)分别求m,n的值;
(2)从A组和D组的学生中随机抽取2名学生,用树状图或列表法求这2名学生都在D组的概率.
20.某工程队修一段全长6300 m的道路,甲、乙两个班组分别从南、北两端同时施工.已知甲班组比乙班组平均每天多修6m ,经过3天施工,两组共修了180 m.
(1)求甲、乙两个班组平均每天各修多少米
(2)为了方便群众出行,现决定加快进度,在剩余的工程中,甲班组平均每天能比原来多修5m,乙班组平均每天能比原来多修7 m,按此施工进度,能够比原来少用多少天完成任务
21.数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度.如图所示,炎帝塑像DE在高55m的小山EC上,在A处测得塑像底部E的仰角为34° ,再沿AC方向前进21m到达B处,测得塑像顶部D的仰角为60°,求炎帝塑像DE的高度.(精确到1m.参考数据)
22.在平面直角坐标系中,O是坐标原点,定义点A和点B的关联值如下:
若O,A,B在一条直线上;
若O,A,B不在一条直线上.
已知点A坐标为点B坐标为,回答下列问题:
(1)______;
(2)若,,则点P坐标为_______ ;
(3)在图中画出所有满足的点P.
23.习近平总书记指出“餐饮浪费现象,触目惊心,令人心痛”.为此园区某中学开展“厉行勤俭节约,反对铺张浪费”主题活动,为了解学生的参与情况,波波在全校范围内随机抽取了若干名学生就某日午饭浪费饭菜情况进行了调查.将调查内容分为四组:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据调查结果,绘制了如图所示两幅尚不完整的统计图,回答下列问题:
(1)这次被抽查的学生共有________人,扇形统计图中,“B组”所对圆心角的度数为_______;
(2)补全条形统计图;
(3)已知该中学共有学生1500人,请估计这日午饭有剩饭的学生人数,若有剩饭的学生按平均每人剩米饭计算,这日午饭将浪费多少克米饭?
24.如图,是的直径,点D在的延长线上,C、E是上的两点,且,,延长交的延长线于点F.
(1)求证:是的切线;
(2)求证:;
(3)若,,求的半径
25.根据以下素材,探索完成任务.
设计彩虹桥中彩色灯带的悬挂方
素材一 图1是一座隐藏在漳州城市中的“彩虹桥”,也是近年来比较热门的网红打卡点,它由200多个铁架和2400多个灯笼组成.如图2,每个铁架的横截面可以分为3段,其中是固定支架,分别与地面垂直,主体支架可近似看作一段抛物线,最高点离地面的距离是,,.
素材二 由于灯笼颜色比较单一,街道准备把灯笼替换成长度为的彩色灯带,沿抛物线(主体支架)安装(如图3),且相邻两条灯带安装点的水平间距为.为了安全起见,灯带底部与地面的距离不低于.灯带安装好后成轴对称分布.
问题解决
任务一 确定主体支架的形状 请在图2中以点A为原点建立平面直角坐标系,并求出抛物线的解析式.
任务二 探究安装范围 在安全前提下,在任务一的坐标系中,确定灯带安装点的横坐标取值范围.
任务三 拟定设计方案 在同一个横截面下,最多能安装几条灯带?并求出此时最右边灯带安装点的坐标.
26.问题探究如图1,AB是⊙O的直径,.
(1)求∠BAD的度数.
(2)拓展延伸如图2,若,AB与CD的交点记作E,.
①求⊙O的半径;
②如图3,若DF是⊙O的切线,且点F在BA的延长线上,求图3中阴影部分的周长.
答案解析部分
1.A
2.C
解:将所示图形分成两部分,如图:
上面部分是矩形,旋转一周可得圆柱;下面图形是直角三角形,旋转一周可得到圆锥,故组合起来如图所示:
故答案为:C.
将图形分割成常见的矩形和三角形,分别讨论旋转一周形成的几何体即可.
3.C
解:∵,
∴∠ABC=∠1=55°.
∵∠BAC=90°,
∴∠ABC+∠2=90°,
∴55°+∠2=90°,解得∠2=35°.
故答案为:C.
先利用平行线的性质,求得∠ABC,再利用直角三角形两个锐角互余,求出∠2.
4.C
解:∵关于x的分式方程的解为非负数
∴
∴
∴a≥1
∵x-2≠0
∴x≠2,即
解得:a≠4
综上所述: a≥1且a≠4
故答案为:C
去分母,将分式方程化为整式方程,解方程即可求出答案.
5.A
解:设三角形三个内角度数为2x、3x、5x,
,解得,
,
这个三角形是直角三角形.
故答案为:A.
设三角形三个内角度数为2x、3x、5x,利用三角形的内角和定理求得x的值,进而证得这个三角形是直角三角形.
6.C
7.C
8.D
①因为是二次函数,所以设y=ax2+bx+c(a≠0),
∵x= 2时,y=49,
x=0时,y=49,
x=2时,y=41,
分别代入解析式,,解得,
∴,y关于x的函数关系式为;
∵y= x2 2x+49= (x+1)2+50,
A=-1<0,抛物线开口向上,
∴当x= 1时,y有最大值为50,
即当温度为 1℃时,这种作物每天高度增长量最大;①错误.
②把x= -6代入解析式y= x2 2x+49得:y=25,②正确.
③把x= 6代入解析式y= x2 2x+49得:y=1
把x= 7代入解析式y= x2 2x+49得:y= -14<0,③正确.
故选D.
本题考查二次函数的应用 .因为是二次函数,所以设y=ax2+bx+c(a≠0),将x= 2时,y=49;x=0时,y=49;x=2时,y=41;代入二次函数的解析式可列出不等式组,解不等式组可求出a,b,c的值,再对解析式进行配方解得:y= (x+1)2+50,利用二次函数的性质可求出最大值,据此可判断说法 ① ;将x= -6代入函数解析式可求出y的值,据此可判断说法 ② ;把x= 6和x= 7代入函数解析式求出y的值,再进行比较据此可判断说法③.
9.x(2-y)
解:2x-xy=x(2-y)
故答案为:x(2-y).
利用提公因式法进行因式分解即可.
10.15:30
由题意得 巴黎和北京的时差为7小时,则北京时间为8:30+7=15:30
故答案为:15:30
根据题意可得巴黎和北京的时差为7小时,则北京时间为8:30+7=15:30。
11.
12.
解:∵点,在反比例函数 ,∴
故.
故答案为:.
本题主要考查反比例函数的性质,根据题意将点A、B代入反比函数的解析可得:即可求解.
13.
解:作于点F,
∵,AD平分∠ABC,
∴,
∵O为角平分线AD,BE的交点,,,
∴,
∴,
∵,
∴,
∴,解得,
∴.
故答案为:.
作于点F,利用等腰三角形三线合一的性质可得,,利用角平分线的性质可得,由勾股定理求出AD=8,再利用△OBD和△OBA的面积可推出,即得,据此求出OD=3,利用即可求解.
14.(1)解:原式=-0.5-2
=-2
(2)解:原式=-4+3-3+2-
=-2-
(1)先求出原式中算术平方根、立方根再进行计算即可;
(2)根据平方的意义、算术平方根的意义以及立方根的意义、绝对值的性质逐步计算即可求得答案.
15.(1)解:
;
(2)解:
;
(3)解:原式
,
当,时,原式.
(1)合并同类项即可求出答案.
(2)合并同类项即可求出答案.
(3)去括号,合并同类项,再将,代入即可求出答案.
16.(1)
(2)原式,,原式
17.解:如图,过C点作CP⊥AB于P点,则点P即为所作.
先过C点作CP⊥AB于P点,由于∠B=45°,则根据有一个角是45°的直角三角形是等腰直角三角形,等腰直角三角形的两底角所对的边相等可得PB=PC,根据勾股定理:直角三角形中两直角边的平方和等于斜边的平方可得AP2+PC2=AC2,即可得到AP2+PB2=AC2.
18.证明:∵四边形BCDE是矩形,
∴,,
∵,
∴,
∴,
∴,
∴
∴.
先根据矩形的性质得,,再根据全等三角形的判定SAS证出,得到即可.
19.(1)解: 由题意得:n=20×20%=4,
则m=20-2-9-4=5,
(2)解: A组有2名学生,D组有4名学生,
画树状图如图:
共有30种等可能的结果,抽取的2名学生都在D组的结果有12种,
∴抽取的2名学生都在D组的概率为=
(1)根据频数的计算方法结合题意即可求解;
(2)先根据题意画出树状图,进而得到共有30种等可能的结果,抽取的2名学生都在D组的结果有12种,再运用等可能事件的概率即可求解。
20.(1)解:设乙班组每天修x(m),则甲班组每天修(x+6)m.
由题意,得3x+3(x+6)=180,解得x=27,∴x+6=33.
答:甲、乙两个班组平均每天各修33 m,27 m.
(2)解:改进施工技术后,甲班组每天修33+5=38(m),乙班组每天修27+7=34(m).
原来一共需要修 (天),改进施工技术后一共需要修 =3+85=88(天), (天).
答:按此施工进度,能够比原来少用17天完成任务.
(1)通过设未知数x,分别表示出甲、乙两个组每天修路的长度,再根据条件“ 经过3天施工,两组共修了180 m ”即可累出等式,求出x的值,继而求出 甲、乙两个班组平均每天各修多少米 ;
(2)先根据条件,可求出改进施工技术后,甲乙两个组每天的施工长度,分别再算出改进施工技术前后,各需要修多少天,再把两个结果做差,即可求出答案。
21.解:,
,
,
在Rt中,,
答:炎帝塑像DE的高度约为51m.
先根据正切函数得到,进而即可求出AC,再进行线段的运算得到BC,从而根据特殊角的三角函数值即可求出CD,最后根据DE=CD-EC即可求解。
22.(1)8
(2)或
(3)一三象限角平分线或二四象限角平分线
23.解:(1)120,72°
(2)C组的人数为:120×10%=12(人),补全条形统计图如下:
(3)这日午饭有剩饭的学生人数为:1500×=450(人),
450×20=9000(克)=9(千克),
答:这日午饭将浪费了9千克米饭.
(1) 这次被抽查的学生数是:72÷60%=120(人),“B组”所对应的圆心角的度数为:360°×=72°.
故答案为:120,72°.
(1)根据扇形统计图,得到A组人数所占百分比,用A组人数除以它所占的百分比,得到调查的总人数;再求出B组所占的百分比,再乘以360°,得出“B组”所对应的圆心角的度数;
(2)根据扇形统计图,得到C组人数所占百分比,用调查的总人数乘以C组所占的百分比,得出C组的人数,进而补全条形统计图;
(3)用总人数乘以午饭有剩饭的学生人数所占的百分比,求出这日午饭有剩饭的学生人数,再乘以平均每人剩米饭的克数,即可得出午饭浪费的总克数.
24.(1)连接,如图所示,
∵是的直径,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵为圆的半径,
∴是的切线;
(2)∵,
∴,
∴,
又∵,
∴;
(3)在中,,
∴,
∵
解得:,
的半径为
本题考查切线的判定、等腰三角形的性质、全等三角形的判定和性质、勾股定理.(1)连接,根据是的直径,利用圆周角定理可得:,根据, 利用等边对等角和角的运算可得:,根据,利用等边对等角可得,再根据,可得出,利用圆的切线的判定定理可证明结论;
(2)根据,利用全等三角形的判定定理可证明,利用全等三角形的性质可得,又,利用等量代换可证明结论;
(3)在中,利用勾股定理可得:,代入数据可列出方程,解方程可求出的长.
25.任务一:;任务二:;任务三:
26.(1)解:如图1,连接BD,
∵AB是⊙O的直径,∴.
∵,∴.
(2)解:①如图2,连接OC.
∵,AB是⊙O的直径,∴,,
∴.
设⊙O的半径为r,则.
∵在Rt△COE中,,∴,即,解得.
②如图3,连接OD.
∵,∴.
由①可得⊙O的半径为,∴的长为.
∵DF是⊙O的切线,∴.
∵在Rt△ODF中,,∴,∴,
∴,
∴,
∴阴影部分的周长为.
(1)连接BD,先根据圆周角定理得到,进而结合题意进行角的运算即可求解;
(2)①连接OC,先根据圆周角定理结合等腰三角形的性质得到,,进而得到∠OEC的度数,设⊙O的半径为r,则,再根据题意解直角三角形即可求解;
②连接OD,进而根据圆周角定理得到,由①可得⊙O的半径为,进而根据弧长的计算公式得到的长,再根据切线的性质得到,再解直角三角形得到OF和AF,从而根据“阴影部分的周长为”即可求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
