2025年中考数学一模猜题卷(上海专用)—2025年全国各地市最新中考数学模拟考试(含答案)
文档属性
| 名称 | 2025年中考数学一模猜题卷(上海专用)—2025年全国各地市最新中考数学模拟考试(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 20:57:36 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2 0 2 5 年 上 海 市 中 考 一 模 猜 题 卷
数 学 试 卷
姓名 ________准考证号________ 考场号 ________ 座位号________
1.本场考试时间100分钟.试卷共4页,满分150分,答题纸共2页
2.作答前,请在答题纸指定位置填写姓名、报名号、座位号.并将核对后的条形码贴在答题纸指定位置
3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域,不得错位.在试卷上作答一律不得分
4.用2B铅笔作答选择题,用黑色字迹钢笔、水笔或圆珠笔作答非
一、选择题(每题4分,共24分)
1.下列关系不正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.函数的自变量x的取值范围是( )
A. B. C. D.
3.若关于的一元二次方程有两个不相等的实数根,则的最小整数值为( )
A. B.0 C.1 D.2
4.为了解某公司的收入水平,随机挑选五人的月工资进行抽样调查,月工资(单位:元)分别是3000,4000,5000,6000,50000,那么能够较好的反映他们收入平均水平的是( )
A.中位数 B.标准差 C.平均数 D.众数
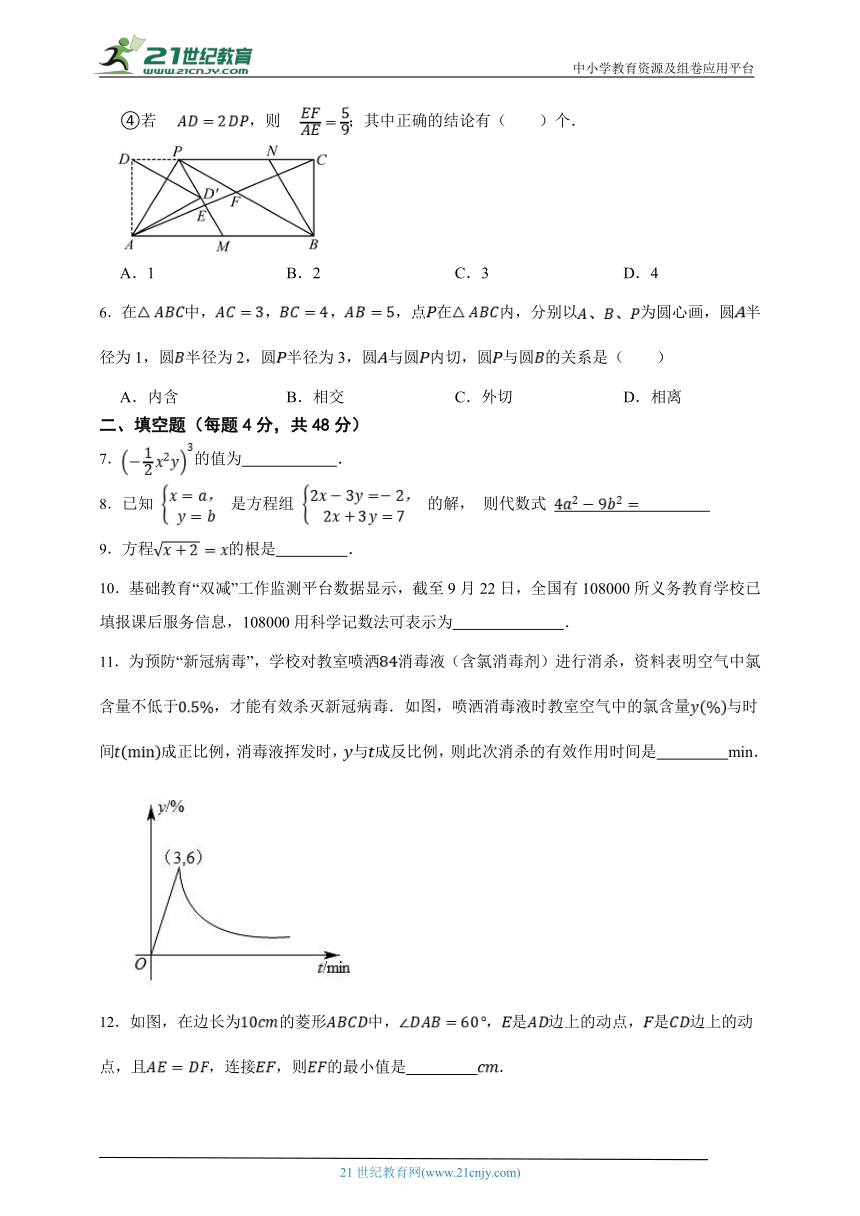
5.如图,在矩形中,为边上一点,.将沿翻折得到,的延长线交边于点,过点作交于点,连接,分别交于点E,F.现有以下结论:
①连接,则垂直平分;
②四边形是菱形;
③;
④若,则;其中正确的结论有( )个.
A.1 B.2 C.3 D.4
6.在中,,,,点在内,分别以为圆心画,圆半径为1,圆半径为2,圆半径为3,圆与圆内切,圆与圆的关系是( )
A.内含 B.相交 C.外切 D.相离
二、填空题(每题4分,共48分)
7.的值为 .
8.已知 是方程组 的解, 则代数式
9.方程的根是 .
10.基础教育“双减”工作监测平台数据显示,截至9月22日,全国有108000所义务教育学校已填报课后服务信息,108000用科学记数法可表示为 .
11.为预防“新冠病毒”,学校对教室喷洒消毒液(含氯消毒剂)进行消杀,资料表明空气中氯含量不低于,才能有效杀灭新冠病毒.如图,喷洒消毒液时教室空气中的氯含量与时间成正比例,消毒液挥发时,与成反比例,则此次消杀的有效作用时间是 min.
12.如图,在边长为的菱形中,,是边上的动点,是边上的动点,且,连接,则的最小值是 .
13.一辆汽车在行驶过程中,其行驶路程(千米)与行驶时间(小时)之间的函数关系如图所示.当时,与之间的函数表达式为;当时,与之间的函数表达式为 .
14.掷一枚六个面分别标有1,2,3,4,5,6的正方形骰子,则向上一面的数不大于5的概率是 .
15.计算: .
16.从一口鱼塘里随机捞出10条鱼,在这些鱼身上做上记号,然后把鱼放回鱼池.过一段时间后,在同样的地方再捞出100条鱼,其中带有记号的鱼有2条,根据抽样调查的方法,估计整个鱼塘约有鱼 条.
17.如图,有一张平行四边形纸条 ABCD,AD=5cm,AB=2cm, ∠A=120°, 点E,F 分别在边 AD,BC上,DE=1cm. 现将四边形 CFED沿EF折叠,使点C,D 分别落在点C’,D '上.当点C’恰好落在边AD上时,线段 CF的长为 cm .在点F 从点B 运动到点C的过程中,若边与边AD交于点M, 则点M相应运动的路径长为 cm.
18. 定义为二次函数的特征数,下面给出特征数为的函数结论,其中正确的结论是 .(填写序号)
①当时,点一定在函数的图象上;
②当时,函数图象截x轴所得的线段长度大于;
③当时,函数在时,y随x的增大而增大;
④若抛物线的顶点与抛物线与x轴两交点组成的三角形为等腰直角三角形,则
三、简答题(共78分,其中第19-22题每题10分,第23、24题每题12分,第25题14分)
19.计算:
(1);
(2).
解方程组:
.
21.如图,一次函数的图象与反比例函数的图象交于,两点.
(1)求反比例函数和一次函数的表达式.
(2)求的面积.
(3)当时,直接写出x的取值范围.
22.如图,在矩形中,,为边上一点,,连接.动点从点同时出发,点以的速度沿向终点运动;点以的速度沿折线向终点运动.设点运动的时间为,在运动过程中,点,点经过的路线与线段围成的图形面积为.
(1) , ;
(2)求关于的函数解析式,并写出自变量的取值范围;
(3)当时,直接写出的值.
23.如图,在矩形中,E,F分别是边上的点,,将沿翻折,C点的对应点为G.
(1)如图(1),若点G正好落在上.求证:;
(2)如图(2),若点G落在矩形的内部,且,延长交于点H,求证:;
(3)在(1)的条件下,若,.请直接写出的长度.
24. 如图1,直线与轴,轴分别交于点,,抛物线的顶点在直线上,与轴的交点为,,其中点的坐标为,直线与直线相交于点.
图1 图2 备用图
(1)如图2,若抛物线经过原点.
①求该抛物线的函数表达式;
②求的值;
抛物线的顶点在直线上运动的过程中,请问与能否相等?若能,请直接写出符合条件的点的横坐标;若不能,试说明理由.
25.如图①.在矩形.,点在边上,且.动点从点出发,沿折线以每秒个单位长度的速度运动,作,交边或边于点,连续.当点与点重合时,点停止运动.设点的运动时间为秒.()
(1)当点和点重合时,线段的长为 ;
(2)当点和点重合时,求;
(3)当点在边上运动时,的形状始终是等腰直角三角形.如图②.请说明理由;
(4)作点关于直线的对称点,连接、,当四边形和矩形重叠部分图形为轴对称四边形时,直接写出的取值范围.
答案解析部分
1.D
2.D
解:由题意可知,,
解得:,
故答案为:D.
利用二次根式有意义的条件(被开方数大于等于0)列出不等式求解即可.
3.D
4.A
5.C
6.B
解:如图,
∵ 圆与圆内切, 圆半径为1,圆半径为3,
∴ AP1=3-1=2
∴ BP1=AB-AP1=3
∵ AC=3,
∴ CP2=AC-AP2=1
∴ BP2=
∴ 3<BP<
∵ rB=2
∴ rB+rP=5,rB-rP=1
∴1<BP<5
∴ 圆P与圆B相交
故答案为:B
本题考查圆与圆的位置关系,两圆相交, 圆心距小于两圆半径的和,而大于两圆半径的差的绝对值。根据两圆半径和圆心距,可判定圆与圆的位置关系:设两个圆的半径为R和r,圆心距为d。
(1)d>R+r 两圆外离; 两圆的圆心距离之和大于两圆的半径之和。(2)d=R+r 两圆外切; 两圆的圆心距离之和等于两圆的半径之和。(3)d=R-r 两圆内切; 两圆的圆心距离之和等于两圆的半径之差。(4)d7.
8.-14
解:∵ 是方程组 的解,
∴,两式相乘,得-14.
故答案为:-14.
根据方程组解的意义,将解代入,再将两式相乘,得到待求式子的值.
9.x=2
方程两边平方得:
∴,
∵
∴
∴不符合题意,故舍去
∴原方程的根为x=2
故答案为:x=2.
将方程两边平方得,再求解即可。
10.
解:108000=,
故答案为:.
利用科学记数法的定义:把一个数写成a×10n的形式(其中1≤a<10,n为整数),这种记数法称为科学记数法,其方法如下:①确定a,a是只有一位整数的数,②确定n,当原数的绝对值≥10时,n为正整数,n等于原数的整数位数减1;当原数的绝对值<1,n为负整数,n的绝对值等于原数中左起第一个非0数前0的个数(含整数位上的0),再分析求解即可.
11.
12.
13.
解:当时,当x=0.5时,y=30,
当时,设与之间的函数表达式为y=kx+b,
将点(0.5,30),(2,150)代入得,
解得,
∴,
故答案为:
运用待定系数法求一次函数结合题意即可求解。
14.
15.
解:
,
故答案为:.
根据向量的运算法则进行计算可得答案。
16.500
17.;
解:如图,当点C恰好落在边AD上时,
∵四边形ABCD是平行四边形,且AD=5cm,AB=2cm, ∠A=120°, ∴CD=AB=2cm,∠D=60°,∠BCD=120°,AD∥BC,
∴∠CFE=∠C'EF,
由折叠性质得C'D'=CD=2cm,DE=D'E=1cm,∠D=∠D'=60°,∠CFE=∠C'FE,CF=C'F,
∴∠C'FE=∠C'EF,
∴C'E=C'F=CF,
过点E作EK⊥C'D'于点K,则∠EKD'=∠C'KE=90°,
∴∠KED'=30°,KD'=ED'=cm,
∴,C'K=C'D'-KD'=cm,
∴C'E=,
∴CF=cm;
当点F与点B重合时,AM最短,如图,
∵C'E=cm,C'D'=2cm,D'E=1cm,
∴D'E2+C'E2=4=D'C'2,
∴∠C'ED=90°,
∴∠EC'D'=30°,
∴∠MC'E=∠BC'D'-∠EC'D'=∠BCD-∠EC'D'=90°,
同前面可得BM=ME,设BM=ME=x,则C'M=BC'-BM=BC-BM=5-x,
在Rt△MC'E中,由勾股定理得ME2=C'E2+C'M2,即x2+3+(5-x)2,
解得x=,
∴AM=AD-DE-ME=;
当点C'在AD上时,此时M与点C'重合,如图,
由前面可得AM=AD-DE-C'E=4-cm,
∴点M的运动路程长为:4--=(2.8-)cm.
故答案为:2.8-.
当点C恰好落在边AD上时,易得CD=AB=2cm,∠D=60°,∠BCD=120°,AD∥BC,得∠CFE=∠C'EF,由折叠C'D'=CD=2cm,DE=D'E=1cm,∠D=∠D'=60°,∠CFE=∠C'FE,CF=C'F,则∠C'FE=∠C'EF,由等角对等边得C'E=C'F=CF,过点E作EK⊥C'D'于点K,则∠EKD'=∠C'KE=90°,根据含30°角直角三角形的性质及勾股定理可算出EK的长,进而由线段的和差可得C'K的长,再根据勾股定理算出C'E的长,从而即可求出CF的长;当点F与点B重合时,AM最短,如图,由勾股定理的逆定理判断出∠C'ED=90°,由三角形的内角和定理得∠EC'D'=30°,由角的和差得∠MC'E=90°,同前面可得BM=ME,设BM=ME=x,则C'M=BC'-BM=BC-BM=5-x,在Rt△MC'E中,由勾股定理建立方程可求出x的值,从而求出AM的长;当点C'在AD上时,此时M与点C'重合,如图,由前面可得AM的长,进而即可求出点M运动的路径长.
18.①②③
解:根据题意可得:二次函数解析式为,
当时,,
∴点一定在函数的图象上;
①正确;
当时,,
因式分解得
解得
函数图象截x轴所得的线段长度
②正确;
当时,
∴,抛物线开口向下,在对称轴右侧y随x的增大而减小,
对称轴为,
函数在时, 在对称轴左侧,y随x的增大而增大;
③正确;
④抛物线顶点的纵坐标为,
由②知抛物线与x轴两个交点坐标为解得,
∴两交点的距离为
∵抛物线的顶点与抛物线与x轴两交点组成的三角形为等腰直角三角形,
列方程得
解得,
经检验符合题意,是原方程的根,
④错误;
故答案为:①②③.
利用函数特征数可得二次函数解析式为,当时,把代入函数,求得可判断①,当时,,求出作差可判断②;当时, ,抛物线开口向下,在对称轴右侧y随x的增大而减小,对称轴为可判断③;若抛物线的顶点与抛物线与x轴两交点组成的三角形为等腰直角三角形,根据两交点关于对称轴对称构造方程,解得,可判断④.
19.(1)解:
;
(2)解:
.
(1)根据负整数指数幂运算法则、零指数幂运算法则及有理数的乘方运算法则分别计算,进而计算有理数的加减法运算即可;
(2)根据多项式除以单项式运算法则(多项式除以单项式,用多项式的每一项分别去除以单项式,再把所得的商相加)进行计算即可.
20.解:,
由得:代入中得:
,
,
,
,
解得:或,
当时,,
当时,,
∴方程组的解为或者.
本题考查解二元二次方程组,根据方程组的特点,用代入法求解比较简便。
21.(1)解:将A(-2,1)代入 得.
∴反比例函数的解析式为.
当x=1时,y2=-2, 即B坐标为.
将A,B两点坐标代入一次函数得,
,解得.
∴一次函数解析式为.
(2)解:设直线与x轴的交于M.
当时,,解得,即M.
∴.
(3)或
解:(3)当时,一次函数图象在反比例函数图象的上方,由图象可知,对应图象在A点左侧,即,或者O点和B点之间,即,
∴当时,x的取值范围是:或.
(1)先利用A点坐标求得反比例函数解析式,再求得B的坐标,利用待定系数法,将A、B代入求得一次函数的解析式;
(2)先求出直线与x轴的交点M,由进行计算即可;
(3)当时,一次函数图象在反比例函数图象的上方,结合函数图象即可得到x范围.
(1)解:将A点坐标代入反比例函数得,.
∴反比例函数的解析式为.
将B点坐标代入反比例函数解析式得,.
即点B的坐标为.
将A,B两点坐标代入一次函数解析式得,
,解得.
∴一次函数解析式为.
(2)令直线与x轴的交点为M.
将代入一次函数解析式得,,解得
即点M的坐标为.
∴,,
故.
(3)由函数图象可知,
在直线的左侧和直线与直线之间的部分,
一次函数的图象在反比例函数图象的上方,即,
∴当时,x的取值范围是:或.
22.(1);45°
(2)①当0<x≤2时,如图,过点P作PF⊥AD于点F,
∵cm,cm,
∴cm,
∴,
∴;
②当2<x≤3时,如图,过点P作PF⊥AD于点F,连接PD,
∵cm,cm,
∴
,
即;
③当3<x≤时,如图,点P与点E重合,
∵cm,cm,
∴
,
即,
综上:;
(3)解:或.
解:(1)∵AB=3,BE=AB=3
∴
∴
故答案为:第1空、
第2空、45°
(3)①当0<x≤2时,如图,
∵cm,cm,
∴cm,
当cm时,,解得;
②当2<x≤3时,如图,过点P作PM⊥CD于点M,过点P作于点F,
∵四边形MPFD是矩形,
∴cm,cm,cm,
∵,
∴,解得,
∵,
∴没有在范围内的x的值;
③当3<x≤时,如图,
∵cm,cm,,
∴,解得,(舍去),
∴,
综上:或.
(1)根据勾股定理可求出AE长,再根据等腰直角三角形性质可求出∠EAD的度数.
(2)分三种情况,画出图象,根据点的运动速度用x表示线段长度,由面积和差关系即可求出答案.
(3)分三种情况,画出图象,根据点的运动速度用x表示线段长度,根据勾股定理列出方程,解方程即可求出答案.
23.(1)解:∵四边形是矩形,
∴,
∴,
∵将沿翻折,C点的对应点为G、点G正好落在上,
∴,
∵,
∴,
∴,
∴,
∴.
(2)解:∵将沿翻折,C点的对应点为G、点G落在矩形的内部,
∴,,
∵四边形是矩形,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
如图1,过作,连接交于点N,
∴四边形是矩形,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∵,
∴.
(3)解:如图2,作于,
由(1)知,,
∴是的平分线,
∵,
∴,
∵,,
∴,
∴,
设,则,,
由勾股定理得,,即,整理得,,
解得,,
∴.
(1)由矩形的性质可得,由翻折的性质可得,再利用垂直的定义、角平分线的定义、同角的余角相等可得,即,最后根据等角对等边即得结论;
(2)根据AAS证明,可得,过作,连接交于点N, 可得先证明可得,,再证明可得,最后根据线段的和差即可解答;
(3)如图2,作于,由(1)知,则是的平分线,则,根据HL证明,则,设,则,,由勾股定理得,即,解出x值,即得AG的长.
(1)解:∵四边形是矩形,
∴,
∴,
∵将沿翻折,C点的对应点为G、点G正好落在上,
∴,
∵,
∴,
∴,
∴,
∴.
(2)解:∵将沿翻折,C点的对应点为G、点G落在矩形的内部,
∴,,
∵四边形是矩形,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
如图1,过作,连接交于点N,
∴四边形是矩形,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∵,
∴.
(3)解:如图2,作于,
由(1)知,,
∴是的平分线,
∵,
∴,
∵,,
∴,
∴,
设,则,,
由勾股定理得,,即,整理得,,
解得,,
∴.
24.(1)解:①抛物线经过原点,,
对称轴为直线,
当时,,
抛物线的顶点,
设抛物线的解析式为,把代入,得,
解得:,
,
该抛物线的函数表达式为;
②设直线的解析式为,把代入,得:,
直线的解析式为,
直线与轴,轴分别交于点,,
,,
如图,过点作轴交于点,则点的纵坐标与点的纵坐标相同,
,解得:,
,
,
,
,
,
的值为.
(2)能相等,点的横坐标为6或或或.
解:(2)设点的横坐标为,
①如图2-1,当,存在,
图2-1
设,,则,
,
,
,
,
过点作轴于点,则,
在中,,
,
.
②如图2-2中,当时,存在.
图2-2
过点作轴于点,
同法,
,
.
图
③如图2-3中,当时,存在,
图2-3
,
,
,
,
,
同法,
,
.
④当时,同法,
,
图2-4
综上所述:点的横坐标为6或或或.
(1)①根据抛物线经过原点O(0,0)、C(2,0),可得抛物线的对称轴为直线,把x=1代入得顶点,设抛物线的解析式为,利用待定系数法把C(2,0)代入可得抛物线的函数表达式为.
②设直线的解析式为,运用待定系数法可得直线OP的解析式为,再由直线求出A(-2,0),B(0,),过点B作BF∥x轴交OP于点F,求得,可得,再由BF∥OC,得出△BEF∽△CEO,进而可得.
( 2 )分四种情形:①,②,③,④,分别作出图形求解即可.
25.(1)
(2)解:如图所示,
∵,,
∴,
∴
∴,
∴,
∵,,
∴;
(3)解:如图所示,过点作于点,
∵,,
∴,
则四边形是矩形,
∴
又∵
∴,
∴
∴
∴是等腰直角三角形;
(4)或或
解:(1) 如图所示,连接 ,
∵四边形 是矩形
∴
∵ ,
∴四边形 是矩形,
当点 和点 重合时,
∴ ,
在 中, ,
故答案为: .
(4) ①如图所示,当点 在 上时,
∵ ,
在 中, ,
则 ,
∵ ,则 , ,
在 中, ,
∴
解得:
当 时,点 在矩形内部,符合题意,
∴ 符合题意,
②当 点在 上时,当 重合时符合题意,此时如图,
则 , ,
在 中,
,
解得: ,
③当点 在 上,当 重合时,此时 与点 重合,则 是正方形,此时
综上所述, 或 或 .
(1)连接 ,先根据矩形的判定与性质证明四边形 是矩形,进而得到当点 和点 重合时, , ,再运用勾股定理即可求解;
(2)先根据题意即可得到,进而运用相似三角形的判定与性质证明即可得到,再代入数值即可求解;
(3)过点作于点,先根据矩形的判定与性质证明四边形是矩形即可得到,进而得到,再运用三角形全等的判定与性质证明即可得到,从而即可求解;
(4)分类讨论: ①如图所示,当点 在 上时,②当 点在 上时,当 重合时符合题意,③当点 在 上,当 重合时,此时 与点 重合,则 是正方形,进而运用勾股定理结合正方形的性质即可求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2 0 2 5 年 上 海 市 中 考 一 模 猜 题 卷
数 学 试 卷
姓名 ________准考证号________ 考场号 ________ 座位号________
1.本场考试时间100分钟.试卷共4页,满分150分,答题纸共2页
2.作答前,请在答题纸指定位置填写姓名、报名号、座位号.并将核对后的条形码贴在答题纸指定位置
3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域,不得错位.在试卷上作答一律不得分
4.用2B铅笔作答选择题,用黑色字迹钢笔、水笔或圆珠笔作答非
一、选择题(每题4分,共24分)
1.下列关系不正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.函数的自变量x的取值范围是( )
A. B. C. D.
3.若关于的一元二次方程有两个不相等的实数根,则的最小整数值为( )
A. B.0 C.1 D.2
4.为了解某公司的收入水平,随机挑选五人的月工资进行抽样调查,月工资(单位:元)分别是3000,4000,5000,6000,50000,那么能够较好的反映他们收入平均水平的是( )
A.中位数 B.标准差 C.平均数 D.众数
5.如图,在矩形中,为边上一点,.将沿翻折得到,的延长线交边于点,过点作交于点,连接,分别交于点E,F.现有以下结论:
①连接,则垂直平分;
②四边形是菱形;
③;
④若,则;其中正确的结论有( )个.
A.1 B.2 C.3 D.4
6.在中,,,,点在内,分别以为圆心画,圆半径为1,圆半径为2,圆半径为3,圆与圆内切,圆与圆的关系是( )
A.内含 B.相交 C.外切 D.相离
二、填空题(每题4分,共48分)
7.的值为 .
8.已知 是方程组 的解, 则代数式
9.方程的根是 .
10.基础教育“双减”工作监测平台数据显示,截至9月22日,全国有108000所义务教育学校已填报课后服务信息,108000用科学记数法可表示为 .
11.为预防“新冠病毒”,学校对教室喷洒消毒液(含氯消毒剂)进行消杀,资料表明空气中氯含量不低于,才能有效杀灭新冠病毒.如图,喷洒消毒液时教室空气中的氯含量与时间成正比例,消毒液挥发时,与成反比例,则此次消杀的有效作用时间是 min.
12.如图,在边长为的菱形中,,是边上的动点,是边上的动点,且,连接,则的最小值是 .
13.一辆汽车在行驶过程中,其行驶路程(千米)与行驶时间(小时)之间的函数关系如图所示.当时,与之间的函数表达式为;当时,与之间的函数表达式为 .
14.掷一枚六个面分别标有1,2,3,4,5,6的正方形骰子,则向上一面的数不大于5的概率是 .
15.计算: .
16.从一口鱼塘里随机捞出10条鱼,在这些鱼身上做上记号,然后把鱼放回鱼池.过一段时间后,在同样的地方再捞出100条鱼,其中带有记号的鱼有2条,根据抽样调查的方法,估计整个鱼塘约有鱼 条.
17.如图,有一张平行四边形纸条 ABCD,AD=5cm,AB=2cm, ∠A=120°, 点E,F 分别在边 AD,BC上,DE=1cm. 现将四边形 CFED沿EF折叠,使点C,D 分别落在点C’,D '上.当点C’恰好落在边AD上时,线段 CF的长为 cm .在点F 从点B 运动到点C的过程中,若边与边AD交于点M, 则点M相应运动的路径长为 cm.
18. 定义为二次函数的特征数,下面给出特征数为的函数结论,其中正确的结论是 .(填写序号)
①当时,点一定在函数的图象上;
②当时,函数图象截x轴所得的线段长度大于;
③当时,函数在时,y随x的增大而增大;
④若抛物线的顶点与抛物线与x轴两交点组成的三角形为等腰直角三角形,则
三、简答题(共78分,其中第19-22题每题10分,第23、24题每题12分,第25题14分)
19.计算:
(1);
(2).
解方程组:
.
21.如图,一次函数的图象与反比例函数的图象交于,两点.
(1)求反比例函数和一次函数的表达式.
(2)求的面积.
(3)当时,直接写出x的取值范围.
22.如图,在矩形中,,为边上一点,,连接.动点从点同时出发,点以的速度沿向终点运动;点以的速度沿折线向终点运动.设点运动的时间为,在运动过程中,点,点经过的路线与线段围成的图形面积为.
(1) , ;
(2)求关于的函数解析式,并写出自变量的取值范围;
(3)当时,直接写出的值.
23.如图,在矩形中,E,F分别是边上的点,,将沿翻折,C点的对应点为G.
(1)如图(1),若点G正好落在上.求证:;
(2)如图(2),若点G落在矩形的内部,且,延长交于点H,求证:;
(3)在(1)的条件下,若,.请直接写出的长度.
24. 如图1,直线与轴,轴分别交于点,,抛物线的顶点在直线上,与轴的交点为,,其中点的坐标为,直线与直线相交于点.
图1 图2 备用图
(1)如图2,若抛物线经过原点.
①求该抛物线的函数表达式;
②求的值;
抛物线的顶点在直线上运动的过程中,请问与能否相等?若能,请直接写出符合条件的点的横坐标;若不能,试说明理由.
25.如图①.在矩形.,点在边上,且.动点从点出发,沿折线以每秒个单位长度的速度运动,作,交边或边于点,连续.当点与点重合时,点停止运动.设点的运动时间为秒.()
(1)当点和点重合时,线段的长为 ;
(2)当点和点重合时,求;
(3)当点在边上运动时,的形状始终是等腰直角三角形.如图②.请说明理由;
(4)作点关于直线的对称点,连接、,当四边形和矩形重叠部分图形为轴对称四边形时,直接写出的取值范围.
答案解析部分
1.D
2.D
解:由题意可知,,
解得:,
故答案为:D.
利用二次根式有意义的条件(被开方数大于等于0)列出不等式求解即可.
3.D
4.A
5.C
6.B
解:如图,
∵ 圆与圆内切, 圆半径为1,圆半径为3,
∴ AP1=3-1=2
∴ BP1=AB-AP1=3
∵ AC=3,
∴ CP2=AC-AP2=1
∴ BP2=
∴ 3<BP<
∵ rB=2
∴ rB+rP=5,rB-rP=1
∴1<BP<5
∴ 圆P与圆B相交
故答案为:B
本题考查圆与圆的位置关系,两圆相交, 圆心距小于两圆半径的和,而大于两圆半径的差的绝对值。根据两圆半径和圆心距,可判定圆与圆的位置关系:设两个圆的半径为R和r,圆心距为d。
(1)d>R+r 两圆外离; 两圆的圆心距离之和大于两圆的半径之和。(2)d=R+r 两圆外切; 两圆的圆心距离之和等于两圆的半径之和。(3)d=R-r 两圆内切; 两圆的圆心距离之和等于两圆的半径之差。(4)d
8.-14
解:∵ 是方程组 的解,
∴,两式相乘,得-14.
故答案为:-14.
根据方程组解的意义,将解代入,再将两式相乘,得到待求式子的值.
9.x=2
方程两边平方得:
∴,
∵
∴
∴不符合题意,故舍去
∴原方程的根为x=2
故答案为:x=2.
将方程两边平方得,再求解即可。
10.
解:108000=,
故答案为:.
利用科学记数法的定义:把一个数写成a×10n的形式(其中1≤a<10,n为整数),这种记数法称为科学记数法,其方法如下:①确定a,a是只有一位整数的数,②确定n,当原数的绝对值≥10时,n为正整数,n等于原数的整数位数减1;当原数的绝对值<1,n为负整数,n的绝对值等于原数中左起第一个非0数前0的个数(含整数位上的0),再分析求解即可.
11.
12.
13.
解:当时,当x=0.5时,y=30,
当时,设与之间的函数表达式为y=kx+b,
将点(0.5,30),(2,150)代入得,
解得,
∴,
故答案为:
运用待定系数法求一次函数结合题意即可求解。
14.
15.
解:
,
故答案为:.
根据向量的运算法则进行计算可得答案。
16.500
17.;
解:如图,当点C恰好落在边AD上时,
∵四边形ABCD是平行四边形,且AD=5cm,AB=2cm, ∠A=120°, ∴CD=AB=2cm,∠D=60°,∠BCD=120°,AD∥BC,
∴∠CFE=∠C'EF,
由折叠性质得C'D'=CD=2cm,DE=D'E=1cm,∠D=∠D'=60°,∠CFE=∠C'FE,CF=C'F,
∴∠C'FE=∠C'EF,
∴C'E=C'F=CF,
过点E作EK⊥C'D'于点K,则∠EKD'=∠C'KE=90°,
∴∠KED'=30°,KD'=ED'=cm,
∴,C'K=C'D'-KD'=cm,
∴C'E=,
∴CF=cm;
当点F与点B重合时,AM最短,如图,
∵C'E=cm,C'D'=2cm,D'E=1cm,
∴D'E2+C'E2=4=D'C'2,
∴∠C'ED=90°,
∴∠EC'D'=30°,
∴∠MC'E=∠BC'D'-∠EC'D'=∠BCD-∠EC'D'=90°,
同前面可得BM=ME,设BM=ME=x,则C'M=BC'-BM=BC-BM=5-x,
在Rt△MC'E中,由勾股定理得ME2=C'E2+C'M2,即x2+3+(5-x)2,
解得x=,
∴AM=AD-DE-ME=;
当点C'在AD上时,此时M与点C'重合,如图,
由前面可得AM=AD-DE-C'E=4-cm,
∴点M的运动路程长为:4--=(2.8-)cm.
故答案为:2.8-.
当点C恰好落在边AD上时,易得CD=AB=2cm,∠D=60°,∠BCD=120°,AD∥BC,得∠CFE=∠C'EF,由折叠C'D'=CD=2cm,DE=D'E=1cm,∠D=∠D'=60°,∠CFE=∠C'FE,CF=C'F,则∠C'FE=∠C'EF,由等角对等边得C'E=C'F=CF,过点E作EK⊥C'D'于点K,则∠EKD'=∠C'KE=90°,根据含30°角直角三角形的性质及勾股定理可算出EK的长,进而由线段的和差可得C'K的长,再根据勾股定理算出C'E的长,从而即可求出CF的长;当点F与点B重合时,AM最短,如图,由勾股定理的逆定理判断出∠C'ED=90°,由三角形的内角和定理得∠EC'D'=30°,由角的和差得∠MC'E=90°,同前面可得BM=ME,设BM=ME=x,则C'M=BC'-BM=BC-BM=5-x,在Rt△MC'E中,由勾股定理建立方程可求出x的值,从而求出AM的长;当点C'在AD上时,此时M与点C'重合,如图,由前面可得AM的长,进而即可求出点M运动的路径长.
18.①②③
解:根据题意可得:二次函数解析式为,
当时,,
∴点一定在函数的图象上;
①正确;
当时,,
因式分解得
解得
函数图象截x轴所得的线段长度
②正确;
当时,
∴,抛物线开口向下,在对称轴右侧y随x的增大而减小,
对称轴为,
函数在时, 在对称轴左侧,y随x的增大而增大;
③正确;
④抛物线顶点的纵坐标为,
由②知抛物线与x轴两个交点坐标为解得,
∴两交点的距离为
∵抛物线的顶点与抛物线与x轴两交点组成的三角形为等腰直角三角形,
列方程得
解得,
经检验符合题意,是原方程的根,
④错误;
故答案为:①②③.
利用函数特征数可得二次函数解析式为,当时,把代入函数,求得可判断①,当时,,求出作差可判断②;当时, ,抛物线开口向下,在对称轴右侧y随x的增大而减小,对称轴为可判断③;若抛物线的顶点与抛物线与x轴两交点组成的三角形为等腰直角三角形,根据两交点关于对称轴对称构造方程,解得,可判断④.
19.(1)解:
;
(2)解:
.
(1)根据负整数指数幂运算法则、零指数幂运算法则及有理数的乘方运算法则分别计算,进而计算有理数的加减法运算即可;
(2)根据多项式除以单项式运算法则(多项式除以单项式,用多项式的每一项分别去除以单项式,再把所得的商相加)进行计算即可.
20.解:,
由得:代入中得:
,
,
,
,
解得:或,
当时,,
当时,,
∴方程组的解为或者.
本题考查解二元二次方程组,根据方程组的特点,用代入法求解比较简便。
21.(1)解:将A(-2,1)代入 得.
∴反比例函数的解析式为.
当x=1时,y2=-2, 即B坐标为.
将A,B两点坐标代入一次函数得,
,解得.
∴一次函数解析式为.
(2)解:设直线与x轴的交于M.
当时,,解得,即M.
∴.
(3)或
解:(3)当时,一次函数图象在反比例函数图象的上方,由图象可知,对应图象在A点左侧,即,或者O点和B点之间,即,
∴当时,x的取值范围是:或.
(1)先利用A点坐标求得反比例函数解析式,再求得B的坐标,利用待定系数法,将A、B代入求得一次函数的解析式;
(2)先求出直线与x轴的交点M,由进行计算即可;
(3)当时,一次函数图象在反比例函数图象的上方,结合函数图象即可得到x范围.
(1)解:将A点坐标代入反比例函数得,.
∴反比例函数的解析式为.
将B点坐标代入反比例函数解析式得,.
即点B的坐标为.
将A,B两点坐标代入一次函数解析式得,
,解得.
∴一次函数解析式为.
(2)令直线与x轴的交点为M.
将代入一次函数解析式得,,解得
即点M的坐标为.
∴,,
故.
(3)由函数图象可知,
在直线的左侧和直线与直线之间的部分,
一次函数的图象在反比例函数图象的上方,即,
∴当时,x的取值范围是:或.
22.(1);45°
(2)①当0<x≤2时,如图,过点P作PF⊥AD于点F,
∵cm,cm,
∴cm,
∴,
∴;
②当2<x≤3时,如图,过点P作PF⊥AD于点F,连接PD,
∵cm,cm,
∴
,
即;
③当3<x≤时,如图,点P与点E重合,
∵cm,cm,
∴
,
即,
综上:;
(3)解:或.
解:(1)∵AB=3,BE=AB=3
∴
∴
故答案为:第1空、
第2空、45°
(3)①当0<x≤2时,如图,
∵cm,cm,
∴cm,
当cm时,,解得;
②当2<x≤3时,如图,过点P作PM⊥CD于点M,过点P作于点F,
∵四边形MPFD是矩形,
∴cm,cm,cm,
∵,
∴,解得,
∵,
∴没有在范围内的x的值;
③当3<x≤时,如图,
∵cm,cm,,
∴,解得,(舍去),
∴,
综上:或.
(1)根据勾股定理可求出AE长,再根据等腰直角三角形性质可求出∠EAD的度数.
(2)分三种情况,画出图象,根据点的运动速度用x表示线段长度,由面积和差关系即可求出答案.
(3)分三种情况,画出图象,根据点的运动速度用x表示线段长度,根据勾股定理列出方程,解方程即可求出答案.
23.(1)解:∵四边形是矩形,
∴,
∴,
∵将沿翻折,C点的对应点为G、点G正好落在上,
∴,
∵,
∴,
∴,
∴,
∴.
(2)解:∵将沿翻折,C点的对应点为G、点G落在矩形的内部,
∴,,
∵四边形是矩形,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
如图1,过作,连接交于点N,
∴四边形是矩形,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∵,
∴.
(3)解:如图2,作于,
由(1)知,,
∴是的平分线,
∵,
∴,
∵,,
∴,
∴,
设,则,,
由勾股定理得,,即,整理得,,
解得,,
∴.
(1)由矩形的性质可得,由翻折的性质可得,再利用垂直的定义、角平分线的定义、同角的余角相等可得,即,最后根据等角对等边即得结论;
(2)根据AAS证明,可得,过作,连接交于点N, 可得先证明可得,,再证明可得,最后根据线段的和差即可解答;
(3)如图2,作于,由(1)知,则是的平分线,则,根据HL证明,则,设,则,,由勾股定理得,即,解出x值,即得AG的长.
(1)解:∵四边形是矩形,
∴,
∴,
∵将沿翻折,C点的对应点为G、点G正好落在上,
∴,
∵,
∴,
∴,
∴,
∴.
(2)解:∵将沿翻折,C点的对应点为G、点G落在矩形的内部,
∴,,
∵四边形是矩形,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
如图1,过作,连接交于点N,
∴四边形是矩形,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∵,
∴.
(3)解:如图2,作于,
由(1)知,,
∴是的平分线,
∵,
∴,
∵,,
∴,
∴,
设,则,,
由勾股定理得,,即,整理得,,
解得,,
∴.
24.(1)解:①抛物线经过原点,,
对称轴为直线,
当时,,
抛物线的顶点,
设抛物线的解析式为,把代入,得,
解得:,
,
该抛物线的函数表达式为;
②设直线的解析式为,把代入,得:,
直线的解析式为,
直线与轴,轴分别交于点,,
,,
如图,过点作轴交于点,则点的纵坐标与点的纵坐标相同,
,解得:,
,
,
,
,
,
的值为.
(2)能相等,点的横坐标为6或或或.
解:(2)设点的横坐标为,
①如图2-1,当,存在,
图2-1
设,,则,
,
,
,
,
过点作轴于点,则,
在中,,
,
.
②如图2-2中,当时,存在.
图2-2
过点作轴于点,
同法,
,
.
图
③如图2-3中,当时,存在,
图2-3
,
,
,
,
,
同法,
,
.
④当时,同法,
,
图2-4
综上所述:点的横坐标为6或或或.
(1)①根据抛物线经过原点O(0,0)、C(2,0),可得抛物线的对称轴为直线,把x=1代入得顶点,设抛物线的解析式为,利用待定系数法把C(2,0)代入可得抛物线的函数表达式为.
②设直线的解析式为,运用待定系数法可得直线OP的解析式为,再由直线求出A(-2,0),B(0,),过点B作BF∥x轴交OP于点F,求得,可得,再由BF∥OC,得出△BEF∽△CEO,进而可得.
( 2 )分四种情形:①,②,③,④,分别作出图形求解即可.
25.(1)
(2)解:如图所示,
∵,,
∴,
∴
∴,
∴,
∵,,
∴;
(3)解:如图所示,过点作于点,
∵,,
∴,
则四边形是矩形,
∴
又∵
∴,
∴
∴
∴是等腰直角三角形;
(4)或或
解:(1) 如图所示,连接 ,
∵四边形 是矩形
∴
∵ ,
∴四边形 是矩形,
当点 和点 重合时,
∴ ,
在 中, ,
故答案为: .
(4) ①如图所示,当点 在 上时,
∵ ,
在 中, ,
则 ,
∵ ,则 , ,
在 中, ,
∴
解得:
当 时,点 在矩形内部,符合题意,
∴ 符合题意,
②当 点在 上时,当 重合时符合题意,此时如图,
则 , ,
在 中,
,
解得: ,
③当点 在 上,当 重合时,此时 与点 重合,则 是正方形,此时
综上所述, 或 或 .
(1)连接 ,先根据矩形的判定与性质证明四边形 是矩形,进而得到当点 和点 重合时, , ,再运用勾股定理即可求解;
(2)先根据题意即可得到,进而运用相似三角形的判定与性质证明即可得到,再代入数值即可求解;
(3)过点作于点,先根据矩形的判定与性质证明四边形是矩形即可得到,进而得到,再运用三角形全等的判定与性质证明即可得到,从而即可求解;
(4)分类讨论: ①如图所示,当点 在 上时,②当 点在 上时,当 重合时符合题意,③当点 在 上,当 重合时,此时 与点 重合,则 是正方形,进而运用勾股定理结合正方形的性质即可求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
