2025年中考数学一模猜题卷(深圳专用)—2025年全国各地市最新中考数学模拟考试(含答案)
文档属性
| 名称 | 2025年中考数学一模猜题卷(深圳专用)—2025年全国各地市最新中考数学模拟考试(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 21:04:26 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
机密★启用前
2025 年 深 圳 市 中 考 一 模 猜 题 卷
数 学
说明:1 .答题前,请将姓名、准考证号和学校用黑色字迹的钢笔或签字笔填写在答题卡定 的位置上,并将条形码粘贴好。
2 .全卷共 6 页。考试时间 90 分钟,满分 100 分。
3 .作答选择题 1-8,选出每题答案后,用 2B 铅笔把答题卡上对应题目答案标号的 信息点框涂黑。如需改动,用橡皮擦干净后,再选涂其它答案。作答非选择题 9 -
20 ,用黑色字迹的钢笔或签字笔将答案(含作辅助线)写在答题卡指定区域内。写在 本试卷或草稿纸上,其答案一律无效。
4 .考试结束后,请将答题卡交回。
第一部分 选择题
一、选择题(本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 下列四个数中,最小的数是( )
A. B.0 C. D.2
2.芯片是半导体元件产品的统称,是一种将电路小型化的技术,常制造在半导体晶圆表面上.下列关于芯片的图标中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.下列计算正确的是( )
A. B. C. D.
4.根据分式的基本性质对分式变形,下列一定正确的是( )
A. B.
C. D.
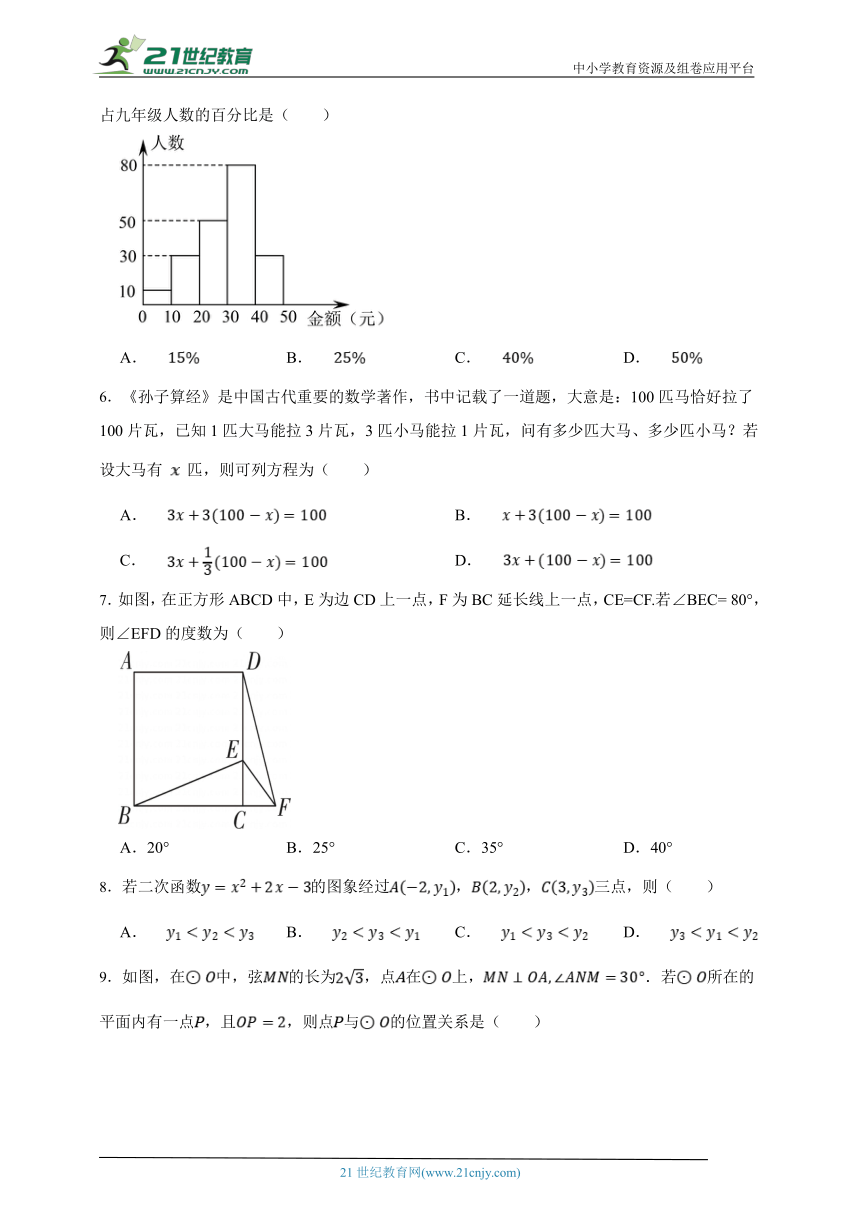
5.已知某校九年级200名学生义卖所得金额分布直方图如图所示,那么金额在20~30元的人数占九年级人数的百分比是( )
A. B. C. D.
6.《孙子算经》是中国古代重要的数学著作,书中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有 匹,则可列方程为( )
A. B.
C. D.
7.如图,在正方形ABCD中,E为边CD上一点,F为BC延长线上一点,CE=CF.若∠BEC= 80°,则∠EFD的度数为( )
A.20° B.25° C.35° D.40°
8.若二次函数的图象经过,,三点,则( )
A. B. C. D.
9.如图,在中,弦的长为,点在上,.若所在的平面内有一点,且,则点与的位置关系是( )
A.点在上 B.点在内 C.点在外 D.无法确定
10. 已知一个圆锥的底面半径为2,母线长为10,则这个圆锥的侧面积为( )
A. B. C. D.40
非选择题
二、填空题(本大题共6小题,每小题3分,满分18分.)
11.如图,,交于点E,若,则 .
12.若a=3+,b=3-,则a3b-ab3= .
13.如图,中,,点在的延长线上,,若平分,则 .
14.若a,b互为相反数,c,d互为倒数,且b≠0,则的值为
15.当 时, 代数式 与 的值相等.
16.如图,过原点的直线交反比例函数图象于,两点,过点分别作轴,轴的垂线,交反比例函数()的图象于,两点.若,则图中阴影部分的面积为 .
三、解答题(本大题共9小题,满分72分.解答应写出文字说明、证明过程或演算步骤.)
17.解分式方程:.
18.点是正方形的对角线上一点,过点作交于点,的延长线交于点,交于点.
(1)如图1,证明:;
(2)如图2,若,,求CF的长.
19.
(1)【尝试】如图,把一个等腰直角沿斜边上的中线(裁剪线)剪一刀,把分割成的两部分拼成一个四边形,如示意图1.(以下有画图要求的,工具不限,不必写画法和证明)
①猜一猜:四边形一定是 ;
②试一试:按上述的裁剪方法,请你拼一个与图1不同的四边形,并在图2中画出示意图.
(2)【探究】在等腰直角中,请你沿一条中位线(裁剪线)剪一刀,把分割成的两部分拼成一个四边形.
①想一想:你能拼得四边形分别是 (写出两种即可);
②画一画:请分别在图3,图4中画出你拼得的这两个四边形的示意图.
20.求下列各数的绝对值和相反数.
(1)
(2)
(3)3-π.
(4)
21.先在纸上写第一组数据:,,.如图,现有四张规格、质地完全相同的卡片,正面分别写有数字,,,,背面相同,将这四张卡片背面朝上洗匀,随机抽取若干张,把抽到卡片上的数字与第一组数据合在一起,得到第二组数据.将第二组数据与第一组数据进行比较.
(1)若随机抽取一张,求中位数不变的概率;
(2)若随机同时抽取两张,请用画树状图法或列表法,求众数不变的概率.
22.在“综合与实践”活动课上,活动小组测量一棵长在斜坡上的杨树的高度.如图,已知斜坡的坡度为米,在距离点C4米处的点D测得杨树顶端A的仰角为.
(1)______度;
(2)求杨树的高度.(,,在同一平面内,点C,D在同一水平线上,结果精确到米,参考数据:)
23.已知反比例函数在其图象所在的各象限内,随的增大而减小.
(1)求的最小整数值.
(2)判断直线与该反比例函数图象是否有交点,并说明理由.
24.如图,AB是的直径,弦,垂足为H,E为BC上一点,过点E作的切线,分别交DC,AB的延长线于点F,G.连接AE,交CD于点P.
(1)求证:;
(2)连接AD,若,,,求EG的长.
25.已知二次函数的图象对称轴为,图象交x轴于A、B两点,交y轴于,且,直线与二次函数图象交于M、N(M在N的右边),交y轴于P.
(1)求二次函数图象的解析式;
(2)若,若M、N均在第一象限,且的面积为3,求k的值;
(3)若,且M在第四象限,若直线交y轴于Q,求取值范围.
答案解析部分
1.A
解:-3<-1<0<2,
故答案为:A.
有理数比较大小,负数<0<正数;负数比较大小,绝对值大的反而小.
2.A
解:A、此选项中的图形既是轴对称图形又是中心对称图形,故符合题意;
B、此选项中的图形是轴对称图形,但不是中心对称图形,故不符合题意;
C、此选项中的图形既不是轴对称图形,也不是中心对称图形,故不符合题意;
D、此选项中的图形既不是轴对称图形,也不是中心对称图形,故不符合题意.
故答案为:A.
把一个图形绕某一点旋转180°后,能够与原图形重合,那么这个图形就叫做中心对称图形,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,据此逐一判断得出答案.
3.B
4.D
解:A选项:对于分式,分子分母同时加上同一个数,分式不一定成立,故A选项错误;
B选项:,故B选项错误;
C选项:,故C选项错误;
D选项:对于分式 ,分子分母同时乘同一个不为零的数,分式一定成立,故D选项正确.
故答案为:D.
根据分式的基本性质逐项分析,即可得到答案.
5.B
6.C
解:设大马有 x 匹,则由题意可得:
,
故答案为:C.
根据“大马拉瓦+小马拉瓦=100”可以列出方程 .
7.C
解:∵ 四边形ABCD为正方形,
∴ BC=DC,∠BCE=∠DCF=90°,
∵ CE=CF,
∴ △BCE≌△DCF(SAS),
∴ ∠BEC=∠DFC=80°,
∵ CE=CF,∠DCF=90°,
∴ ∠EFC=45°,
∴ ∠EFD=∠DFC-∠EFC=80°-45°=35°.
故答案为:C.
根据正方形的性质可得BC=DC,∠BCE=∠DCF=90°,依据SAS证明△BCE≌△DCF,得到∠BEC=∠DFC=80°,再根据等腰直角三角形的性质可得∠EFC=45°,最后根据∠EFD=∠DFC-∠EFC即可求得.
8.A
解:∵二次函数,
∴a=1>0,即二次函数图象的开口向上,对称轴是直线,
∵,, ,
∴点A、B、C与对称轴的距离分别为1、3、4,
∴,
故答案为:A
根据二次函数的解析式得出图象的开口向上,对称轴是直线,然后由在开口向上的二次函数中,二次函数上的点离对称轴越远,则对应的函数值约大,点离对称轴越近,则对应的函数值越小,据此即可求解.
9.A
10.A
解:根据题意可得:S侧面积=×l母×r底=,
故答案为:A.
利用圆锥侧面积公式列出算式求解即可.
11.
解:∵,,
,
;
故答案为:.
由两直线平行,同位角相等得∠DEF=∠A=42°,再利用邻补角的性质可得答案.
12.48
解:原式=ab(a2-b2)=ab(a+b)(a-b),把a、b分别代入得,原式=( 3+ )( 3- )( 3+ + 3- )( 3+ - 3+ )= 48 。
对原式进行化简,提取公因式ab,在把a、b分别带入进行计算即可。
13.5
解:在中,,
,,
,
平分,
,
,
,
,
故答案为:5.
由平行四边形的性质可知,,,继而可得,再由等角对等边的性质,得到,即可求出的长.
14.0
解:a,b互为相反数,c,d互为倒数,且b≠0,
=0+1+(-1)
=0.
故答案为:0.
根据相反数,倒数的性质可得,再整体代入代数式,化简即可求出答案.
15.
解:根据题意,我们有:,
移项,得到:,
化简,得到:,
即,
解出x的值,得到:,
故答案为:.
根据题意,我们可以得到,我们可以通过解这个方程来找到答案.
16.14
如图,连接OA,OB,延长AP交x轴于点C,
,,
,
P,Q关于原点中心对称,
,
同理可得,
.
故答案为:14.
连接OA,OB,延长AP交x轴于点C,得到,再由P,Q关于原点中心对称以及等底同高的三角形面积相等,得到,,即可推出图中阴影部分的面积.
17.解:
去分母得,3+2(x-1)=x,
解得,x=-1,
经检验,x=-1是原方程的解.
所以,原方程的解为:x=-1.
分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
18.(1)证明:如图,连接CE,
四边形是正方形,
∴对角线AC、BD互相垂直平分,CD=AD,∠ADF=90°,
∴CE=AE,
在和中,
,
∴,
∴∠ECD=∠EAD,
∵EF⊥AE,
∴∠AEF=90°,
∴∠AEF+∠ADF=180°,
,
又∵,
∴,
∴∠EFC=∠ECD,
∴CE=EF,
∴AE=EF;
(2)解:∵四边形是正方形,AB=2,
∴AB=AD=2,∠ABE=∠EDF=45°,∠BAD=90°,是等腰直角三角形,
∴,
设∠BAE=α,
∴∠EAD=∠BAD-∠BAE=90°-α,
∵AD=DE,
∴AB=AD=DE=2,∠AED=∠EAD=90°-α,
∵EF⊥AE,
∴∠AEF=90°,
∴∠DEF=∠AEF-∠AED=90°-90°+α=α,
∴∠DEF=∠BAE,
在和中,
,
∴,
∴,
∴.
(1)连接CE,根据正方形的性质得CD=AD,∠ADF=90°,CE=AE,然后证出,根据全等三角形对应角相等得∠ECD=∠EAD,接下来证出∠EFC=∠EAD,从而得∠EFC=∠ECD,进而根据“等角对等边”得CE=EF,即可得证结论;
(2)利用正方形的性质得AB=AD=2,∠ABE=∠EDF=45°,∠BAD=90°,是等腰直角三角形,根据等腰直角三角形的性质得,设∠BAE=α,则∠EAD=90°-α,然后利用等腰三角形“等边对等角”性质得∠AED=∠EAD=90°-α,从而证出∠DEF=∠BAE,接下来证出,根据全等三角形对应边相等得DF=BE的值,即可求出CF=CD-DF的值.
(1)证明:如图,连接.
四边形是正方形,
点,关于对称,
,.
,
,
又,
,
,
;
(2)由四边形是正方形,
得,,.
由,
得,,
得,即,
得,
得,
得.
19.(1)解:①平行四边形 ②如图2,将绕顺时针旋转至,则四边形是正方形;
(2)解:①平行四边形,矩形 ②如图3,为的中位线,拼四边形,由题意知,四边形是矩形; 如图4,为的中位线,拼四边形,由题意知,四边形是平行四边形;
解:(1)①由题意得∠DCB=∠A1=45°,∠A1BC=45°+90°=∠A1CD,
∴四边形一定是平行四边形,
故答案为:平行四边形
(1)①根据平行四边形的判定结合题意即可求解;②根据旋转的性质结合正方形的判定即可求解;
(2)根据矩形的判定结合三角形中位线定理即可求解。
20.(1)解:的绝对值是,相反数是
(2)解:的绝对值是,相反数是-
(3)解:3-π的绝对值是π-3,相反数是π-3
(4)解:的绝对值是-1,相反数是-1
(1)根据互为相反数的两个数和为0,和绝对值定义即可求解;
(2)根据互为相反数的两个数和为0,和绝对值定义即可求解;
(3)根据互为相反数的两个数和为0,和绝对值定义即可求解;
(4)根据互为相反数的两个数和为0,和绝对值定义即可求解.
21.(1)
(2)
22.(1)
(2)解:过点作的垂线,交于点,如下图:
,即,
解得:,
,即,
解得:,
在中,
,即,
,
解得:(米),
答:杨树的高度为米.
(1)解:斜坡的坡度为,
,
,
故答案为:;
(1)根据坡度得出,结合特殊角的三角函数值即可求出答案.
(2)过点作的垂线,交于点,根据锐角三角函数定义可得,,在中,结合特殊角的三角函数值及锐角三角函数定义建立方程,解方程即可求出答案.
(1)解:斜坡的坡度为,
,
,
故答案为:;
(2)解:过点作的垂线,交于点,如下图:
,即,
解得:,
,即,
解得:,
在中,
,即,
,
解得:(米),
答:杨树的高度为米.
23.(1)解:k的取值范围是k>-1,则k的最小整数值为0
(2)解:有交点,理由如下:
∵k+1>0,
∴反比例函数的图象在第一、三象限;
∵2>0,
∴直线y=2x经过原点,经过第一、三象限,
∴ 直线与该反比例函数图象有交点
(1)根据反比例函数的增减性质可知k+1>0,解不等式即可;
(2)根据反比例函数图象和正比例函数图象经过的象限进行判定即可。
24.(1)证明:连接,
为的切线,
,
,
在中,
又,
,
,
,
.
(2)解:,
,
,
,
,
,
在中,,
如图所示,连接,
设半径,则,
在中,,
,
解得,
在中,,
∴在中,,且,
,
.
(1)连接,先根据切线的性质得到,进而得到,再结合题意得到,从而根据等腰三角形的性质得到,再进行等量代换即可求解;
(2)根据平行线的性质得到,进而根据余弦函数的定义得到,再根据垂径定理得到,从而根据余弦函数求出AD,运用勾股定理求出AH,连接,设半径,则,根据勾股定理即可求出r,进而解直角三角形即可求出OG,从而运用勾股定理即可求出GE.
25.(1)解:设点,,则点,
则图象对称轴为,
解得,
故点A、B的坐标分别为,点,
则抛物线的表达式为,
∵抛物线交y轴于,
∴,
解得,
故抛物线的表达式为
(2)解:当m=5时,直线②,
设它交 y 轴于点 P,则,
∴,
则,
即③,
联立①②,整理得:,
则④,⑤,
联立③④⑤并解得或3(舍去3),
即
(3)解:当时,直线⑥,则直线过定点,
∵,
∴直线必过点B,
又∵M在第四象限,
∴点N与B重合,
即直线与x轴重合,
∴Q与原点O重合,
∵与y轴的交点P,
∴,
∵点,
∴,
而,
故,
联立①⑥并整理得:,
而,
解得,
∵M在B点右侧,
∴,
∴,
即.
本题考查二次函数的图象与性质,一元二次方程的根与系数的关系,一次函数的图象与性质.
(1)设点,根据可知点,根据对称轴可求出对称轴为:,据此可得点A、B的坐标分别为,点,可设抛物线的表达式为,再把代入表达式,可列出方程,解方程可求出a值,进而可求出抛物线的表达式;
(2)易求②,进而可求出交 y 轴于点,求出,根据,利用三角形的面积计算公式可推出③,联立①②,整理得:,利用一元二次方程根与系数的关系可得:④,⑤,联立③④⑤可求出k的值;
(3)当时,则⑥,据此可推出直线过定点,再证明点N与B重合,Q与原点O重合,根据点,点,可求出,,即有,联立①⑥并整理得:,利用一元二次方程根与系数的关系可得:,解得,进而可列出不等式,解不等式可得:,进而可求出答案.
(1)设点,,
则点,
则图象对称轴为,
解得,
故点A、B的坐标分别为,点,
则抛物线的表达式为,
∵抛物线交y轴于,
∴,
解得,
故抛物线的表达式为①;
(2)∵,
∴直线②,设它交 y 轴于点 P,则,
∴,
则,
即③,
联立①②,整理得:,
则④,⑤,
联立③④⑤并解得或3(舍去3),
即;
(3)当时,
则⑥,则直线过定点,
∵,
∴直线必过点B,
又∵M在第四象限,
∴点N与B重合,
即直线与x轴重合,
∴Q与原点O重合,
∵与y轴的交点P,
∴,
∵点,
∴,
而,
故,
联立①⑥并整理得:,
而,
解得,
∵M在B点右侧,
∴,
即,
即.
●
C
A
D
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
机密★启用前
2025 年 深 圳 市 中 考 一 模 猜 题 卷
数 学
说明:1 .答题前,请将姓名、准考证号和学校用黑色字迹的钢笔或签字笔填写在答题卡定 的位置上,并将条形码粘贴好。
2 .全卷共 6 页。考试时间 90 分钟,满分 100 分。
3 .作答选择题 1-8,选出每题答案后,用 2B 铅笔把答题卡上对应题目答案标号的 信息点框涂黑。如需改动,用橡皮擦干净后,再选涂其它答案。作答非选择题 9 -
20 ,用黑色字迹的钢笔或签字笔将答案(含作辅助线)写在答题卡指定区域内。写在 本试卷或草稿纸上,其答案一律无效。
4 .考试结束后,请将答题卡交回。
第一部分 选择题
一、选择题(本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 下列四个数中,最小的数是( )
A. B.0 C. D.2
2.芯片是半导体元件产品的统称,是一种将电路小型化的技术,常制造在半导体晶圆表面上.下列关于芯片的图标中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.下列计算正确的是( )
A. B. C. D.
4.根据分式的基本性质对分式变形,下列一定正确的是( )
A. B.
C. D.
5.已知某校九年级200名学生义卖所得金额分布直方图如图所示,那么金额在20~30元的人数占九年级人数的百分比是( )
A. B. C. D.
6.《孙子算经》是中国古代重要的数学著作,书中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有 匹,则可列方程为( )
A. B.
C. D.
7.如图,在正方形ABCD中,E为边CD上一点,F为BC延长线上一点,CE=CF.若∠BEC= 80°,则∠EFD的度数为( )
A.20° B.25° C.35° D.40°
8.若二次函数的图象经过,,三点,则( )
A. B. C. D.
9.如图,在中,弦的长为,点在上,.若所在的平面内有一点,且,则点与的位置关系是( )
A.点在上 B.点在内 C.点在外 D.无法确定
10. 已知一个圆锥的底面半径为2,母线长为10,则这个圆锥的侧面积为( )
A. B. C. D.40
非选择题
二、填空题(本大题共6小题,每小题3分,满分18分.)
11.如图,,交于点E,若,则 .
12.若a=3+,b=3-,则a3b-ab3= .
13.如图,中,,点在的延长线上,,若平分,则 .
14.若a,b互为相反数,c,d互为倒数,且b≠0,则的值为
15.当 时, 代数式 与 的值相等.
16.如图,过原点的直线交反比例函数图象于,两点,过点分别作轴,轴的垂线,交反比例函数()的图象于,两点.若,则图中阴影部分的面积为 .
三、解答题(本大题共9小题,满分72分.解答应写出文字说明、证明过程或演算步骤.)
17.解分式方程:.
18.点是正方形的对角线上一点,过点作交于点,的延长线交于点,交于点.
(1)如图1,证明:;
(2)如图2,若,,求CF的长.
19.
(1)【尝试】如图,把一个等腰直角沿斜边上的中线(裁剪线)剪一刀,把分割成的两部分拼成一个四边形,如示意图1.(以下有画图要求的,工具不限,不必写画法和证明)
①猜一猜:四边形一定是 ;
②试一试:按上述的裁剪方法,请你拼一个与图1不同的四边形,并在图2中画出示意图.
(2)【探究】在等腰直角中,请你沿一条中位线(裁剪线)剪一刀,把分割成的两部分拼成一个四边形.
①想一想:你能拼得四边形分别是 (写出两种即可);
②画一画:请分别在图3,图4中画出你拼得的这两个四边形的示意图.
20.求下列各数的绝对值和相反数.
(1)
(2)
(3)3-π.
(4)
21.先在纸上写第一组数据:,,.如图,现有四张规格、质地完全相同的卡片,正面分别写有数字,,,,背面相同,将这四张卡片背面朝上洗匀,随机抽取若干张,把抽到卡片上的数字与第一组数据合在一起,得到第二组数据.将第二组数据与第一组数据进行比较.
(1)若随机抽取一张,求中位数不变的概率;
(2)若随机同时抽取两张,请用画树状图法或列表法,求众数不变的概率.
22.在“综合与实践”活动课上,活动小组测量一棵长在斜坡上的杨树的高度.如图,已知斜坡的坡度为米,在距离点C4米处的点D测得杨树顶端A的仰角为.
(1)______度;
(2)求杨树的高度.(,,在同一平面内,点C,D在同一水平线上,结果精确到米,参考数据:)
23.已知反比例函数在其图象所在的各象限内,随的增大而减小.
(1)求的最小整数值.
(2)判断直线与该反比例函数图象是否有交点,并说明理由.
24.如图,AB是的直径,弦,垂足为H,E为BC上一点,过点E作的切线,分别交DC,AB的延长线于点F,G.连接AE,交CD于点P.
(1)求证:;
(2)连接AD,若,,,求EG的长.
25.已知二次函数的图象对称轴为,图象交x轴于A、B两点,交y轴于,且,直线与二次函数图象交于M、N(M在N的右边),交y轴于P.
(1)求二次函数图象的解析式;
(2)若,若M、N均在第一象限,且的面积为3,求k的值;
(3)若,且M在第四象限,若直线交y轴于Q,求取值范围.
答案解析部分
1.A
解:-3<-1<0<2,
故答案为:A.
有理数比较大小,负数<0<正数;负数比较大小,绝对值大的反而小.
2.A
解:A、此选项中的图形既是轴对称图形又是中心对称图形,故符合题意;
B、此选项中的图形是轴对称图形,但不是中心对称图形,故不符合题意;
C、此选项中的图形既不是轴对称图形,也不是中心对称图形,故不符合题意;
D、此选项中的图形既不是轴对称图形,也不是中心对称图形,故不符合题意.
故答案为:A.
把一个图形绕某一点旋转180°后,能够与原图形重合,那么这个图形就叫做中心对称图形,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,据此逐一判断得出答案.
3.B
4.D
解:A选项:对于分式,分子分母同时加上同一个数,分式不一定成立,故A选项错误;
B选项:,故B选项错误;
C选项:,故C选项错误;
D选项:对于分式 ,分子分母同时乘同一个不为零的数,分式一定成立,故D选项正确.
故答案为:D.
根据分式的基本性质逐项分析,即可得到答案.
5.B
6.C
解:设大马有 x 匹,则由题意可得:
,
故答案为:C.
根据“大马拉瓦+小马拉瓦=100”可以列出方程 .
7.C
解:∵ 四边形ABCD为正方形,
∴ BC=DC,∠BCE=∠DCF=90°,
∵ CE=CF,
∴ △BCE≌△DCF(SAS),
∴ ∠BEC=∠DFC=80°,
∵ CE=CF,∠DCF=90°,
∴ ∠EFC=45°,
∴ ∠EFD=∠DFC-∠EFC=80°-45°=35°.
故答案为:C.
根据正方形的性质可得BC=DC,∠BCE=∠DCF=90°,依据SAS证明△BCE≌△DCF,得到∠BEC=∠DFC=80°,再根据等腰直角三角形的性质可得∠EFC=45°,最后根据∠EFD=∠DFC-∠EFC即可求得.
8.A
解:∵二次函数,
∴a=1>0,即二次函数图象的开口向上,对称轴是直线,
∵,, ,
∴点A、B、C与对称轴的距离分别为1、3、4,
∴,
故答案为:A
根据二次函数的解析式得出图象的开口向上,对称轴是直线,然后由在开口向上的二次函数中,二次函数上的点离对称轴越远,则对应的函数值约大,点离对称轴越近,则对应的函数值越小,据此即可求解.
9.A
10.A
解:根据题意可得:S侧面积=×l母×r底=,
故答案为:A.
利用圆锥侧面积公式列出算式求解即可.
11.
解:∵,,
,
;
故答案为:.
由两直线平行,同位角相等得∠DEF=∠A=42°,再利用邻补角的性质可得答案.
12.48
解:原式=ab(a2-b2)=ab(a+b)(a-b),把a、b分别代入得,原式=( 3+ )( 3- )( 3+ + 3- )( 3+ - 3+ )= 48 。
对原式进行化简,提取公因式ab,在把a、b分别带入进行计算即可。
13.5
解:在中,,
,,
,
平分,
,
,
,
,
故答案为:5.
由平行四边形的性质可知,,,继而可得,再由等角对等边的性质,得到,即可求出的长.
14.0
解:a,b互为相反数,c,d互为倒数,且b≠0,
=0+1+(-1)
=0.
故答案为:0.
根据相反数,倒数的性质可得,再整体代入代数式,化简即可求出答案.
15.
解:根据题意,我们有:,
移项,得到:,
化简,得到:,
即,
解出x的值,得到:,
故答案为:.
根据题意,我们可以得到,我们可以通过解这个方程来找到答案.
16.14
如图,连接OA,OB,延长AP交x轴于点C,
,,
,
P,Q关于原点中心对称,
,
同理可得,
.
故答案为:14.
连接OA,OB,延长AP交x轴于点C,得到,再由P,Q关于原点中心对称以及等底同高的三角形面积相等,得到,,即可推出图中阴影部分的面积.
17.解:
去分母得,3+2(x-1)=x,
解得,x=-1,
经检验,x=-1是原方程的解.
所以,原方程的解为:x=-1.
分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
18.(1)证明:如图,连接CE,
四边形是正方形,
∴对角线AC、BD互相垂直平分,CD=AD,∠ADF=90°,
∴CE=AE,
在和中,
,
∴,
∴∠ECD=∠EAD,
∵EF⊥AE,
∴∠AEF=90°,
∴∠AEF+∠ADF=180°,
,
又∵,
∴,
∴∠EFC=∠ECD,
∴CE=EF,
∴AE=EF;
(2)解:∵四边形是正方形,AB=2,
∴AB=AD=2,∠ABE=∠EDF=45°,∠BAD=90°,是等腰直角三角形,
∴,
设∠BAE=α,
∴∠EAD=∠BAD-∠BAE=90°-α,
∵AD=DE,
∴AB=AD=DE=2,∠AED=∠EAD=90°-α,
∵EF⊥AE,
∴∠AEF=90°,
∴∠DEF=∠AEF-∠AED=90°-90°+α=α,
∴∠DEF=∠BAE,
在和中,
,
∴,
∴,
∴.
(1)连接CE,根据正方形的性质得CD=AD,∠ADF=90°,CE=AE,然后证出,根据全等三角形对应角相等得∠ECD=∠EAD,接下来证出∠EFC=∠EAD,从而得∠EFC=∠ECD,进而根据“等角对等边”得CE=EF,即可得证结论;
(2)利用正方形的性质得AB=AD=2,∠ABE=∠EDF=45°,∠BAD=90°,是等腰直角三角形,根据等腰直角三角形的性质得,设∠BAE=α,则∠EAD=90°-α,然后利用等腰三角形“等边对等角”性质得∠AED=∠EAD=90°-α,从而证出∠DEF=∠BAE,接下来证出,根据全等三角形对应边相等得DF=BE的值,即可求出CF=CD-DF的值.
(1)证明:如图,连接.
四边形是正方形,
点,关于对称,
,.
,
,
又,
,
,
;
(2)由四边形是正方形,
得,,.
由,
得,,
得,即,
得,
得,
得.
19.(1)解:①平行四边形 ②如图2,将绕顺时针旋转至,则四边形是正方形;
(2)解:①平行四边形,矩形 ②如图3,为的中位线,拼四边形,由题意知,四边形是矩形; 如图4,为的中位线,拼四边形,由题意知,四边形是平行四边形;
解:(1)①由题意得∠DCB=∠A1=45°,∠A1BC=45°+90°=∠A1CD,
∴四边形一定是平行四边形,
故答案为:平行四边形
(1)①根据平行四边形的判定结合题意即可求解;②根据旋转的性质结合正方形的判定即可求解;
(2)根据矩形的判定结合三角形中位线定理即可求解。
20.(1)解:的绝对值是,相反数是
(2)解:的绝对值是,相反数是-
(3)解:3-π的绝对值是π-3,相反数是π-3
(4)解:的绝对值是-1,相反数是-1
(1)根据互为相反数的两个数和为0,和绝对值定义即可求解;
(2)根据互为相反数的两个数和为0,和绝对值定义即可求解;
(3)根据互为相反数的两个数和为0,和绝对值定义即可求解;
(4)根据互为相反数的两个数和为0,和绝对值定义即可求解.
21.(1)
(2)
22.(1)
(2)解:过点作的垂线,交于点,如下图:
,即,
解得:,
,即,
解得:,
在中,
,即,
,
解得:(米),
答:杨树的高度为米.
(1)解:斜坡的坡度为,
,
,
故答案为:;
(1)根据坡度得出,结合特殊角的三角函数值即可求出答案.
(2)过点作的垂线,交于点,根据锐角三角函数定义可得,,在中,结合特殊角的三角函数值及锐角三角函数定义建立方程,解方程即可求出答案.
(1)解:斜坡的坡度为,
,
,
故答案为:;
(2)解:过点作的垂线,交于点,如下图:
,即,
解得:,
,即,
解得:,
在中,
,即,
,
解得:(米),
答:杨树的高度为米.
23.(1)解:k的取值范围是k>-1,则k的最小整数值为0
(2)解:有交点,理由如下:
∵k+1>0,
∴反比例函数的图象在第一、三象限;
∵2>0,
∴直线y=2x经过原点,经过第一、三象限,
∴ 直线与该反比例函数图象有交点
(1)根据反比例函数的增减性质可知k+1>0,解不等式即可;
(2)根据反比例函数图象和正比例函数图象经过的象限进行判定即可。
24.(1)证明:连接,
为的切线,
,
,
在中,
又,
,
,
,
.
(2)解:,
,
,
,
,
,
在中,,
如图所示,连接,
设半径,则,
在中,,
,
解得,
在中,,
∴在中,,且,
,
.
(1)连接,先根据切线的性质得到,进而得到,再结合题意得到,从而根据等腰三角形的性质得到,再进行等量代换即可求解;
(2)根据平行线的性质得到,进而根据余弦函数的定义得到,再根据垂径定理得到,从而根据余弦函数求出AD,运用勾股定理求出AH,连接,设半径,则,根据勾股定理即可求出r,进而解直角三角形即可求出OG,从而运用勾股定理即可求出GE.
25.(1)解:设点,,则点,
则图象对称轴为,
解得,
故点A、B的坐标分别为,点,
则抛物线的表达式为,
∵抛物线交y轴于,
∴,
解得,
故抛物线的表达式为
(2)解:当m=5时,直线②,
设它交 y 轴于点 P,则,
∴,
则,
即③,
联立①②,整理得:,
则④,⑤,
联立③④⑤并解得或3(舍去3),
即
(3)解:当时,直线⑥,则直线过定点,
∵,
∴直线必过点B,
又∵M在第四象限,
∴点N与B重合,
即直线与x轴重合,
∴Q与原点O重合,
∵与y轴的交点P,
∴,
∵点,
∴,
而,
故,
联立①⑥并整理得:,
而,
解得,
∵M在B点右侧,
∴,
∴,
即.
本题考查二次函数的图象与性质,一元二次方程的根与系数的关系,一次函数的图象与性质.
(1)设点,根据可知点,根据对称轴可求出对称轴为:,据此可得点A、B的坐标分别为,点,可设抛物线的表达式为,再把代入表达式,可列出方程,解方程可求出a值,进而可求出抛物线的表达式;
(2)易求②,进而可求出交 y 轴于点,求出,根据,利用三角形的面积计算公式可推出③,联立①②,整理得:,利用一元二次方程根与系数的关系可得:④,⑤,联立③④⑤可求出k的值;
(3)当时,则⑥,据此可推出直线过定点,再证明点N与B重合,Q与原点O重合,根据点,点,可求出,,即有,联立①⑥并整理得:,利用一元二次方程根与系数的关系可得:,解得,进而可列出不等式,解不等式可得:,进而可求出答案.
(1)设点,,
则点,
则图象对称轴为,
解得,
故点A、B的坐标分别为,点,
则抛物线的表达式为,
∵抛物线交y轴于,
∴,
解得,
故抛物线的表达式为①;
(2)∵,
∴直线②,设它交 y 轴于点 P,则,
∴,
则,
即③,
联立①②,整理得:,
则④,⑤,
联立③④⑤并解得或3(舍去3),
即;
(3)当时,
则⑥,则直线过定点,
∵,
∴直线必过点B,
又∵M在第四象限,
∴点N与B重合,
即直线与x轴重合,
∴Q与原点O重合,
∵与y轴的交点P,
∴,
∵点,
∴,
而,
故,
联立①⑥并整理得:,
而,
解得,
∵M在B点右侧,
∴,
即,
即.
●
C
A
D
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
