2024-2025学年江西省吉安市高一上学期期末教学质量检测数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年江西省吉安市高一上学期期末教学质量检测数学试卷(含答案) | 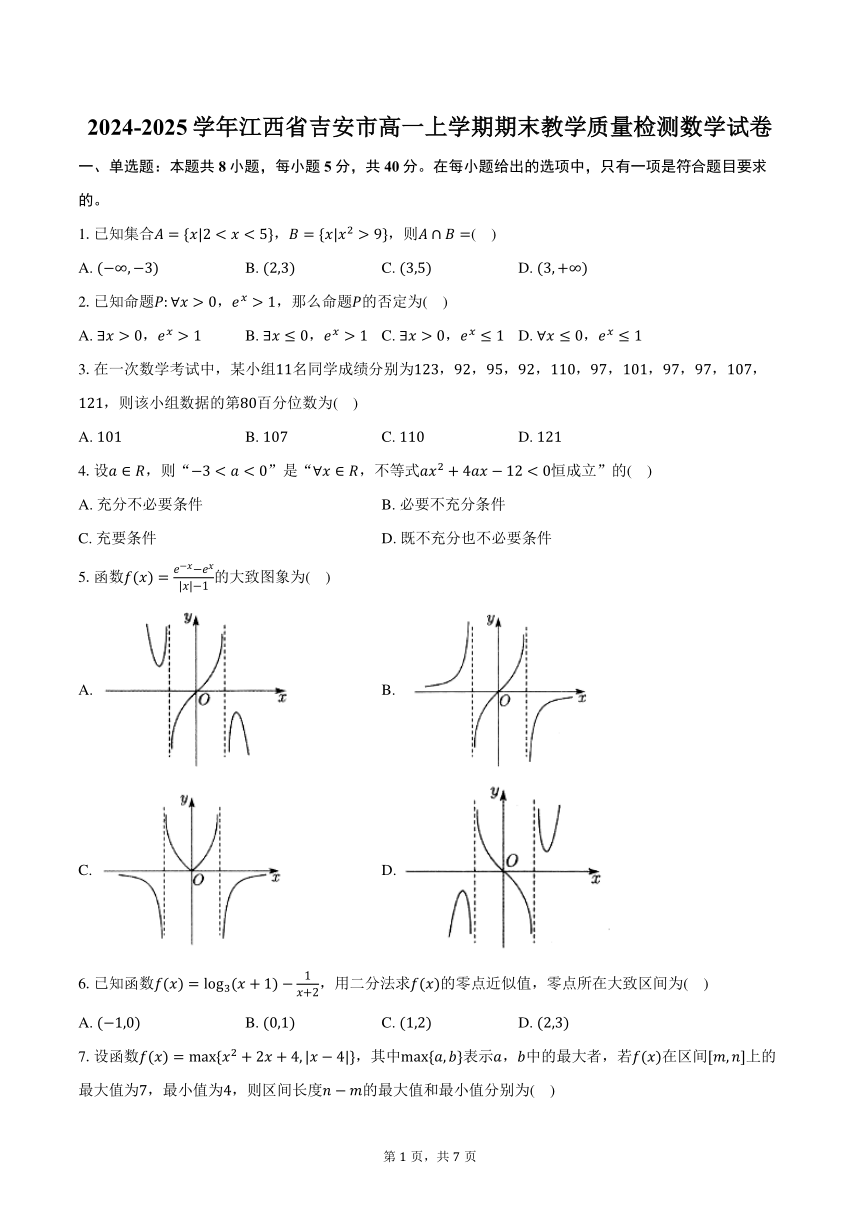 | |
| 格式 | docx | ||
| 文件大小 | 72.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 19:31:41 | ||
图片预览



文档简介
2024-2025学年江西省吉安市高一上学期期末教学质量检测数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.已知命题,,那么命题的否定为( )
A. , B. , C. , D. ,
3.在一次数学考试中,某小组名同学成绩分别为,,,,,,,,,,,则该小组数据的第百分位数为( )
A. B. C. D.
4.设,则“”是“,不等式恒成立”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5.函数的大致图象为( )
A. B.
C. D.
6.已知函数,用二分法求的零点近似值,零点所在大致区间为( )
A. B. C. D.
7.设函数,其中表示,中的最大者,若在区间上的最大值为,最小值为,则区间长度的最大值和最小值分别为( )
A. , B. , C. , D. ,
8.设,,若,则( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.对于实数,,,下列说法正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
10.井冈蜜柚以其皮薄核少、柚香浓郁、口感清甜的特点深受人们喜爱为了解某蜜柚种植园的产量情况,随机抽取了其中株蜜柚树,测量每株产量单位:,所得数据整理并绘制成如图所示的频率分布直方图,则下列说法正确的是( )
A. 图中的值为
B. 样本中单株蜜柚树的产量少于的树木有株
C. 估计该种植园中单株蜜柚树的产量众数为
D. 估计该种植园中单株蜜柚树的产量的平均数超过每组数据用该组所在区间的中点值作代表
11.若,是关于的方程的两根,且,,则下列说法正确的是( )
A. 的取值范围是 B. 的最大值为
C. 的最大值为 D. 的最小值为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知函数,则的定义域为 .
13.吉安,有“吉泰民安”之美誉,拥有丰富的历史文化底蕴和秀丽的自然风光小明准备在寒假期间前往吉安旅游,他计划用三天时间游览“武功山”、“钓源古村”、“后河梦回庐陵”这三个景点,一天只能游览一个景点,如果按照任意次序排出游览顺序表,则第一天游览“武功山”或“钓源古村”的概率为 .
14.若函数在区间有且仅有一个零点,则实数的取值范围是 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
计算:
.
16.本小题分
已知集合,.
若,求B.
若,求实数的取值范围.
17.本小题分
已知函数.
证明:函数的图象关于点中心对称.
解不等式:.
18.本小题分
地球表面的水储量大约有亿亿立方米,但淡水资源只有亿亿立方米,在有限的淡水资源中,仅有是人类可以利用的,水是人类赖以生存的宝贵资源,节约用水,利在当代,功在千秋为了提高居民节约用水的意识,某城市对居民采用“阶梯水价”的计费方式,其计价规则如下:
每户每月用水水量 水价
不超过的部分 元
超过但不超过的部分 元
超过的部分 元
写出用户居民每月所需要缴纳的水费单位:元与用水量单位:之间的函数关系.
某小区的物业公司为提高居民节约用水的积极性,将每月给缴纳水费不超过元的用户评定为“节水榜样用户”,被评为“节水榜样用户”的居民可参加物业举办的抽奖活动,抽奖规则如下:一个不透明的箱子中装有两个编号为,两个编号为,一个编号为的小球,这个小球除编号外其余均相同,用户从箱子中依次取出两个小球,若小球的编号之和为的倍数,则代表中奖,问:
“节水榜样用户”的月用水量不能超过多少
参加抽奖活动的“节水榜样用户”中奖的概率是多少
19.本小题分
函数,
记,求的取值范围.
记函数的最小值为,求.
求方程的解集.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.,且
13.
14.或
15.解:原式;
原式.
16.解:若,则,
,
当时,,此时,符合题意
当时,,要使,则有或,解得.
当时,,要使,则有或,解得
综上,的取值范围是.
17.解:函数的定义域为.
由,得函数的图象关于点中心对称.
函数在定义域上单调递增,
由知,函数的图象关于点中心对称,则有,
不等式
等价于,则有:
解得:.
18.解:依题,当时,
当时,
当时,.
综上:
由,得,
因此,月用水量不超过的用户可被评为“节水榜样用户”.
记两个编号为的小球为,,两个编号为的小球为,,编号为的小球为,
则该次抽奖活动的样本空间,,,,,,,,,,,,,,,,,,共个样本点.
其中中奖的情况有,,,,,,,共个,
因此,参加抽奖活动的“节水榜样用户”中奖的概率为
19.【解答】解:
,其中,则,因为,所以,所以,;
由得,所以,令,,
则有:当时,,;
当时,在上单调递增,则;
当时,是一个开口向下的二次函数,且对称轴,
此时;
当时,是一个开口向下的二次函数,且对称轴,
此时,
综上:;
当时,,此时解得;
当时,,若,即,
则,此时方程无解;
若,即时,,此时方程的解为,
综上,方程的解集为
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.已知命题,,那么命题的否定为( )
A. , B. , C. , D. ,
3.在一次数学考试中,某小组名同学成绩分别为,,,,,,,,,,,则该小组数据的第百分位数为( )
A. B. C. D.
4.设,则“”是“,不等式恒成立”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5.函数的大致图象为( )
A. B.
C. D.
6.已知函数,用二分法求的零点近似值,零点所在大致区间为( )
A. B. C. D.
7.设函数,其中表示,中的最大者,若在区间上的最大值为,最小值为,则区间长度的最大值和最小值分别为( )
A. , B. , C. , D. ,
8.设,,若,则( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.对于实数,,,下列说法正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
10.井冈蜜柚以其皮薄核少、柚香浓郁、口感清甜的特点深受人们喜爱为了解某蜜柚种植园的产量情况,随机抽取了其中株蜜柚树,测量每株产量单位:,所得数据整理并绘制成如图所示的频率分布直方图,则下列说法正确的是( )
A. 图中的值为
B. 样本中单株蜜柚树的产量少于的树木有株
C. 估计该种植园中单株蜜柚树的产量众数为
D. 估计该种植园中单株蜜柚树的产量的平均数超过每组数据用该组所在区间的中点值作代表
11.若,是关于的方程的两根,且,,则下列说法正确的是( )
A. 的取值范围是 B. 的最大值为
C. 的最大值为 D. 的最小值为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知函数,则的定义域为 .
13.吉安,有“吉泰民安”之美誉,拥有丰富的历史文化底蕴和秀丽的自然风光小明准备在寒假期间前往吉安旅游,他计划用三天时间游览“武功山”、“钓源古村”、“后河梦回庐陵”这三个景点,一天只能游览一个景点,如果按照任意次序排出游览顺序表,则第一天游览“武功山”或“钓源古村”的概率为 .
14.若函数在区间有且仅有一个零点,则实数的取值范围是 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
计算:
.
16.本小题分
已知集合,.
若,求B.
若,求实数的取值范围.
17.本小题分
已知函数.
证明:函数的图象关于点中心对称.
解不等式:.
18.本小题分
地球表面的水储量大约有亿亿立方米,但淡水资源只有亿亿立方米,在有限的淡水资源中,仅有是人类可以利用的,水是人类赖以生存的宝贵资源,节约用水,利在当代,功在千秋为了提高居民节约用水的意识,某城市对居民采用“阶梯水价”的计费方式,其计价规则如下:
每户每月用水水量 水价
不超过的部分 元
超过但不超过的部分 元
超过的部分 元
写出用户居民每月所需要缴纳的水费单位:元与用水量单位:之间的函数关系.
某小区的物业公司为提高居民节约用水的积极性,将每月给缴纳水费不超过元的用户评定为“节水榜样用户”,被评为“节水榜样用户”的居民可参加物业举办的抽奖活动,抽奖规则如下:一个不透明的箱子中装有两个编号为,两个编号为,一个编号为的小球,这个小球除编号外其余均相同,用户从箱子中依次取出两个小球,若小球的编号之和为的倍数,则代表中奖,问:
“节水榜样用户”的月用水量不能超过多少
参加抽奖活动的“节水榜样用户”中奖的概率是多少
19.本小题分
函数,
记,求的取值范围.
记函数的最小值为,求.
求方程的解集.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.,且
13.
14.或
15.解:原式;
原式.
16.解:若,则,
,
当时,,此时,符合题意
当时,,要使,则有或,解得.
当时,,要使,则有或,解得
综上,的取值范围是.
17.解:函数的定义域为.
由,得函数的图象关于点中心对称.
函数在定义域上单调递增,
由知,函数的图象关于点中心对称,则有,
不等式
等价于,则有:
解得:.
18.解:依题,当时,
当时,
当时,.
综上:
由,得,
因此,月用水量不超过的用户可被评为“节水榜样用户”.
记两个编号为的小球为,,两个编号为的小球为,,编号为的小球为,
则该次抽奖活动的样本空间,,,,,,,,,,,,,,,,,,共个样本点.
其中中奖的情况有,,,,,,,共个,
因此,参加抽奖活动的“节水榜样用户”中奖的概率为
19.【解答】解:
,其中,则,因为,所以,所以,;
由得,所以,令,,
则有:当时,,;
当时,在上单调递增,则;
当时,是一个开口向下的二次函数,且对称轴,
此时;
当时,是一个开口向下的二次函数,且对称轴,
此时,
综上:;
当时,,此时解得;
当时,,若,即,
则,此时方程无解;
若,即时,,此时方程的解为,
综上,方程的解集为
第1页,共1页
同课章节目录
